基于预测控制的多种新能源互补电力系统动态调度模型

2021-06-10周坤许云飞崔昊杨李树林

现代电力 2021年3期

周坤，许云飞，崔昊杨，李树林

（1. 大理供电局，云南省大理市 671000；2. 上海电力大学电子与信息工程学院，上海市杨浦区 200090）

0 引言

以风力、光伏、水力、垃圾发电为代表的分布式新能源，与能量转换装置、用户集中在一起组成的电力系统在建设绿色、环境友好型的发、送、配能源系统中得到了极高重视[1-2]。然而，以时为单位呈现出较为明显的间歇性、随机性的光伏、风力发电由于缺乏有效的动态调度系统，电压越上、下限的情况时常发生[3-4]。为了提高片区供电的稳定性，保障各新能源电站的公平性，主网调度将对所有新能源电厂进行定值限负荷，以此会导致区域动态供电经济性较差。因此，如何解决风、水、光以及垃圾等新能源利用率低的难题，成为了当今电力研究的热点。

目前，多种新能源互补电力系统常采用与大电网系统相连，并根据不同时刻的供需关系选择与主网互供或者独立运行，于是基于预测的动态调度控制成为了研究热点[5-7]。预测主要包括负荷预测和发电量预测，常用的方法包括以差分整合移动平均自回归模型(autoregressive integrated moving average model, ARIMA)[8]为代表的统计分析和以长短期记忆网络（long short-term memory, LSTM）[9]、循环神经网络（recurrent neural network, RNN）[10]为代表的人工智能。其中，以时间序列的自相关分析为基础的ARIMA不需要大量数据进行训练，相对于LSTM、RNN具有架构简单、准确率高的优势，故常用于短期预测。但是，由于新能源中的光伏发电在日夜交替时存在近乎垂直的梯度变化、风力发电随机波动性极强，使得数据时序性极差，进而导致了ARIMA预测准确率大幅降低。另一方面，提高多种新能源经济调度控制的方法包括集中式优化和分布式优化[11-12]。以粒子群、混合整数规划为代表的集中式优化方法，对集控通信网络要求严苛，然而现实中的各个新能源电厂通信设备参差不齐，并且主网调控只能通过电话告知的方式对各电厂发电量进行调度，导致实时性、实用性较差。而以交替方向乘子法(alternating direction method of multipliers, ADMM)[11]、同步型交替方向乘子法(synchronous alternating direction method of multipliers, SADMM)[12]为代表的分布式优化方法通过分解原函数、扩增函数实现调度与控制的并行优化，在分散式多种新能源系统中应用较为广泛。其中的SADMM将上一次迭代结果所对应边界变量的平均值作为下一次迭代的固定值，实现了异步计算的ADMM转换到同步计算。但是，SADMM所采用的上一次边界变量平均值存在梯度性，不能准确反映光伏在夜间无法发电的情况，造成了调控准确率较低的问题。

针对光伏、风力发电的规律以及SADMM的不足，文中提出一种基于预测控制的多种新能源互补电力系统动态调度模型，该模型在多种新能源互补的电力系统中具有较高的经济性。

1 多种新能源互补电力系统分析

多年的调度数据表明，用户用电最高负荷、最低负荷和日总负荷的环比变化较低，一般在±4%以内，故本文视短期内每日的总负荷、各时段用户负荷相同。

1.1 多种新能源互补电力系统网络拓扑分析

西南某市的多种新能源电力系统互补拓扑图见图1。该系统以220 kV为核心，不仅包含风力发电厂、光伏发电厂、垃圾发电厂，还包含了水电厂和主网，是典型的多种新能源互补电力系统。设该片区风力发电功率为光伏发电功率为水力发电功率为垃圾电厂发电功率为大电网提供的功率为220 kV片区内用户的用电功率为该片区理想情况下电力充足，多种新能源均发电的供需关系可视为微网自主运行，此时的发电-用电数学模型可表示为：

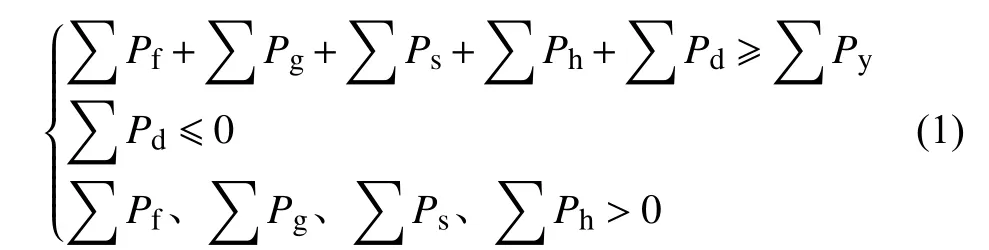
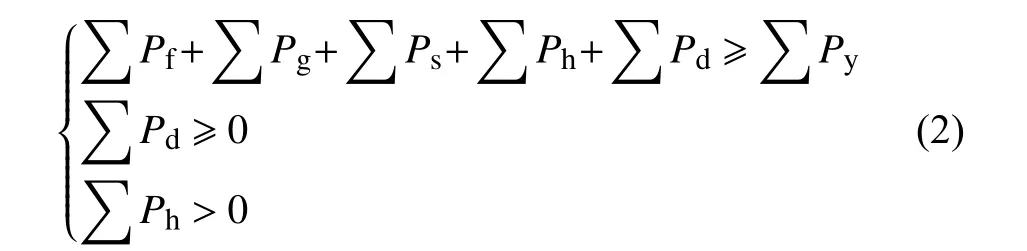
对比公式(1)和(2)可知，如果继续采用原SADMM的迭代方法进行调控，会由于循序渐进迭代值与光伏发电垂直梯度不匹配，导致该片区供电不足。即实际情况下，夜间已为0，而SADMM由于迭代值存在梯度，此时的不为0，甚至远大于0，这将导致从主网得到的较小，造成实际供电量远小于实际用电量的后果，电压越下限导致用户无法用电的风险增加。

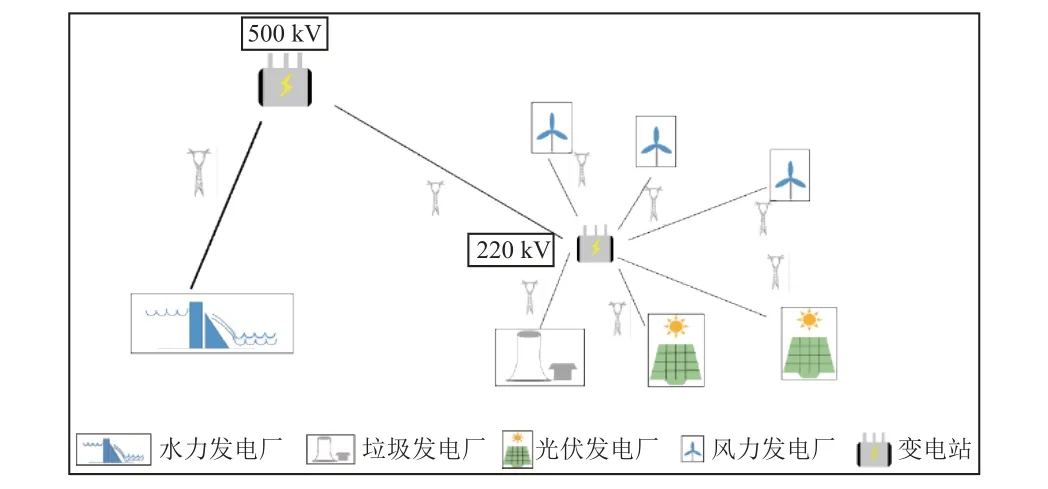
图1 西南某市的多种新能源电力系统互补拓扑Fig.1 The complementary topology of a power system containing multi-renewable energy sources in a certain city in South-west China

1.2 多种新能源发电数据分析

图2 和图3分别为每天各时刻光伏发电功率和风力发电功率，共计1周。从图2光伏隶属度函数[13]可知，以小时为单位的光伏发电具有较强的时间规律，即发电和停电有较明显的界限。从图3(a)可知，以h为单位的风力发电随机性极强，为此本文采取无穷分割的微积分思想，对风力发电时间序列进行分割，即发电采集间隔为0.25 h，如图3(b)所示由于采用了更小的采样间隙，风电随机波动梯度得到了减低，时序性得到了提升。

图2 光伏一周内各时段发电功率Fig.2 Power generated by PV in various time periods within a week

图3 风电一周内各时段发电功率Fig.3 Wind power generated in various time periods within a week k

2 基于预测控制的多种新能源互补电力系统动态调度模型

图4为随机选取一段时间内实际用电情况与动态调节、定值调节的关系效果图，从图中可知实际负荷在S1—S6时段是波动的，以定值对发电厂进行出力限制将出现大量越限告警，即：如果以40%进行限电，S1—S2时段将出现轻微越上限、S3—S4时段将出现严重越下限告警；如果以30%进行限电，则S1—S2时段、S4—S6时段将出现严重越上限告警。从图4中还可知，理想情况下的动态负荷调节由于预知后续可能出现的负荷，可提前对后续发电厂的出力进行调节，实际用电量与发电量差距较小，不仅使得电网经济运行，还能保障电压长时间处于正常范围。

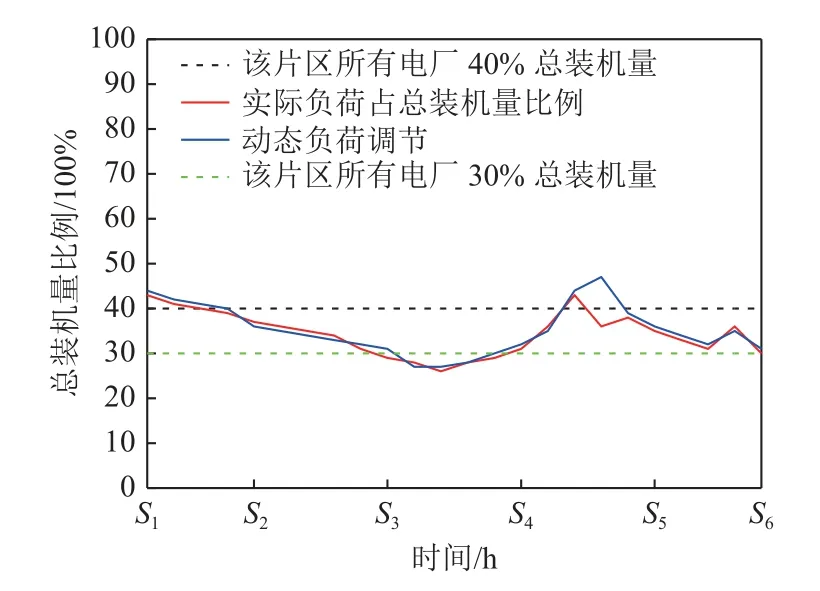
图4 实际用电情况与动态调节、定值调节的关系效果Fig.4 Relationship among actual power consumption,dynamic regulation and fixed value regulation

因此，根据预测到的用户负荷和新能源发电功率进行动态调控成为了关键，基于动态负荷预测和动态控制建立的系统如图5所示，本文将对ARIMA、SADMM两个模型进行改进。

2.1 改进自适应阈值隶属度的小波滤波光伏发电数据分析模型

从图2中可知光伏发电不仅时间性显著，还会有如同周三、周日一样的随机波动，造成数据平稳性、时序性较差。为此，本文利用隶属度作为修正参数对自适应阈值的小波滤波进行改进，通过改进后的滤波模型消除光伏发电时间性和随机波动的问题。传统的小波滤波常用阈值选取λt公式为[14]：

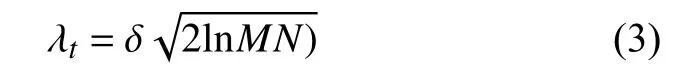
式中：δ 为噪声均方差；N为信号提升层数；M为信号范围。

针对图2中光伏发电数据的随机噪声，以及极强的时间性，本文利用隶属度函数[13]对自适应阈值的小波滤波进行改进，改进后的阈值λt′为：

2.2 改进ARIMA发电负荷预测模型

相比于LSTM、RNN等算法，ARIMA对短期内的发电量进行预测虽然有不需要大量数据训练的优势，但是白天光伏发电、夜间光伏不发电，以及风电时序规律性较差导致了数据梯度较大、平稳性差，若直接利用ARIMA 进行预测将导致预测发电量误差较大。用于短期发电量预测的常规ARIMA(p,d,q)[15]模型可表示为：

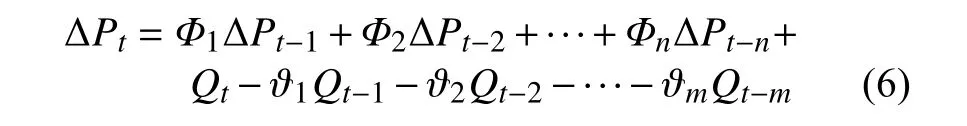
式中： Φi( i=1,2,···,n)为自回归系数； ϑj(j=1,2,···,m)为滑动系数； ∆Pt为 d阶平稳时间序列； Qt为误差项。

从图2和图3的对比可见，风电不仅预测难度要高于光伏，而且发电量也高于光伏，夜间对电网的影响较大，故本文着重对风电进行预测研究。从图3（b）中可见，在一个趋势上随机波动的风电可分解为：趋势的“倾向性”[16]和随机波动的“伊藤过程”[17]。

于是，本文在ARIMA基础上针对风电的“倾向性”，对t时刻的进行ARIMA(p,d,q)×(P,D,Q)r乘积[16]，即：

图5 基于动态预测和动态调度的调度模型Fig.5 Dispatching model based on dynamic prediction and dynamic scheduling

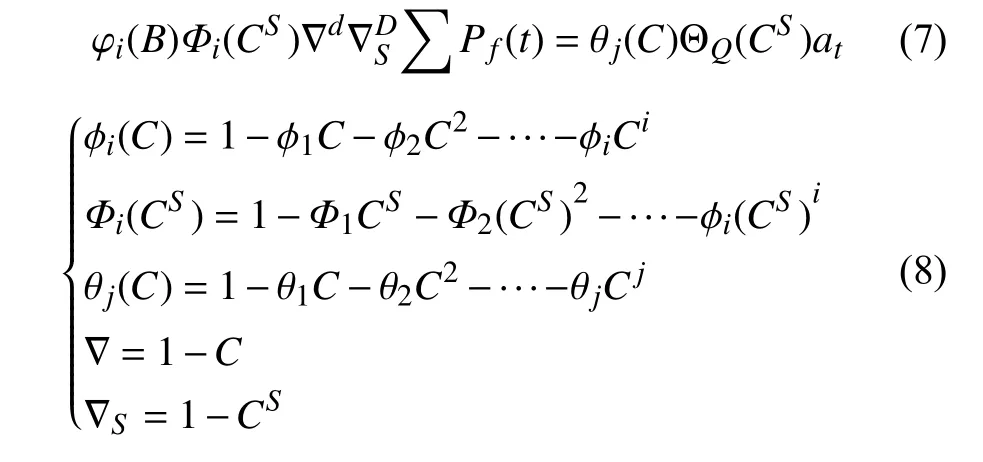
式中：C、at分别为后移数子、白噪声；d和D为差分阶数。

为了消除随机波动，进行了伊藤过程[17]乘积ARIMA模型改进：

式中：Wt为维纳标准特性随机过程；为风力发电量ΣPf向期望移动趋势；为t时刻Wt的随机性对的随机影响。

2.3 改进SADMM动态调度配电模型

从1.2节可知，由于光伏、风力发电时序性和梯度性相对于水电、垃圾发电厂较差，而且用户用电变化较小，定值的限制负荷虽然勉强保障电压正常范围波动，但是依旧不能从根本上解决电压越限问题，该方法弃风情况严重，经济性较差。此外，如果直接用SADMM[12]进行调度控制将导致实际供电量小于实际用电量的情况。两个互联区域x1、x2的标准SADMM选取上一次迭代结果作为下一次计算的固定值，其内部条件F1(x1)、F2(x2) 主要考虑了损耗成本，可表述为：

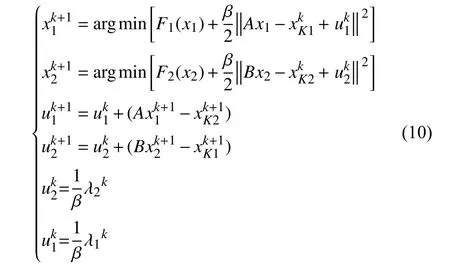
式中：A、B分别为系数矩阵；k、β、λ1、λ2分别为迭代次数、大于0的常数、第1部分的增广拉格朗日乘子向量和第2部分的增广拉格朗日乘子向量；分别为第k次迭代的边界值；F1(x1)、F2(x2)为不同区域的成本；分别为两个互联区域x1、x2内部变量更新。

从式(10)可知上一次迭代值作为下一次迭代计算固定值的方法虽然快速更新了该区域负荷，但由于没有考虑到电压约束问题将导致电压越限。本文在标准SADMM的基础上进行了改进，具体包括将后续发电负荷预测值代替上一次迭代值，并根据后续用户负荷进行动态调度。以夜间的风电和用户之间的供电关系为例，式(10)改为：

3 实验验证

考虑到白天用户用电量巨大，垃圾发电厂、水力发电厂的出力均匀、平稳，风力、光伏发电即使不平稳，其多余的发电量也可以被用户消纳或者进入大电网中，白天电压越限情况较少。本文以西部某220 kV变电站为例进行试验，该片区垃圾发电功率视为固定值，其功率为10 MW，由于水电经主网对本片区供电，本文视其功率为无限大。此外，西部片区以水电、光伏、风力发电为主，不用考虑火力发电（垃圾发电厂除外），故本文不用考虑环境污染因素。

3.1 基于改进ARIMA算法的发电和用电负荷预测

通过LSTM、ARIMA和改进ARIMA预测算法对后续负荷、发电量进行预测，以均方根误差(root mean squard error, RMSE)[18]作为评价标准：

图6 光伏原数据经小波滤波和自适应小波滤波后的结果Fig.6 Result of original PV data after wavelet filtering and adaptive wavelet filtering

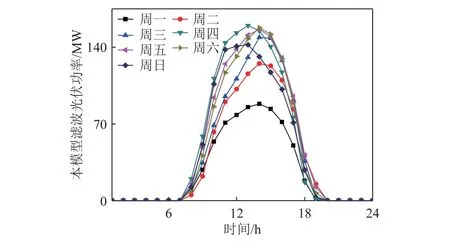
图7 本文改进方法对光伏发电数据进行滤波后结果Fig.7 Result of PV generation data filtrated by the improved method proposed in this paper

光伏原数据经小波滤波和自适应小波滤波后的结果见图6，本文改进方法对光伏发电数据进行滤波后结果见图7。从图6和图7的对比可知，经过本文方法滤波后的光伏发电数据真实性得到了还原，周三和周日由于环境因素产生的随机波动噪音得到了有效抑制，8:00—19:00光伏发电的时间性得到了保留。

图8 本文改进ARIMA、LSTM、ARIMA的预测值与用户实际负荷的对比Fig.8 Comparison of consumer’s actual load with the load forecasted by original LSTM and ARIMA respectively and that forecasted by the ARIMA improved in this paper

图9 本文改进ARIMA、LSTM、ARIMA对风力发电的预测值与发电厂实际发电功率的对比Fig.9 Comparison between the predicted Generating power by improved ARIMA, LSTM, ARIMA and actual generating power of the power plant

本文改进ARIMA、LSTM、ARIMA的预测值与用户实际负荷的对比、对风力发电的预测值与发电厂实际发电功率的对比、及对光伏发电的预测值与发电厂实际发电功率的对比见图8、图9和图10，LSTM、ARIMA、本文改进ARIMA的预测值与实际值的对比见表1。由于光伏时间性较强，夜间不发电的部分由0取代，故图10部分时间段发电功率为0。从图8—10可知，本文改进ARIMA的负荷预测SRMSE相比LSTM、ARIMA分别降低了57.4%、65%，风力发电预测的SRMSE相比LSTM、ARIMA分别降低了67.1%、68%，光伏发电预测的SRMSE相比LSTM、ARIMA分别降低了68.9%、86.9%。这说明，本文改进ARIMA模型利用“乘积”和“伊藤”的方式消除了风电随机性和光伏时间性，符合光伏、风电发电的规律。此外，结合表1、图8、9、10可知，LSTM、RAIMA预测随机性强的风力发电和时间性强的光伏发电的准确率高于负荷预测准确率，是由于本文采取了“无穷分割”的微积分思想将采样周期由1 h改为0.25 h，越小采样周期得到的数据时序性、平稳性越强。后续将另文赘述小采样周期提高预测准确率的方法。

图10 本文改进ARIMA、LSTM、ARIMA对光伏发电的预测值与发电厂实际发电功率的对比Fig.10 Comparison of actual power generated by power plant with PV generated power forecasted by original LSTM and ARIMA respectively and that forecasted by the ARIMA improved in this pape

表1 LSTM、ARIMA、本文改进ARIMA的预测值与实际值的SRMSE对比Table 1 Comparison of the root mean square error (abbr.RMSD) of actual value with the RMSD from original LSTM and ARIMA respectively and that from the ARIMA improved in this paper

3.2 基于预测控制的电力系统动态调度模型

主网不下电的情况下该片区实际发电-用电缺额、预测发电-用电缺额见图11。从图11中可知，如果没有大电网向该片区注入电能，0:00—12:00、16:00—24:00将出现大规模缺电，即使运维人员可以及时从大电网进行调度其余电能，此期间将产生大量电压越下限告警；而12:00—16:00，将出现部分电压越上限告警。

图11 主网不下电的情况下该片区实际发电-用电缺额、预测发电-用电缺额Fig.11 The actual power generation-vacancy of power consumption and forecasted power generation-vacancy of power consumption of this district when the main grid does not provide power

但是，经过改进的SADMM根据预测用户负荷、发电功率对该片区进行动态调度的方法，可将发电-用电的差额缩减至4 MW以内，如图12所示基于预测控制的改进SADMM动态控制下该片区发电-用电缺额可见，在此期间即使有大的波动，也能给调度员有足够的时间进行操作，极大降低了电压越上、下限的告警，可能出现电压越上、下限告警的时间，理论上可由原来的20 h降为1.9 h，告警降低率可达到91%，解决了新能源消纳问题。此外，相比于传统调控方式，本文方法可以在保障本片区供电充足、电压稳定的情况下，将白天多发的90.35 MW通过主网运送到其余片区，相对于该片区所有新能源1783.5 MW的发电量而言，电网运行经济性提高了5%。

此处需说明，风电、光伏、垃圾发电采用动态的统一发电比例，是由于现实中需要保证各电厂装机比例的公平性。

图12 基于预测控制的改进SADMM动态控制下该片区发电-用电缺额Fig.12 The power generation-vacancy of power consumption of this district under dynamic control of improved SADMM based on predicted control