轻质高熵合金Al20Li20Mg10Sc20Ti30弹性性质第一性原理的研究
2021-06-10唐壁玉
王 玮,丁 凝,杨 锦,杨 敏,孟 虹,唐壁玉
(广西大学化学化工学院,广西 南宁 530004)
自从2004年Yeh团队[1]及Cantor团队[2]各自独立制备出多主元合金以来,多主元合金在材料领域受到大量的关注。传统合金材料是以一种或两种金属元素为主体,再向其中加入其他金属元素或非金属元素,以达到增强性能或降低成本的目的。这样的成分设计使得传统的合金材料存在于成分相图的顶角附近部分。不同于传统合金材料的成分设计,多主元合金的主体元素有5种或5种以上,这些元素中的每一种元素的摩尔比都在5%~35%之间,这使得合金配比在成分相图中的分布,由相图的边缘区域转移到了相图的中心区域,从而大大扩展了材料成分的设计空间,因此是对传统合金成分设计概念的一个突破。
传统的合金设计认为,当合金中包含多个主体元素时,基于一些金属元素之间具有较强的键合作用等原因[3],合金中会形成大量成分不同的化合物,尤其是可能会形成大量的脆性金属间化合物,导致合金的性能不能满足应用要求。然而,多主元合金包含多个主体元素,且呈现出简单的单相无序固溶结构(包括面心立方结构、体心立方结构、密排六方结构)。出现这种有别于传统认知的现象,是由于当多主元合金形成单相无序固溶结构时,会具有比有序金属间化合物或中间相更大的构型熵。由热力学定律G=H-TS(G代表吉布斯自由能,H代表焓,T代表温度,S代表熵)可知,当温度大于0K时,吉布斯自由能随着焓的增加而增加,随着温度及熵的增加而减小。这使得单相无序结构有可能在一定温度下会比相应的有序结构更加稳定,从而出现上述有别于传统认识的现象,因而多主元合金又常被称作高熵合金。
高熵合金具有四大核心效应,即热力学上的“高熵效应”、动力学上的“迟滞扩散效应”、结构上的“晶格畸变效应”和性能上的“鸡尾酒效应”。这四大效应使得高熵合金具有一系列有别于传统合金的优异性质,例如高强度、高硬度、耐腐蚀及耐热性能等[4-7]。因此,高熵合金在结构材料、耐热材料、耐腐蚀材料等方面都有广阔的发展前景。作为交通运输行业尤其是航空航天领域重要研究方向之一的轻质合金材料,在合金的密度、强度、延展性、加工性能、耐热性能等方面提出了越来越高的要求。由于有别于传统的合金成分设计,轻质高熵合金材料作为一种新型轻质材料,受到了广泛的关注,也成为轻质合金材料研究的热点之一。
迄今为止,已经报道的密度较低的高熵合金有Senkov等人[8]制备的Cr-Nb-Ti-V-Zr体系,Stepanov等人[9]制备的AlxNbTiVZr (x=0,0.5,1,1.5)难熔高熵合金,Tseng等人[10]制备的Al20Be20Fe10Si15Ti35合金,李锐等人[11]采用感应熔炼之后浇铸的方法制备的Mgx(MnAlZnCu)100-x(x为原子百分比,x=20,33,43,45.6、50)系列合金,以及Youssef等人[12]制备的一种成分为Al20Li20Mg10Sc20Ti30的低密度高熵合金等。在上述轻质高熵合金中,密度最低的为Mgx(MnAlZnCu)100-x系列合金(密度在2.20~4.29g·cm-3之 间),以 及Al20Li20Mg10Sc20Ti30高 熵 合 金(密 度为2.67g·cm-3),它 们 的 密 度 都 达 到3g·cm-3以下。虽然这2种高熵合金都具有低密度和高硬度,但Mgx(MnAlZnCu)100-x系列合金中,除了Mg含量最高的Mg50(MnAlZnCu)50之外,其他材料都是脆的,且Mg50(MnAlZnCu)50的塑性变形程度为1.8%,而本文所研究的Al20Li20Mg10Sc20Ti30高熵合金中包含了价格昂贵的Sc元素。可见,轻质高熵合金在性能改进以及原料选择等方面还有待进一步的研究。
Al20Li20Mg10Sc20Ti30低密度高熵合金在原料球磨处理后形成的初始结构为面心立方结构,且在500℃退火1h后,晶体结构转变为少见的密排六方结构。由于其具有明显高于其他纳米晶合金的比强度,因此在航空航天等领域具有巨大的应用潜力。然而,关于此合金的FCC结构及HCP结构的弹性性质目前还没有具体的研究。本文采用第一性原理计算方法结合特殊的准随机结构,对FCC结构的Al20Li20Mg10Sc20Ti30高熵合金的弹性性质进行研究,并根据计算结果,对材料的力学稳定性、延展性和弹性各向异性等性质进行预测,以期为此材料的进一步研究及应用提供参考。
1 计算方法
采用特殊准随机结构[13]来处理高熵合金中的化学无序排列,通过合金理论自动化工具包(Alloy Theoretic Automated Toolkit, ATAT)中的“mcsqs”命令来执行[14]。针对单相的FCC结构与HCP结构,分别按照1×2×5及2×2×5扩胞生成了包含原子的超胞,之后采用基于密度泛函理论的VASP(Vienna Ab-initio Simulation Package)软件包来进行从头计算[15-16]。其中,采用投影缀加波(projector augmented-wave, PAW)[17]来描述电子和离子之间的相互作用,并采用Perdew、Burke和Ernzerhof提出的广义梯度近似(GGA-PBE)[18]来处理体系的交换关联能。2个结构计算时的平面波截断能都为500eV。FCC结构和HCP结构的K点网格设置分别为8×4×2和6×6×2。
在结构优化过程中,对于FCC结构,在平衡体积附近等间隔地取7个体积,进行形状和体积都固定的弛豫计算,得到能量-体积数据点,并采用以下的三阶Birch-Murnaghan状态方程(BM3-EOS)[19],对这些能量-体积数据点进行拟合。

其中的E0、V0、B0分别代表平衡体积、平衡能量和零压下的体模量,B′0代表V0时体模量对压力的导数,x=(V/V0)。拟合可以得到平衡体积,从而得到稳定结构的晶格常数。对于HCP结构,通过全弛豫计算,得到稳定结构的晶格常数。在结构优化过程中,超胞的电子自洽的总能收敛标准为10-4eV,离子弛豫的总能收敛标准为10-3eV。结构优化之后,采用能量-应变方法计算2种结构的弹性性质,具体计算方法可以参考文献[20-21]。弹性计算过程中,超胞的电子自洽的总能收敛标准为10-6eV,离子弛豫的受力收敛标准为10-3eV·(Å)-1。
2 结果与讨论
2.1 基态晶格常数
本文采用第一性原理计算方法,对FCC结构及HCP结构的Al20Li20Mg10Sc20Ti30高熵合金的弹性性质进行研究。先对其进行结构优化,优化的晶格常数列于表1中。从表1可以看到,计算得到的FCC和HCP相的晶格常数与实验值符合得较好,误差分别只有2.38%和3.84%。

表1 FCC与HCP相稳定结构的晶格常数和相应的实验值
2.2 单晶弹性常数
弹性行为是指固体材料在一定形变范围内可以恢复到原来状态的行为[22],通常用单晶弹性常数及多晶弹性模量来描述材料的弹性性质。单晶弹性常数(以下简称弹性常数)是反映材料在弹性范围内对外加应力的响应的物理量。在应变足够小时,应力与应变满足Hooke定律,弹性常数即为应力和应变的比值[23]。弹性常数可以提供与材料的力学稳定性、强度、硬度及延展性等性质相关的信息。FCC结构只有3个独立的弹性常数,即C11、C12和C44,而HCP结构则有5个独立的弹性常数,即C11、C12、C13、C33和C44。计算得到的2个结构的弹性常数列于表2。

表2 FCC结构和HCP结构的弹性常数
根据Born稳定性准则[24],对于FCC结构,结构稳定需要满足条件:C11+2C12>0,C11-|C12|>0及C44>0。而对于HCP结构,结构稳定需要满足条件:C11-|C12|>0,C44>0及(C11+C12)×C33-2(C13)2>0。计算得到的FCC结构和HCP结构弹性常数都符合Born稳定性准则,因此2个结构在零温零压下都是力学稳定的。
2.3 多晶弹性模量
一般来说,相对于单晶弹性常数,多晶弹性模量(包括体模量B、剪切模量G、杨氏模量E、泊松比ν)更具有实用价值[25]。多晶弹性常数可以通过Voigt-Reuss-Hill (VRH)近似而在单晶弹性常数的基础上计算出来[26]。其中,Voigt近似和Reuss近似分别代表了多晶弹性模量的上限和下限。对于FCC结构,体模量 B可以直接由单晶弹性常数获得:
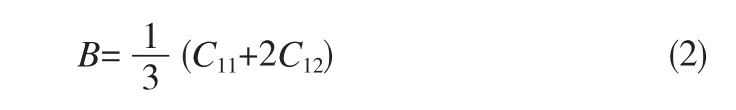
而Voigt近似和Reuss近似给出G的上下限表达式分别为:

其中的下标V和R分别代表Voigt和Reuss近似。最后可以得到G值:

对于HCP结构,Voigt近似给出的B和G上限表达式分别为:

Reuss近似给出的B和G下限表达式分别为:
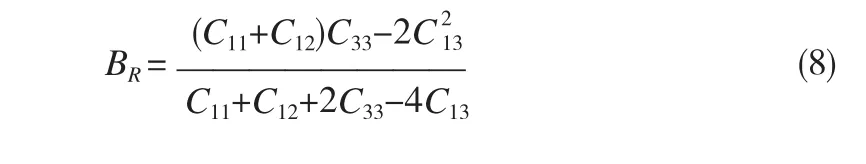

最后可以得到VRH的平均值:

其中的下标V和R分别代表Voigt和Reuss近似。得到B和G之后,两种晶体结构都可以通过以下公式来计算杨氏模量和泊松比。

计算得到的B、G、E的结果绘于图1中。从图1可以看到,HCP结构比FCC结构具有更大的体模量,表明HCP结构在外界压力下具有更好的抵抗体积变形的能力。剪切模量G是材料在外界施加剪切应力时,抵抗可逆剪切变形的能力,剪切模量越大,原子间键的方向性越强;剪切模量越小,则位错越容易滑移,从而材料的延展性越好。杨氏模量E反映材料的刚度,一般来说,杨氏模量越高,材料越硬。从图1可以看到, FCC结构具有比HCP结构更大的杨氏模量及剪切模量,表明FCC结构具有更大的硬度,这与实验报道一致。

图1 FCC结构和HCP结构的多晶弹性模量
泊松比ν可以用来衡量材料在剪切作用下的稳定性,其范围通常在-1~0.5之间[28]。泊松比越大则材料的延展性越好。计算得到的FCC结构与HCP结构的泊松比分别为0.276与0.303,表明HCP结构相对于FCC结构具有更好的延展性。Pugh’s模量(B/G)常被用来估算材料的脆性/延展性[27],当B/G>1.75时,材料具有延展性,否则材料是脆性的。计算得到的FCC结构与HCP结构的B/G分别为1.90与2.21,其值都大于1.75,表明2个结构的材料都具有延展性,且HCP结构的B/G值更大,表明其延展性更好。
2.4 弹性各向异性
材料的弹性各向异性与材料中裂纹产生的几率密切相关[29],对于工程应用具有重要的参考价值。为了比较本文中的FCC结构与HCP结构这2种不同晶体结构的高熵合金的弹性各向异性,选用Ranganathan和Ostoja-Starzewski提出的通用各向异性因子AU来表示其各向异性的大小[30]。AU通过以下公式计算:

其中GV、BV、GR、BR分别是用Vogit方法和Reuss方法计算得到的剪切模量与体模量。由于Vogit方法和Reuss方法分别代表弹性模量的上限与下限,所以GV/GR≥1,BV/BR≥1,因此AU≥0。当AU=0,材料为各向同性;当AU>0,材料为各向异性,且其偏离零值越大,表示材料的弹性各向异性越大。FCC结构与HCP结构的各向异性参数列于表3中。从表3可以看到,FCC结构比HCP结构具有更大的弹性各向异性,其差值主要来自于Vogit方法和Reuss方法计算得到的剪切模量的比值GV/GR的差异。

表3 弹性各向异性参数
3 结论
本文采用第一性原理,研究了面心立方结构与密排六方结构的轻质高熵合金Al20Li20Mg10Sc20Ti30的弹性性质。结果表明,2个结构都是力学稳定的且都是延展性材料。相比较而言,HCP结构具有更好的抗压缩能力及更好的延展性,而FCC结构具有更好的抗可逆剪切变形能力及更大的硬度。弹性各向异性的研究结果表明,2种结构的材料都为弹性各向异性材料,且HCP结构的弹性各向异性更大。
