铁路货车轴承内圈故障动力学仿真分析

丁东升， 刘永强， 李长健

(1.石家庄铁道大学 省部共建交通工程结构力学行为与系统安全国家重点实验室，河北 石家庄 050043；2.石家庄铁道大学 机械工程学院，河北 石家庄 050043)

0 引言

我国铁路货运发展迅速，在铁路货运带来巨大经济效益的同时，铁路货车的安全运行显得格外重要。轮对轴承作为铁路货车最关键的部件之一，其具有结构复杂、承受载荷大、运行环境恶劣等特点，因此在铁路货车运行中极易产生故障，如果故障不能及时被发现和解除，将影响货车的安全运行，对随行人员的人身安全和货物产生很大的损害。

基于此，国内外很多学者在轴承故障诊断和动力学分析方面做了相关研究。在轴承故障诊断方面：李翠省等[1]针对铁路货车轴承产生早期微弱故障时其故障成分容易被淹没，提出了基于EEMD和谱峭度的共振解调技术，为获取轴承故障成分提供了借鉴意义。李聪慧等[2]提出了一种基于互相关—峭度和小波软阈值的EEMD降噪方法，可以更加方便地对振动信号进行降噪。侯丽娴等[3]基于共振解调技术识别出了铁路货车轴承外圈故障，为轴承故障诊断提供了实际参考。在轴承动力学方面，Jones[4]分析了球轴承和滚子轴承在所受径向载荷作用下的弹性柔度。Ma et al[5]建立了17自由度的车体-轮对-轴承模型，对轴承内圈和外圈滚道故障进行了动力学研究。Yao et al[6]研究了球轴承的动力学特性。李长健等[7]建立了高速列车轴箱轴承内圈故障轴承动力学模型，研究了滚子转速和保持架质心轨迹。吴东等[8]建立了含外圈故障的铁路货车轴承刚柔耦合动力学模型。廖英英等[9]建立了铁道车辆轴承外圈故障轴承动力学模型，并用实验验证了所建模型的有效性。张文虎等[10]根据机械系统动力学仿真软件ADAMS和Matlab/Simulink建立了圆柱滚子轴承的动力学模型，并实现了半物理仿真。

通过上述学者们的研究可以发现,国内外学者在轴承故障诊断和动力学方面做了很多工作，但目前对于轴承故障机理的研究比较缺乏。在上述学者研究基础上，以铁路货车轴承为研究对象，通过分析内圈滚道损伤的不同程度对轴承内部元件动力学响应的影响，为轴承故障诊断和故障机理的研究提供理论参考。

1 货车轴承动力学建模

197726型轴承是我国铁路货车的主力轴承，其结构主要包括外圈、内圈、滚子、保持架、隔圈等，如图1所示。

图1 197726轴承主要结构

1.1 轴承力学分析

197726型轴承是双列圆锥滚子轴承，对轴承进行力学分析对于后续的建模和仿真具有重要的意义。滚动轴承主要接触方式为线接触，如图2所示。对滚子进行受力分析，Qoj、Qfj和Qij分别为滚子与外滚道、内圈大挡边和内滚道间的接触载荷，αo、αf和αi分别为滚子与外滚道、内圈大挡边和内滚道间的接触角，如图3所示。

图2 线接触示意图

图3 滚子受力平衡图

研究轴承受力时主要依据Hertz弹性接触理论和弹性流体动压润滑理论，在线接触的前提下，求解滚子与内外圈滚道间的接触载荷时仅仅依靠Hertz弹性接触理论是不能完全解决线接触中的弹性趋近量的问题。因此，在轴承计算中，通常引用Palmgren公式[11]来计算弹性趋近量

(1)

式中，v1、v2分别为2个接触物体的泊松比；E1、E2分别为2个接触物体的弹性模量；Q为滚子所受接触载荷；lr为滚子有效接触长度。由图3可知，根据几何关系，以外滚道接触载荷为参考，列出滚子平衡方程

(2)

由式(2)可以推导出滚子与滚道、滚子与挡边间接触载荷的比例关系

(3)

联立式(1)、式(3)，基于Hertz弹性接触理论和Palmgren公式可以求得滚子与轴承内外圈滚道间的接触刚度k

(4)

根据牛顿运动定律和欧拉方程，建立内圈所受力和力矩的微分方程

(5)

式中，Fr、Fa分别为内圈受到的径向力和轴向力;Qrij为第i列轴承第j个滚子所受的径向力;Qaij为第i列轴承第j个滚子所受的轴向力;M为轴承内圈所受的倾覆力矩。

1.2 刚体动力学模型的建立

采用三维设计软件SolidWorks建立轴承的各零部件，将建立的轴承装配体以Parasolid(.x_t)格式导入到机械系统动力学仿真软件ADAMS中，设置各刚体部件材料属性，其中内、外圈材料为G20CrNi2MoA渗碳钢，滚子和隔圈材料为GCr15高碳铬钢，保持架材料为聚酰胺-66，轴承零部件的材料属性如表1所示。

表1 轴承零部件的材料属性

为了模拟轴承真实的运行及受力情况，对轴承刚体模型添加约束、驱动、接触力、载荷等操作，其中内圈与地面间建立旋转副，对所建立的旋转副添加驱动，驱动转速为500 r/min；滚子与内圈、滚子与保持架、保持架与内外圈、隔圈与内外圈之间均设置为接触关系，接触关系中考虑了库伦摩擦力；外圈与地面之间建立弹性支撑(扭簧等)，其刚度系数和阻尼系数分别为1×1012(N·mm)/deg、1×1010(N·mm)/deg；为模拟轴承在实际运行中承受的轮对及车体质量，在外圈上方中心部位施加环绕于外圈的点力来模拟分布载荷，形成承载区，轴向载荷加载位置为内圈质心处，方向由轴承外部指向轴承内部，设置完成后的轴承刚体动力学模型如图4所示。

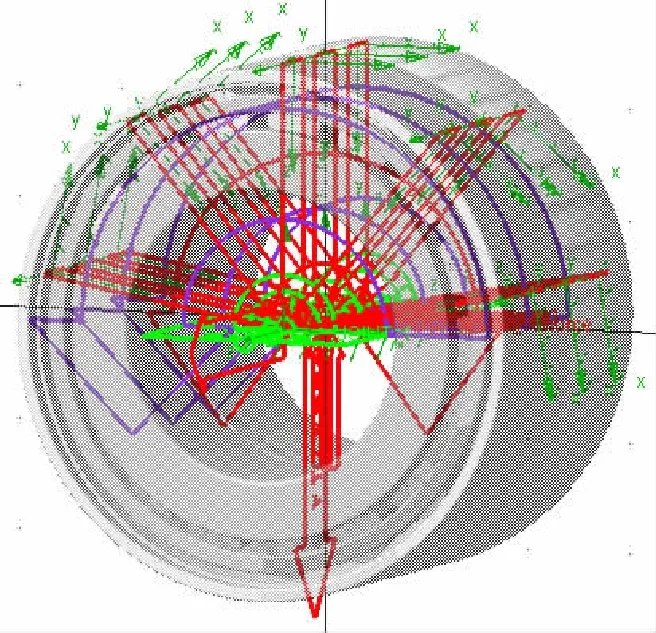
图4 轴承刚体动力学模型

1.3 刚-柔耦合动力学模型的建立

在轴承刚体动力学模型的基础上，为了更加准确地刻画轴承运行过程中轴承各部件弹性变形对其性能的影响，将轴承内圈、外圈、保持架考虑为柔性体，滚子和隔圈仍考虑为刚性体。在有限元软件ABAQUS中建立了轴承内圈、外圈、保持架模态中性文件时，最关键的两点对于能否成功生成模态中性文件很重要，一点是将建立的第一个分析步设置成线性摄动下的振动，另一点是将建立的第二个分析步设置成线性摄动下的子结构生成。模态中性文件生成后，在ADAMS中将轴承内圈、外圈、保持架刚性部件用生成的模态中性文件替换，所建立的刚-柔耦合动力学模型如图5所示。

2 故障轴承实验与动力学仿真分析

2.1 轴承故障的设置

根据调研发现，铁路货车轮对轴承最容易发生的故障集中在内圈和外圈[12]，发生故障类型最多的是疲劳剥落。本文以探究内圈滚道剥离程度对轴承动力学响应的影响为主，因此，根据实际轴承的故障尺寸大小，在实验轴承内圈滚道上采用电火花加工的方式加工一个长、宽、深为48、1、1 mm的通槽剥离故障，在三维模型轴承内圈滚道上设置一个相同尺寸的故障，如图6所示。

图6 轴承内圈滚道损伤图

2.2 实验验证

在货车轮对跑合实验台上开展故障轴承实验，将压电式传感器安装在轮对的支撑座上，用来测量实验轴承外圈处的振动加速度信号，设置信号采样频率为10 240 Hz，采样时长为20 s，设置轮对轴承转速为500 r/min。轮对轴承跑合实验台及传感器安装位置如图7所示。

图7 轮对轴承跑合实验台及传感器安装位置

将建好的刚-柔耦合动力学模型，设置仿真步长为0.001 s，仿真时长为1 s，仿真完成后，将实验信号和仿真信号经过希尔伯特包络解调得到加速度包络谱曲线，如图8所示。

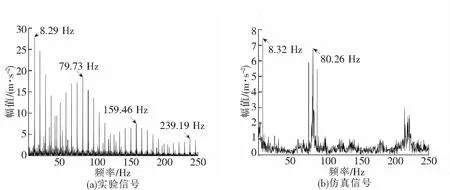
图8 实验信号和仿真信号的包络谱对比

已知轴承内圈故障特征频率计算公式

(6)

式中，r为轴承转速；n为滚子个数；d为滚子平均直径；D为轴承节圆直径；α为接触角。将相关参数带入可得，转频理论值为8.33 Hz，内圈故障特征频率理论值为80.47 Hz。

由图8可得，在实验信号中，转频为8.29 Hz，内圈故障特征频域为79.73 Hz，转频和内圈故障特征频域均与其理论值比较接近，且实验信号中可以看到故障特征频率的二倍频和三倍频；在仿真信号中，转频为8.32 Hz，内圈故障特征频域为80.26 Hz，转频和内圈故障特征频域均与其理论值十分接近；考虑到建模过程中的几何误差和软件计算中的算法误差，通过故障特征频率验证了所建轴承模型的有效性。

3 轴承动力学响应演化规律分析

在验证模型有效性的基础上，通过分析轴承内部元件间波动量、接触力、变形量来探究故障程度对轴承动力学响应的变化规律。在内圈滚道上分别设置4种不同故障尺寸，故障尺寸的长、深均为48、1 mm，故障尺寸的宽度分别为1、3、5、7 mm。为了方便对比分析，正常轴承编号正常，4种不同故障尺寸的轴承编号分别为1号、2号、3号和4号。

3.1 质心波动量的分析

正常轴承和内圈滚道不同故障尺寸下滚子和保持架质心波动量的变化规律如图9所示。

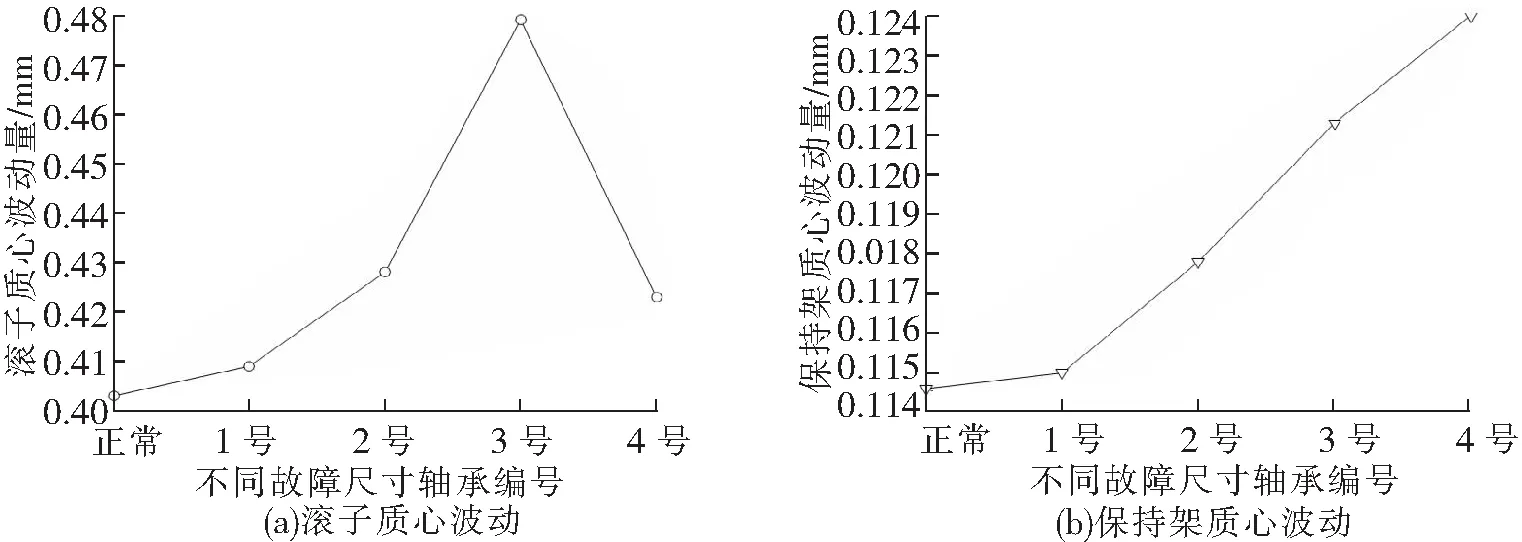
图9 波动量对比

通过图9可以得到，滚子和保持架质心波动量均比轴承无故障时滚子和保持架质心波动量大；滚子质心波动量随着故障尺寸的增加而增大，在3号故障轴承(故障尺寸宽度为5 mm)后，其质心波动量呈现下降趋势；保持架质心波动量随着故障尺寸的增加而增大，其质心波动量小于滚子的质心波动量。

3.2 滚子与滚道接触力的分析

正常轴承和内圈滚道不同故障尺寸下滚子与内圈、外圈滚道间接触力的变化规律如图10所示。

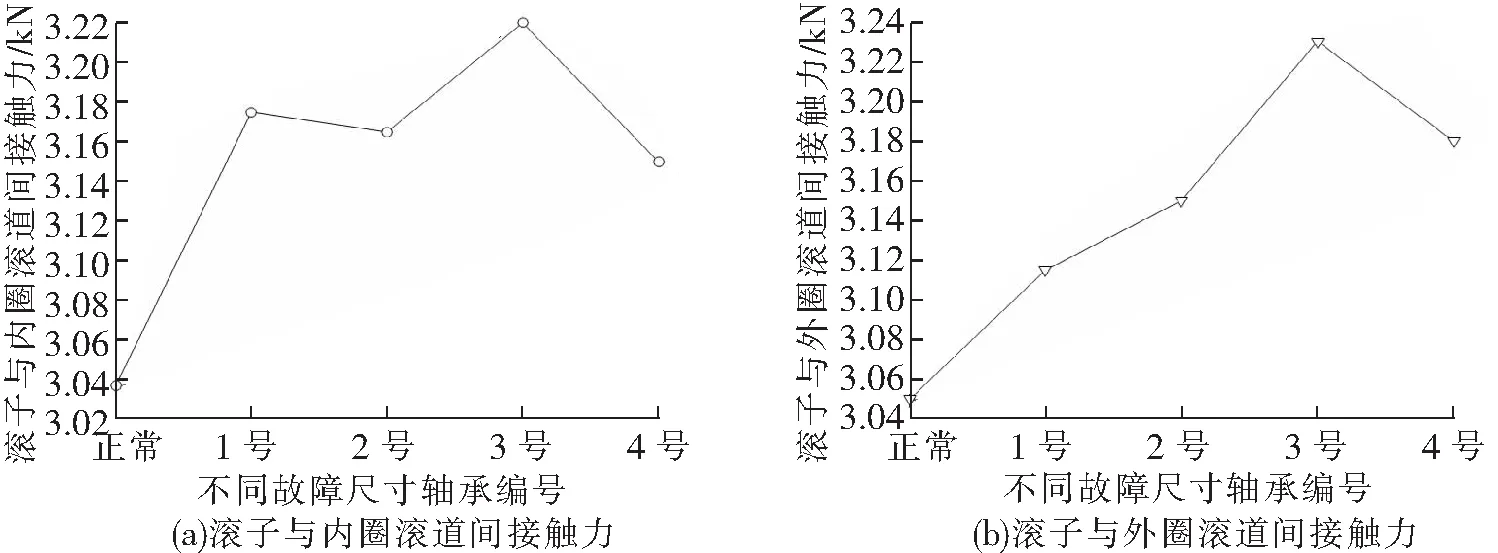
图10 接触力对比

通过图10可以看到，滚子与内圈、外圈滚道间的接触力均比轴承无故障时滚子与内圈、外圈滚道间的接触力大；滚子与内圈滚道间的接触力随着故障尺寸的增加呈现先增大后减小再增大的趋势，在3号故障轴承(故障尺寸宽度为5 mm)处，接触力达到最大；滚子与外圈滚道间的接触力随着故障尺寸的增加呈现先增大后减小的趋势，在3号故障轴承(故障尺寸宽度为5 mm)处，接触力达到最大。

3.3 变形量的分析

正常轴承和内圈滚道不同故障尺寸下轴承内圈损伤和保持架兜孔处变形量的变化规律，如图11所示。

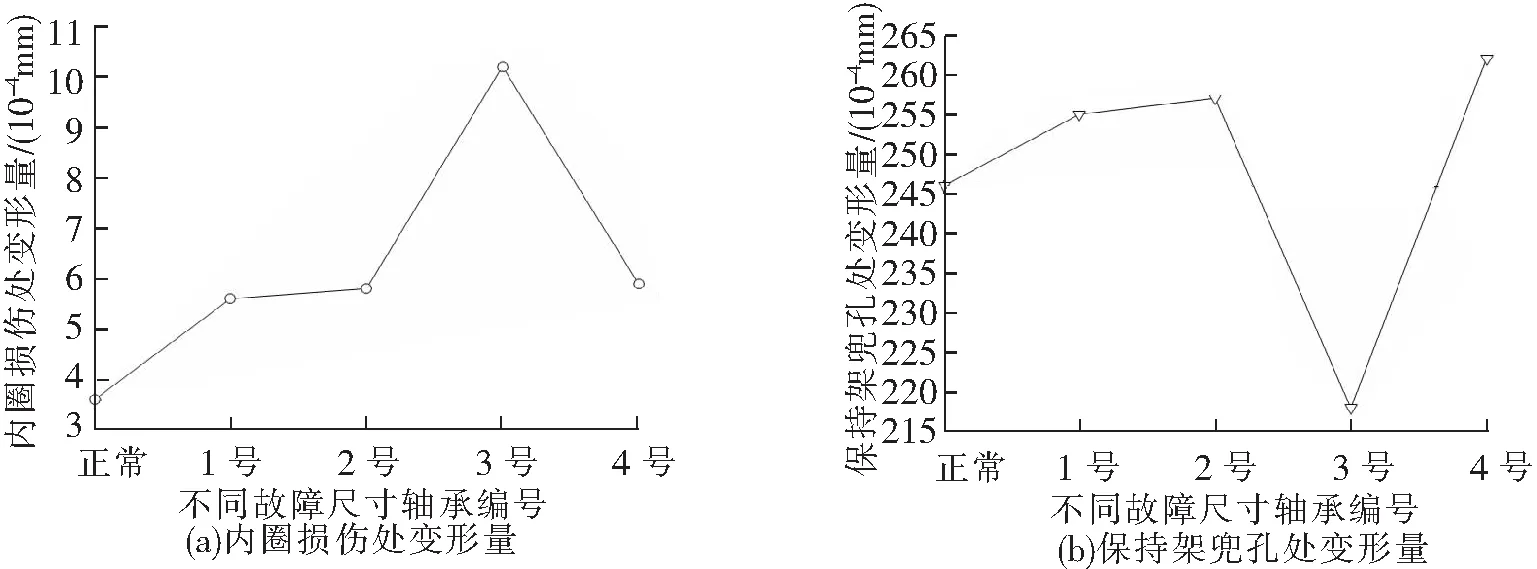
图11 变形量对比

从图11可以看到，轴承出现故障时，内圈损伤处的变形量随着故障尺寸的增加呈现先增大后减小的趋势，且内圈损伤处的变形量比轴承无故障时的变形量大，在3号故障轴承(故障尺寸宽度为5 mm)处，内圈损伤处的变形量最大；轴承出现故障时，保持架兜孔处变形量随着故障尺寸的增加呈现先增大后减小再增大的趋势，在3号故障轴承(故障尺寸宽度为5 mm)处，保持架兜孔处变形量最小，在4号故障轴承(故障尺寸宽度为7 mm)处，保持架兜孔处变形量最大。

通过对滚子和保持架质心波动量、滚子与内外圈滚道间的接触力、内圈损伤处和保持架兜孔处的变形量的分析可以发现，在3号故障轴承(故障尺寸宽度为5 mm)之前，质心波动量、接触力、变形量均随着故障尺寸的增加而增大；当故障尺寸宽度达到5 mm时，开始出现突变趋势，4号故障轴承(故障尺寸宽度为7 mm)时，滚子质心波动量、滚子与内外圈滚道间的接触力、内圈损伤处的变形量均呈现下降趋势；结合文献[13]可知，当故障尺寸增大到一定程度，随着轴承的运行，滚子一部分可以嵌入到故障区，此时，滚子与故障内壁接触，在一定程度上起到了缓冲作用，因此，在该故障尺寸对应的故障区域内，滚子质心波动量减小，其与内外圈滚道间的接触力减小，内圈损伤处的变形量因缓冲作用而降低；在滚子进入故障区时，滚子的公转速度小于保持架公转速度，此时，滚子的运动方式发生变化，由保持架推动滚子运动，因此，故障尺寸越大，保持架兜孔处变形量越大。

4 结论

(1) 综合运用SolidWorks、ABAQUS和ADAMS软件建立了铁路货车轮对轴承的刚-柔耦合动力学仿真模型，模型中考虑了轴承内部结构、约束关系、摩擦润滑和载荷驱动等。

(2) 采用轮对跑合实验和包络谱分析的方法，分析了轴承内圈存在损伤时的外圈振动加速度信号。研究结果表明，仿真信号和实验信号的故障特征频率与理论值十分吻合，该方法证明了所建模型的有效性。

(3) 探究了轴承各零部件质心波动、接触力和变形量随故障尺寸的变化规律。研究结果表明，随着内圈故障尺寸的增大，保持架晃动增强，对轴承正常运行起到阻碍作用；当故障尺寸增加到一定程度时，内圈故障处变形量、滚子质心波动、滚子与内外圈接触力均出现突变趋势，反映了内圈损伤程度大小可以通过轴承零部件动力学响应的变化趋势来判断。

本研究对铁路货车轮对轴承故障诊断和损伤程度精准识别具有理论指导意义。