系统级封装（SiP）模块的热阻应用研究

刘鸿瑾，李亚妮，刘 群，张建锋

（1.北京控制工程研究所，北京 100080；2.北京轩宇空间科技有限公司，北京 100080）

1 引言

系统级封装（System in Package，SiP）是指在一个封装体中集成一个系统。这个系统通常需要封装多个芯片并能够独立完成特定的任务，如集成了CPU、DRAM、Flash等多个IC芯片的系统级封装。现在电子产品的小型化需求已经覆盖了军用产品、航天器件、工业产品和消费类产品，SiP以其尺寸小、速度快、成本低等显著优势迅速成长为主流封装技术。随着系统集成度的不断提高，封装体内热流密度增大，SiP的热可靠性研究变得极其重要。为了保证SiP器件正常工作，每个子芯片都有最大允许结温，任一子芯片失效，都有可能导致整个系统“失灵”或“瘫痪”，因此，如何对每个子芯片进行准确的结温预测是至关重要的。

现有技术中采用的结温预测方法多采用平均热阻来进行，未考虑SiP中每个子芯片的功率分配和变化，对于功率差异较大的SiP中结温较大的子芯片容易出现严重低估的情况，这无疑会带来严重的危害[1]。

作为衡量封装模块散热能力的重要参数，热阻分析是热可靠性研究的基础[2]。为解决上述问题，本文以集成了FPGA、PROM、AD、DA的塑封SiP模块为研究对象，用热阻矩阵表示其散热性能，为芯片用户提供了一种不同温度不同功耗下封装体内部各芯片结温的快速预测方法。

2 热阻介绍

封装的散热特性一般用热阻的概念来衡量，热阻表示介质吸收1 W热量后该传热路径上介质的温升，单位为K/W或℃/W。对于单芯片封装，热阻的定义如式（1）所示：

其中，Rjx表示芯片到某一参考位置的热阻，Tj为芯片结温，Tx为参考点温度，P为芯片的功耗。对于SiP模块，Rjc表示结-壳热阻（Junction to Case），体现封装自身器件级的散热能力。Rjb表示结-板热阻（Junction to Board），体现板级散热能力。Rja表示结-环境热阻（Junction to Ambient），体现系统应用级散热能力。

在芯片应用中，各芯片都有最大允许结温，所以结温预估是非常重要的。由式（1）可得传统结温计算公式Tj=Rjx·P+Tx，公式较为简单，仅适用于预测单个芯片的结温，而SiP为多芯片组件，由于芯片之间存在相互加热现象，采用单一热阻值不能有效描述封装的散热特性[3]，若用平均热阻θjc-avg=(Tj-avg-Tc)/Q[4]，则忽略了SiP内部各芯片的功率分配和变化问题，只可得出各功率芯片的平均温度，对于结温较大的芯片，就会出现严重低估的情况，导致致命后果。

因此，本文提出在多个芯片同时发热的情况下，芯片的结温可以采用叠加原理来分析，即芯片温升等于自身加热功率造成的温升与其他芯片对其加热造成温升的叠加效果。对于一个包含n颗芯片的封装，可以采用n×n阶的热阻矩阵来描述封装的散热特性。

若SiP器件包含两颗芯片，则最终获得的热阻矩阵结构如式（2）所示：

其中Rii表示各芯片的自身热阻，Rij为耦合热阻，表示第j颗芯片对第i颗芯片的耦合加热效果。

根据线性叠加原理，包含n个芯片的SiP模块内各芯片的结温可用式（3）来计算：

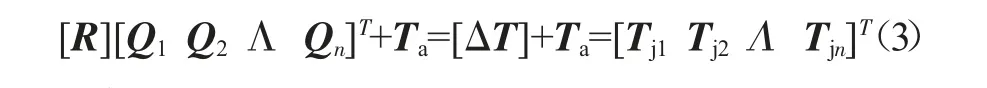
Qi(i=1～n)表示各芯片的发热功率，Ta表示环境温度，Tji(i=1～n)表示各芯片的结温。

综上，对于封装结构和热源布局确定的SiP模块，只要得到其热阻矩阵，即可得到不同温度不同功率组合下的各芯片结温。

3 热阻分析

以现有塑封SiP模块为研究对象，采用有限元仿真方法，计算结-壳热阻矩阵和结-板热阻矩阵。

图1 塑封SiP结构模型

塑封SiP模块为塑料焊球阵列封装(Plastic Ball Grid Array，PBGA)结构[5]，其基板材料为BT树脂或者玻璃层压板，密封材料为环氧树脂模塑料，焊球为62Sn/36Pb/2Ag准共晶焊料或者63Sn/37Pb共晶焊料。此处，焊球用圆柱体简化等效。SiP模块包含5颗芯片，各芯片及其最大结温和功耗估计依次为FPGA(175℃/2 W)、高速差分AD(175℃/0.414 W)、高速差分DA(175℃/0.17 W)、FPGA配置PROM(150℃/0.165 W)、8通道AD(175℃/0.0155 W)，在芯片使用中，FPGA等变功率芯片会因烧写程序不同而产生不同功耗。

3.1 结-壳热阻计算

根据研究对象实际尺寸和布局，在ANSYS Icepak模块中建立结-壳热阻（Rjc）和结-板热阻（Rjb）计算模型，见图2。划分网格时选择非结构化网格，这是因为焊球模型中包含圆柱曲面，采用非结构网格可以更好地进行贴体划分，提高计算精度。求解Rjc时，边界条件设为将封装模块放置于四周绝热的环境中，模块仅通过管壳顶部与外界环境进行换热。进行求解设置时，由于Rjc计算仅考虑传导散热，因此，在Basic Parameters操作面板中关闭对流和辐射换热，并设置环境温度为特定温度，此处为室温25℃。

图2 结-壳热阻和结-板热阻仿真模型

根据线性叠加原理，分别对各功率芯片单独施加一定的功耗，计算各芯片位置的温度。5颗芯片依次编号为0～4，得到温升矩阵[ΔT]，其中ΔTij表示第i个芯片工作时第j个芯片的温升。结-壳热阻矩阵如式（4）所示，其中Rij表示第j个芯片发热功率每增加1 W时第i个芯片的温升。

表1 单芯片工作时各芯片结温（单位：℃）

由热阻矩阵可以看出，各芯片的自身热阻，即对角线上的热阻，相比于芯片间的耦合热阻均高出3～4个数量级，这说明塑封SiP模块的表面散热能力很强，热量极易通过表面散发，耦合热阻主要体现器件的横向热传导，耦合热阻小说明横向传导作用非常小，说明热量在结-壳间传递时散热通路良好。

通过比较5个芯片的自身热阻，可以发现FPGA的热阻最小，高速差分DA的热阻最大，这是因为其余散热条件相同时，FPGA的散热面积最大，热量最容易散发，高速差分DA的散热面积最小，热量最难散发。同时，通过热阻矩阵可以比较各芯片间相互影响的强弱，以表示各芯片对8通道AD影响作用的第5行热阻为例，R54最大，表示PROM对该芯片的热作用最大。

为验证热阻矩阵的正确性，可将相同条件下通过热阻矩阵得到的理论预测温升与实际仿真温升进行对比。此处将式（4）代入式（3），并给定功率矩阵，如式（5）所示，其中高速差分AD采用了降功耗模式（0.33 W），由此可得各芯片理论预测温升如表2所示。[Q1Q2Q3Q4Q5]T=[2 0.33 0.17 0.165 0.0155]T（5）

同时在ANSYS Icepak模块中进行该工况下的实际仿真，此处设定环境温度Ta为125℃，得到实际仿真温升（见表2）。由表2可知，各功率芯片同时工作时，由热阻矩阵得到的温升和有限元实际模拟结果相比具有很好的一致性，温升预测误差小于3%。

表2 结-壳热阻理论预测与实仿对比

3.2 结-板热阻计算

计算结-板热阻时，测试环境为[6]，封装模块放置于PCB电路板上，芯片和电路板放置于密闭空间内，电路板四周的面处于恒定温度，封装模块的热量只通过电路板传导至电路板四周恒温的壁面，求得

对比式（4）和式（6）可以看出，首先，结-板的自身热阻均大于结-壳自身热阻，这是因为对于结-板，芯片热量通过焊球传导至电路板，散热面积小，散热通路较差；其次，结-板自身热阻和耦合热阻差异不足1个数量级，而结-壳矩阵中自身热阻和耦合热阻差3～4个数量级，这是因为当芯片热量不能通过表面很好地散发，就会导致横向传导作用的增强[7]，因此各芯片间互相影响，耦合热阻增大。

结合式（5）和式（6），将得到的温升与实仿温升进行对比，如表3所示。由表3可以看出，理论预测与实际仿真结果吻合度极高，验证了仿真方法的合理性。与结-壳热阻矩阵作用不同的是，结-板热阻矩阵评价了封装模块的板级散热能力，从客户应用方面来讲，已知电路板四周的恒定温度和各芯片的运行功率时，即可根据热阻矩阵很快地计算出该工况下各芯片的结温。

表3 结-板热阻理论预测与实仿对比

综上，本文开发的SiP芯片结温预估方法流程如图3所示。

图3 结温预估流程图

4 结论

本文以塑封SiP为研究对象，给出了结-壳热阻矩阵与结-板热阻矩阵的计算方法，并对封装体内各芯片的自身散热能力和芯片间热耦合作用进行了分析，仿真分析方法对同类研究有一定的参考价值。结合实际应用情况，将热阻矩阵应用于不同环境温度下以不同功率组合工作的封装内部芯片结温的预测，结果表明理论预测与实际仿真基本吻合，证明该方法有效可行。本文提出的方法是在现有产品实际应用中开发产生的，与传统单一芯片结温预估方法对比，该方法考虑了芯片间的热耦合作用，避免了各芯片功率差异较大导致的预估失真，大大提高了芯片结温预测精度，且该方法将多个计算公式集成为一个公式，降低了计算过程冗余度，提高了预测效率，这对于SiP模块的可靠性设计有重要意义。