考虑模糊区间的水库群优化调度决策方法
2021-06-09董增川陈牧风倪效宽姚弘祎贾文豪
董增川,陈牧风,倪效宽,姚弘祎,贾文豪,杨 光
(河海大学水文水资源学院,江苏 南京 210098)
近年来,随着我国各流域具有较强调节能力的控制性梯级水库的完善,流域水资源的时空调配能力得以增强,水资源开发利用方式更加多样化,流域水资源综合效益增加[1],流域内各水库在运行时不仅承担发电任务,同时在保证流域供水充足、航道畅通、维持生态多样性等方面也发挥重要作用。因此,水库群多目标优化问题的重要性日益突出,相关的研究也日益深入[2-7]。确定合理的水库调度方式也随之更加复杂,而解决这一问题的关键在于确定评价多种调度方案的指标,并合理赋权以体现指标在不同方案中的差异性和在优化结果中的重要性。由于指标的权重影响多指标决策的准确性和可靠性[8],因此确定合理指标权重是对多目标决策研究的重点。目前对于指标权重的确定方法已有了丰富的研究成果,主要有主观赋权和客观赋权两大类。常用的主观赋权法包括德尔菲法、层次分析法等,张利升等[9]构建丹江口水库考虑供水、发电等多目标的决策指标体系,并利用层次分析法得到了均衡多目的优化调度方案,为丹江口水库的调度运行提供了科学指导。但是,主观赋权法依赖于决策者深厚的工作经验,存在赋权结果偏离客观现实的缺点。常用的客观赋权法包括主成分分析法、熵值法等,周惠成等[10]将熵权的概念引入水库防洪调度多目标决策模型中,利用方案集中各评价指标的具体变异程度反映信息的效用程度,优选出最佳防洪调度方案。但客观方法只注重评价指标的客观特征,无法避免当指标特征存在较极端的取值时与现实情况不符的问题。为了克服各方法存在的问题,将主客观赋权相结合的组合赋权方法,成为发展趋势。董增川等[11]以可供水量、利津入海水量等10项指标为评价体系,利用有序二元法和熵值法的组合赋权模型优选出黄河流域水资源综合效益最大的水量调度方案;纪昌明等[12]将层次分析法和离差最大化法相结合以确定指标权重,给出了发电风险率、负荷变动风险率等新指标,评价了雅砻江流域锦官电源组梯级水电站负荷调整方案。总体上,现有的针对水库调度决策的研究已较为全面,但在分析指标权重的合理性时,决策者意向和评价指标的不确定性没有得到充分考虑,有待进一步研究。
针对上述问题,以金沙江下游为研究区,以乌东德、白鹤滩、溪洛渡、向家坝4座水库组成的梯级水库为研究对象,以梯级发电总量、适宜生态偏离度和通航保证率为目标,构建多目标优化调度模型。选取发电、生态、航运3个效益目标为评价指标,利用模糊层次分析法确定主观权重,引入区间数相离度的概念计算客观权重,并引入基于博弈论的组合赋权法,确定了均衡主客观权重的综合指标权重,从而对求解模型所得的多目标优化调度方案集进行优选分析。
1 研究区概况
金沙江为长江流域上游河段,是我国最大的水电基地,其中攀枝花以下至宜宾河段为金沙江下游,河段全长783 km,落差729 m,是金沙江流域水能资源最丰富的河段。目前,金沙江下游由上至下建设了乌东德、白鹤滩、溪洛渡、向家坝4座水库,其中乌东德、溪洛渡和向家坝水库已正式投产发电,白鹤滩水库将于2022年计划完工。梯级水库群概化图如图1所示,4座水库的特征参数见表1。
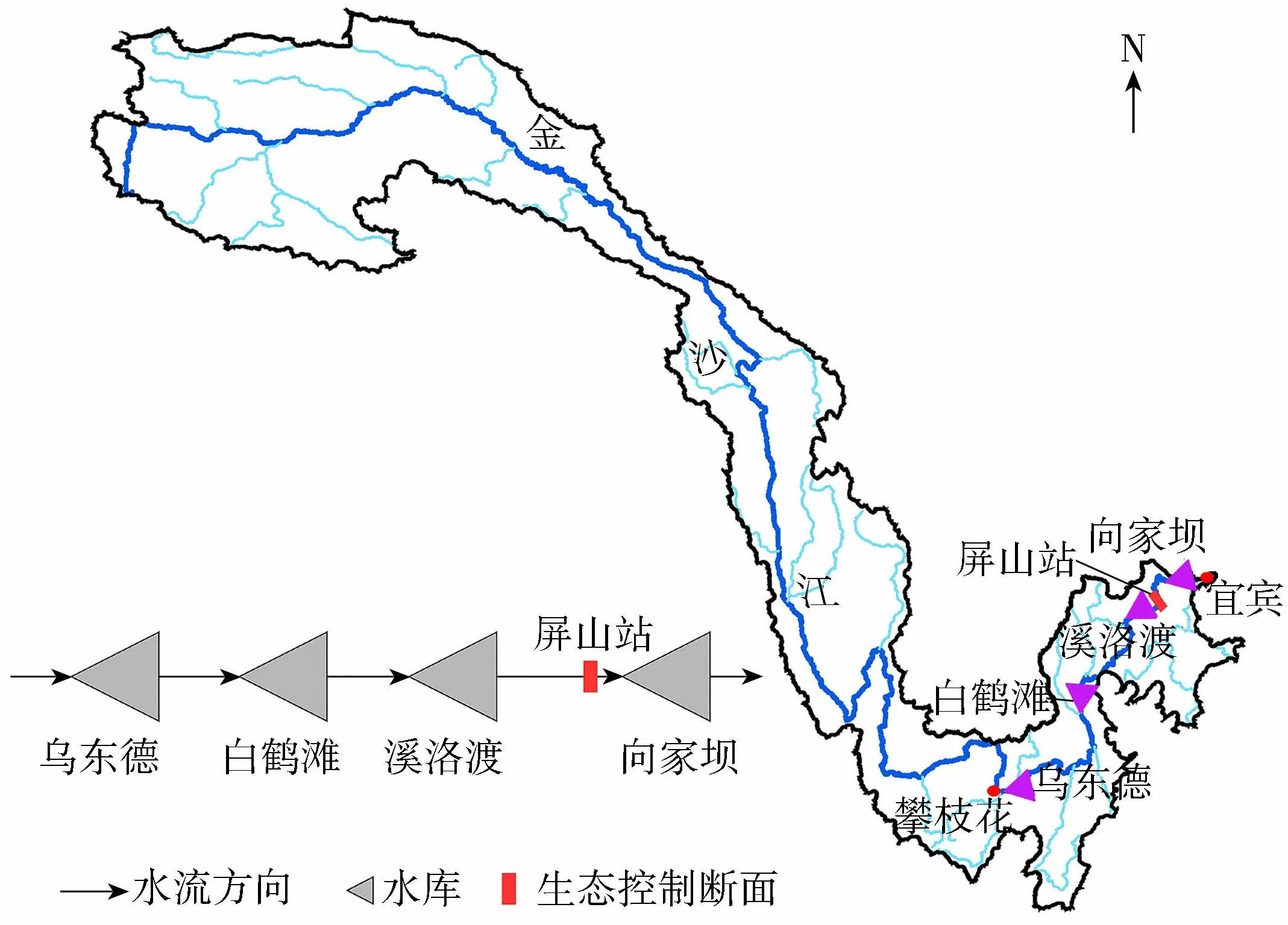
图1 金沙江下游梯级水库群概化图Fig.1 Generalization of cascade reservoirs in the lower reaches of Jinsha River
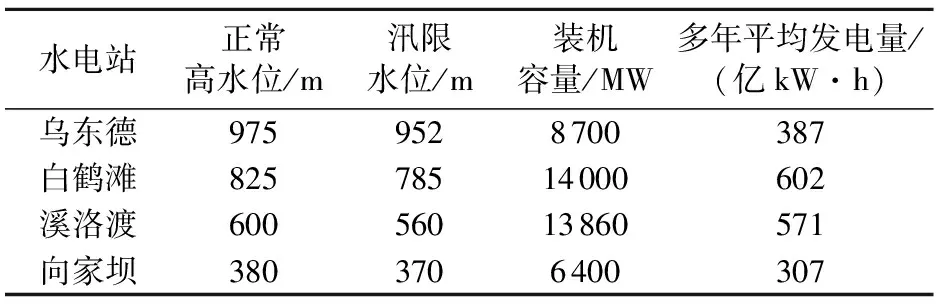
表1 金沙江下游梯级水库特征参数
金沙江下游梯级水库群为长江上游水电开发作出巨大贡献,除了发电效益外,各个水库还兼具防洪、航运、灌溉、拦沙、鱼类保护等综合作用,是金沙江流域水资源综合开发利用的重要工程性措施。
2 研 究 方 法
2.1 多目标优化模型
选择流域发电、生态、航运效益作为金沙江下游梯级水库群调度的优化目标,分别以梯级总发电量最大、生态适宜偏离度最小以及通航保证率最大为优化目标函数,构建梯级水库多目标优化模型,求解梯级水库优化调度方案集。目标函数如下:
a. 发电:梯级发电总量最大。
(1)
式中:E——梯级总发电量;Ng,t——第g库在t时段的出力;t——时段数;g——水库数;T——总时段数;Δt——某一时段长度。
b. 生态:适宜生态偏离度最小。
(2)
式中:Eco——适宜生态偏离度;qg,t、Qeg,t——第g库下游的第t月的月平均流量和生态适宜流量,其中生态适宜流量通过取50%频率的逐月频率法[13]计算得出。
c. 航运:通航保证率最大。
(3)
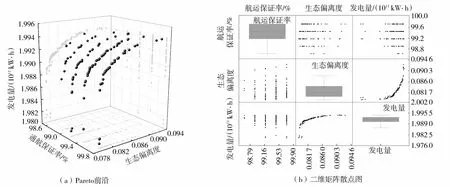
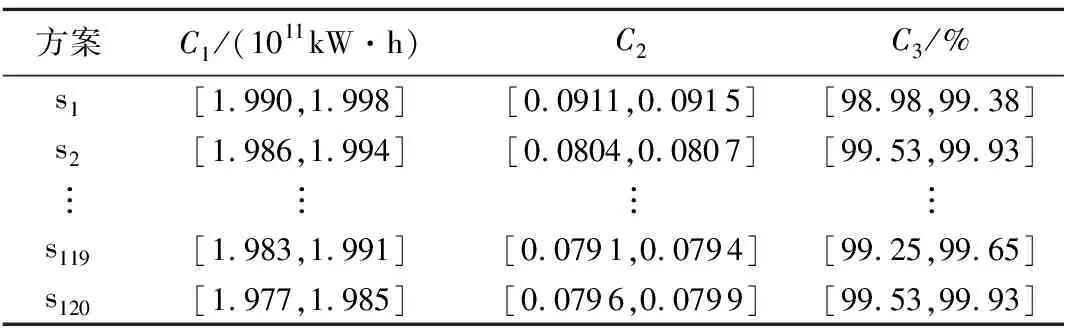
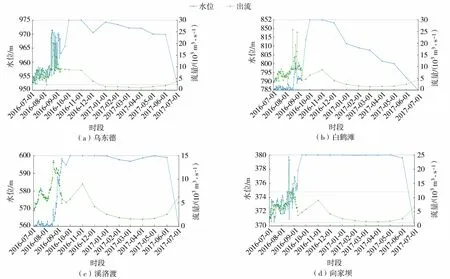
其中TH={t|QH,min 式中:H——通航保证率;QH,min、QH,max——通航河段适宜流量的上限、下限;TH——保证通航时间。 将各个水库的汛期防洪要求和流域供水控制断面的流量要求设为多目标优化模型的约束条件,此外约束条件还包括水库水量平衡约束、水库水位、出流流量约束等[14]。 2.2.1 基于三角模糊数的模糊层次分析法 专家在评判多个指标间的相对重要程度时,思维一致性难以保证,传统的层次分析法无法反映现实中人们评价事物重要性时的模糊思想,将具有不确定性的判断绝对化,并且传统方法在保证判断矩阵一致性上难度大,现有判断标准CR<0.1缺乏科学依据[15]。水库调度中评价指标间的重要性难以绝对量化,传统层次分析法忽视了其间的模糊性。三角模糊数是将模糊不确定的语言变量转化成确定数值的一种方法,用于解决具有不确定性的模糊评价问题[16]。因此,引入三角模糊数表征两两指标间重要程度的比判,构成模糊层次分析法(FAHP)。设指标集为U={u1,u2,…,un},式(4)为模糊三角函数表达形式: Fij=(lij,mij,uij)(i=1,2,…,n;j=1,2,…,n) (4) 式中:Fij——指标ui与uj间重要性比较的模糊三角函数;lij、mij、uij——指标ui相对于uj可能的重要程度的上界、中值和下界,其中两两指标间重要性定量比较1~9中的整奇数分别表示同等重要、比较重要、一般重要、强烈重要、极端重要,整偶数表示重要性介于相邻判断标准之间,若ui对uj的重要性为λ,则uj对ui的重要性为1/λ。 对各指标进行两两比较,形成判断矩阵F: (5) 各指标的初始权重为 (6) 式中:γi——指标ui的初始权重;li、mi、ui——指标ui初始权重的上界、中界和下界。 根据三角模糊函数的定义,一个指标与其他指标相比更重要的程度为 τi=v(γ≥γ1,γ2,…,γn)=minv(γ≥γi)(i=1,2,…,n) (7) 式中:τi——指标ui相对其他所有指标的重要程度;v(·)——相对重要程度的计算通式。 (8) 2.2.2 基于区间数相离度的客观赋权方法 在水库调度模型计算中,一方面由于参数选取差异、系统误差、模型概化等因素,使得计算的指标值与实际情况存在一定的误差;另一方面,由于天然的径流过程存在随机性,导致计算出的调度方案集无法精确描述水库实际运行时各评价指标的真实表现[17]。因此本研究通过区间数的形式表示各方案的指标值,从而更加贴近真实调度情况。 设多指标决策的z个待评价方案集为S={s1,s2,…,sz},而n个评价指标对应的权重向量ζ=(ζ1,ζ2,…,ζn)为待求量。将各指标值模糊化处理使各方案si关于指标uj的指标值为区间数(xij,L,xij,U),形成指标矩阵,并利用区间数运算法则,分别对效益型指标和成本型指标进行规范化处理,以消除不同物理量纲对结果造成的影响,处理后的指标值为[rij,L,rij,U],即可得规范化指标矩阵。 (9) (10) 求解此优化问题,并进行归一化处理后得到各属性的最优权重为 (11) 2.2.3 博弈论综合赋权方法 为综合主观权重和客观权重,引入一种基于博弈论的综合赋权方法。该方法将综合赋权问题变成一个多人优化问题,目的是在不同的权重之间寻找一个均衡一致的解,使得最终的可能的权重与各个基本权重之间的偏差极小。该方法的求解可转换成对式(12)中e个线性组合系数αe进行优化,使得ω与各个不同方法计算得的ωl的离差最小,本研究中ω1=Γ,ω2=ζ。 (12) 则该问题可以转化成下式所表示的优化问题: (13) 求解上式可以得到一个使多种权重赋值方法相协调均衡的综合权重结果。根据矩阵的微分性质,可得与式(12)最优化的一阶导数等价的方程组为 (14) 求解该方程组,即可得到最终的综合赋权值。 本研究以金沙江平水年2016年实测径流作为模型输入条件,其中汛期(7月1日至9月10日)以天为计算步长,旬末蓄水期(9月11—30日)以旬为计算步长,其余时期以月为计算步长,以水库各时段水位为决策变量,总计为332个。采用NSGA-III优化算法求解该模型,设置种群数为120,即有120个备选方案,得到该多目标优化调度问题的Pareto前沿,如图2(a)所示。将Pareto前沿两两投影在二维平面上,即可辨识多目标间的相互作用关系,如图2(b)所示的矩阵散点图。 图2 多目标优化调度Pareto前沿及二维矩阵散点图Fig.2 Pareto Frontier and two-dimensional matrix scatter diagram of multi-objective optimal scheduling 根据图2可以发现发电与生态间有明显的竞争关系,当水库选择发电量大的方案时,生态遭到破坏的程度增加。这主要是因为在枯水期,梯级水库运行时需要减小下泄,抬高水头以增加水库发电的水头效益,而在来水较多的时期则在保持一定水头的基础上,选择加大下泄以更好的利用水库发电的流量效益,这2种调度方式都会对水流的天然径流过程造成明显的改变,经水库调度后的下泄量与生态适宜流量存在较大的差别。而另外2组目标发电-航运和生态-航运间虽没有明显的竞争关系,但在选择方案时,仍不能保证同时达到最优,多个目标之间存在相互影响作用。 为实现水资源多目标综合利用,通过比较不同调度方式在多目标效益中获益的大小是否满足决策者要求和指标客观特征来评判其优劣,本研究选择发电量、生态偏离度和通航保证率作为方案决策评价指标,各指标的表达式同优化模型目标函数的表达,各指标值为模型优化计算结果相应值。 首先利用模糊层次分析法进行主观赋权,请多位专家对4个评级指标的重要程度进行打分,每次打分给出可能相对重要程度的上下界和中值,最终形成判断矩阵如式(15)所示,其中C1~C3分别表示发电量、生态偏离度和通航保证率3个指标: C1C2C3 (15) 对以上判断矩阵进行规范化处理后,再利用式(6)、式(7)得到各指标大于其他指标的重要程度,进行归一化后,可以计算得基于模糊层次分析法的主观权重为 Γ=(0.568,0.092,0.340) 由于在当前经济快速发展的趋势下,决策者更希望通过水库的调控作用加大流域发电效益和航运效益,以提高流域的经济实力,因此主观赋权的结果中发电效益指标和航运效益指标占比较大。 其次,利用基于区间数相离度的客观赋权法,首先对各指标值模糊化处理,本研究中取±0.2%作为指标值模糊化的上下界展开范围,模糊化后各方案的指标值见表2。 将表2转化为决策矩阵,其中梯级发电效益和通航保证率为效益型指标,生态适宜偏离度为成本型指标,将决策矩阵转化为规范化决策矩阵,再根据区间数相离度的概念,利用式(11)求得客观权重为 表2 模糊化处理后各方案指标值 ζ=(0.033,0.892,0.075) 根据客观权重可见生态效益占比最大。这主要是因为3个指标值中,发电和航运指标在各方案间的差距相对较小,而生态指标在各方案之间的差距远大于发电和航运指标,对方案的区分与选择起更明显的作用,因此生态目标的权重最大。 最后利用基于博弈论的综合赋权方法,得到均衡主观和客观因素的综合权重为 ω=(0.279,0.524,0.197) 根据综合权重,借助加权的TOPSIS法[18]在120个方案中选出相应的最优方案,优选的方案的指标值如下:发电量为1.980 9×1011kW·h,生态适宜偏离度为0.079,通航保证率为99.178%。 该方案下4座水库的水位过程和水库出流过程如图3所示。 图3 优选调度方案下各库的水位过程和流量过程Fig.3 Water level process and discharge process of each reservoir under optimal operation scheme 综合的权重均衡了主、客观的特点,既保留了生态指标在区分方案时的重要作用,也考虑了决策者对经济效益的重视程度,据此所优选出的方案也综合了主客观权重的不同侧重点。由于生态偏离度的客观权重结果远大于其余2个属性,为了证明该权重计算结果的可行性,对属性C2进行敏感性分析。根据计算结果,不考虑生态偏离度属性权重低于另外两个属性的情况,取[0.3,1)为区间,0.000 1为步长,改变客观权重中生态偏离度的权重值,重新计算规范化的客观权重以及综合权重,并借助与研究中同样的加权TOPSIS法在120个方案中优选最佳方案,发现最优方案的选择结果仍与文中选择结果相同,说明生态偏离度属性具有鲁棒性,其权重的变化对最优方案的选择没有影响,也说明了该属性对于区分方案的优劣有突出作用。由此可以证明本文中客观权重体现了属性值的客观特征,而由该权重确定的最优方案也是合理的。 优选方案的发电量仅低于所有方案中的发电量最大方案0.6%,但与通航保证率最高的方案相比仅相差2 d,且该方案的适宜生态偏离度为所有方案中最小,既保障了流域水资源经济效益的发挥,同时也保护了流域生态系统的稳定。由图3的水位、流量过程线,可以看出各个水库在汛期前期基本保持较低水位以完成防洪的任务,同时通过较大的下泄流量增加发电效益,汛期后期水位逐渐抬高直至正常高水位。汛期过后,由于来水减少,水库保持较高的水位,利用水头差加大发电,同时控制水库下泄流量满足航运和生态对流量的需求,实现流域水资源的综合优化利用。 构建了基于区间数相离度理论和模糊层次分析法的多目标调度方案优选方法,并将其应用于金沙江下游梯级水库群。该方法考虑了径流随机性和模型概化及计算时的误差造成的评价指标值浮动对评价结果的影响,解决了传统层次分析法对主观判断模糊性的绝对化问题。而基于博弈论的综合赋权法,在主观权重和客观权重之间找到一个均衡解,综合反映了决策者偏好和指标值客观离散特征,增强了决策优选中权重确定的合理性。 根据本文所述方法得到优选调度方案中的发电量为1 980.0亿kW·h、生态偏离度为0.079、通航保证率为99.178%。所选方案既获得了较高的发电效益和通航效益,又能更好地维持流域的生态环境,具有综合协调性。同时水库运行方式符合各水库在不同阶段的任务需求,具有一定的实用性。因此,本文的计算方法可行并且能对指导梯级水库群多目标优化调度决策提供一定的指导。2.2 多目标决策优选方法
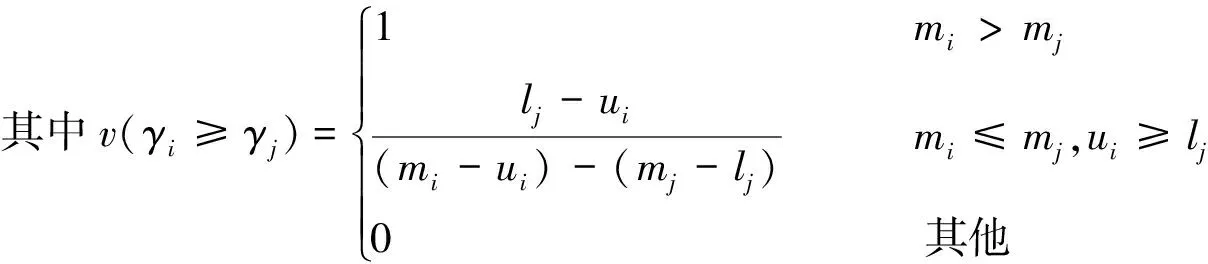
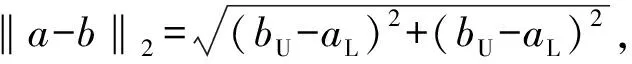
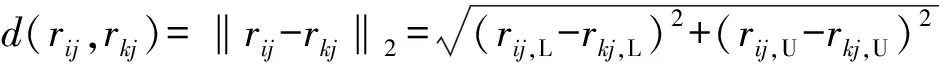
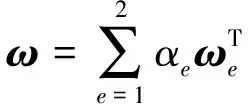
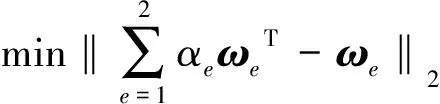
3 结果与分析
3.1 多目标优化模型计算结果
3.2 多目标决策方案优选结果
4 结 语
