高钒合金型内熔化扩散温度场及钒含量分布模拟
2021-06-08余世浩李佳琪张琳琅
余世浩,李佳琪,张琳琅
(1.武汉华夏理工学院智能制造学院,武汉 430223;2.武汉理工大学材料科学与工程学院,武汉 430070)
0 引 言
在装备制造、冶金机械、矿山开采等工业领域,许多设备零部件因使用工况非常恶劣,需兼具高强韧性和高耐磨性以提高其使用安全性和使用寿命;但是采用单一均质材料制造的零部件往往难以兼顾这两种性能。合金型内熔化扩散方法[1]是一种固液复合铸造方法,根据钒与碳反应形成高耐磨碳化钒颗粒的原理,在模具型腔底部预置高钒合金棒,浇入高温液态金属进行凝固成型,通过高温使高钒合金熔化并与金属液之间发生元素互扩散和钒碳反应,从而在铸件表层生成呈梯度分布的碳化钒硬质相,实现表层耐磨性和深层韧性的良好匹配。
目前,大多采用有限元方法对金属铸造过程进行预测进而实现有效控制。已有研究大多集中在通过有限元软件模拟常规金属铸造时的凝固温度场,结合缩孔、疏松等缺陷的热力学条件,对铸件中的缩孔、疏松以及热裂纹等缺陷进行预测[2-4]。合金型内熔化工艺由于型腔中内置的合金棒与液态金属的理化特性不同,凝固时的传质、传热过程也与常规浇铸过程不同。合金元素的扩散是影响铸件综合性能的关键因素,然而目前关于温度场对该工艺下合金元素扩散规律的影响研究尚不多见。余世浩等[5-6]研究了型内熔化扩散过程中合金元素的浓度分布,建立了合金元素扩散方程。作者采用有限元方法模拟了高钒合金型内熔化扩散温度场,根据温度模拟结果建立了钒元素含量分布的数学模型,模拟了钒元素沿铸件径向的含量分布曲线并进行了验证。
1 温度场计算模型
1.1 基本假设
合金型内熔化扩散铸造方法如图1所示。在型腔内放置高钒合金棒会导致金属液的凝固过程更加复杂,若在求解时考虑所有影响因素,则会造成计算过于复杂。因此,对凝固过程作如下假设[7]:液态金属在充满型腔的瞬间开始凝固;凝固时液态金属没有相对流动,即只考虑热传导作用;砂型温度变化较小,其热物性参数为与温度无关的常数;不考虑过冷度,即低于液相线温度后,液态金属开始凝固,冷却到固相线温度时,凝固过程结束。
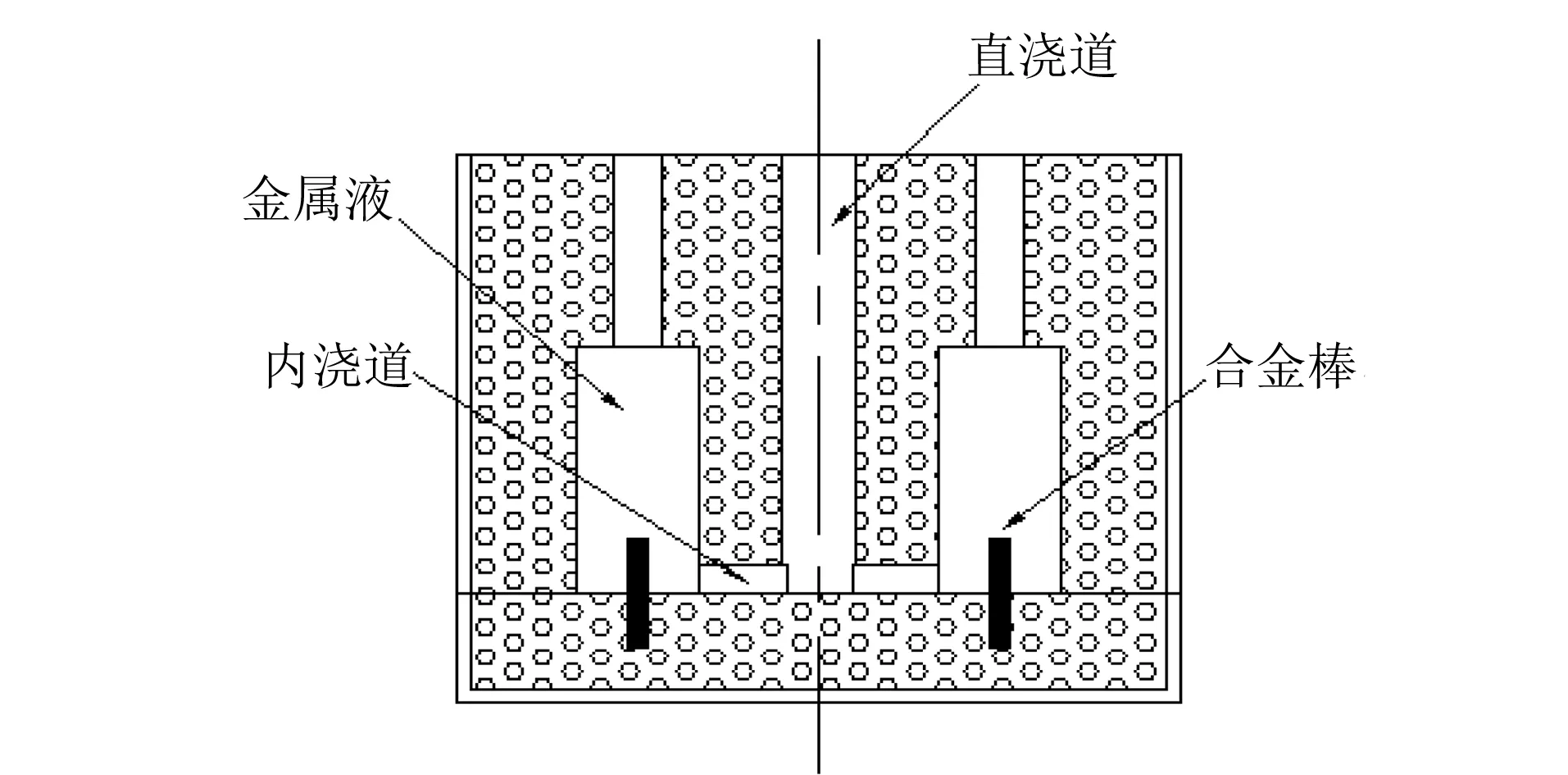
图1 合金型内熔化扩散铸造方法示意
1.2 初始及边界条件
初始条件指时间为0时型腔内的温度分布,包括高温金属液在充满型腔时的初始温度(试验温度为1 550 ℃),合金棒与砂型的初始温度(取室温25 ℃)。
基于整个铸造系统进行温度场计算,故边界条件主要指温度场的表面换热条件。金属液充满型腔后,其凝固过程实际上也是砂型向外逐渐散热的过程。在模拟时,假设铸件(扩散件)和砂型之间不存在间隙,则整个铸造系统的传热过程主要包括高温金属液、合金棒和砂型之间的传热,以及砂型与外部环境之间的对流和辐射传热。金属液浇注进型腔后,砂型表面升温不明显,热辐射较小,并且辐射传热具有显著的非线性特征。因此,为减少计算量、提高分析效率,将辐射传热造成的影响换算成对流散热,从而简化边界条件[8]。
1.3 热物性参数
在型内熔化扩散过程中,合金棒的表面温度应高于其固相线温度,从而使界面处发生冶金反应实现冶金结合。因此在金属液浇铸凝固过程中,合金棒材料会发生相变,需要考虑相变潜热对温度场的影响。
ANSYS软件可以通过定义材料参数来计算相变潜热,计算公式为
(1)
式中:H为相变潜热;ρ为密度;c(T)为比热容;T为热力学温度。
在进行相变分析时,将相变潜热作为材料特性输入模型[9]。砂型的热物性参数与温度无关[10],其导热系数为0.52 W·m-1·K-1,密度为1 630 kg·m-3,比热容为1 220 J·kg-1·K-1。V9Cr4高钒合金和5CrNiMo合金的热物性参数分别见表1和表2。
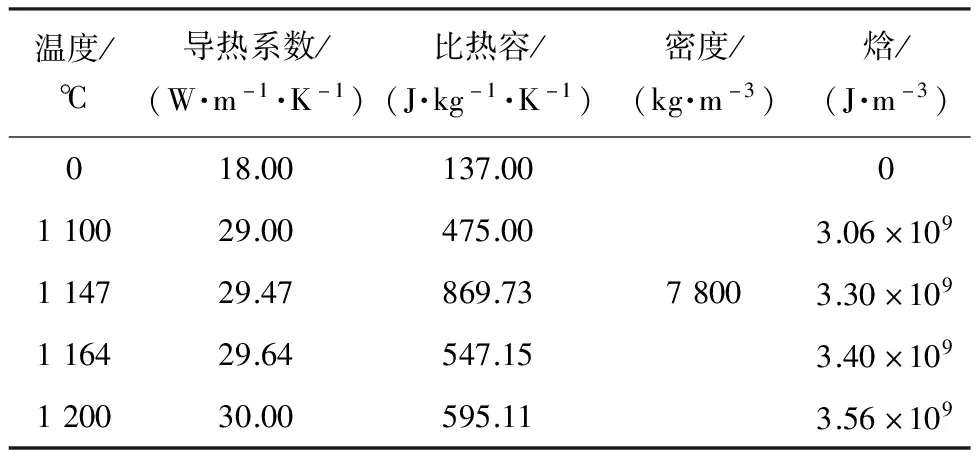
表1 V9Cr4高钒合金的热物性参数
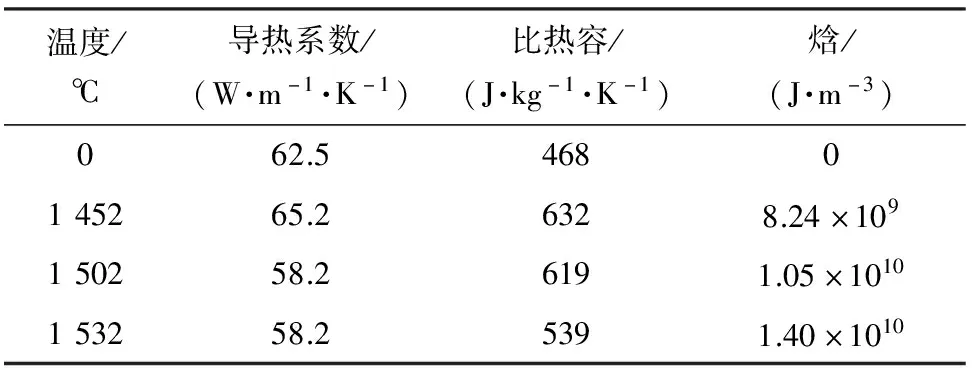
表2 5CrNiMo合金的热物性参数
2 凝固过程温度场有限元模拟及结果
2.1 有限元模型
整个铸造体系结构为对称结构,取其1/4进行研究,如图2所示。利用ANSYS软件实体建模工具构建三维实体模型,选用Solid70单元类型进行网格划分。由于合金棒和砂型的尺寸相差很大,若采用自由网格划分,会导致网格畸变,影响分析精度。因此,采用映射网格划分,结果如图3所示。
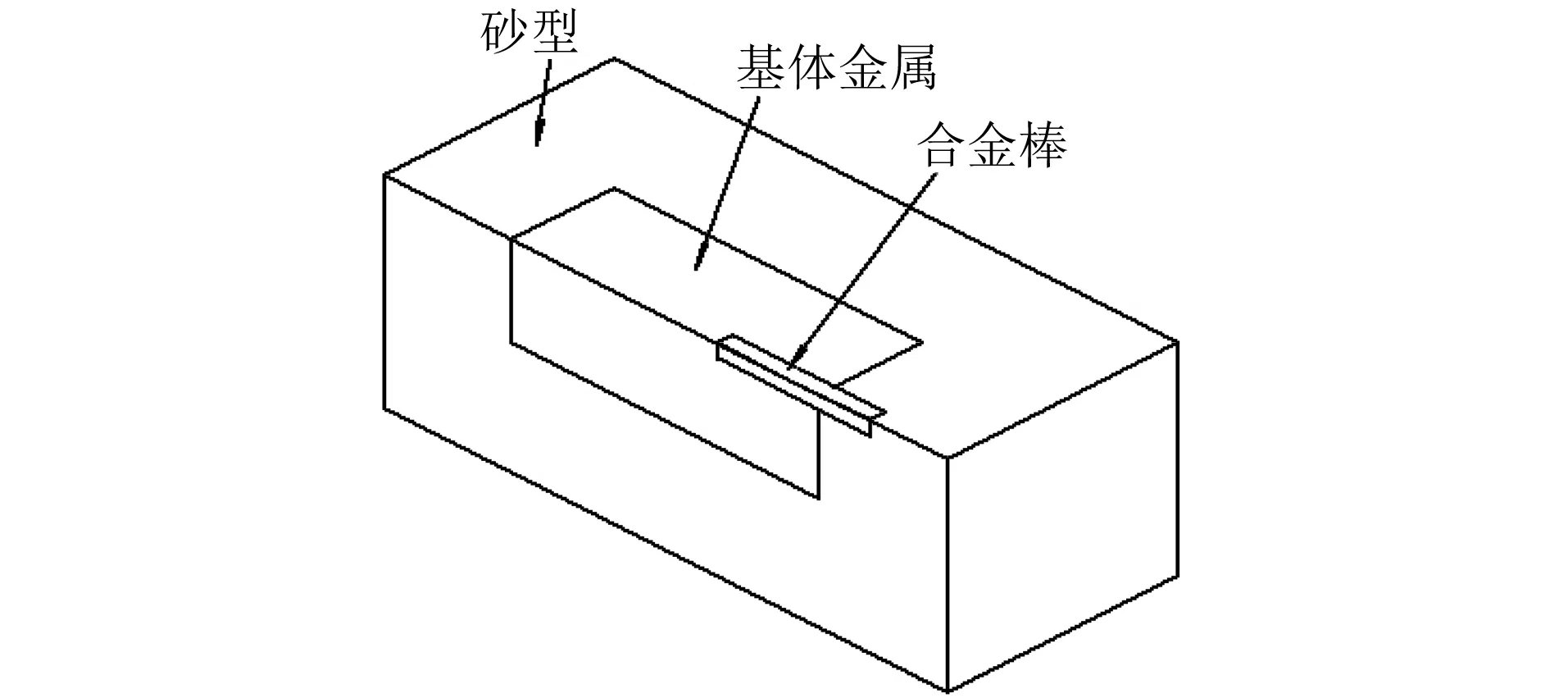
图2 1/4铸造体系结构的几何图

图3 铸件有限元模型及网格划分
2.2 加载求解
分别设定砂型、合金棒、液态金属的初始温度,并在砂型外表面施加对流载荷。设定对流换热系数为65 W·m-2·K-1,中心截面处为绝热边界。首先进行时间步长为0.01 s的稳态分析,将分析得到的温度场认定为整个瞬态分析的初始温度,然后指定分析类型为瞬态求解,载荷为阶跃施加,将自动时间步长设置为开,终止时间设置为1 000 s,研究该段时间内的温度场变化规律。
2.3 温度场模拟结果分析
为分析合金型内熔化扩散过程的温度场变化,取图4中A,B,C三点进行分析。其中,A,C为合金棒上的点,A点为合金棒端面和金属液接触的中心点,C点为与砂型端面平行的合金棒的中心点,B点为砂型端面与合金棒接触的金属液上的点。
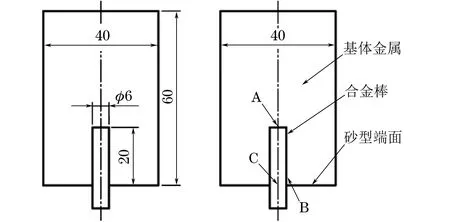
图4 扩散件结构和尺寸示意
如图5(a)所示,金属液浇入砂型后,通过热传导使合金棒温度快速上升,合金棒轴向A点和C点先后达到最高温度,而后随铸件一起冷却。A点直接接触高温金属液,其达到的峰值温度高于C点。然而由于合金棒的尺寸不大,热传导很快,冷却过程中A点和C点的温差相对较小(约30 ℃)。因此可认为合金棒周围的温度沿轴向变化不大,将合金棒径向和轴向的三维扩散简化成径向的二维扩散进行分析。由图5(b)可以发现,C点的温度低于B点,这是由于C点不与高温金属液直接接触,且合金棒的导热系数比砂型大造成的,这与实际情况相符。
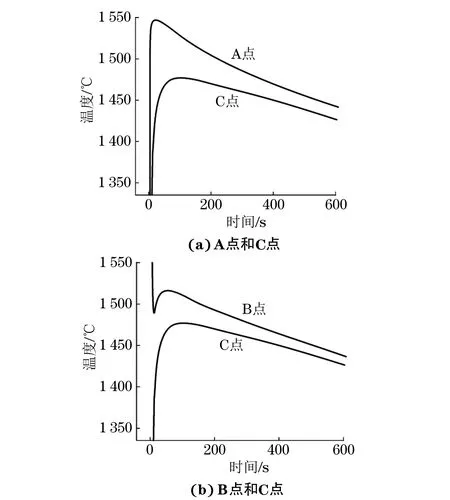
图5 模拟得到图4中不同点的温度随时间的变化曲线
液-固双金属要实现稳固的冶金结合,界面温度要达到固态金属固相线以上20~40 ℃。V9Cr4高钒合金的化学成分(质量分数)为2.5%C,0.5%Si,0.8%Mn,8.9%V,4.2%Cr,根据合金熔点计算公式[11-12]求得其熔点约为1 340 ℃。从C点的温度变化曲线可知,合金棒发生熔化,这说明该型内熔化扩散工艺可以实现5CrNiMo合金和V9Cr4高钒合金的冶金结合。
3 钒元素含量分布计算及测试
3.1 钒元素含量计算方法
高温金属液浇入型腔后,高钒合金棒表面发生熔化,钒元素向金属液中扩散迁移。整个铸造体系中各个位置点的钒元素含量随时间不断变化,为不稳定扩散,可以用Fick第二定律来描述,即:
(2)
式中:C为钒元素质量浓度;D为扩散系数;t为扩散时间;x为钒元素扩散深度。
由图5中的温度模拟结果可知,合金棒轴向温度变化不大,即可认为合金棒周围温度场分布呈圆柱状。因此,可将钒元素在径向和轴向的三维扩散简化为径向的二维平面扩散。将合金棒截面圆心设置为直角坐标系的原点,则扩散过程中钒元素沿径向的含量与时间及空间位置的关系为
(3)
式中:C0为基体金属毛细管内的钒元素质量浓度;r为合金棒端面半径;ξ为扩散区中任一点的位置。
3.2 钒元素含量分布计算结果及测试验证
对于型内熔化过程中合金元素的径向扩散行为,主要影响因素是扩散系数和时间。在高温状态下,钒元素在5CrNiMo合金毛细管内的扩散系数为3.580×10-5~3.733×10-5cm2·s-1[6]。
一般来说,合金元素在液态金属中的扩散系数比在固体金属中高2到3个数量级。因此,在型内熔化过程中,可忽略固态金属中合金元素的扩散行为,只考虑液态金属或者固液混合时合金元素的扩散,即可将液态金属/固液混合时的扩散分布看作该合金元素的最终含量分布,而扩散时间则为金属液充满砂型后到凝固结束需要的时间。5CrNiMo合金的固液转变温度为1 399 ℃,根据B点的温度模拟结果,如图6所示,可推知钒元素的扩散时间为810 s。
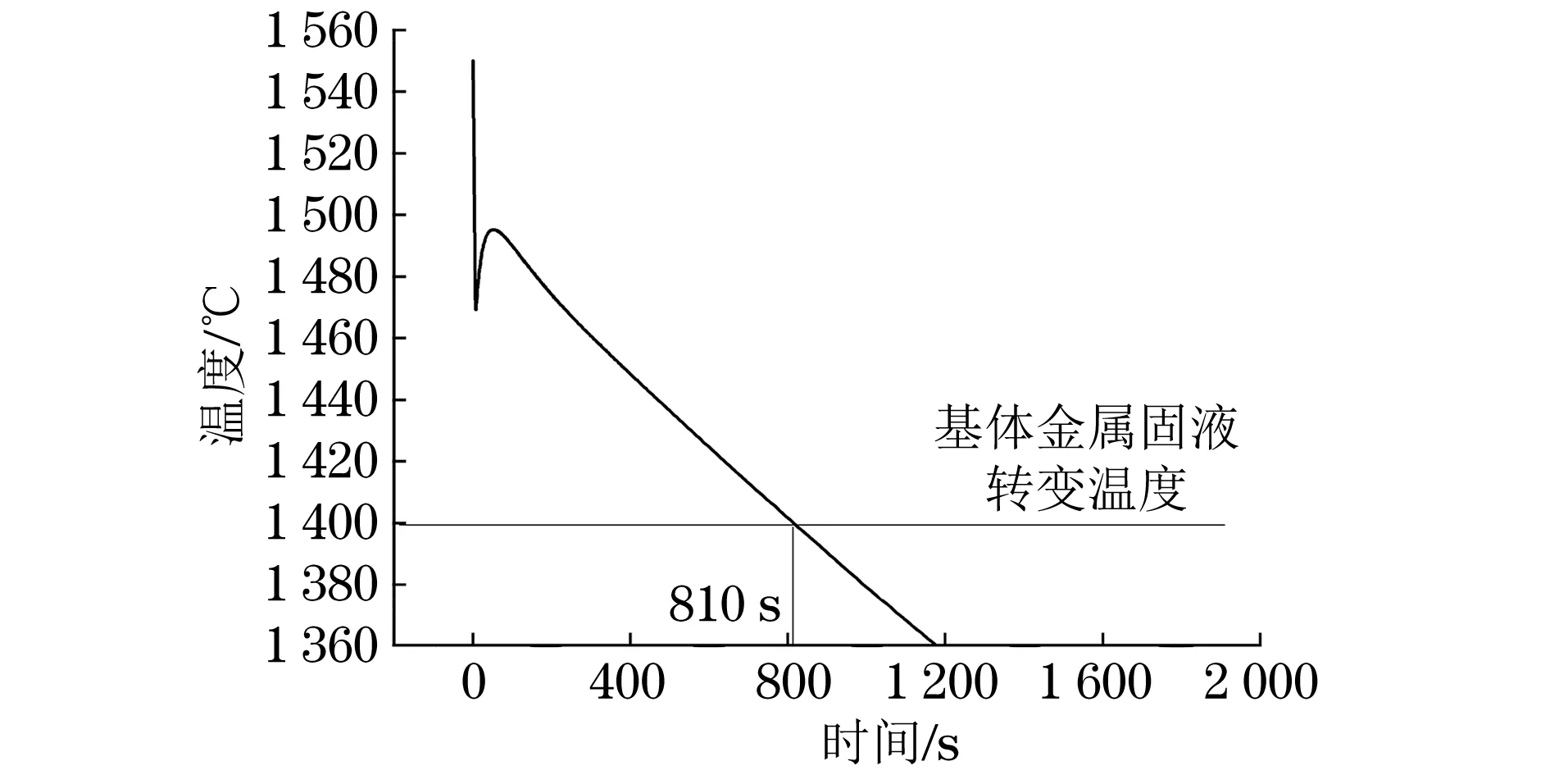
图6 B点温度模拟结果
将扩散系数和扩散时间代入式(2),利用MATLAB软件计算得到钒元素在型内熔化扩散过程中的含量分布。以合金棒横截面的圆心为原点,利用JXA-8230型电子探针沿径向对铸件进行钒元素含量检测,得到钒元素含量沿径向的分布曲线。
由图7可以看出,钒元素含量分布的计算结果与测试结果基本吻合,不同位置钒元素含量的相对误差小于1%,说明利用型内熔化温度模拟结果来计算钒元素含量分布是可行的。建立的型内熔化扩散有限元模型和钒元素含量分布数学模型,可以用于型内熔化工艺优化和钒元素扩散控制,即选择合适的型内熔化工艺参数,通过调整温度场来实现合理的钒元素含量分布。
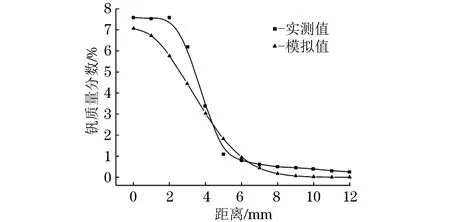
图7 铸件径向钒含量分布曲线的实测结果与计算结果
4 结 论
(1)建立了高钒合金型内熔化有限元模型,模拟结果表明合金棒温度沿轴向变化不大,可将其径向和轴向合金元素的三维扩散简化为径向的二维扩散;在浇铸金属液后,合金棒端面及内部温度均高于其固相线温度,说明合金棒熔化并与5CrNiMo合金实现冶金结合。
(2)由有限元模拟得到的温度分布曲线,可知钒元素的扩散时间为810 s;将由型内熔化温度模拟结果确定的钒元素扩散时间代入钒元素含量分布数学模型,计算得到的径向不同位置处钒元素含量与测试结果的相对误差小于1%,说明建立的型内熔化扩散有限元模型较为准确,可以利用其模拟结果来计算钒元素含量分布。
