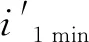基于分光计多光源三棱镜色散特性综合实验的探究性研究

张亚萍，冯振康，李汶锴，焦刘阳，李 静，周小岩

(中国石油大学 理学院，山东 青岛 266580)

早在1672年牛顿用一束近乎平行的白光通过玻璃棱镜时，在棱镜后面的屏幕上观察到一条彩色光带，这就是光的散射现象。当入射光不是单色光时，对于不同波长的光而言，在相同的入射角照射下，其出射角并不相同，表明不同波长的光对玻璃的折射率各不相同。物质的折射率与通过物质的光的波长有关，折射率n是波长λ的函数[3]。

1 三棱镜色散特性及测量原理

1.1 三棱镜的色散

介质的折射率随着波长λ的增加而减小的色散称为正常色散。对于一般透明材料而言，在可见光范围内，大部分符合正常色散。正常色散特性满足以下关系式

(1)

式(1)称为柯西(A.L.Cauchy)公式，是法国数学家柯西于1836年首次研究获得的经验公式，其中A、B、C是由所研究介质性能决定的常数[3]。本实验在分光计上，分别采用氢灯、氦灯、钠灯和汞灯几种不同光源照射三棱镜光学平面，经过三棱镜折射获取不同波长的单色光，研究三棱镜的色散特性，获取其色散特性经验公式，对基于分光计调节实验项目进行拓展和延伸，探索有别于常规实验教学的探究性实验教学内容，开设基于分光计调节基础上的设计研究性，系列综合性实验项目，并将其应用于创新性物理实验教学的探索和尝试，以期对实验教学改革起到启发促进作用。

1.2 最小偏向角法测量折射率

如图1所示，当光线射入三棱镜，在三棱镜中会发生两次折射，入射光线与出射光线间的夹角为δ，称为偏向角。将三棱镜按照图2所示放置方式，放置在载物台上，转动分光计载物台，改变入射光线与三棱镜入射面的夹角时，相应的偏向角δ也会随之改变，研究结果表明，当δ角度达到最小值时，三棱镜折射率n与最小偏向角δmin满足以下关系[3,4]

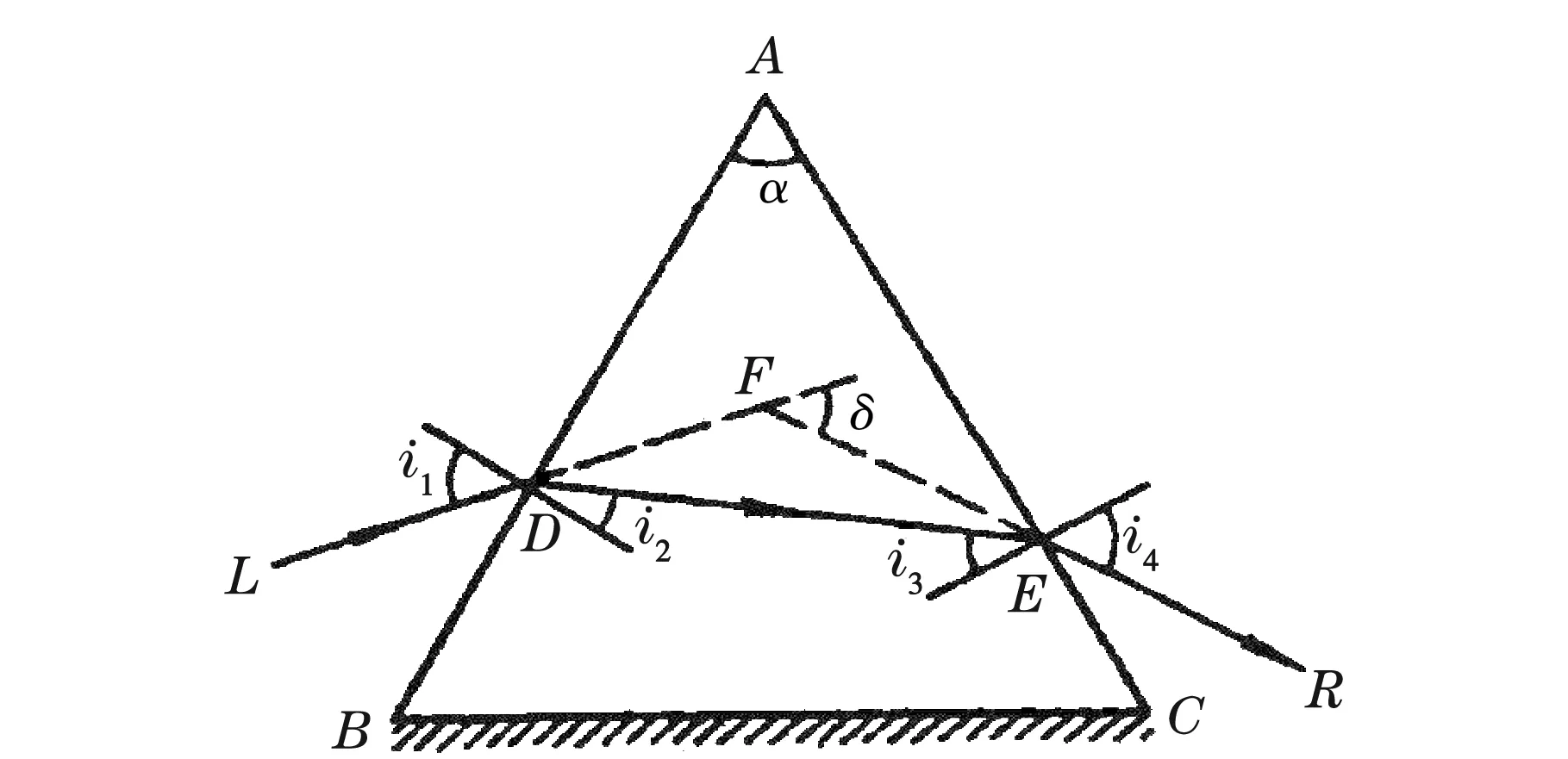
图1 光束在三棱镜中传播光路图

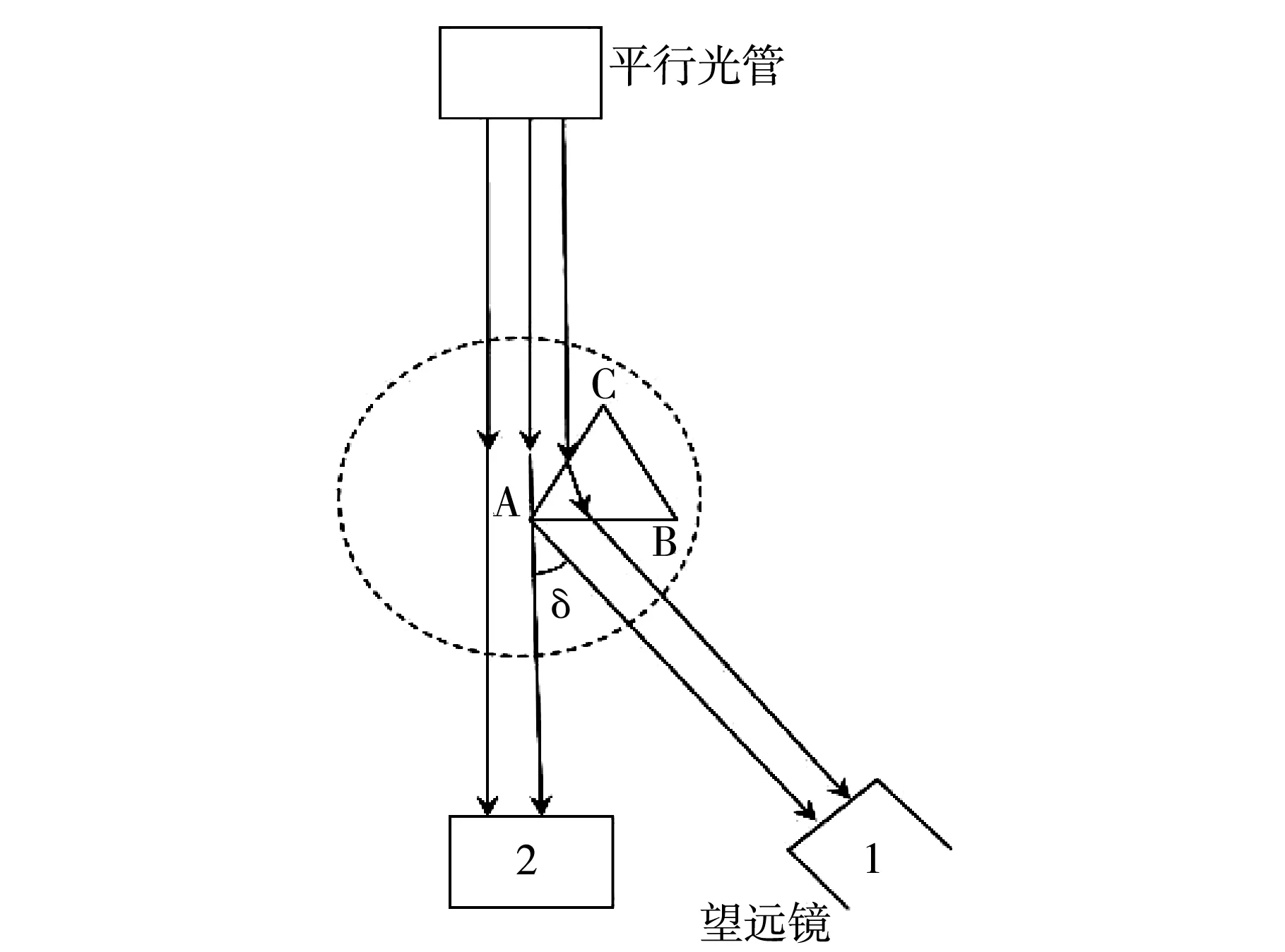
图2 最小偏向角测量示意图

(2)

式(2)中α为三棱镜的顶角，其角度大小为60°。

1.3 掠入射法测量折射率

学龄前儿童处于视觉发育的关键期和敏感期，这一时期各种不利因素均可影响屈光发育。早期发现屈光状态异常，消除不良影响因素对儿童视力保护有重要意义。为了解晋江市3～6周岁幼儿屈光状态异常发生率及其影响因素，笔者于2010年5月－2011年5月对本市3 346名3～6周岁幼儿进行屈光状态筛查及相关影响因素调查，现将结果报告如下。

图3 掠入射法原理图

(3)

式(3)中α为三棱镜的顶角，其角度大小为60°。

2 实验部分

2.1 分光计的调节

分光计的精确测量是基于对其进行调节，处于正确测量状态的基础上进行的。根据分光计的调节原理，实验测量前必须对分光计进行精确调节，分光计的调节必须满足以下要求[3]：

(1)望远镜聚焦于无穷远，使得望远镜能接收平行光；

(2)平行光管能发出平行光；

(3)望远镜光轴、平行光管光轴与分光计的中心转轴三轴垂直。

2.2 三棱镜的调节

将三棱镜放置在分光计载物台上中心位置附近，并且使三棱镜的三条边分别垂直于载物台下面的三个水平调节螺钉a、b、c连线组成三角形的三条边，如图4所示[3]。三棱镜的调节需要满足：转动载物台时，经三棱镜两个反射面反射回来的十字像与分划板上方的十字刻线相重合为止，即达到自准直。三棱镜调节完成后，就可以实现三棱镜顶角α的测量。

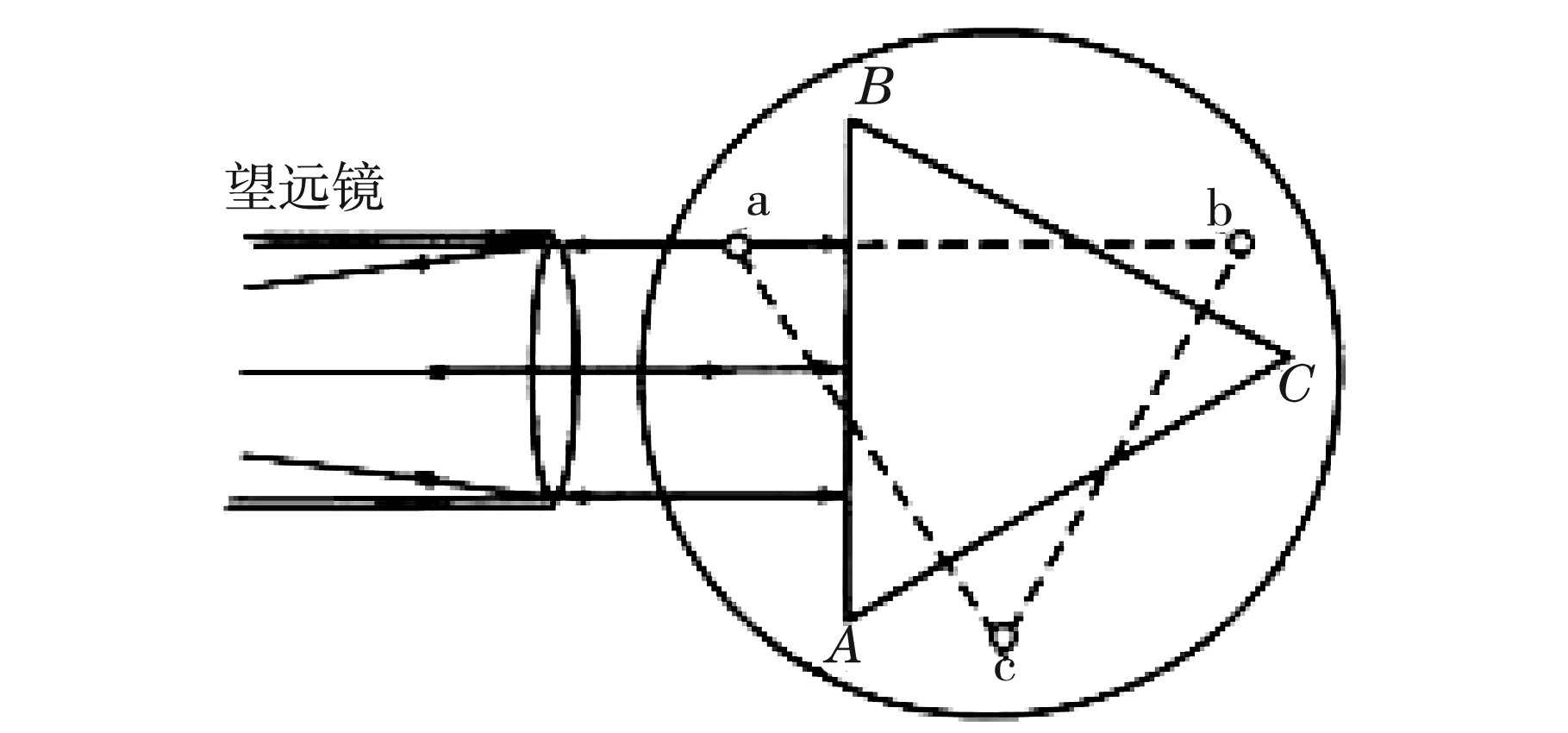
图4 三棱镜调节放置图

2.3 最小偏向角的测量

测量最小偏向角时，从分光计的望远镜目镜位置观察出射光线的彩色谱线，沿同一个方向转动放置三棱镜的载物台改变入射角的大小，彩色谱线随之发生移动，找到彩色谱线即将向相反方向移动的临界位置所对应的角度位置，再找到此时入射光线直射的角度位置，这两个位置的角度差即为最小偏向角δmin。在角度的实际测量中，为了消除分光计转动系统“偏心差”带来的系统误差，在分光计刻度盘一直径的两端相差180°位置设置2个角游标，需要记录左右2个角游标在入射角以及出射角位置的角度值θ10、θ20和θ1、θ2，则最小偏向角可用以下公式计算[1]

(4)

掠入射法的角度测量方法与最小偏向角测量方法类似。

3 结果与讨论

3.1 几种光源光谱的选取方法

所有实验测量均是在GGY型分光计上进行，并且两种方法测折射率时使用了同一块三棱镜。在测量不同光源形成的谱线时，实际的光谱与理论谱线存在着一定的差异。实验中采用的氢灯光源所形成的谱线，并非只呈现理论上的巴耳末系，巴耳末系可见光部分有四条谱线，Hα=656.3 nm(红光)，Hβ=486.1 nm(绿光)，Hγ=434.1 nm(蓝光)，Hδ=410.2 nm(紫光)[6]。用氢灯做光源最小偏向角法测量时三棱镜的色散光谱如图5所示，由图5可以看出，在红光和橙光部分，会形成较多的杂光，实验测量中，尽量选取不形成杂光区域的谱线进行角度测量，以确保谱线位置可以较准确地确定。

图5 最小偏向角法氢灯色散光谱

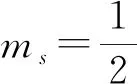
氦灯光谱的选用方法与氢原子光谱相一致，即选用能够确定位置和波长的光谱来测量。在最小偏向角法测量时，选用了5条谱线，在掠入射法测量时选用了4条谱线。汞灯中的黄光、绿光、紫光等谱线的位置均比较准确，因此实验中汞灯的谱线被全部用来实现测量。最小偏向角法选择了12条谱线。

同样的选取谱线的方法，使用掠入射法时选择了10条谱线。相比最小偏向角法少测了2条光线的主要原因在于，采用掠入射法观测时，由于要找到不同波长光形成亮点且刚好不消失的位置，使得光点位置的判断比较困难，由于存在一些亮度较低的光线，其形成的亮点将会比较模糊，对于判断消失的位置产生较大的不确定性，因此，测量中将这些不能确定位置的光线予以忽略，最终获取了10条能较准确确定位置的光点。

图6 掠入射法氦灯色散光谱

3.2 两种方法所测数据处理

实验测量中，由于使用了氢灯、氦灯、钠灯和汞灯四种不同的光源，其中能够准确确定位置和波长的谱线分别进行测量，获取的测量结果要比使用单一光源测量的结果更为精确，且测量数据点相对也比较多，在一定程度上保证了实验结果的可靠性。

由选定谱线所测得的最小偏向角或最小出射角，根据式(2)(3)可以获取三棱镜对各个波长光的折射率。两种方法所得实验数据以及折射率如表1所示。由表1可以看出，三棱镜对于可见光波长的折射率数值在1.66～1.72之间，不同波长的可见光折射率差别较小。不同波长的可见光折射率差异较小，由掠入射法求出的折射率与由最小偏向角法求得的折射率结果极为相近，相对误差的绝对值均小于0.12%，依据两种测量方法所获得的结果可以进行相互的校验，从而证明这两种方法均是研究三棱镜色散特性较为精确的实验方法。

表1 几种光源谱线最小偏向角折射率对应表

图8 最小偏向角法关系曲线二次拟合比较图

图7 两种方法所得数据散点图对比

其中R2=0.999 2，拟合度较高，由此获得折射率与光线波长间的经验公式如下

(5)

使用掠入射法所得数据进行同样的处理

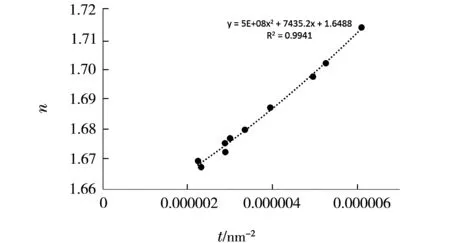
图9 掠入射法关系曲线二次拟合比较图

所得R2=0.994 1，拟合度较高，由此获取折射率与光线波长间的经验公式如下

(6)

由式(5)和式(6)可知，这两种方法获取的色散规律均符合正常色散，与柯西色散公式相一致。且能由图中看出单色光的波长越小，折射率越大，三棱镜对于该光的折射效果越明显。从两者二次多项式拟合度的差异可以进一步证明，最小偏向角法所得色散规律与柯西色散公式吻合度相对更高，其测量结果准确度也更高。这与前面的实验结果分析中由于掠入射法在判断形成亮点位置的不确定性导致位置采集的随机误差较高，其测量结果精度相对较低的结论相一致。

接下来对两种实验数据进行n-t关系曲线的一次多项式拟合，得到拟合的方差。其中掠入射法所得R2=0.992 1，拟合度较高，但略低于二次拟合结果的拟合度；最小偏向角法所得R2=0.998 2，拟合度高于掠入射法的一次拟合度，同样拟合度略低于其二次拟合结果的拟合度。

3.3 最小偏向角法和掠入射法对比

从选定测量光线位置的难易程度及不确定性程度方面来看，最小偏向角法选定每条光线的拐点位置相对比较确定且较容易获取，使得测量最小偏向角大小比较方便且准确度较高；掠入射法寻找的位置为光线恰好缩为短细线且刚好肉眼能够分辨的位置，由于人眼对于光的敏感程度因为实验人员的不同会存在较大差异，而且当光变为短细线时，其亮度将会较低，这为将光线放入视野的中心增加了一定的难度，这是导致掠入射法相对最小偏向角法测量精度降低的主要原因。

最小偏向角法的测量难度较低，所得结果准确度以及对于光线的分辨率相对更高，为一种更为有效且值得推广使用的方法；人眼分辨率及操作偶然误差成为影响掠入射法测量精度的主要因素，但作为分光计调节拓展性实验内容，在研究光谱色散特性方面，仍然是具有较好应用价值测量内容。

4 结 语