升压法测量静态蒸发率理论分析及试验研究

杨 刚，谭 粤，李 蔚，夏 莉

（广东省特种设备检测研究院，广东 佛山 528000）

0 引言

低温绝热气瓶作为一种储运低温液体的特种设备，具有充满率大、使用方便等特点，被广泛的应用在工业生产、医疗和能源储运等行业。低温绝热气瓶由外壳、内胆及绝热夹层组成。TSG R0006-2014《气瓶安全技术监察规程》[1]规定，低温绝热气瓶宜每3年进行一次绝热性能相关检验，静态蒸发率为我国目前衡量该类设备绝热性能的唯一指标。现行的检验原理及操作方法参照GB/T 18443.5-2010《真空绝热深冷设备性能试验方法第5部分：静态蒸发率测量》[2]执行。该标准规定了称重法和流量计法两种测量方法，但由于车载气瓶自身工作条件的限制，上述两种方法已不能满足部分低温绝热气瓶的实际使用工况，主要体现在：（1）车载低温气瓶安装空间紧凑，有时无法安装流量计等测试装置；（2）称重法测量必须拆装气瓶，费工费力；（3）两种方法测试周期都较长（大于24 h），很难满足如公交车等的实际使用要求。为了提高检测效率、降低企业成本、尽可能减少因检验对车辆运行带来的不良影响，本文提出了用升压法测量静态蒸发率的方案。

升压法是一种适于低温绝热气瓶在工作状态下、免工质更换、快速测量静态蒸发率的在线检测方法。其原理为气瓶在密闭状态下，外界热量透过绝热层进入内部介质中，使得低温液体吸热气化，瓶内压力升高，通过对漏热量进行理论计算进而表征静态蒸发率。已有学者进行了相关研究，提出用24 h自升压法测量车用液化天然气（LNG）气瓶[3]，并给出了相应的判定经验值[4-5]，以此来快速甄别气瓶的静态蒸发率是否合格。对于升压过程机制的研究，部分学者认为，升压过程中的瓶内压力可直接作为饱和状态的压力来计算[6-7]，但计算结果均远高于实际蒸发量。

本文在上述背景下，通过理论分析建立升压法测量静态蒸发率计算公式，并对升压法测量过程的影响参数进行对比研究，验证结果的准确性，为升压法测量的进一步推广应用及理论分析提供参考。

1 理论分析与公式推导

1.1 介质热力性质分析

根据《低温工程技术·数据卷》[8]流体介质压焓示意图可知，气瓶在自然升压过程中，气液两相的物性都会随着压力的变化而变化，如图1所示。气瓶在初始充满状态下静置升压过程中，两相介质均发生连续物性变化。相同压力下最突出的变化就是气液两相均会产生密度差异，恒定密度由绿色线给出。分析表明，气相空间与液相空间均会形成一个温度场，且温度梯度明显，气相空间主要沿轴向分布，由气液两相界面到气相空间顶部的温度递增；液相空间内由于瓶壁为主要热边界，介质吸收外界热量温度升高、密度减小，由此产生边界层流动（沿瓶壁向上），直至介质产生翻滚形成密度分层[9-10]。液相空间受介质翻滚与密度分层的影响，在介质中心线上会受到中心射流的冲击和卷携作用，导致中心部位的密度梯度比其他部位的密度梯度小[11]，且宏观上液相温度场以轴心线向外，温度沿径向递增分布。由此可见，气瓶在自增压过程中气相空间处于非均匀饱和状态，因此用理论计算气瓶的吸（漏）热量时，须将瓶内的非均匀饱和状态“摇匀”至完全饱和状态。

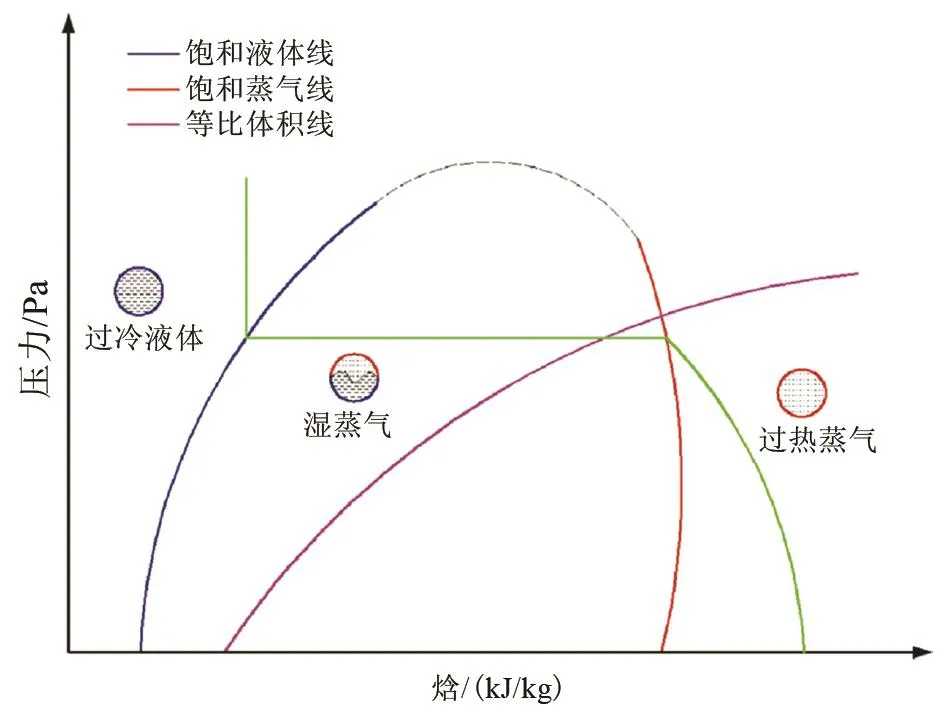
图1 流体介质压焓示意图Fig.1 Pressure-enthalpy schematic diagram of fluid medium

1.2 公式推导

GB/T 18443.5-2010[2]规定的称重法与流量计法的热力学模型为开口系统，与外界进行热交换的介质包括气液两相，依据工程热力学能量守恒定律[12]，其能量平衡方程为：总吸热量=液相吸热+气相吸热；而升压法的热力学模型为闭口系统，能量平衡方程为：总吸热量=最终状态-初始状态。鉴于两者总吸热量几乎相等，以此来推导升压法测量静态蒸发率计算公式。

被测气瓶充装试验介质至额定充满率，静置达到热平衡后，首先测量放空阀管路进气口平均温度T′，然后进行初始称重，由于气瓶处于额定充满率时，气相空间很小，因此气相部分的质量可以忽略，介质的总质量可看作是液相介质的质量，得到：

式中：m0为初始状态下的总质量，kg；mls为初始状态下液体的质量，kg。

称重完成后，气瓶内的测试介质处于初始饱和状态（101.325 kPa），对应得到初始饱和状态方程：

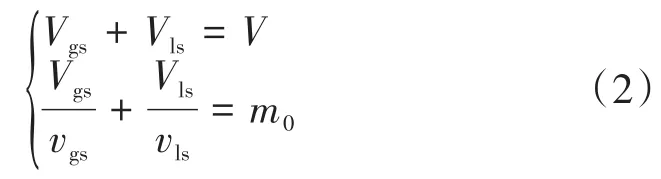
式中：V为气瓶的有效容积，m3；Vgs为初始状态下气相空间的体积，m3；Vls为初始状态下液相空间的体积，m3；vgs为-初始状态下气相的比体积，m3/kg；vls为初始状态下液相的比体积，m3/kg。

之后，将压力传感器连接至放空阀上，保持放空阀开启且关闭其他阀门，使整个气瓶内部进行自然升压，整个过程试验介质无损耗。自然升压结束后，摇晃被测气瓶，使得试验介质的气液两相处于最终的饱和状态，此过程会伴随气瓶内部压力下降，记录压力下降的最低值为最终饱和状态压力，由此得到最终饱和状态方程：

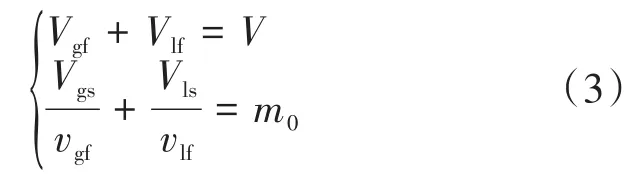
式中：Vgf为最终状态下气相空间的体积，m3；Vlf为最终状态下液相空间的体积，m3；vgf为最终状态下气相的比体积，m3/kg；vlf为最终状态下液相的比体积，m3/kg。

依据热力学闭口系统的能量平衡方程，得出自然升压过程的漏热量计算公式：

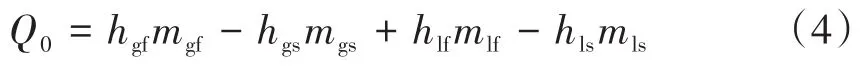
式中：Q0为测试周期内的漏热量，kJ；hgs为初始状态下气相的比焓，kJ/kg；mgs为初始状态下气相的质量，kg；hls为初始状态下液相的比焓，kJ/kg；mls为初始状态下液相的质量，kg；hgf为最终状态下气相的比焓，kJ/kg；mgf为最终状态下气相的质量，kg；hlf为最终状态下液相的比焓，kg；mlf为最终状态下液相的质量，kJ/kg。

根据能量守恒定律，得：

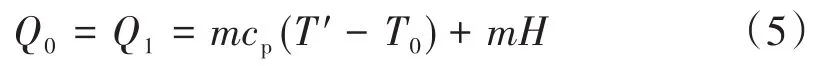
式中：Q1为称重法/流量计法计算的漏热量，kJ；m为蒸发液体质量，kg；cp为气体在T′温度、给定压力下的定压比热容，kJ/（kg·K）；T′为放空阀管路进气口测量温度平均值，K；T0为101.325 kPa（1个标准大气压）下饱和液体的温度，K；H为101.325 kPa下饱和液体的气化潜热，kJ/kg。

因此，

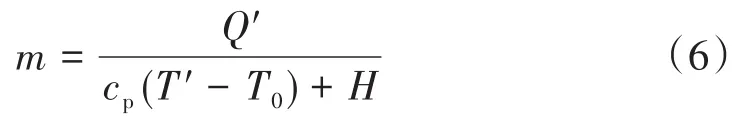
最终，日静态蒸发率为：

式中：α0为日静态蒸发率测量值，%/d；ρ为101.325 kPa下饱和液体的气化潜热，kg/m3；V为被检件的有效容积，m3；n为测试时间，h。

以上升压法测量静态蒸发率的全部推导公式是基于气液两相介质始末状态均处于饱和态得出的，为升压法测量的应用提供了一定的理论计算依据，并与现行标准规定的测量方法形成对应关系。

2 试验研究

2.1 不同充满率对自然升压过程的影响

试验选取国内某品牌在用的196 L焊接绝热气瓶为研究对象，试验介质为液氮，测试充满率为95%、90%、80%、70%、60%、50%（充满率小于50%的对比分析对静态蒸发率测量无实用性意义），自然升压时间为24 h，结果如图2所示。

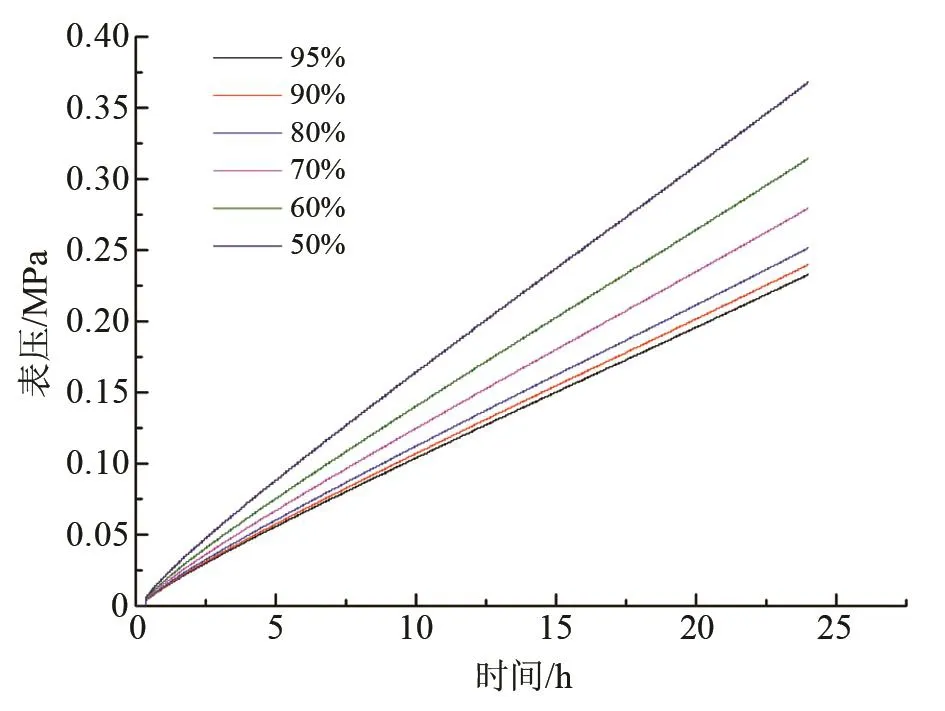
图2 不同充满率下自然升压曲线对比Fig.2 Comparison of natural pressure rise curves under dif‐ferent filling rates

由图2可知：（1）气瓶在不同充满率下24 h内的自然升压过程均呈线性变化，近似为正比例函数；（2）初始充满率越高自然升压速率越慢（曲线斜率越小），当充满率小于80%时，自然升压速率差值逐渐增大；当充满率大于等于80%时，升压速率相差不大，当以90%充满率为基准时，此充满区间内的升压曲线斜率相差在5%以内；（3）0～3 h内升压速率不稳定，整体偏高，因此自然升压过程以3 h以后的数据为准。

2.2 不同容积对自然升压过程的影响

试验分别选取国内某品牌175 L、250 L、450 L焊接绝热气瓶和150 L、330 L、450 L汽车用LNG气瓶为测试对象，试验介质为液氮且均在额定充满率下进行对比测试，自然升压时间为24 h，如图3所示。

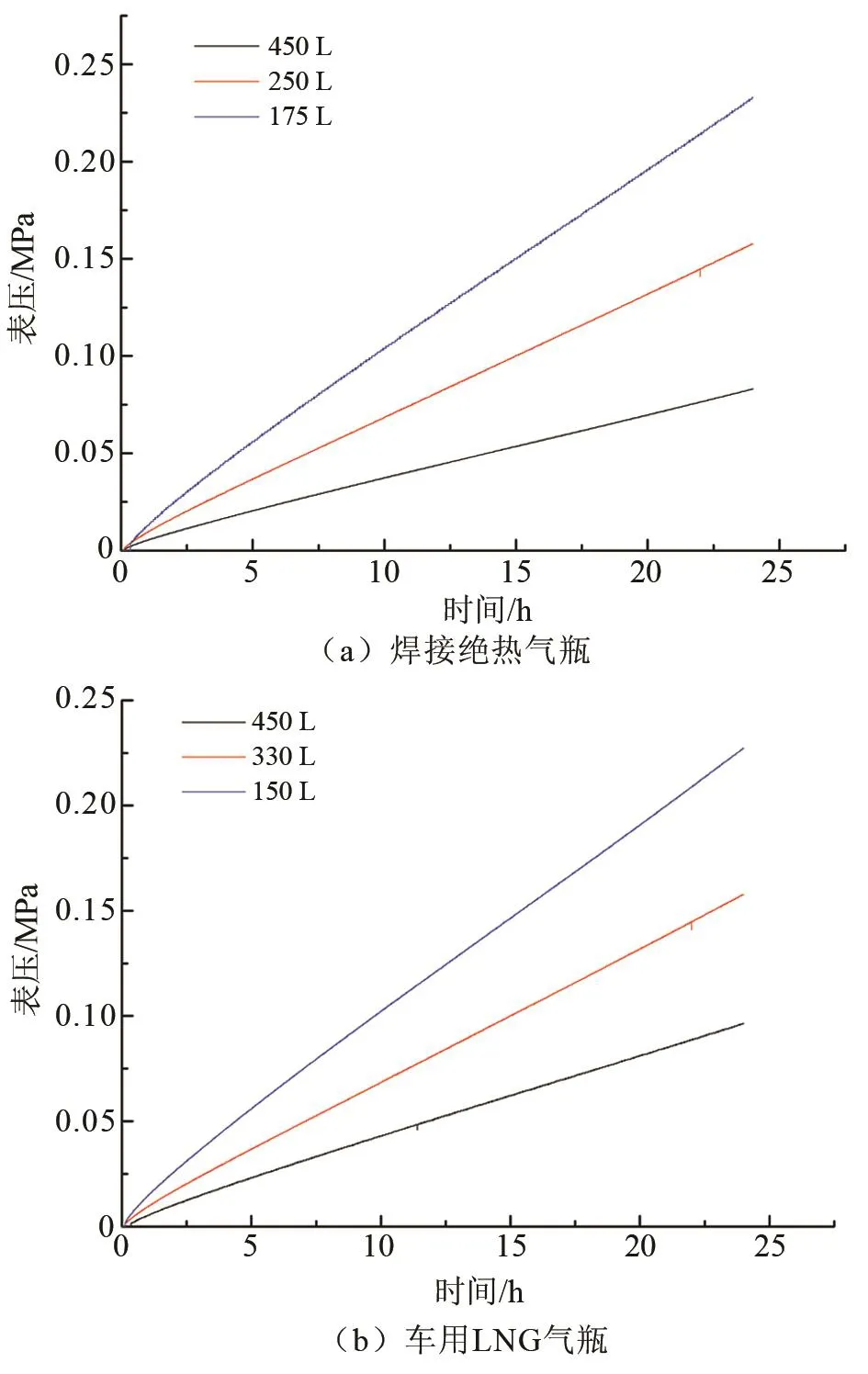
图3 不同容积下自然升压曲线对比Fig.3 Comparison of natural pressure rise curves under different volumes

由图3可知：（1）在额定充满率下，不同容积的低温绝热气瓶在24 h的自然升压过程中均呈线性变化，近似为正比例函数曲线；（2）低温绝热气瓶容积越小，介质总冷量就越少，相同的热传递条件下介质状态变化会更大，因此其宏观呈现升压速率较高（曲线斜率较大）；（3）由于结构设计原因，相同容积的车用LNG气瓶较焊接绝热气瓶的升压速率快、静态蒸发率高。

2.3 试验设计

基于上述理论分析及公式推导，制定出本试验工艺并设计定制相应的低温绝热试验瓶，该试验瓶内设置了若干热电偶用于测量瓶内气液两相的温度变化过程以及放空阀管路进气口测量温度平均值T′，瓶外配备了压力传感器以及数据采集、处理系统，如图4所示。

图4 升压法测量静态蒸发率装置示意图Fig.4 Schematic diagram of device for measuring static evaporation rate by pressure rise method

2.4 测温点的温度变化

选取液氮为试验介质，试验瓶处于放空阀打开状态，热电偶连续记录瓶内液相空间和气相空间的温度变化过程，结果如图5所示。

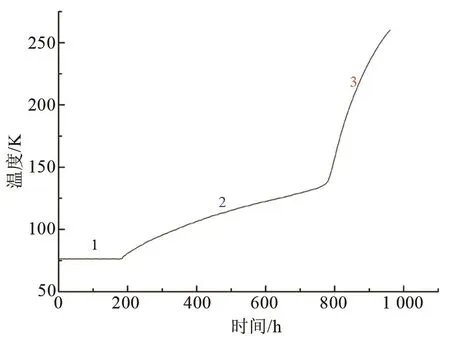
图5 某一测温点的温度变化曲线Fig.5 Temperature change curve of a temperature measuring point

由图5可知，整个温度变化曲线分为3个阶段：第1阶段，热电偶一直处于液相空间，所以该阶段温度始终处于77 K；第2阶段，由于液氮不断蒸发，热电偶所处环境逐渐由液相空间变换为气相空间，且该阶段“温度-时间”曲线大致呈线性变化，升温速度为1～3 K/d；第3阶段，随着液氮量不断减少，瓶内总冷量降低，尤其在液位低至下封头高度以下时，气相空间升温速率骤增。

2.5 最终饱和状态压力点获取

升压法测量是基于被测气瓶处于热力学模型闭口状态下的自然升压。试验选取上述定制气瓶，公称容积175 L，试验介质为液氮，分别测试其在额定充满率下1 h、2 h、3 h、4 h、5 h、6 h、7 h、10 h、13 h、16 h、20 h、24 h内的自然升压情况以及通过“摇晃”获得的完全饱和状态压力点，结果如图6、图7所示。

由图6可知，升压法研究过程中往往存在一个误区，即认为气瓶的自然升压过程中气液两相介质始终处于“饱和态”。从微观层面看，将单个气体分子或液体分子视作分析单元，每个单元在升压过程中均处于物性连续变化状态，包括：温度、密度、焓值等，因此直接将此状态（仅压力已知）下对应的饱和态物性参数带入漏热量计算公式时会产生巨大误差。通过“摇晃”操作，使得原来气液两相所处的非均匀饱和状态趋于均匀饱和，此时整体压力值会骤降，呈现出图6所示的曲线。图7中不同测试时间对应的饱和状态点形成一条介质饱和态升压曲线，0～5 h的升压速率高于6～24 h，主要形成原因有：（1）摇晃做功可能对短时间的升压过程影响较明显；（2）颈管部位引入的热流占气瓶总热流的比例可达一半以上[13]，摇晃过程中气相空间与颈管换热加剧，导致最终饱和状态点压力偏高。

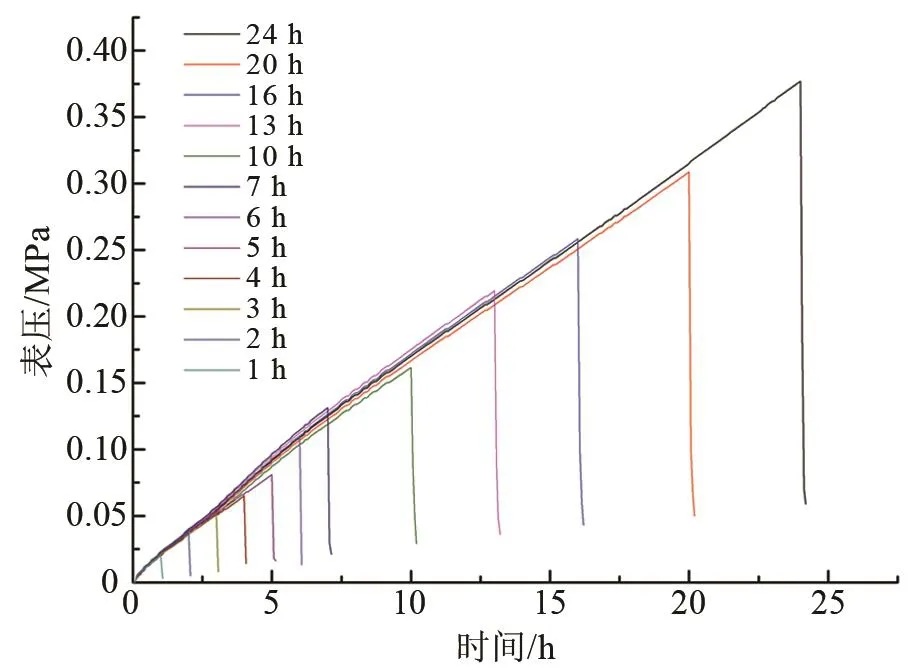
图6 不同测试时间下自然升压及对应摇晃曲线Fig.6 Natural pressure rise and corresponding shaking curves under different test times

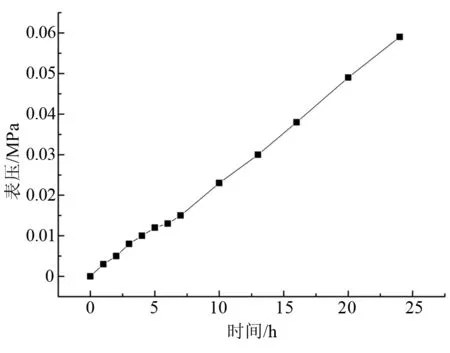
图7 不同测试时间下饱和状态升压曲线Fig.7 Saturation state point curve at different test times

2.6 结果分析

将图7中各测试时间所对应的最终饱和态压力值代入NIST REFPROP 9.1[14]介质物性数据库，获得气液两相对应的比体积、比焓等参数，连同试验测得的175 L试验瓶放空阀管路进气口温度平均值T′=124.5 K一起代入式（1）～（8），求出升压法测量静态蒸发率结果。为了验证结果的准确性，将其与标准中规定的称重法/流量计法测量结果进行对比，如表1所列。由表1可知：（1）当升压法的测试时间小于6 h时，静态蒸发率测量结果比称重法和流量计法误差大，但随着测试时间的延长相对误差呈逐渐减小趋势。（2）当测试时间在6～24 h时，升压法测量静态蒸发率结果 分 别 为 3.11%、3.06%、3.20%、3.13%、3.15%、3.15%、3.08%，比称重法和流量计法的测量结果最大相差0.09%，相对误差均小于3%。上述结果验证了理论分析的合理性及计算公式的准确性。（3）1～5 h测量存在较大误差的原因分析：1）初始称重时量器自身精度不够高；2）摇晃操作时增加额外换热面积，很小的气化增量即可引起对应饱和压力的增高。

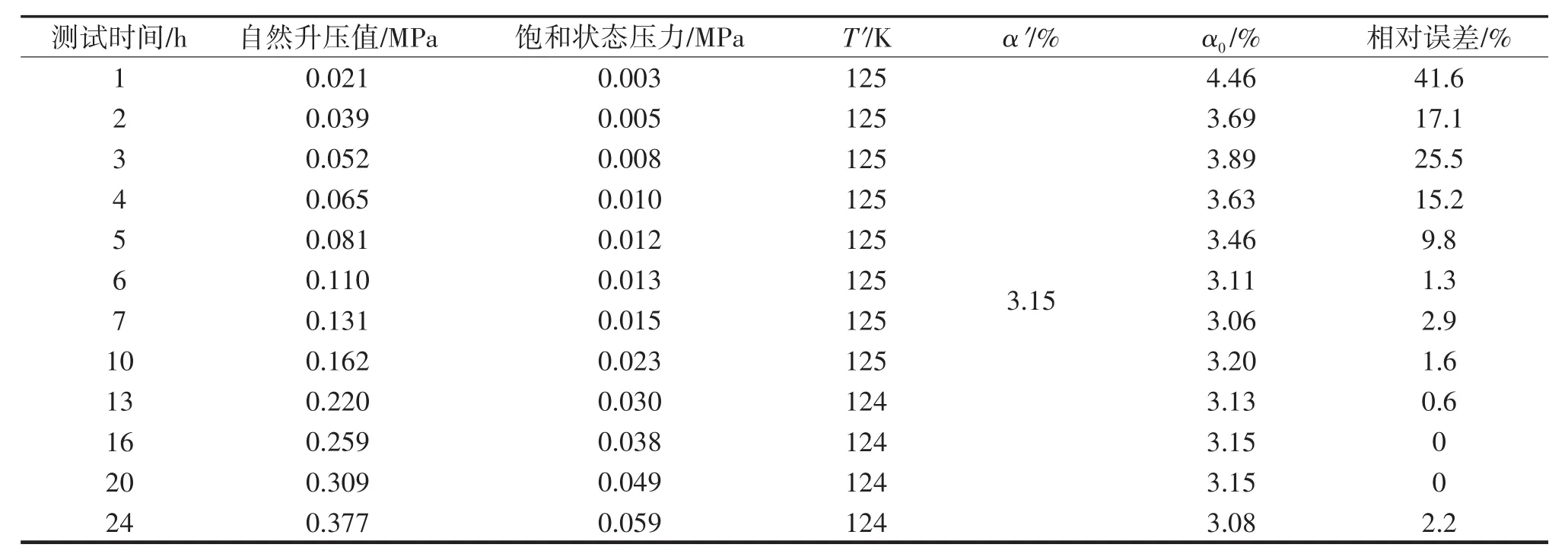
表1 升压法与称重法/流量计法静态蒸发率测量结果对比Tab.1 Comparison of static evaporation rate measuremen tresults between pressure rise method and weighing method/flowmeter method

3 结论

升压法测量静态蒸发率能够有效地弥补现行方法的不足，本文对升压法进行了公式推导和试验验证，得到如下结论：

（1）自然升压过程中气液两相介质物性均在湿蒸气两相区变化活动，气相空间温度由气液两相界面到气相空间顶部递增；液相空间传热过程引起介质翻滚与密度分层，宏观上液相温度场以轴心线向外，温度沿径向递增分布，且中心部位的密度梯度比其他部位的密度梯度小。

（2）基于热力学能量守恒定律，分析了开口系统与闭口系统的传热机制，进而推导得出升压法测量的计算公式。

（3）通过低温绝热气瓶的自然升压过程得到一个共性的自然规律：“压力-时间”曲线呈线性变化且近似为正比例函数。升压速率受充满率和有效容积的影响：1）初始充满率越高自然升压速率越低，当充满率小于80%时，自然升压速率逐渐增大；当充满率大于等于80%时，升压速率相差不大；当以90%充满率为基准时，此充满区间内的升压曲线斜率相差在5%以内；2）有效容积越小，介质总冷量越少，相同的热传递条件下介质状态变化会更大，因此升压速率较高。

（4）当升压法测试时间小于6 h时，静态蒸发率测量结果比称重法和流量计法误差大，但随着测试时间的延长相对误差呈逐渐减小趋势；当测试时间在6～24 h时，升压法测量结果较称重法和流量计法的误差均小于3%，不同方法间测试结果满足一致性要求。基于上述试验结果，升压法的理论分析合理性及计算公式准确性得以验证。