磁流变弹性体基拓扑声子晶体弹性波传输可调性研究*

李潘玉，游世辉,2，李 维，张圣东,3，曾宪任

(1. 湘潭大学 土木工程与力学学院，湖南 湘潭 411105； 2. 枣庄学院 机电工程学院，山东 枣庄 277000；3. 九江学院 机械与材料工程学院，江西 九江 332005)

0 引 言

量子霍尔效应[1]、量子自旋霍尔效应[2-3]和拓扑绝缘层[4-5]的发现为经典波的拓扑性质的探索奠定了基础。弹性波作为经典波之一，发展了声学超材料[6-7]、超表面[8]等许多人工的周期结构以达到对弹性波传播的控制与引导。随着基于量子自旋霍尔效应的拓扑概念的引入，声学超材料在弹性波的精确控制[8]、声学拓扑绝缘体[9]、声学拓扑隔离器[10]、拓扑谷传输[11]等方面的探索引起了广大学者的高度关注，这些拓扑边界保护特性不受边界缺陷和材料杂质的影响。形成拓扑边界的一种方法是引入有源分量或外场等打破时间反演对称性[12-14]，或者旋转陀螺仪打破时间反演对称性[15]；另外一种是类比量子自旋霍尔效应实现拓扑边界态[16-18]，Lu等[11]，利用量子谷霍尔效应通过打破空间对称性来实现声的拓扑谷传输。2015年，陈子亭课题组[19]利用能带反转和拓扑相变，首次在声学系统中引入拓扑概念，构造了结构中心截面镜像对称的圆管状声子晶体，并通过改变结构参数来实现禁带的拓扑性质的变化，发现了在两种不同拓扑性能的声子晶体组合的边界处有界面态的存在；同年，德克萨斯大学奥斯汀分校 Wang Z课题组通过打破超材料板的空间反演对称性，实现了对称和反对称兰姆波二重简并能带打开—闭合—再打开的能带反转的拓扑相变过程[20-21]；2016年，刘正猷课题组首次在基于声子晶体研究领域中引入电子系统中的谷态的概念，通过旋转具有C3v对称性的元胞来构建谷自旋，达到实现量子谷自旋霍尔效应类比[22-23]；同年，陈延峰课题组构造了钢柱—空气声子晶体，找到了Γ点处的偶然双狄拉克点并通过调整钢柱半径实现了能带反转[24]；2017年，刘晓俊课题组理论证明了在不加流速背景下通过声子晶体构造声学赝自旋偶极子和四极子，实现了弹性波的拓扑传输[17]；同年，Vila Javier和Pal Raj Kumar 设计了二维弹性六角晶格。采用模拟和实验的方法，通过在不同节点上引入质量差，成功地打开了位于布里渊区中 K 点的狄拉克点，并观测到了不同构型的元胞界面处的边界态[25]。

然而传统的声学超材料在结构设计完成后不具有带隙可调的性质，因此无法满足不同工作环境的要求，限制了其应用范围。随着对超材料的研究更加深入，带隙可调的声学超材料成为了研究者们热衷研究方向。Goffaux和 Vigneron通过旋转二维声子晶体中的正方形散射体的角度对带隙的宽度进行调控[26]；Wang和Kushwaha[27]通过调节方柱形波导的方柱几何尺寸来调节带隙；Bertoldi等[28]通过改变晶格与散射体形状来调节带隙；Zhou 等[29]提出了多包覆层局域共振单元结构,并讨论了包覆层数量及厚度对带隙的影响。以上方法的局限性在于声学超材料制备完成后无法对带隙实现主动调控，智能材料的引入实现了对声学超材料参数的主动调控。Yeh[30]以电流变弹(Electrorheological Elastomer)材料作为基体，环氧树脂作为散射体组成二维声子晶体，通过研究发现外加电场对带隙的宽度和位置产生影响；Xiao等[31]设计了薄膜声学超材料；用薄膜上电极与另一侧网状电极构成电容器，通过调节电容两端电压改变薄膜的共振频率和相位从而实现弹性波传输过程中带隙的主动调节；磁流变弹(Magnetorheological Elastomers,MREs)性体作为一种智能材料，可以通过改变外加磁场的方式调控材料的力学性能，并具有响应快、可逆性好、可控能力强等特点[32-33]。Chen等[34]将MREs薄膜覆盖于铝制环上设计了一种磁—声超材料，Xu 等[35]使用MREs 包覆层共振单元实现了三维局域共振声学超材料的设计，两者均可以通过改变外部磁场调节声学超材料的频率带隙；刘少刚等[36]使用MREs设计了单、双包覆层的声子晶体元胞结构，也可通过磁场改变调节带隙以及传输谱特性。

虽然研究者们在声学拓扑绝缘体和声子晶体带隙的主动调控方面都做出了深入的研究并取得了大量的成果，但是在弹性波拓扑通道的非接触式智能调控的研究却比较少。以往的研究以重芯体分布在基体材料中组成声子晶体，本文利用磁流变弹性体可以通过外加磁场连续控制其力学性能的特点，在前人研究的基础上，以硅胶作为基体，磁流变弹性体材料包覆金属钨作为散射体设计了一种二维蜂窝状声学智能超材料，通过打破元胞的空间对称性并引入质量差的方式来实现能带反转，结合基于声子晶体的类似量子霍尔效应的赝自旋态，实现了弹性波的拓扑传输绝通道的构造；并通过外加磁场调节包覆层MREs的剪切模量等力学参数，实现了拓扑通道可传输频率大小及范围的智能调控，此外还讨论了芯体材料密度对拓扑通道传输频率的影响。本文的研究可以为新型智能材料的研究及弹性波的精确引导等提供相应的参考。

1 模型与方法

1.1 二维声学超材料结构设计

通过将磁流变弹性体圆环包覆的金属圆柱以蜂窝状晶格嵌入硅胶基体中构造声学超材料的原始模型如图1(a)所示，晶格常数a=1 μm，芯体的半径r1=0.185 μm，包覆层外径r2=0.25 μm，对应的能带结构为图1(a)。通过元胞几何参数的调节找到了受元胞结构和晶格对称性保护的K点必然简并点(图1(a)中圆形标记位置)。通过打破晶格空间对称性[20-21]和引入质量差的方法[25]调节左边MREs环包覆层厚度并去除里面的芯体，当左边MREs包覆层内环半径为r3=0.2 μm时(如图1(b))，k点简并点明显打开并在第8和第9两条能带之间产生了完全禁带；同时，第3能带与第4能带之间也产生了局域共振型禁带。本文主要研究对象为8、9条能带所构成的禁带。

图1 声学超材料元胞结构Fig 1 Acoustic metamaterial protocell structure

本文使用的硅橡胶材料参数为：密度ρs=800 kg/m3,拉梅常数λ=24.67 MPa,μ=0.772 MPa，MREs材料计算采用经典的磁偶极子模型，橡胶和铁粉颗粒密度分别为密度定义为ρr=1.2×103kg/m3,ρFe=7.89×103kg/m3，泊松比取0.47[37]，外磁场作用下MREs材料剪切模量按照式(1)变化[38-39]。

(1)

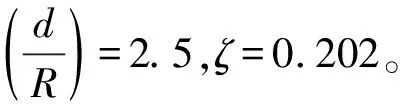
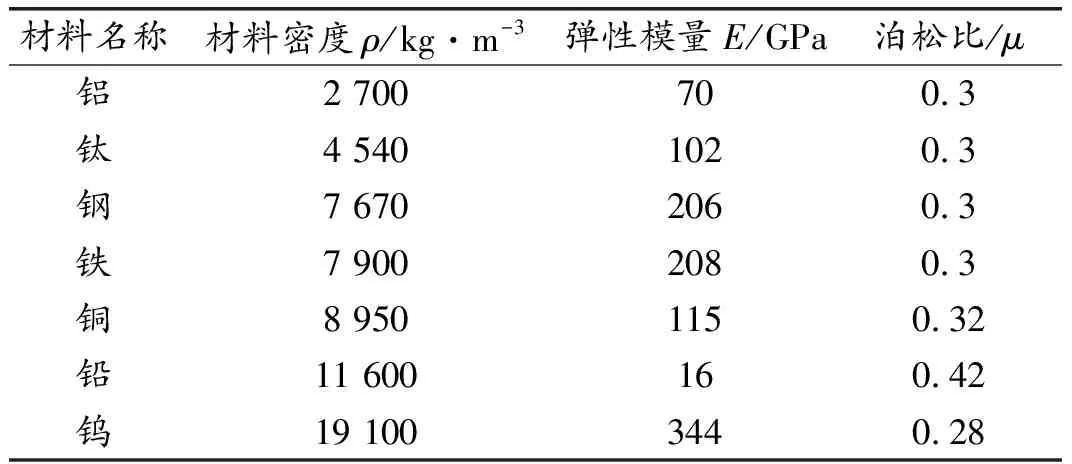
表1 芯体材料力学参数

1.2 平面波展开法与有限元法

平面波展开法利用晶体结构的周期性，将弹性系数和密度等参数按照傅里叶级数展开，结合Bloch定理，将弹性波波动方程在倒矢空间以平面波叠加形式展开，将波动方程转化为求解本征值问题，从而得到能带结构[40]。平面波展开法在计算固/固声子晶体能带结构已经非常成熟，具体求解可以参考文献[41]，在2.4节中，本文基于MATLAB编程使用平面波展开法来计算禁带上下边界频率并与有限元法计算结果进行验证，结果一致。

有限元法基于集中质量法思想[42]，将连续介质中的质量集中到有限的点或者面上，将无限自由度转化为有限自由度求解。能带结构的计算收敛性不受声子晶体中不同介质弹性常数差的影响，在计算大弹性常数差声子晶体能带结构拥有比平面波展开法等其他方法更高的计算精度和较好的收敛性。本文使用多物理场仿真软件COMSOL Multiphysics©对声学超材料的能带结构进行计算以及对拓扑边界态的频域传输现象进行仿真。为了在COMSOL Multiphysics©计算元胞能带过程更方便的进行参数化扫描，定义参数k范围为0～3，将0～1定义为覆盖不可约布里渊区M-K边缘的波数；1～2定义为覆盖K-Γ边缘的波数；2～3定义为Γ-M边缘的波数。

2 计算结果与讨论

2.1 元胞能带反转和拓扑相变

通过打破晶格的空间对称性并引入质量差的方法，改变左边包覆层半径并去除芯体材料的质量(第一次简并点打开，图2)与改变右边包覆层半径并去除芯体质量(第二次简并点打开，图3)作为两种相反的调节方式，使k点必然简并狄拉克点从打开—闭合—打开并产生了禁带，并且在此过程中第8条能带与第9条能带发生了能带反转。图2(a)为第一次简并点打开对应的k=1时的高频能带元胞位移和能流图，可以看出位移和能流整体呈现旋涡状，具有顺时针方向的手性；图2(b)对应的是第一次简并点打开k=1时低频能带的位移和能流图，可以看出位移和能流表现出逆时针的手性。图3为第二次简并点打开对应的能带结构图和低频能带与高频能带对应的位移与能流图，可以看出，对比图2位移与能流都发生了相反的变化，低频能带具有顺时针的手性，而高频能带表现出逆时针手性；可以判断从k点简并点打开—闭合—打开，8、9能带之间发生了能带反转。

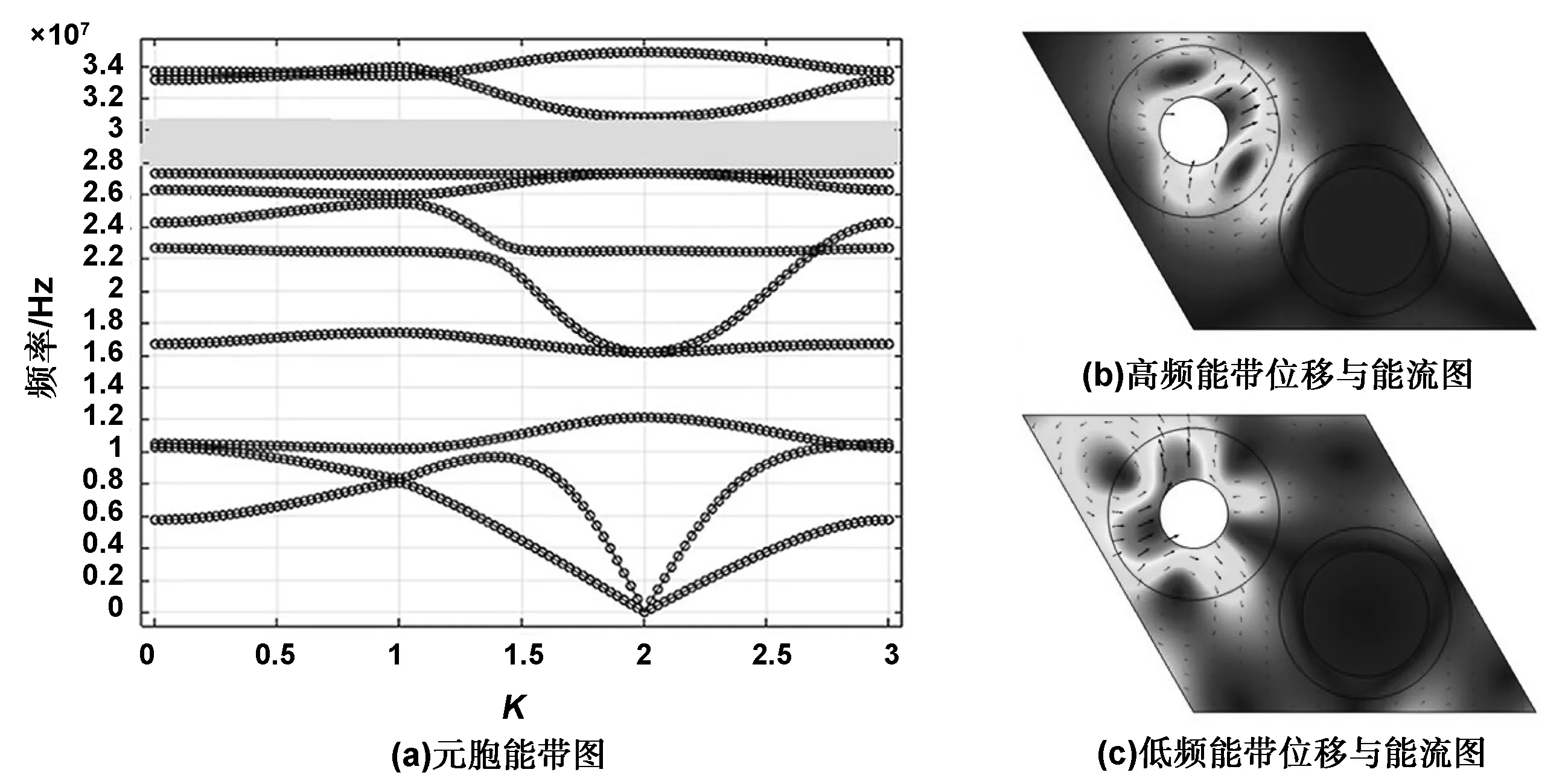
图2 第一次简并点打开Fig 2 The first degeneracy point opens

图3 第二次简并点打开Fig 3 The second degeneracy point opens

为了进一步证明8、9能带之间发生了能带反转，参考文献[43]引入了非零谷陈数的观点。通过k·p微扰法，可以得到有效哈密顿量:

(2)

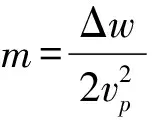
(3)

那么，可以通过积分布里渊半区的局部Berry曲率来计算能带的拓扑电荷：

(4)

k简并点打开时会产生谷赝自旋态，第一次简并点打开时自旋向上的陈数C↑=-1，自旋向下陈数C↓=1；第二次简并点打开时自旋向上的陈数C↑=1，自旋向下陈数C↓=-1，伴随着陈数的改变拓扑相位发生了转变，证明了上述两种不同的打开简并点的方法的确发生了能带反转。系统总陈数C=C↑+C↓=0，自旋陈数CS=±(C↑-C↓)=±1 ，可以为下面构造拓扑绝缘表面的传输通道作为理论基础。

2.2 超胞能带特性分析

定义改变左边包覆层半径并去除芯体材料的元胞为A型元胞,改变右边包覆层半径并去除芯体质量的元胞为B型元胞。接下来使用COMSOL Multiphysics© 中设置好相应的边界条件，分别对图4中A×10型超胞和A×5+B×5型杂化超胞的能带进行计算。由图5、6计算结果可以发现，AB杂化的超胞中在频率freq=2.7483×107Hz和freq=3.0359×107Hz时出现了拓扑边界态，而这种边界态并没有在A×10型超胞能带图中出现。进一步分析A×5+B×5型杂化超胞在拓扑边界处的模态(图7)，可以发现其响应主要局域在AB型元胞相接的部分，边上的响应被抑制，这就是超胞结构中存在的拓扑边界态；并且在freq=2.7483×107Hz边界模态处超胞受力方向为顺时针，freq=3.0359×107Hz边界模态处受力方向为逆时针，可以说明拓扑边界的传输具有方向性。

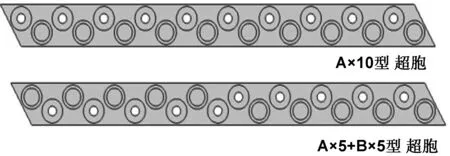
图4 型超胞结构图Fig 4 Supercell structure diagram

图5 A×10型超胞能带图Fig 5 Energy band diagram of supercell typeA×10

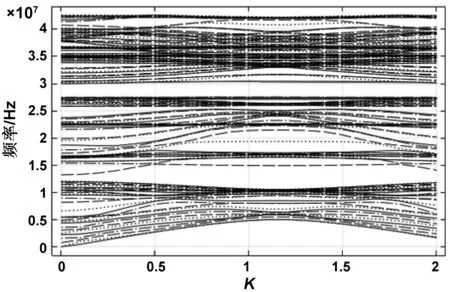
图6 A×5+B×5型超胞能带图Fig 6 Energy band diagram of supercell type A×5+B×5

图7 A×5+B×5型超胞拓扑边界处模态图Fig 7 The mode diagram at the topological boundary of type A supercell A×5+B×5

2.3 拓扑通道频域传输分析

利用COMSOL Multiphysics©软件的频域模块对有限大声学超材料板结构的弹性波传输进行仿真计算，首先设计如图8直线型拓扑传输通道，在边界处施加低反射边界条件，降低反射波对计算结果精确度的影响。在模型的一端施加线激励，通过计算发现，弹性波在拓扑边界范围内(2.7483×107～3.0359×107Hz)高效传输。由于拓扑边界态的局域作用，弹性波沿着设计的通道进行传输，在通道外没有能量的散射。通过计算直线型拓扑通道的透射谱(图10a)，可以进一步证实拓扑通道传输具有极低的能量损耗。为了进一步研究拓扑通道的性质，设计如图9的Z字型通道，通过在通道一侧施加线激励并计算，可以看出，弹性波的传输并不受拐角的影响，可以通过拐角继续向前传播并且在拐角处无能量泄露。同样计算Z字型拓扑通道的能量透射谱，结果如图10(b)，可以得出弹性波在拓扑通道内可以低损耗局域型高效传输。

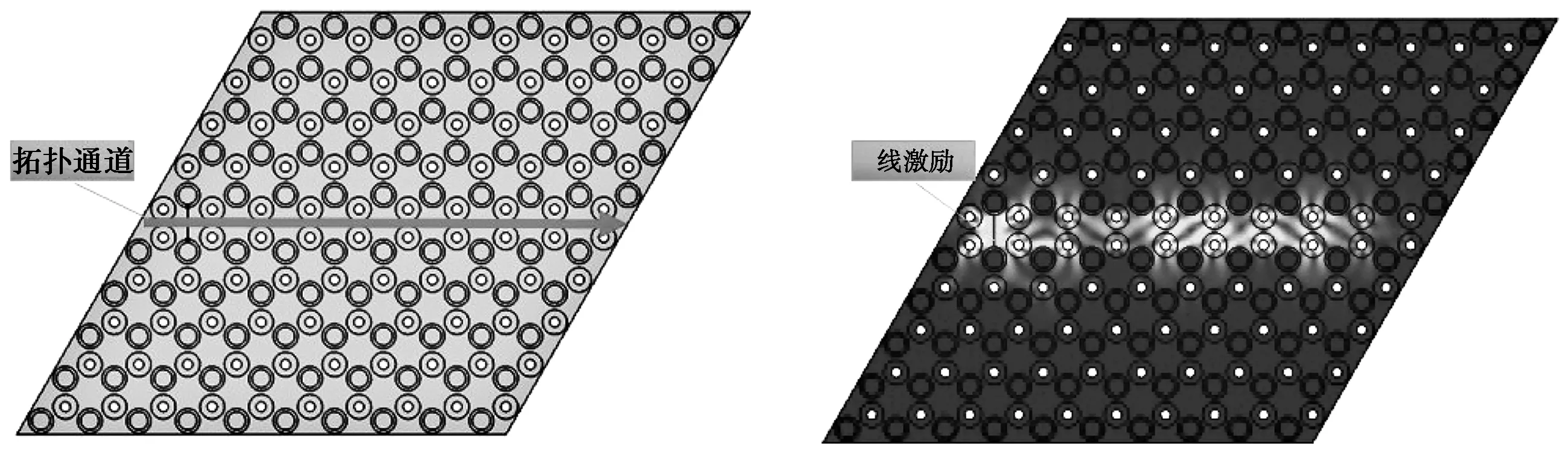
图8 直线型弹性波拓扑通道传输Fig 8 Transmission of linear elastic wave topology channel

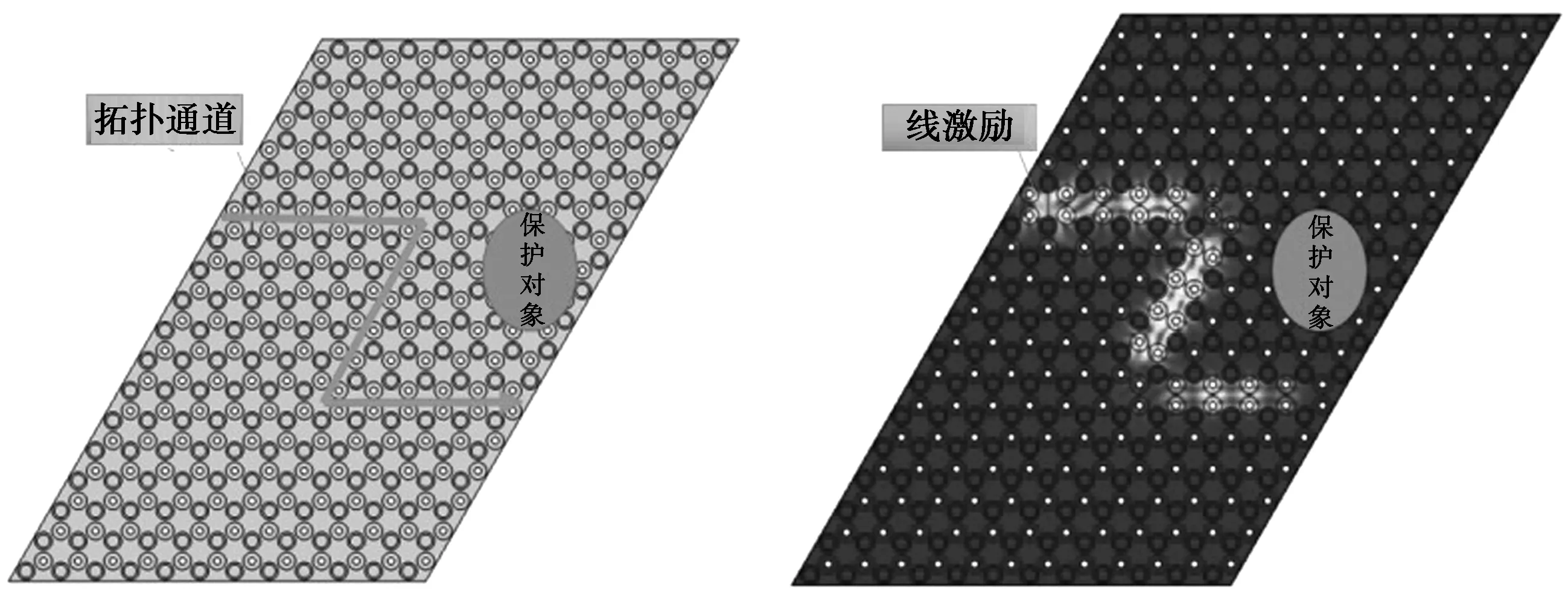
图9 Topological channel transmission of Z-shape elastic waveFig 9 Transmission of linear elastic wave topology channel

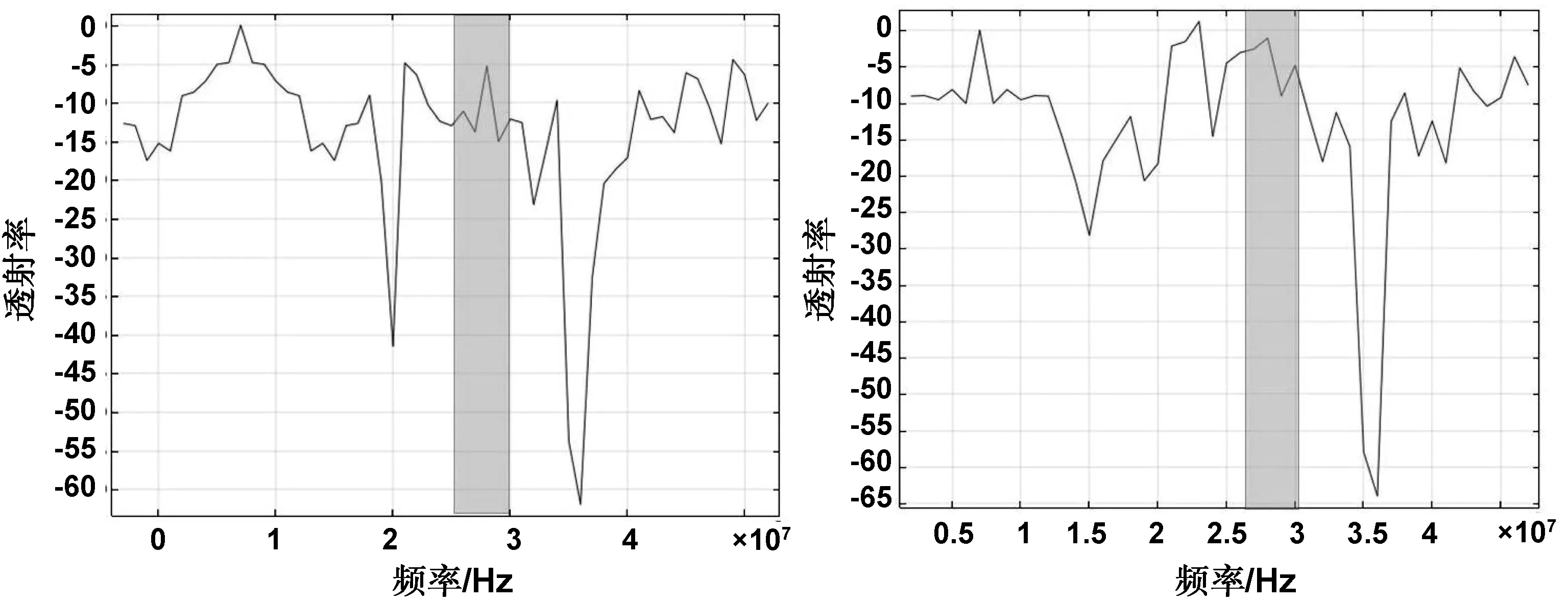
图10 (a)直线型弹性波拓扑传输通道透射谱 (b)Z字型弹性波拓扑通道传输透射谱Fig 10 Transmission spectrum of linear elastic wave topological transmission channel and transmission spectrum of Z-shaped elastic wave topology channel

通过在设计拓扑通道中引入缺陷如图11，来证明拓扑通道对于缺陷的鲁棒性。分别在直线通道和Z字型通道模型中加入缺陷并进行弹性波传输仿真计算和透射谱计算。结果与图8，9中没有引入缺陷时的透射率一致，表明即使在通道中引入缺陷也不影响弹性波在拓扑通道中的高效传播。

图11 (a)弹性波在引入缺陷的直线型拓扑通道传输位移图 (b)弹性波在引入缺陷的Z字型拓扑通道的传输位移图Fig 11 Displacement diagram of elastic wave propagation in a linear topological channel with a defect and transmission displacement Diagram of elastic wave in z-shaped topological channel with defect

拓扑通道对弹性波的精确引导可以根据实际要求设计相对应的路径，如图9中的Z字型路径可以巧妙的避开所要保护的对象，引导弹性波传播到别处可以进行能量回收二次利用；也可以根据需要设置弹性波高效率的传输到指定目标。

2.4 磁场强度与拓扑通道传输频率范围的关系

通过改变外加磁场强度可以调控磁流变包覆层的剪切模量等力学性能，从而调节拓扑通道传输的频率范围。本文计算了磁场从0～796 kA/m过程中基于磁流变弹性体声子晶体声学超材料的能带变化，定义第3、第4能带为第一阶带隙的下边界和上边界，第8、第9条能带为第二阶带隙的下边界和上边界；图12为构成禁带上下边界能带频率随着磁场增加的变化图，有限元法(集中质量法)与平面波展开法的计算结果基本一致，结果频率差均小于30 Hz，证明了计算结果的准确性。计算结果表明含有拓扑边界态的禁带(第二阶带隙)随着磁场强度的增加整体向高频移动，带隙下边界随着磁场的增大变化幅度比上边界大，因此带隙宽度随着磁场强度增大逐渐减小，当磁场强度为796 kA/m的时候，禁带关闭；计算结果与文献[44]所计算的变化趋势一致。通过计算0、159.2、318.4、636.8 kA/m磁场强度下拓扑传输通道的透射谱(图13)可以发现随着磁场强度的增加，透射谱的最大衰减频率也在整体向高频移动，进一步证明了第二阶带隙禁带随着磁场强度增大朝高频移动。第一阶带隙由于磁场强度增加，MREs材料的刚度增大，第一阶带隙整体向高频移动，由于刚度增大对带隙上边界的影响大于下边界，所以第一阶带隙的禁带宽度增加，与文献[45]中的质量弹簧模型计算的结果一致。因此可以通过调整外磁场的大小对拓扑通道的传输频率范围进行非接触式调控。

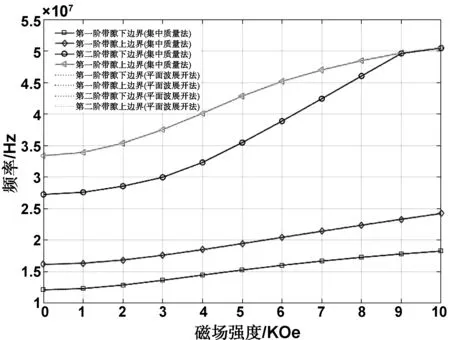
图12 禁带上下边界频率与磁场强度变化关系(有限元法与平面波展开法结果对比)Fig 12 Relation between upper and lower boundary frequencies of the forbidden band and magnetic field strength (comparison between results of Finite Element Method and Plane Wave Expansion method)

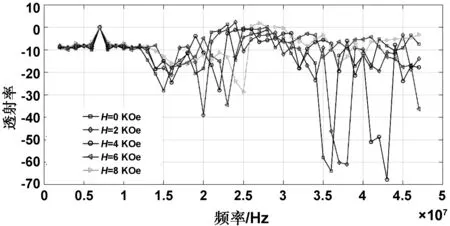
图13 不同磁场强度下拓扑通道的透射谱变化图Fig 13 Variation of transmission spectrum of topological channel under different magnetic field intensity

2.5 芯体密度与禁带频率范围的关系

分别使用表1中的材料作为声子晶体的芯体进行能带结构的计算，绘制禁带的上下边界频率与芯体密度的变化关系(图14)可以看出：第一阶带隙的随着芯体密度的增加，带隙下边界减小趋势比上边界快，因此禁带宽度增大，此变化趋势也与用文献[36]中质量弹簧模型一致。对于第二阶禁带，由于芯体密度增大，刚体共振频率朝低频移动且对上边界影响较大，导致带隙宽度变窄，带隙整体朝低频移动。基于此结论可以对于拓扑通道的传输频率实现被动调控。

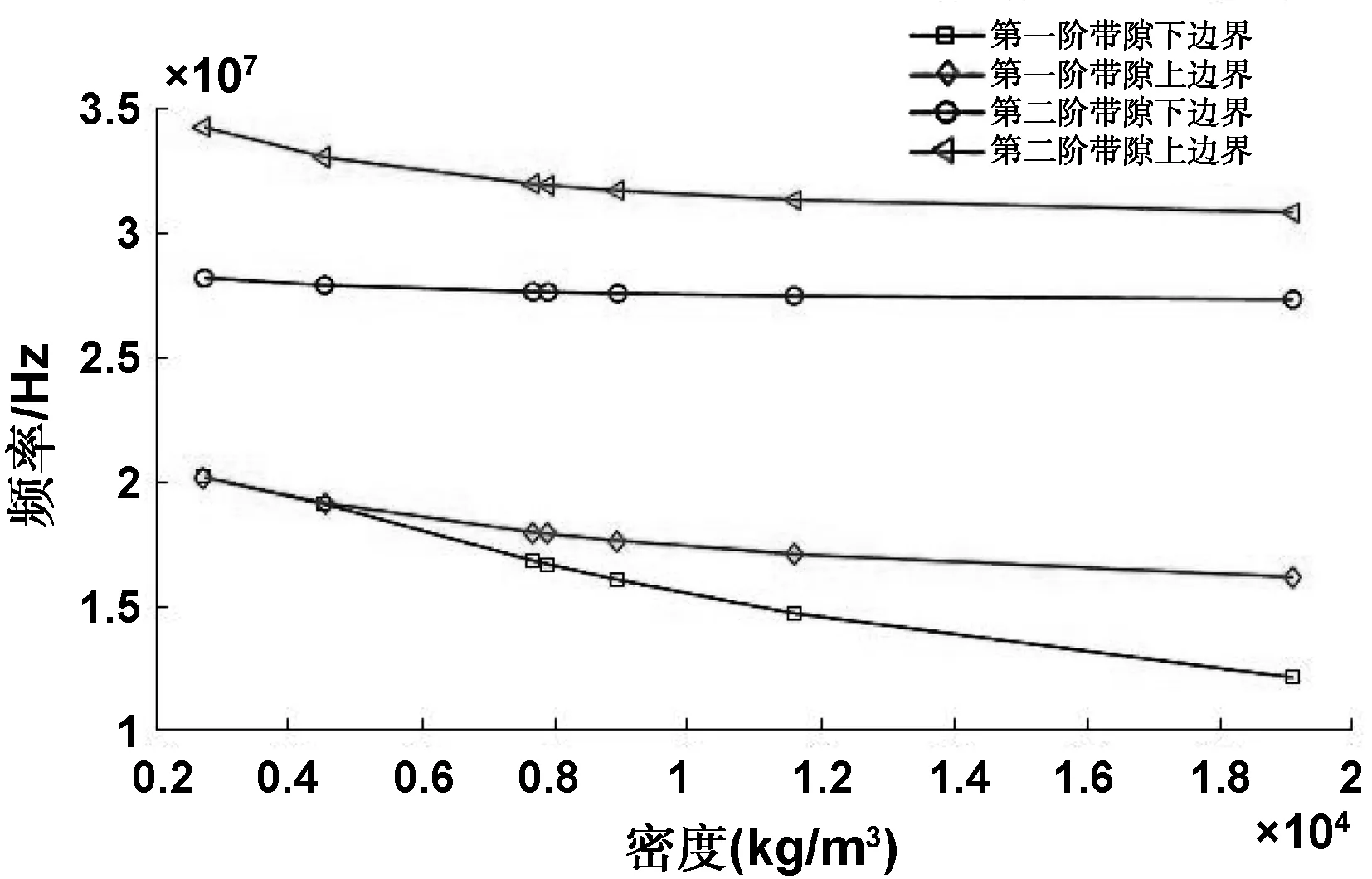
图14 禁带上下边界随芯体密度变化关系图Fig 14 Relationship between the upper and lower boundaries of the band gap and the density of the core

3 结 论

(1)设计了一种基于磁流变弹性体声子晶体的元胞结构，通过调参与计算找出元胞能带结构中存在的受元胞结构和晶格对称性保护的K点必然简并狄拉克点，并通过打破晶格结构空间对称性同时引入质量差的方法使简并点打开并完成拓扑相变过程。

(2)利用拓扑相变的两种类型的元胞结构构造超胞，通过对超胞能带图的计算，在超胞的杂化边界处发现了拓扑边界态，并通过引入了非零谷陈数的观点验证了K点简并打开并产生了谷赝自旋态，超胞在频率freq=2.7483×107Hz和freq=3.0359×107Hz时出现了拓扑边界态，拓扑边界外频率响应被抑制。

(3)通过构造直线型和Z字型拓扑边界并用COMSOL Multiphysics©仿真计算，证明了拓扑边界态可以实现对弹性波的精确引导，按照设计的路线进行高效传播。同时通过对设计的通道引入缺陷并进行仿真计算，证明了拓扑边界对于缺陷的鲁棒性。

(4)通过改变外加磁场强度与拓扑通道传输频率范围的关系，发现随着磁场强度的增加，拓扑通道的传输频率朝高频移动，并且禁带下边界变化速率高于上边界导致禁带宽度减小，当磁场强度达到796 kA/m时，禁带关闭。通过此结论可以实现对拓扑通道传输频率范围实现非接触式智能调控。通过研究元胞芯体材料密度与禁带范围的关系，发现拓扑通道随着芯体密度增加带隙朝低频移动，带隙宽度减小，此结论可以为拓扑通道传输频率范围的被动调控提供参考。