秸塑复合材料的非线性黏弹塑性分析*
2021-06-07张思成盛冬发安文静刘邦剑齐荣庆程家幸
张思成,盛冬发,安文静,刘邦剑,齐荣庆,程家幸
(1. 西南林业大学 土木工程学院,昆明 650224; 2. 东南大学 土木工程学院,南京 210096)
0 引 言
随着人口迅速增长和人类社会的不断进步,工业及生活排入的废弃物不断增多,全球气候和环境问题日益恶化,自然生态平衡受到猛烈的冲击和破坏。从保护生态环境的需要出发,促使人们开始逐步形成以低能量、低消耗、低开支为核心,低碳生活方式已渐渐成为一种时尚。开发和使用环境友好型材料,不仅符合当前社会提倡的低碳环保可持续发展的主题,而且对于国家经济以及材料部门的可持续发展尤为重要。
天然植物纤维具有资源丰富、可再生、可降解、比强度高和质轻价廉等优势,开发环境友好的天然纤维增强树脂基复合材料将会有很大的发展机遇,同时将受到社会各界和各领域的高度关注。由于天然植物纤维的环境友好性,这种纤维增强的复合材料以其独特的环保优势正逐渐成为玻璃纤维增强复合材料的替代品,有着广泛的工程背景和应用前景[1-3]。中国农作物主要以小麦和水稻为主,每年产出秸秆的总量约7亿吨。然而我国对农作物秸秆的利用处理方法还相对落后,除了造纸和作为牲畜饲料外,大多数仍是以掩埋或焚烧方法处理,不仅浪费资源同时还造成了环境污染[4-5]。针对我国的这种现状,秸秆的合理有效化利用就成为了迫切的需求。同时由于全球能源短缺与环境气候问题的恶化等有关环境能源问题的严峻趋势,利用可再生的生物资源以用来制造新型复合材料,就愈发引起了人们的高度重视[6]。秸塑复合材料(SPC)是以废弃秸秆为原材料[7-8],具有生物降解性与可再生性,可应用于高温、长期荷载等工作环境中,在环境保护和节约资源方等面均具有重要的意义,并被世界上许多国家列为新型环保节能绿色产品[9]。秸塑复合材料作为一种新型复合材料,其产品在美国、英国、法国、日本等发达国家的各行业尤其是建筑行业得到广泛应用,而在我国的应用仍有待提高[10]。随着秸塑复合材料的广泛应用,其静动态蠕变特性已成为工程界一项重要课题,引起材料和力学研究人员极大兴趣,美国材料实验协会(ASTM)现已出台了秸塑复合材料的相关标准[11-15]。然而,国内对秸塑复合材料的研究大都侧重在材料制备方法上,而对于其材料蠕变特性的研究相对较少,关于秸塑复合材料的蠕变模型研究仍未见报道[16-18]。
本文利用经典的Schapery非线性黏弹性模型和改进的黏塑性模型,根据拉伸蠕变恢复实验确定模型参数,并利用Schapery非线性黏弹塑性模型预测不同载荷水平下秸塑复合材料的蠕变响应。将理论结果与实验结果进行对比,验证了Schapery非线性黏弹塑性模型的正确性,可用来预测秸塑复合材料在不同应力水平下的蠕变响应。
1 蠕变模型
根据文献[19],在单向载荷作用下,非线性黏弹塑性本构关系可表示为
(1)
式中:第一项表示初始应变,它可能是应力的非线性函数。第二项是相对于缩减时间的积分,缩减时间表示为
(2)
这里aσ是与应力相关的时间尺度因子(也称为移位因子)。如果应力足够小,则有g1=g2=aσ=1。这种情况下,式(1)即为线黏弹塑性应力—应变关系。式(1)最后一项表示整个加载历史过程中累积的黏塑性应变。
对于如图1所示的蠕变试验,应力可表示为σ=σ[H(t)-H(t-t1)],这里H(t)是Heaviside阶跃函数。由方程(1),蠕变应变可写为

图1 蠕变试验中应力和应变Fig 1 Stress and strain in creep
(3)
恢复应变可写为
εr=g2σ[ΔS(ψ)-ΔS(ψ-ψ1)]+εpl(t1,σ)t>t1
(4)
这里
(5)
假设线性黏弹性蠕变柔量的瞬态分量是时间的幂函数,即
ΔS(ψ)=Cψn
(6)
式中C和n为不依赖于应力和时间的常数。将式(6)代入式(3),蠕变应变可表示为
(7)
根据式(4),可得恢复应变
(8)
式中
(9)
根据文献[20],塑性应变可表示为

(10)
式中:常数Cpl、M和m由实验确定。对于如图1所示的加载历史,在整个蠕变时间t1内所累积的黏塑性应变为
(11)
假设蠕变试验的蠕变时间延长到t1+t2,则累积的黏塑性应变可写为
(12)
由于在蠕变加载过程中黏弹性应变不断累积,黏塑性应变不能直接测量。然而,卸载后部分蠕变应变恢复,剩余的不可逆黏塑性应变是可以测量的。可以假设:在相同的应力水平下,进行蠕变时间分别为t1和t2两次蠕变产生的总黏塑性应变,等于蠕变时间为t1+t2产生的黏塑性应变。根据这一假设,蠕变试验在应变恢复期间的中断不影响下一步的黏塑性变形,即
(13)
推广上面的结论,在相同的应力水平作用下,经过k步蠕变所生的总黏塑性应变可表示为
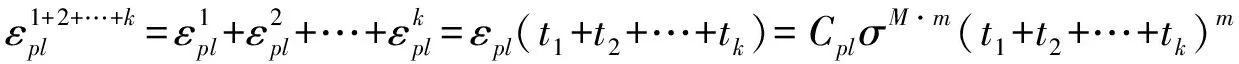
(14)
上述分析表明:在恒定应力σ0作用下,可通过蠕变试验得到试件的黏塑性应变随时间的变化关系。假设材料的黏塑性应变是时间的幂次函数,即
εpl(t)=Btm
(15)
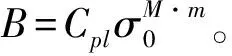

(16)
由式(16),可得
(17)
2 蠕变实验
实验原料选用德州临邑无畏同创农业科技有限公司生产的小麦秸秆粉(60目筛)以及杭州长惠进出口公司生产的HDPE回收废弃塑料。将秸秆粉经干燥处理后,按照与HDPE回收废弃塑料所占配料比约为70∶30进行混合,再加入粘合剂采用热压工艺进行制备,将所制备的秸塑复合材料通过制样机加工后即得到实验所用试件,且试件尺寸为180 mm×10 mm×5 mm。在蠕变试验中为了防止夹头夹断纤维,保障试样断裂尽可能发生在中部,在试样的端部粘结了加强片,加强片选用尺寸为30 mm×10 mm×3 mm的铝板制作,胶接加强片所用的胶粘剂为环氧树脂,两侧加强片在粘结中应对称,形成哑铃形状,如图2所示。

图2 复合材料试样形状示意图Fig 2 Schematic diagram of composite sample
拉伸实验按照GB1447—2005测试,拉伸速率为20 mm/min,在长春实验机研究所生产的CSS44020型电子拉伸实验机上进行。首先,试样在15 MPa单向拉伸应力作用下进行时长分别为1、4、21和48 h的蠕变试验,以得到在恒定应力水平下的黏塑性应变随时间的关系,如图3(a)所示。从图可以看出,蠕变在刚开始的1 h内黏塑性应变快速发展,此后黏塑性应变的发展随着时间的增加而逐步减缓。
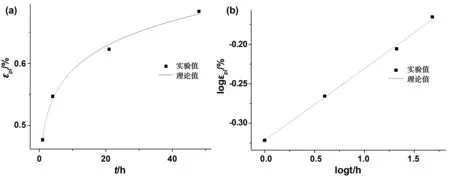
图3 15 MPa单向拉伸应力作用下黏塑性应变随时间变化规律Fig 3 Variation of viscoplastic strain with time under 15 MPa uniaxial tensile stress
3 模型参数确定与分析
3.1 确定Schapery模型参数


(18)
这样,计算Cpl,可得
引入变量
(19)
这样,对式(8)同取对数可写为
log(εr-εpl)-logX=log[(1+y)n-yn]
(20)
式(20)表明,若以y作为时间变量,并在垂直坐标上平移logX,则各应力水平的应变恢复曲线必定重合。这个特性为确定两个未知变量X和aσ提供了一种简化方法。则可将函数
Z=log[(1+y)n-yn]
(21)
定义为主曲线。下面我们可以利用实验曲线,把X和aσ作为拟合参数来拟合此曲线。考虑材料在线性响应区域的应变恢复系数,假设试件在8 MPa单向应力作用下满足线黏弹塑性应力-应变关系,此时g1=g2=aσ=1,因此有
(22)
图4为在应力σ0=8 MPa水平条件下,蠕变8 h后进行恢复得到的黏弹性应变和恢复时间的实验数据,相应的应力水平下黏弹性应变主曲线。

图4 8 MPa应力作用下的恢复黏弹性应变主曲线Fig 4 Recovery viscoelastic strain master curve under 8 MPa
从图4中得到式(6)中幂函数指数n的数值,并根据主曲线的定义和性质,得到应力σ0=8 MPa水平条件下的黏弹性拟合参数X和aσ。通过实验数据和曲线拟合分析,可得到幂指数n=0.1506。当σ0=8 MPa时,X=0.2574%,aσ=1,其他应力(σ0=12、16、20 MPa)水平下的拟合参数X、aσ见表1。

表1 黏弹性的拟合参数
在拉伸恢复蠕变实验中,所记录的蠕变应变为黏弹性应变和黏塑性应变的总和,蠕变后的黏塑性应变是恢复曲线的最终应变值。用它们从测量应变中减去黏塑性应变,得到纯非线性黏弹性应变。在蠕变试验中黏塑性应变随时间的关系可表示为
(23)
这里
(24)
tk是蠕变周期的长度。式(23)的优点是黏塑性应变直接来源于实验结果,并不需要明确黏塑性应变的应力依赖关系。根据式(7),非线性黏弹性应变可表示为
(25)
上式也可以写为
εc-ε0-εpl(t,σ)=C′tn
(26)


图5 8 MPa应力作用下的非线性黏弹性柔量与时间关系Fig 5 Relationship between nonlinear viscoelastic compliance and time under 8 MPa

(27)


表2 非线性黏弹性材料的特征参数
值得一提的是,弹性应变ε0并不是真实的弹性响应。为了更好地描述蠕变试验中的应变,采用幂律表达式(7),而ε0只是这个表达式中的常数项。当应力达到20 MPa时,n可能不再仍然保持为0.1506。此时对表2中的数据用简单的分析函数来近似,即
(28)
(29)
(30)
(31)
3.2 模型预测结果与试验结果验证
为了验证Schapery非线性黏弹塑性模型对秸塑复合材料蠕变性能预测的准确性,将表2中所拟合得到的各个参数代入式(1)中,即可得到不同应力作用下秸塑复合材料的蠕变应变随时间的变化规律。将模型预测结果与实验结果进行对比,对比结果如图6所示。从图6中很容易看出,本文的Schapery非线性黏弹塑性模型所预测的结果与实验结果基本一致,其预测结果的相关精度可达0.998566,证明Schapery非线性黏弹塑性模型可用于预测秸塑复合材料的蠕变变形。
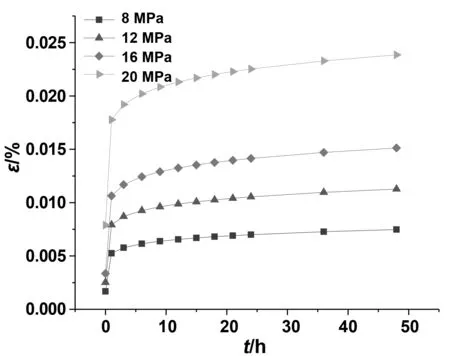
图6 不同应力作用下秸塑复合材料的蠕变响应Fig 6 Creepresponse of straw plastic composite under different stress
4 结 论
(1)对秸塑复合材料进行不同应力条件下的拉伸蠕变实验,分别得到了15 MPa应力条件下黏塑性应变随时间的变化规律,8 MPa应力条件下蠕变8 h后进行恢复的黏弹性应变与时间的关系,8 MPa应力条件下非线性黏弹性柔量和时间的关系,以及不同应力条件下秸塑复合材料蠕变应变随时间的变化规律。
(2)通过最小二乘法拟合得到了秸塑复合材料的Schapery非线性黏弹塑性模型本构方程中的各个参数,从而得到了Schapery非线性黏弹塑性模型的理论模型。并将该模型的预测结果与实验结果进行对比,结果表明该理论模型可对秸塑复合材料在不同应力条件下的蠕变行为进行较好的预测,其预测相关精度可达0.998566。通过以上分析,说明本文采用的Schapery非线性黏弹塑性模型可较好地描述秸塑复合材料的黏弹性力学行为。
