滚轮曲线的等时性证明及其在物理问题中的应用
2021-06-07陈建文
王 磊 陈建文
(1.盘锦市高级中学,辽宁 盘锦 124010 2.盘锦市辽东湾实验高级中学,辽宁 盘锦 124010)
1 滚轮曲线
单摆模型是高中物理经典的物理模型之一,当单摆的摆角很小时,我们认为单摆的摆动周期是一个定值,这个周期与摆角无关只与摆长有关.对单摆研究最深入的科学家是惠更斯,但最初发现单摆摆角很小摆动周期不变的科学家是伽利略,伽利略是一位伟大的科学家的同时也是一位虔诚的天主教徒,有一次伽利略在教堂礼拜时,发现教堂穹顶的吊灯在摆动,善于发现问题的伽利略敏锐地觉察到,虽然摆动的幅度在改变,但来回摆动的时间却是相同的,于是伽利略一边摸着自己的脉搏一边观察这吊灯的摆动,果然验证了自己的想法,后来惠更斯还根据单摆的等时性发明了单摆时钟.但是单摆的周期是与摆角严格的没有关系么.显然不是,在中学物理课上,教师推导单摆周期公式需要用到sinθ≈tanθ≈θ在角度很小时的近似相等,可见单摆的周期在角度变化时是有微小的差别的.那么有没有一种摆动的周期是严格相等,与摆角或振幅无关的呢?
惠更斯在研究单摆问题时也思考了同样的问题,并且他得到了答案,答案的灵感来源于数学上的一种有名的曲线——滚轮曲线.我们先看何为滚轮曲线?轮子在水平面上做无摩擦的滚动,轮子边缘一点的运动轨迹即为滚轮曲线.滚轮曲线既不是圆也不是椭圆,而是独立于圆锥曲线之外的一种新型曲线.
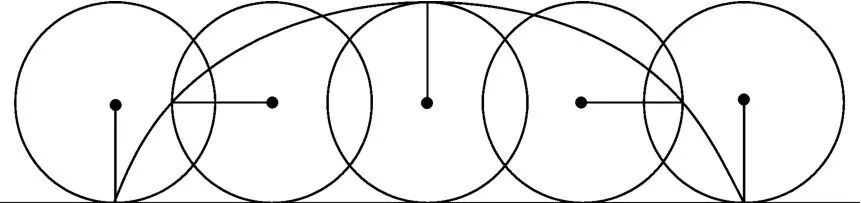
图1
以轮子边缘一点在最低点处为原点,建立直角坐标系,该点的轨迹方程为x=Rθ-R sinθ;y=R-R cosθ.该轨迹与轮子的转动快慢并无关系.轨迹方程只由轮子半径决定.[1]

图2
2 滚轮曲线的等时性证明
以竖直向下为正方向,半径为R的轮沿x轴滚动,以其边缘某一点的运动轨迹曲线为一小球的滚动轨道.轨道光滑,设小球的出发点为轨道上任意一点A,A点对应滚轮转过的角度为θ0,[2]滚轮滚动到x轴的P点.经过时间t小球滑动到该滚轮线的B点,B点对应滚轮转过的角度为θ,滚轮沿x轴滚动到Q点.从滚轮线角度研究小球在B点的线速度v有该速度v与滚轮线相切.把小球在B点的运动视为滚轮沿x轴滚动到Q点时B点处滚轮边缘的运动.可知该运动可视为Q位置时滚轮圆心C的速度v0与B点处滚轮边缘相对于圆心的速度的合成.由于C绕Q瞬间角速度与B处轮缘绕C瞬间角速度相同,故B点处滚轮边缘相对于圆心的速度大小也是v0.设v与圆心C速度v0的夹角为α,根据几何知识可得2α=π-θ,且有重力作用下小球沿滚轮曲线运动的切向加速度aτ=g sinα,故有

图3

由(6)式可以看出,在光滑滚轮曲线上来回滑动小球的运动周期只与滚轮曲线的滚轮半径有关,与初始位置无关,故滚轮曲线又称为等时曲线或等时摆线.
3 滚轮曲线在物理问题中的应用
例1.在不同的高度上有O、D两点,O、D两点连线长为l,与水平方向夹角为φ,在O、D两点间建立一条光滑轨道使小球从O在重力作用下沿轨道自由滑下,求能使小球滑到D点的最短时间和相应的轨道形状.
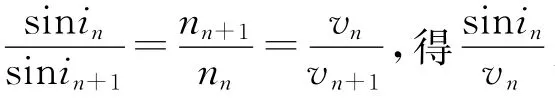

图4
而以O点为坐标原点,竖直向下为y轴建立坐标系下的某一半径为R,起点为O的滚轮曲线即能满足上述轨道条件.
根据(3)式,从O点释放的小球滑到对应滚轮转过圆心角为θ处的速度为
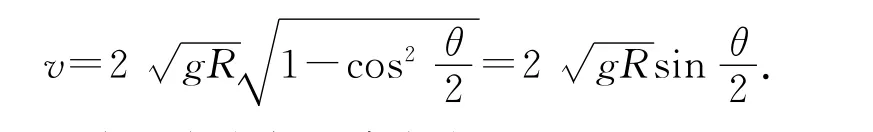
速度v方向与竖直方向夹角i,结合图3,图5可得,故有为定值,故对比光学费马原理可知该半径R的滚轮曲线即为O、D两点间用时最短的轨道.从O点释放小球,(6)式θ0=0变为
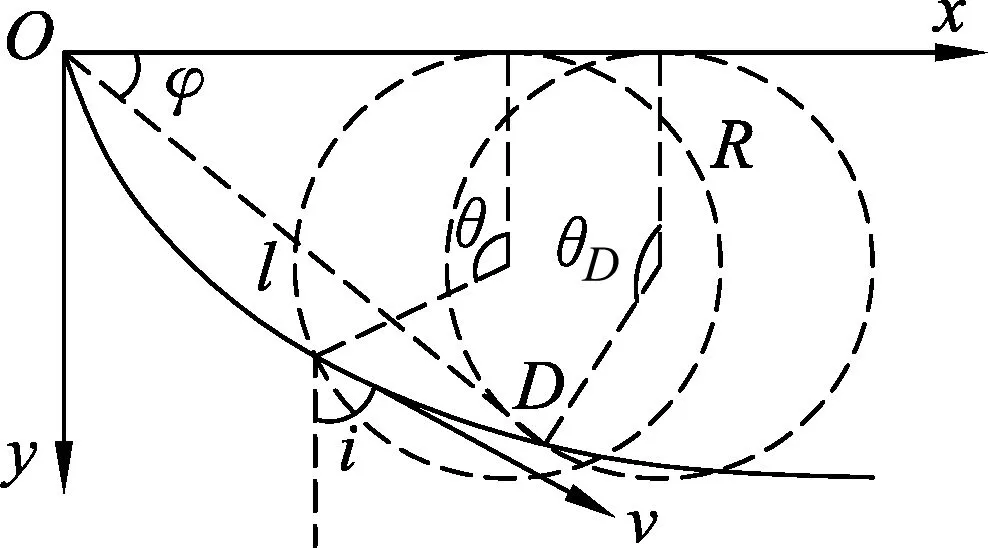
图5
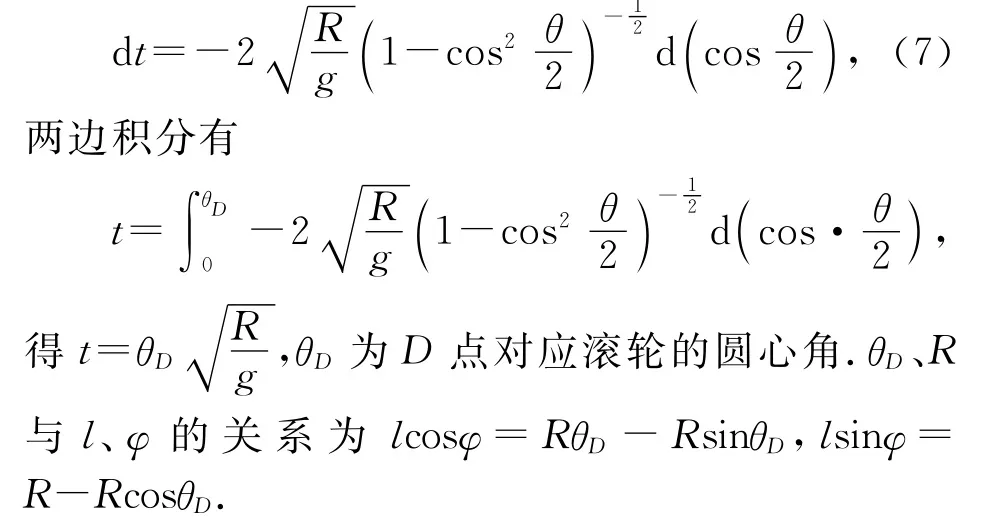
例2.一带电量为+q的粒子处在竖直向下电场强度为E的匀强电场和垂直纸面向里的磁感应强度为B的匀强磁场中,静止释放该电荷,求电荷的运动轨迹.

图6

