基于灰色线性回归组合模型的中国高职教育规模影响因素及预测研究
2021-06-07李志勤
李志勤
(四川商务职业学院 经济贸易系,四川 成都 610000)
据2018年全国教育事业发展统计公报显示中国建国七十年以来,高等教育毛入学率从1949年的0.26%提高到2018年的48.1% ,高等教育大众化水平进一步提高,提前实现了国务院《国家中长期教育改革和发展规划纲要(2010-2020年)》中中国高等教育毛入学率达到40%目标。截至2018年底,全国高校2663所,其中高职院校1418所,占高校总院校数量53.25%,全国高校在校学生总规模达3833万人,其中高职院校在校学生人数占全国高校在校学生总人数的40.05%。改革开放四十年以来,伴随中国经济的发展,中国高等教育质量取得了历史性的成就和发展,为中国从高等大学到高等教育强国转变发挥着重要的作用。
一、研究现状综述
在中国高职教育规模研究中,学者们研究领域集中于高职教育与经济发展相关性研究及基于区域性高职教育规模研究方面,[1]目前,对全国范围内高职教育规模预测研究尚数空白领域。
在学术研究中的高职教育规模研究方面,孔颖(2006)研究“十一五”期间我国高职教育规模发展途径及应注意的问题;[2]高振强(2007)基于宁波高职教育发展现状、发展动因研究宁波高职教育规模;[3]张佳(2015)建立对数线性模型预测四川省2014-2023年高职教育在校生人数;[4]花鸥(2017)基于经济发展和人口因素通过SPSS线性相关性模型预测“十三五”江苏高职教育发展规模及预测。[5]
在高职教育与经济发展相关性研究方面,李中国(2016)提出西部高职院校规模与布局直接影响到西部经济的协调和可持续性发展;[6]李志刚(2013)提出经济增长对高职教育有正向的推动作用;[7]高娟(2017)通过对OECD国家高职教育宏观投入数据计量回归分析,得出伴随经济增长,各国高职总投入未呈现明显的规律性,经济发展需求导致了高职教育萎缩与消失;[8]王伟(2017)提出职业教育规模和质量对我国经济有利。[9]
二、灰色模型构建
(一)数据分析
基于原始数据的真实性、可获得性、可追溯性和可比性原则,本文以2005年至2016年中国国家统计局《中国统计年鉴》及中国教育部《中国教育经费统计年鉴》进行数据统计及整理分析。中国高等教育范围包括普通高等学校、高职高专学校及成人高等学校,本文研究范围仅包括高职高专学校不包括普通高等学校及成人高等学校。
(二)灰色相关性分析
1.影响中国高职教育规模发展因素
影响中国高职教育规模发展因素很多,在通过文献整理和研究现状的基础上,[10-14]本文选用4个一级指标,8个二级指标,总共8个影响因素分析高职教育影响因素。见表1。

表1 高职教育规模影响因素
为减少因为数据单位对计算分析精确性和正确性的影响,对原始数据进行无量纲化处理,即每个原始数据除以平均值,无量纲化处理后数据如表2。

表2 无量纲化处理后高职教育规模及影响因素数据
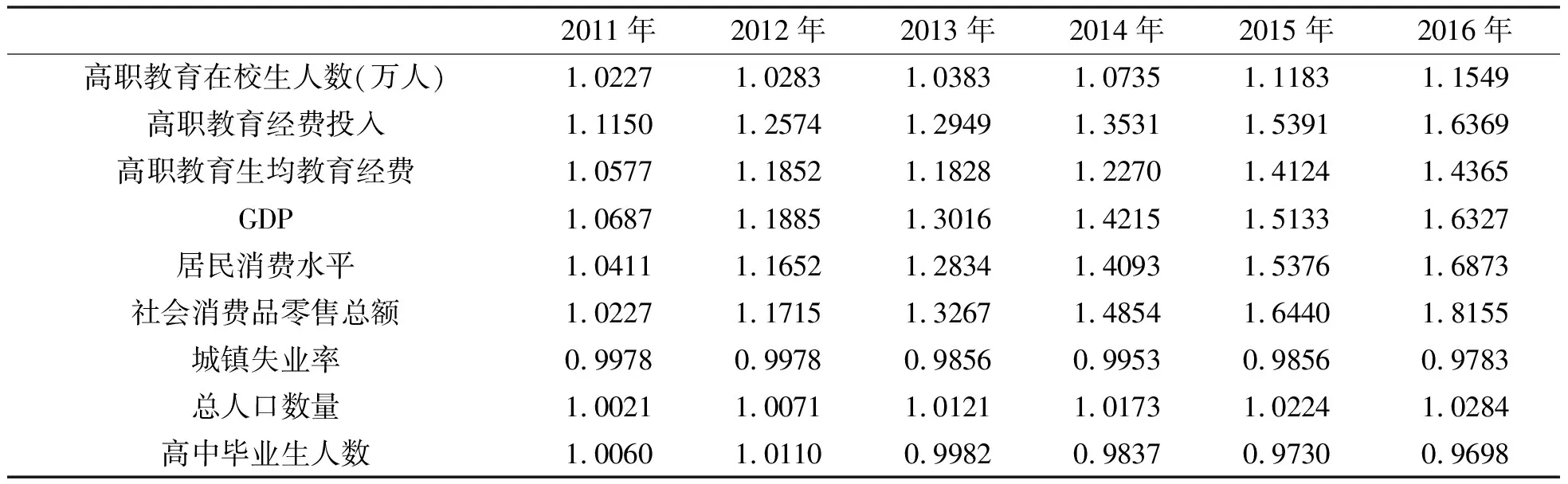
2011年2012年2013年2014年2015年2016年高职教育在校生人数(万人)1.02271.02831.03831.07351.11831.1549高职教育经费投入1.11501.25741.29491.35311.53911.6369高职教育生均教育经费1.05771.18521.18281.22701.41241.4365GDP1.06871.18851.30161.42151.51331.6327居民消费水平1.04111.16521.28341.40931.53761.6873社会消费品零售总额1.02271.17151.32671.48541.64401.8155城镇失业率0.99780.99780.98560.99530.98560.9783总人口数量1.00211.00711.01211.01731.02241.0284高中毕业生人数1.00601.01100.99820.98370.97300.9698
2.影响高职教育规模因素灰色相关性分析

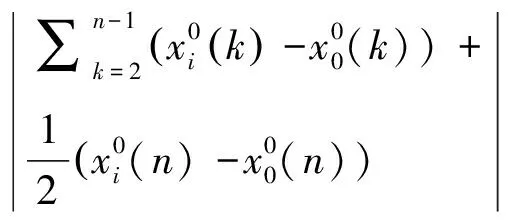
灰色绝对关联度公式:
通过灰色相关性分析,得出高职教育在校生人数与8个二级指标的相关性见表3。

表3 高职教育在校生人数与影响因素之间灰色相关性分析表
从计算结果来看,各影响因素与高职教育在校生人数相关性系数均大于0.6。其中高职教育在校生人数与城镇失业率、总人口数量、高中毕业生人数的灰色关联度约为0.6,且小于0.7,即城镇失业率、总人口数量、高中毕业生人数对高职教育在校生人数影响并不大,在线性回归中,可以剔除上述三个影响因素。在社会经济发展水平衡量指标中社会消费品零售总额与高职教育在校生人数相关性最低,可以剔除。综述所述,最后用于线性回归测试的指标包括高职教育经费投入、高职教育生均教育经费、GDP、居民消费水平共4个指标。
(三)灰色模型分析
1.灰色模型理论
中国学者邓聚龙于上世纪80年代创立了灰色系统理论,该理论是研究少数据、贫信息不确定性问题的新方法。[15]中国高职教育规模因为受影响因素共同作用,与诸多因素有密切关联,且各种变量对高职教育规模的具体影响作用程度、影响频率、运行机理等具有不确定性,因此适合灰色系统理论研究范畴,所以将整个中国高职教育规模作为一个具体灰色系统进行分析是适合的。[16-17]
设X(1)为原始序列X0的1—AGO序列,Z(1)为X(1)的紧邻均值生成序列
(1)准光滑性检验,即序列X中的数据变化越平稳,其光滑比∂(k)越小,满足条件则可建G(1,1)。
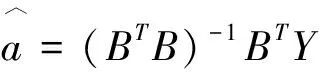
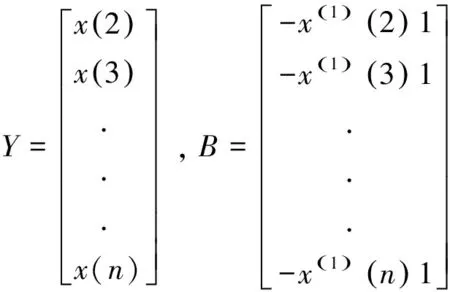
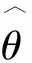
(4)Verhulst模型为:x(k)+aZ(1)(k)=b(Z(1)(k))2
2.灰色模型实证分析
2011年与2010年相比高职教育在校生人数增长率为-0.76%,为提高预测的准确度,本文采用增速变化为正值的2011年-2016年这一最近时期我国高职教育在校学生人数对我国未来高职教育在校学生人数进行GM(1,1)模型预测并检验。
X为给定的序列,则x=(x(1),x(2),x(3),x(4),x(5),x(6))=(1.0227, 1.0283, 1.0383, 1.0735, 1.1183, 1.1549)
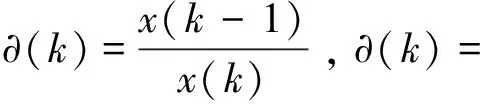
(0.9945,0.9711,0.9672,0.9599,0.9683),可容覆盖为n=6,∂(0)(k)∈(0.7514,1.3307),∂(k)均落于可容覆盖,表明该序列可作GM(1,1)建模和进行数列灰预测。
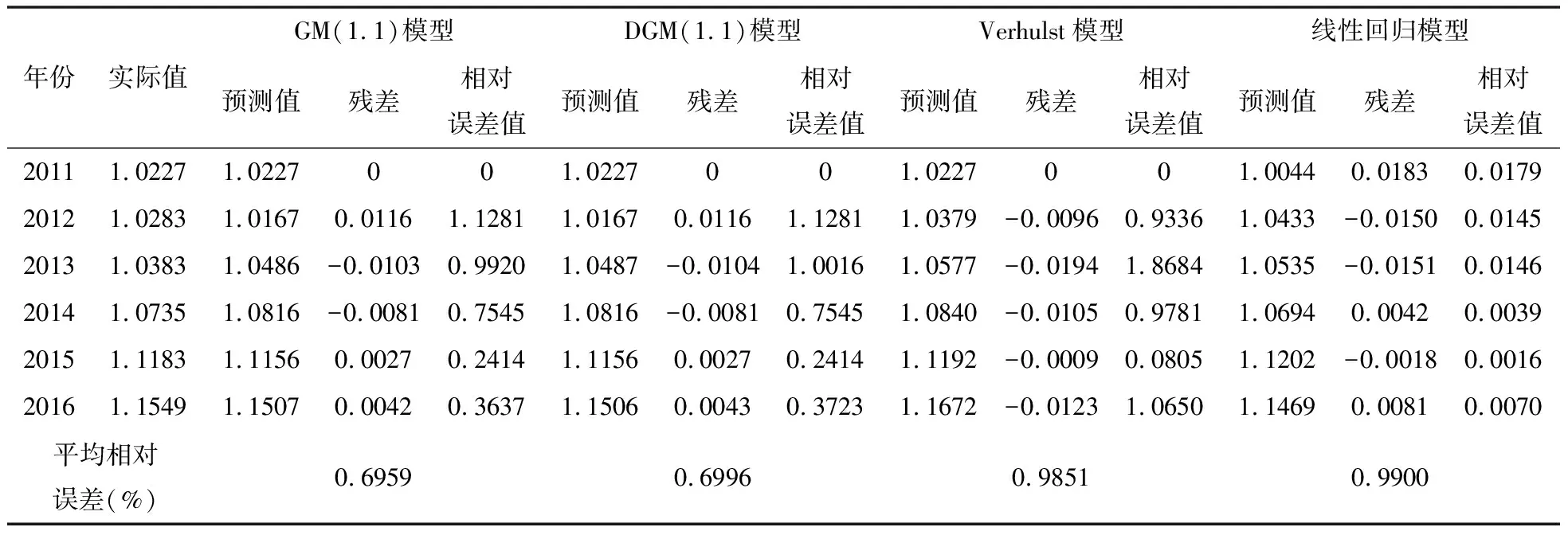
表4 GM(1.1)模型、DGM(1.1)模型、Verhulst模型、线性回归模型预测值及相对误差分析
3.灰色预测模型精度分析
在平均相对误差检验中,GM(1,1)模型、DGM(1.1)模型、Verhulst模型平均相对误差分别为0.6959 %、0.6996%、0.9851%,均小于0.01为精度一级。
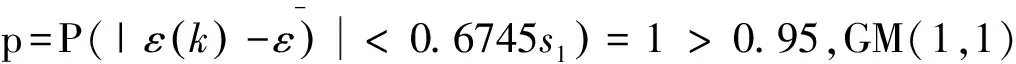
相关性检验中,GM(1,1)模型、DGM(1.1)模型、Verhulst模型实际值与预测值灰色关联绝对相关性分别为0.9645、0.9644、0.8529,除Verhulst模型外,GM(1,1)模型和DGM(1.1)模型的实际值与预测值灰色关联度大于0.9,为精度一级。
综上所述,GM(1,1)模型在平均相对误差检验、后验差检验、小误差概率检验及灰色关联性检验均优于DGM(1.1)模型、Verhulst模型,因此在建立组合模型中,采用GM(1,1)模型精度更高。
三、线性回归模型构建
(一)线性回归模型
在线性回归中,y为高职教育在校生人数、a为高职教育经费投入、b为高职教育生均教育经费、c为GDP 、d为居民消费水平。运用SPSS25分析软件,进行线性回归,采用步入法代入数据。结果分析如下:
1.模型拟合情况
如图1所示,修正的可决系数(调整后的R方)为0.925,模型的解释能力非常好。

模型摘要模型RR方调整后 R 方标准估算的错误1.969a.940.925.0147881a.预测变量:(常量), a
2.方差分析
如图2所示,模型的检验P值(Sig)为0.001,小于0.05,模型整体很显著。
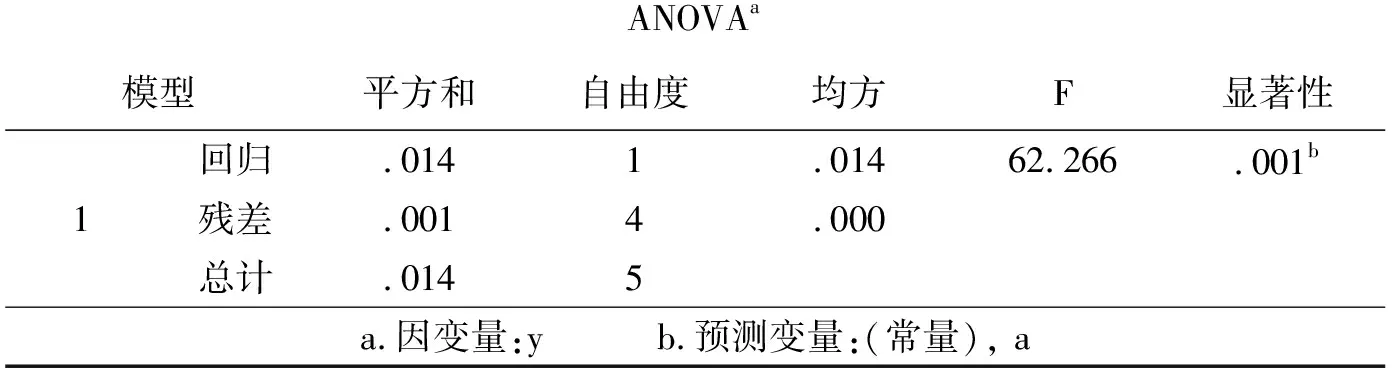
ANOVAa模型平方和自由度均方F显著性1回归.0141.01462.266.001b残差.0014.000总计.0145a.因变量:y b.预测变量:(常量), a
3.回归方程的系数及系数的检验结果
如图3、图4所示,变量b、c、d的显著性均大于0.05,所以剔除。模型的表达式为:高职教育在校生人数=0.7+0.273*高职教育经费投入(即y=0.7+0.273*a)
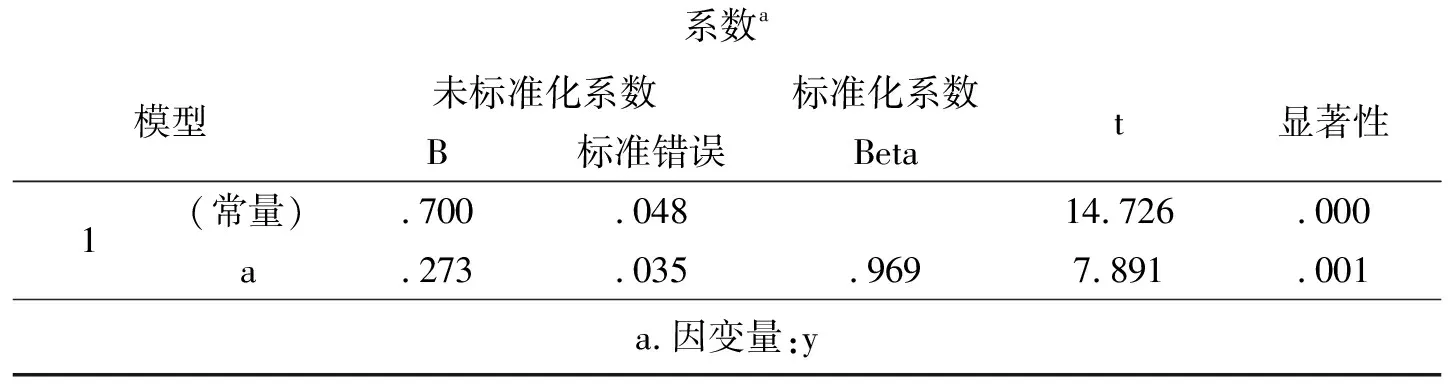
系数a模型未标准化系数标准化系数B标准错误Betat显著性1(常量).700.04814.726.000a.273.035.9697.891.001a.因变量:y
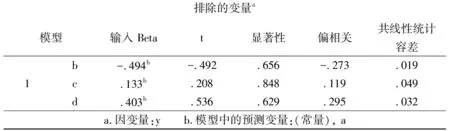
排除的变量a模型输入 Betat显著性偏相关共线性统计容差1b-.494b-.492.656-.273.019c.133b.208.848.119.049d.403b.536.629.295.032a.因变量:y b.模型中的预测变量:(常量), a
(二)线性回归模型精度分析
线性回归模型平均相对误差为0.99%,符合建模精度要求,见表3。
四、灰色线性回归组合模型
灰色线性回归组合模型分别对灰色预测模型和线性回归模型进行了优化和改善。建立灰色线性回归组合预测模型的一个重要步骤是对组合权重进行优化, 其目的是通过选择组合权重向量, 使线性组合预测模型的精度满足预测对象的要求。
(一)构建组合模型
设 GM ( 1,1 ) 模 型 为f1(x),多元回归模型为f2(x),ω1、ω2为权重,灰色线性回归组合模型为f(x)
f(x)=ω1f1(x)+ω2f2(x)
计算权重方法很多,如熵值法、算术平均法、层次分析法、最优加权法等。本文选取Shapley 值法确定权重,该法是1953 年Shapley 教授提出的用于解决多人合作对策的数学方法,可实现团队总收益在各成员间的公平有效分配。
(二)Shapley 值法[18]
-E(s-{i})]
Ei为shapley值,s为包括交易i的组合,i为组合中某个预测模型,|s|为组合中预测模型的个数,n为参与组合预测的预测模型总个数,s-{i}为组合中去除成员i
(三)模型权重计算
各成员的Shapley :
将ω1、ω1代入组合模型为:
f(x)=0.6745f1(x)+0.3255f2(x)
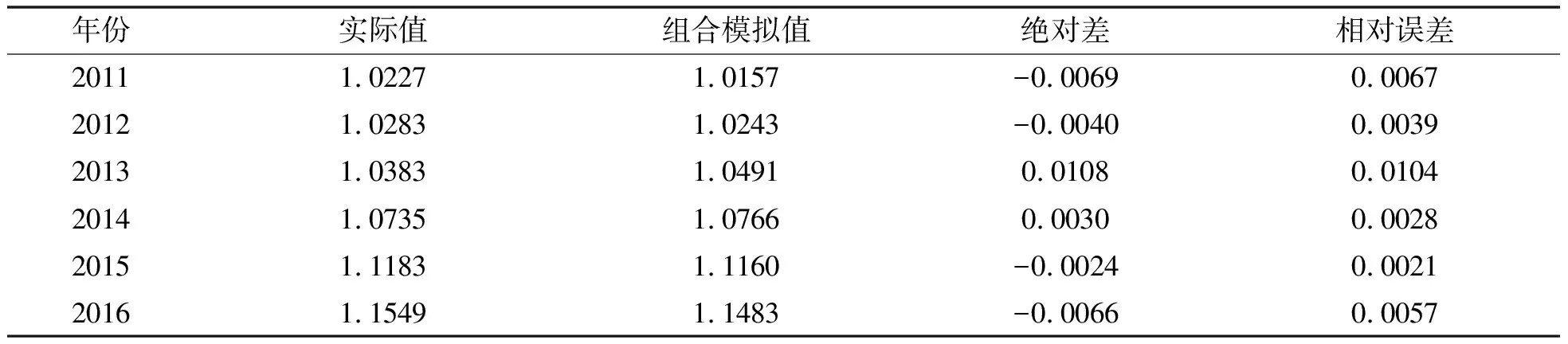
表5 灰色线性回归组合模型预测值及相对误差分析
(四)灰色线性回归组合模型精度及预测
灰色线性回归组合模型平均相对误差为0.5282%,小于GM(1,1)及线性回归模型平均相对误差,组合模型降低了预测模型误差率,所以在预测中选择组合模型更能让预测更精准。
通过灰色线性回归组合模型预测2017年至2021年高职教育在校生人数,见表6。

表6 2017年至2021年高职教育在校生人数预测值
经灰色线性回归组合模型预测2017年,2018年,2019年,2020年,2021年高职教育在校生人数分别为111.00万人、114.45万人、118.05万人、121.82万人和125.77万人。
五、结论
(一)通过预测中国高职教育规模,预计未来一定时期内,中国高职教育将保持现有规模并保持稳定低速增长的趋势。
(二)通过灰色线性回归模型的构建,降低了原有灰色模型及线性回归模型误差率,提高了建模精度,并且优化改善了灰色模型没有考虑线性变化趋势及线性模型没有涉及指数增长的缺陷,经实证分析,构建的灰色线性回归模型精度高,能够很好预测高职教育在校生规模,通过灰色线性回归模型预测在2020年高职教育在校生人数将达到120万人以上。
(三)在影响高职规模诸多因素中,影响因素众多,各种因素作用机理及重要性尚不明确。高职教育投入因素与高职教育规模的灰色关联度高,表明高职教育投入是高职教育规模发展的决定性因素,但城镇失业率、总人口数量、高中毕业生人数却对对高职教育规模发展影响较少。经济发展水平因素GDP、居民消费水平、社会消费品零售总额对高职教育规模无显著性影响。
(四)研究表明高职教育经费投入与高职教育在校生规模有明显的线性关系,说明了高职教育的发展仍然依赖于教育的投入。国家在布局高等教育中,不但要考虑高等教育顶层设计,要建设高职教育体系建设,构筑质量保障机制,而且要完善教育经费来源。未来很长一段时期内,国家加大对高职教育投入,更能加速中国高职教育的发展。[19]
(五)伴随着经济的增长,全国高职教育的规模同步增长,经济发展与高职教育呈现出同向提升和发展的现状和趋势,这从总体上说明了经济增长对高职规模教育有正向的引导和推动作用。经济的发展与高职教育关系表现在高职教育为经济增长提供满足其自身发展刚性需求必须的教育规模的需要。[20]
