结合自适应亮度变换不等式估计透射率的图像去雾方法

杨燕,陆鑫璇

(兰州交通大学电子与信息工程学院,730070,兰州)

在雾霾环境下,受到大气中的悬浮颗粒和水滴对光线进行散射的影响,户外成像设备捕获的图像会出现严重退化,表现为清晰度低、对比度低、信息量少等问题,对人们的日常生活造成极大的影响。因此,对有雾图像进行去雾获得清晰的无雾图像具有十分重要的研究意义[1-2]。

图像去雾方法主要分为3大类。第1类是基于图像增强的去雾方法[3-5],该方法基于非物理模型,仅从提高对比度、强化细节方面达到对图像进行增强去雾处理,但没有充分考虑雾天图像降质的因素,增强处理后效果不自然,主要有直方图均衡、小波变换和Retinex算法[3]等。第2类是基于图像复原的去雾方法[6-10],通过参考雾天成像物理模型,加以一定的先验条件或者图像信息,从图像复原角度进行处理。该类方法能够在复杂场景下获得较好的去雾效果,成为近年来研究的热点和突破的难点。其中,He等提出的基于暗通道先验理论的去雾方法[6],通过大气散射模型复原出无雾图像,虽然该方法取得了显著的去雾效果,但是在恢复包含大片天空区域的图像中会出现天空失真现象,并且采用软抠图优化透射率,存在着算法复杂度高、处理速度慢等问题。此后,He等为了提高处理速度提出引导滤波优化透射率方法[7],但在景深变化剧烈区域有明显的残雾现象。Meng等提出基于边界约束的去雾方法[8],将透射率固有的约束和相邻像素的约束关系相结合,从而增加物理模型的约束条件逼近透射率,通过建立优化透射率的模型实现图像去雾,但该方法牺牲了部分细节特征来提高恢复效果。Zhu等提出基于颜色衰减先验的去雾方法[9],通过HSV空间的V分量和S分量的差值,使用监督学习方法来估计场景深度信息,该方法恢复了较多的细节,但是存在一定的残雾现象,同时学习过程较复杂。Wang等提出基于线性传输的去雾方法[10],通过有雾图像与无雾图像最小通道的正相关性构造线性关系,该方法去雾较彻底,但恢复的图像较暗,颜色失真严重。第3类是机器学习的去雾方法[11-12],该方法通过训练样本来获取模型参数,实现图像去雾。主要有Ren等提出多尺度卷积神经网络的去雾算法[11],采用粗尺度网络对图像预测透射率,以及精细尺度网络进行局部性的优化,其运行速度快。Cai等提出端到端系统的去雾算法[12],通过学习有雾图像与其对应的透射率之间的映射关系。由于训练过程中,采用合成数据集,并且训练的过程需要大量的数据集,因此不适用于多种类型的图像。

针对以上研究的不足,本文基于图像复原的方法,提出一种结合自适应亮度变换不等式估计透射率的图像去雾方法。通过对颜色衰减先验进行亮度变换不等式操作,获取场景深度表达式;并将恒定的大气散射系数向动态的形式转换,使其能够适应不同图像的场景需求;再结合中值滤波和区间估值估计的局部大气光恢复出无雾图像。实验结果表明,本文的方法能够获得较好的去雾效果,同时能实现实时处理。

1 图像去雾背景

1.1 大气散射模型

目前在计算机视觉和图形学领域中,广泛应用于雾天条件下的大气散射模型[13]其数学表达式为

I(x)=J(x)t(x)+A(1-t(x))

(1)

t(x)=exp(-βd(x))

(2)

式中:I(x)表示待处理的有雾图像;J(x)表示恢复出的无雾图像;A表示为无穷远处大气光值;t(x)表示透射率;d(x)表示场景深度;β表示大气散射系数,在假设大气均匀分布的条件下,β通常设为1。

1.2 颜色衰减先验算法

文献[9]对大量有雾图像进行统计分析后提出,对于大多数户外有雾图像而言,任意区域雾的浓度随景深的变化而变化,雾浓度越高,该区域像素点的亮度和饱和度相差越大,即雾浓度与亮度和饱和度之差呈正相关。由于雾的浓度随着场景深度的变大而变浓,因此,可以获得如下关系式

d(x)∝c(x)∝v(x)-s(x)

(3)

式中:c(x)表示雾的浓度;v(x)表示亮度分量;s(x)表示饱和度分量。为了准确表述上式关系,根据正相关表达式,建立线性模型

d(x)=θ0+θ1v(x)+θ2s(x)+ε(x)

(4)

式中:θ0、θ1、θ2均表示未知参数;ε(x)表示期望为0、方差为σ的高斯函数随机误差。通过训练数据集得到θ0=0.121 779,θ1=0.959 710,θ2=-0.780 245,σ=0.041 337。由于表达式倾向于白色物体作为远景处的对象,导致近景区域存在白色物体时会误判为高景深区域,因此假设场景深度是局部恒定的,利用窗口大小为15×15像素的引导滤波[7]平滑场景深度,获得最终透射率。假设大气光已知的情况下,可以恢复出无雾图像,但恢复后的图像存在光晕效应。

同时,文献[9]算法将关键的参数β取为1具有一定的局限性。因为大气并不全是均匀分布,其值可能存在比场景真实值偏大或偏小的问题:当β偏大时,所估计的透射率偏小,使得恢复的图像出现颜色过饱和现象,去雾过度;反之亦然。

2 本文算法

本文提出一种结合自适应亮度变换不等式估计透射率的图像去雾方法,其流程如图1所示。

图1 本文方法流程图Fig.1 Algorithm flow chart

首先,根据雾的浓度与亮度分量和反饱和度分量之间的统计关系,利用亮度变换不等式和对数变换构造粗略的场景深度;其次,基于局部恒定采用正则化对粗略的场景深度进行优化,获得精确的场景深度;然后,利用局部平均深度信息和联合双边滤波得到动态大气散射系数,根据精确的场景深度和动态大气散射系数获得最终透射率;最后,使用中值滤波和区间估值优化局部大气光值,结合大气散射模型恢复无雾图像。

2.1 自适应透射率

2.1.1 场景深度估计 由于式(4)的线性模型具有局限性,参数繁多,且监督学习获取模型数值具有复杂性,需要大量数据集。为了简化模型,将颜色衰减先验变换为雾浓度与亮度分量和反饱和度均呈正相关。因此,对式(3)进行拆分变换,如式(5)所示

(5)

式(5)对于归一化图像设定h≥1时成立。通过实验统计分析,得到雾浓度与亮度和反饱和度之间的关系,图2为雾浓度与场景深度关系。同一幅雾图中的亮度和与反饱和度分布相似,将两个正相关进行乘积,雾浓度与乘积形式亦满足正相关

d(x)∝c(x)∝v(x)(h-s(x))

(6)

为了利用亮度和反饱和度求取场景深度相对最优值,采用式(7)的均值不等式形式构造,现设不等式最右项的系数为u,进行实验对比分析

(7)

u的取值范围为[0.5,1],u取值不同场景深度有较大差异。图3为u取不同值时场景深度比较。由图3可见,当u越小,场景深度图像整体像素值越小,反之亦然。

在大多数雾天图像中,景物距离观察者通常都较远,图像中属于远景区域的像素点应具有较大的深度值,反之亦然。雾图的亮度信息能充分反应雾的分布,且均值不等式在求取最值具有较好表现。结合均值不等式和亮度分量对式(6)进行自适应亮度变换补偿优化,如式(8)所示

(a)有雾图像 (b)对应区域的雾浓度、亮度和反饱和度 (c)雾浓度分析曲线图2 雾浓度与场景深度关系Fig.2 Analysis of the relationship between fog concentration and scene depth

d(x)∝(v(x)2+(h-s(x))2)min(v(x),0.5)

(8)

为了便于后续运算,文中设定h=1。根据场景深度在近景区域取值较小,远景区域取值较大的规律,使用对数函数估计景深,且能达到扩展灰度值的目的

d(x)=

mln((v(x)2+(h-s(x))2)min(v(x),0.5)+1)

(9)

式中:d(x)表示粗略的场景深度;m表示对数变换系数,用于控制灰度变换幅度。经过大量实验表明,m取1.5更逼近于场景深度。景深变换过程如图4所示。

2.1.2 场景深度优化 利用Meng等的正则化构造加权函数[8],解决相似景深区域透射率相差过大问题,运用到粗略景深的优化,目标函数为

(10)

式中:第一项表示数据项,使精确的场景深度d′和粗略的场景深度d相对平衡;μ表示平衡两者的正则化系数;第二项表示精确的场景深度中相邻像素的关系;ω表示索引集;Wj(j∈ω)为权值矩阵;Dj是一阶微分算子;运算符∘表示元乘算子;⊗表示卷积算子。通过最小化目标函数,可以获得精确的场景深度d′。

为了优化式(10),通过变量分裂法,引入辅助变量γj,从而构造代价函数

(11)

将式(11)变化为

(12)

2.1.3 动态大气散射系数 大气散射系数β表示单位体积的大气颗粒对各方位光线的散射能力,大气颗粒越多,散射能力越强[14]。在多数场景中,β取1。本文对不同的β值做大量实验对比验证,选取具有代表性的几个定值做出对比如图6所示。

由图6可见,当β较小时,恢复图像在近景区域效果较好,而远景区域存在去雾不彻底现象,反之亦然。因此,雾图中雾浓度越大,景深越大,大气散射能力越强,即大气散射系数与场景深度呈正相关。

(a)有雾图像

(a)有雾图像 (b)初步构造景深 (c)粗略的景深 (d)对数变换图图4 场景深度变换过程及相应的对数变换图Fig.4 Scene depth transformation process and corresponding logarithmic transformation diagram

(a)有雾图像

(a)有雾图像

据此,本文提出了动态散射系数对不同景深选取不同的β值,以提高整体去雾效果。由于散射系数与图像的细节无关,利用精确的场景深度求取局部平均操作,消除纹理效应,保持散射系数的局部恒定性;再通过指数函数和平均景深构造大气散射系数的表达式

(13)

式中:da(x)表示平均深度信息;d′(x)表示精确的场景深度;N表示图像局部块中包含的像素个数,δ取0.001,为了防止对数运算的结果趋于负无穷,并采用联合双边滤波使其平滑

β(x)=(1-exp(-da(x)))2+mean(d′(x))

(14)

式中,mean(·)表示取均值。通过深度信息的均值反应雾图的整体亮度和指数函数的可调控性,以控制动态大气散射系数的分布。

结合精确的场景深度和动态大气散射系数可以获得最终的透射率,表达式为

t(x)=exp(-β(x)d′(x))

(15)

2.2 大气光值估计

大气光值A是大气散射模型中的一个重要参数,其决定了恢复图像的视觉效果。文献[6]采用暗通道图像中亮度最大的前0.1%的像素点,所对应的有雾图像中的最高强度的像素值选取为大气光值;文献[8]对有雾图像进行最小值滤波直接选择亮度最高的像素值作为大气光值。但是,这两种方法都容易受到高像素值区域的影响,出现误差。文献[10]使用四叉树算法对大气光值进行估计,但易受噪声干扰。文献[15]利用形态学操作消除有雾图像中大面积的白色物体估计大气光值。为了更准确地估计大气光值A,本文基于局部大气光方法[16]提出了改进方法,避免局部区域大气光值过小,造成图像偏亮或偏色现象。具体步骤为:

(1)计算有雾图像的亮度图,利用中值滤波去除噪声和削弱高亮像素点的干扰;

(2)对步骤1的结果图像进行闭运算,保持图像局部特性;

(3)使用亮度图对步骤2的结果图进行联合双边滤波,以消除块状效应,得到初级局部大气光Al(x);

(4)通常情况下,局部大气光A(x)的值不大于有雾图像中像素的最大值,即

(16)

(5)估计A(x)的区间为

(17)

式中:φ表示调节参数,其范围为[0,1],对初级局部大气光Al(x)中的所有像素点取均值作为φ的值。由于φ是与局部大气光分布关联的参数,因此具有自动调节大气光取值的功能。

局部大气光A(x)优化效果对比,如图7所示;与各算法对比结果,如图8所示。可以看出,本文所提方法的局部大气光恢复效果更好。

(a)有雾图像

(a)有雾图像

2.3 图像复原

将最终透射率t(x)和局部大气光值A(x)代入式(1),可以恢复出无雾图像

雾图 Zhu Meng Ren Cai 本文(a)景深突变区域场景

(18)

式中:t0为透射率下限,设置为0.1,以避免分母趋于0及恢复图像出现颜色失真。

3 实验结果及分析

本文实验平台的操作系统为64位Window7,程序运行环境为Matlab R2016a,硬件环境为Intel(R)Core(TM)i5-6300HQ CPU@2.30 GHz,8 GB内存。为了验证本文方法恢复的有效性,使用大量图像在主观和客观方面进行对比分析。

3.1 主观评价

目前较为经典的去雾方法主要有Zhu等人的颜色衰减先验算法[6]、Meng等人的边界约束算法[8]、Ren等人的多尺度卷积神经网络算法[11]及Cai等人的端对端去雾网络算法[12]等。采用本文方法与上述4种算法在不同场景下进行对比,实验效果如图9所示。

由图9a可见:各算法都能恢复出较多细节,但是Zhu算法在景深交替区域存在残雾现象,且整体去雾不彻底;Meng算法牺牲了图像色彩保真度,存在偏色现象;Ren算法在近景处因过饱和而颜色偏暗,出现颜色失真;Cai算法去雾不彻底,图像整体偏暗;本文算法具有良好的色彩保真度,在近景区域颜色更真实自然,色彩鲜艳,景深突变处无残雾,景物细节丰富,整体效果也更好。

在图9b包含天空区域或明亮区域场景下,Zhu算法基本去除了雾气,但存在强光源时会影响大气光值的估计造成图像过于偏暗现象;Meng算法整体上能够恢复图像的细节,但是天空区域严重的颜色失真且存在伪影;Ren算法整体效果较好,但是对蓝色区域的处理有所欠缺;Cai算法的天空区域有较好恢复效果,但相较于其他算法去雾不够彻底;本文算法在视觉效果上占据一定的优势,基本恢复了图像细节,保留了天空特征,且高像素点区域不会造成大气光值的误判,景深突变处过渡自然,无残雾现象,但浓雾图像处理效果并没有达到最佳。

从图9d的薄雾区域中,5种算法都能有效地去除雾气,但是Zhu算法对大气光值估计的不足,造成图像偏暗;Meng算法存在相似问题,颜色较Zhu算法更暗;Ren算法和Cai算法对于颜色保真度都表现得较好,但是两者对于远景区域复原力度不够,前者在还残留着些许雾气,后者去雾不彻底,细节不够突出;本文算法在各部分的去雾都较彻底,恢复出了更多的细节,景深交替处也获得很好地效果。

3.2 客观评价

结合客观评价进一步分析,避免主观评价存在片面性。使用无参考的图像质量评估方法[5],利用图像对比度(CG,用RCG表示)、视觉对比度(VCM,用MVC表示)、通用质量指数(UQI,用IUQ表示)和运行时间(T)作为恢复图像的客观评价指标。其中,RCG体现了图像的色彩程度,RCG越大,图像对比度就越高;MVC体现了图像的可视度,MVC越大,图像就越清晰,这两个指标越大越好;IUQ反应了恢复图像与有雾图像的结构相似性,IUQ越大,与有雾图像的结构相似度就越高,T反应了算法运行速度,这两个指标越小越好。图像对比度和视觉对比度计算公式如下

(19)

(20)

表1为图9的客观评价指标均值对比,从图像对比度可以看出,本文算法基本上获得了良好的效果,但相较于Ren算法有所不足;从视觉对比度测量可以看出,本文算法与其他算法具有一定的优势;通用质量指数表明本文算法有些许优势,与Ren算法效果相近;从运行时间可以看出,由于Zhu算法使用训练样本获取的固定参数,在运行时间上占据优势,但是本文相较于其他算法,具有明显优势,更具实时性。综合考虑,本文方法在去雾效果上相对更好。

表1 5种算法的客观评价指标对比Table 1 Comparison of objective indexes of five algorithms

本文还采用Choi等提出的雾度密度检测方法[18]对图9的所有图像进行检测分析,雾度密度值越小,表明雾气的存在性越小。通常来说,薄雾图像和浓雾图像的区分主观上是通过人眼对图像信息和细节可见度来区分的;客观上使用图像的亮度和饱和度进行判断,亮度越高,饱和度越低,雾越浓;反之亦然。

5种算法的雾密度检测对比结果如表2所示。由表2可见,本文算法在不同雾浓度场景下的图像去雾效果都较好,相较于其他经典算法总体上雾度更小,具有明显优势。

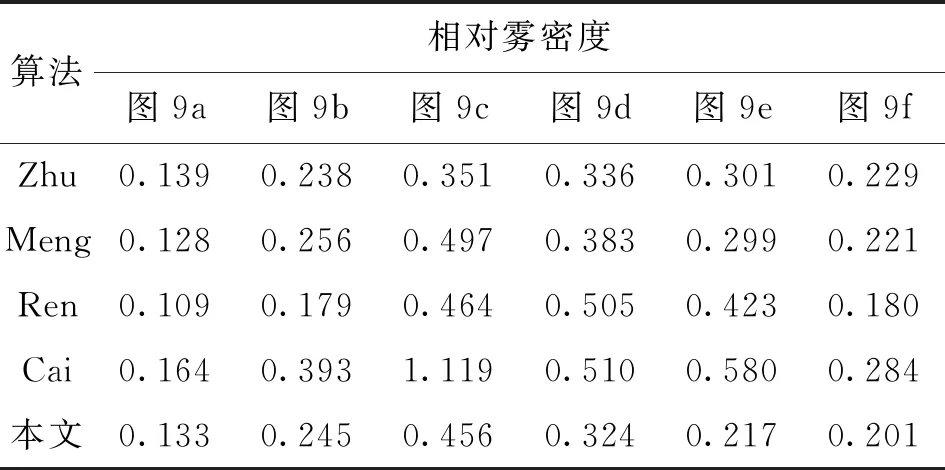
表2 5种算法的雾度密度检测结果对比Table 2 Comparison of haze density detection results of fire algorithms

4 结 论

针对图像去雾中透射率估计不准确问题,本文提出一种结合自适应亮度变换不等式估计透射率的图像去雾方法。首先,使用亮度变换不等式和对数变换进行双调节满足景深变化趋势,估计粗略的场景深度;其次,采用正则化平滑场景深度,获取精确的场景深度;之后,使用局部平均深度估计动态散射系数,加以最大值像素点对局部大气光进行区间优化;最后,恢复出无雾图像。实验结果表明,本文算法的自适应参数调节对图像取得了较好的效果,有效降低了算法复杂度,对薄雾图像能获得良好的去雾效果。同时,各项客观指标占据一定优势,表明本文算法能够获得较好的色调保真度。然而,本文算法在部分图像会出现过饱和现象,例如薄雾和浓雾区域变化特别剧烈的情况,导致亮度和饱和度的整体变化有一定的差异,影响景深估计,还有待进一步研究和改进。