平面接触运动干摩擦阻尼器的微滑移数值模型
2021-06-07蔺彦虎秋朋园汪久根张靖
蔺彦虎,秋朋园,汪久根,张靖
(1.浙江大学机械工程学院,310027,杭州;2.台州学院航空工程学院,318000,浙江台州;3.浙江双环传动机械股份有限公司传动研究院,318000,浙江台州)
由于结构简单、对复杂载荷的耐受性及高温环境中的稳定性能,干摩擦阻尼器被广泛引入薄壁旋转结构减振,起到明显效果。例如,航空篦齿封严结构、高速旋转薄壁齿轮以及航空发动机的叶-盘系统,均是干摩擦减振技术的应用[1]。随着机加工技术的发展,叶-盘系统有被整体叶盘取代的趋势。从减振角度来看[2],整体叶盘失去了榫槽、凸肩、楔块、拉筋等结构,无法提供干摩擦阻尼效应,叶片工作中的振动将加剧。通过对整体轮盘开凹槽安装阻尼环[2]等方法,运用接触表面相对运动产生的干摩擦阻尼效应达到减振目的。
干摩擦阻尼器结构简单,但设计性能优异的干摩擦阻尼器却有较大难度。原因是,结构振动过程中,摩擦接触表面的黏滞-滑移-分离运动状态难以确定,以及干摩擦力对这些运动状态的非线性依赖。一旦干摩擦力无法准确求解,就无法评估其阻尼效应,从而对干摩擦阻尼器的结构和安装参数设计带来困难。因此,研究者们提出了不同的干摩擦阻尼器模型,以逼近阻尼器的真实运动-摩擦力关系,同时一些研究用数值方法确定阻尼器的运动状态[2]。
干摩擦模型起始于符号库伦模型,Hartog研究了含有该模型的单自由度振子,得出封闭解[3]。Buyucataman用库伦模型建模,以摩擦能耗最大化为优化目标,为薄壁齿轮阻尼环安装参数设计提供了理论依据[4]。随着研究的深入,人们逐渐意识到,库伦符号模型不能描述触点滑动之前的弹性形变,因此不能准确预测结构振动结果。于是,研究者将一根弹簧串联于库伦模型,用弹簧的形变描述滑移之前的弹性变形,这样阻尼器模型就由库仑模型进化为滞后弹簧元模型。Griffin用滞后弹簧元模型计算了凸肩叶片的振动,发现计算准确度得到了显著提高[5]。串入弹簧使得触点的滑移、黏滞和分离不仅依赖于法向力,还依赖于触点和其牵引点的运动历程,文献[6-7]对滞后弹簧元模型空间运动的力-位移关系做了深入研究。
以上研究是以一个接触点对描述整个阻尼器的接触运动,称为宏滑移模型。宏滑移模型适合描述法向力均布、幅值较小,且结构和阻尼器刚性均较好的情形。对于薄壁结构,存在较大法向力时,阻尼器有可能在整体滑移之前,在接触面局部发生滑移,这时若仍用宏滑移模型描述运动,将不符合运动接触的实际,给减振运算带来较大误差。针对这种情况,文献[8-9]采用一维运动微滑移解析模型为干摩擦阻尼器建模,计算了结构频响,并分析了与宏滑移模型相比计算结果异同的原因。
一维解析模型的缺点是对法向力分布形式和时变性的限制,阻碍了其运用推广。针对这一情况,文献[10-11]采用解析分析和数值离散相结合的方法,将一维微滑移模型发展为适用于法向载荷时变,并考虑阻尼器整体滑移的情况[10]。文献[12]将干摩擦阻尼器模型发展至三维空间,但其运动状态的求解须同结构振动结合起来,求解中假设接触运动的谐波数量要求较少,否则容易出现收敛问题。李琳系统总结了干摩擦减振模型的发展历程,并提出结构减振计算应向高保真和新型干摩擦阻尼器模型设计方向发展[2];文献[13-14]分别尝试涂层干摩擦阻尼器的切、法向刚度模拟和微滑移接触生热及磨损问题,对干摩擦接触特性进行了进一步拓展。
已有微滑移数值模型将阻尼器视为一维运动,这种近似忽略了2个因素:①阻尼器本体在正交方向上的弹性耦合;②激励点在阻尼器上的具体作用位置。如果两正交方向的激励处于同一位置,尚可简化近似:将激励合成在一个新的方向,并且不计耦合效应;若激励处于不同位置,则会产生较大误差。
本文针对一维数值模型的上述限制,将接触运动由一维扩展至平面运动,同时考虑阻尼器在正交方向的刚度耦合,提出了求解三维接触运动的微滑移数值模型,并用数值跟踪方法分析接触点的黏滞、滑移和分离等现象。
1 三维运动微滑移模型的建立
图1a所示为平板状干摩擦阻尼器。Fz为法向载荷,可在阻尼器不同位置呈不同分布,可以是时变的,即Fz=Fz(D,t),D为位移向量,t为时间。为计及阻尼器自身柔性,将阻尼器离散,使用有限元模型对其进行划分,并获取其刚度矩阵K。用ABAQUS建模,运用Matrix Generate和Matrix Output命令,导出阻尼器刚度矩阵K[15],也可自行编制有限元程序,积分获得其刚度矩阵。在接触运动面,将滞后弹簧单元布置在有限元网格节点,如图1b所示。单元一端的小箭头代表与配对接触面的接触点,称为触点;另一端点固连于节点,称为牵引点。在动力学计算中,使用这些触点表征面接触的动力学行为。

(a)法向力作用面
滞后弹簧元刚度Kd由Hertz接触理论结合有限元网格密度确定,表示触点沿正交两方向的无耦合刚度,因此2×2矩阵Kd仅在对角线上有非零值且两值相等。
滞后弹簧元具有如下式特点
(1)
式中:F表示触点干摩擦力向量;μ为干摩擦系数;Fz取值大于0具备实际意义;X为牵引点的位移向量。由式(1)可知,在法向力作用下,牵引点位移量较小时,触点不滑移,干摩擦力随牵引点位移线性增长;当牵引点位移达到一定量时,弹簧元不再伸长,干摩擦力达到极值,触点开始出现滑动行为。
2 三维运动微滑移模型的求解方法
2.1 单触点运动的轨迹跟踪求解法
微滑移模型虽有大量滞后弹簧元,但各元的运动和摩擦行为都遵从式(1),因此求解微滑移模型的接触运动-干摩擦力行为,需先掌握单个滞后弹簧元的位移历程和干摩擦力求解方法,即轨迹跟踪方法。单触点轨迹跟踪方法最早由Sanliturk提出,但未阐述其求解机理[16]。单颖春应用类似方法,结合时-频算法,计算了航空发动机带凸肩叶片的频响,取得了很好的效果[17]。
图2给出了轨迹跟踪求解可能发生的黏滞、分离及滑移3种可能状态,其中下标i,i+1,…,i+5表示离散时间点,向量U、V分别为牵引点和摩擦触点的位移向量。如图2所示,假设在ti时刻,牵引点位置在U(ti)、触点位置在V(ti);在ti+1时刻,牵引点运动至U(ti+1)位置,这时触点将停滞在以U(ti+1)为圆心、μFz(ti+1)/|Kd(ti+1)|为半径的摩擦圆上,停滞于摩擦圆上的具体位置可通过最小能耗原理得知。触点从V(ti)移动至V(ti+1),最小能耗为
(2)
式中:D(ti)=U(ti+1)-V(ti),表示ti+1时刻牵引点位置与ti时刻触点的位置差(见图2)。求解时间间隔取至足够小时,可认为法向力Fz在ti至ti+1时段内匀速变化或保持不变,这样式(2)可写为
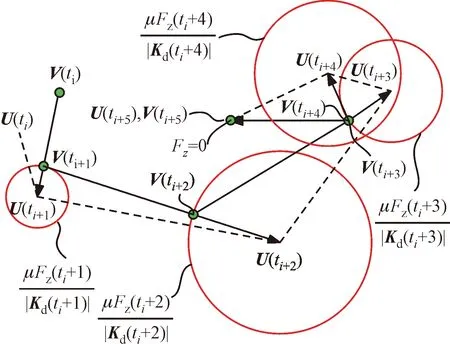
图2 触点运动轨迹求解原理Fig.2 Principle of trajectory tracking method
(3)
触点将滑动至V(ti)与U(ti+1)的连线上,求解连线和该摩擦圆的交点,即可得到触点位移。
依据上述原理,求解时只需知道摩擦圆半径、牵引点位置及触点上一时刻的位置,即可得出当前时刻触点位移和运动状态。如图2所示,假设ti+2时刻,牵引点继续运动至U(ti+2),同样依据最小能耗原理,触点将滑移至V(ti+1)与U(ti+2)的连线并停滞于以μFz(ti+2)/|Kd(ti+2)|为半径的摩擦圆上;当牵引点由U(ti+3)运动至U(ti+4)时,ti+4时刻的摩擦圆覆盖了触点在ti+3时刻的位置V(ti+3),这时触点将处于黏滞状态,从而V(ti+3)与V(ti+4)重合;当牵引点由U(ti+4)运动至U(ti+5)时,法向力为0,所以摩擦圆覆盖面积为0,这时触点将回弹至牵引点,与其重合。同理,逐步计算即可求得触点的整个位移历程。当牵引点运动和法向力呈周期特征时,将形成稳定的位移-干摩擦力滞回环。
2.2 三维接触运动-摩擦力求解流程
求解三维接触运动-摩擦力需得知阻尼器自身刚度矩阵K,并标定滞后弹簧元序号。设定接触运动坐标系x、y方向为接触运动方向,z方向为法向力作用方向,求解时间离散,形成时间步。激励可分为位移激励和力激励,两种类型算法略有不同,但基本求解思想都是寻求不同接触运动状态下的平衡解。本文算法以位移激励类型为例。
触点黏滞-滑移和分离的判定是阻尼器的位移-摩擦力求解的依据,因此对触点运动状态及转化条件进行梳理,如表1所示。

表1 触点运动状态及转化条件Table 1 Transforming conditions of the kinematic state
表中第1列E、S、I分别表示黏滞、滑移和分离状态,法向力Fz代表法向力大小,方向由其符号决定,可写为标量格式。
求解流程如下。
(1)将2×2对角矩阵Kd组装于摩擦面相应节点对应自由度上,形成总刚矩阵Ksum。即将Kd的x和y两分量加至K相应节点自由度上(相应节点自由度由接触面节点序号确定,两分量将添加至K的对角线上)。
(2)假设U1=0,V1=0,F1=0,下标“1”代表求解时间步i=1,还假设触点处于全黏滞状态。
(3)应用矩阵右除法,在给定位移激励增量下,求解平衡方程KsumΔU=0,得到各状态向量增量ΔU、ΔF、ΔV。
(4)Ui+1=Ui+ΔUi,Vi+1=Vi+ΔVi,Fi+1=Fi+ΔFi。
(5)依据表1所列判定条件,检查各触点运行状态是否满足黏滞-滑移和分离状态转换条件,如满足,则根据式(1)修正对应状态向量Ui+1、Vi+1、Fi+1,标记对应触点黏滞-滑移和分离状态,转至步骤(6);如触点运动状态未发生转化,则返回步骤(3)继续下一时间步的求解。
(6)对总刚矩阵Ksum做如下调整:若ti+1时刻,某触点由分离或滑移转向黏滞,则Ksum应在对应节点自由度的主方向(对角线)加上滞后弹簧元的刚阵Kd;若ti+1时刻某触点由黏滞转为滑移或者分离状态,此时滞后弹簧元刚度失效,应将Ksum对应节点自由度主方向减去Kd;若ti+1时刻触点运动状态与i时刻相同,则对Ksum不做调整。
(7)判断求解时间节点是否完成,完成则求解完毕,未完成则返回步骤(3)。
需要注意,总刚矩阵Ksum是一个变量矩阵,其值随触点的运动状态转化而发生相应变化。当所有触点处于滑移、分离或滑移-分离混合状态而无黏滞触点时,滞后弹簧元将全部失效,这时Ksum将退化为奇异矩阵,条件数Cond(Ksum)过大,导致矩阵的右除计算无法进行;这时不再进行矩阵右除运算,而用滞后弹簧单元的性质和单触点跟踪原理确定各状态向量的值:如ΔU和ΔV与激励点位移增量相等,ΔF则由上一时刻的F结合ΔU、ΔV共同确定。另外,为了保证求解中矩阵右除计算的数值稳定性,算法规定当某一时刻处于黏滞状态的触点数量小于等于2时,可认为所有触点处于全滑移或滑移-分离混合状态,从而不再进行右除运算,而是按照上述修正方法确定各状态向量。这样就解决了大条件数矩阵除法运算的数值稳定性问题。经验证,求解结果与不进行这样处理计算得出的求解结果相差不大。
3 算 例
3.1 算例1
平板干摩擦阻尼器材料为65Mn,表面经淬火处理,弹性模量E=20 700 MPa,泊松比λ=0.27。阻尼器为规则长方体,长、宽、高分别为50、30、1.2 mm。在模型长、宽、高方向分别布置11、7、2个节点,划分单元,其刚度矩阵整理为462×462。
模型法向载荷及激励点位置如图3所示。载荷分布为Fz=9+0.15(x-25)2N,Ly=0.13sin(t+π/4)mm,Lx=0.11sin(t)mm,分别为平面内y和x方向的位移激励。

图3 法向载荷形式与激励位置Fig.3 Normal load type and location of excitation
模型接触面含77个节点,在每一节点布置滞后弹簧单元,见图1b,弹簧元刚度为500 N/mm。图4小红点①~表示后续接触运动图及运动-干摩擦力图绘制时(图5、图6、图8和图9)所选择的触点。
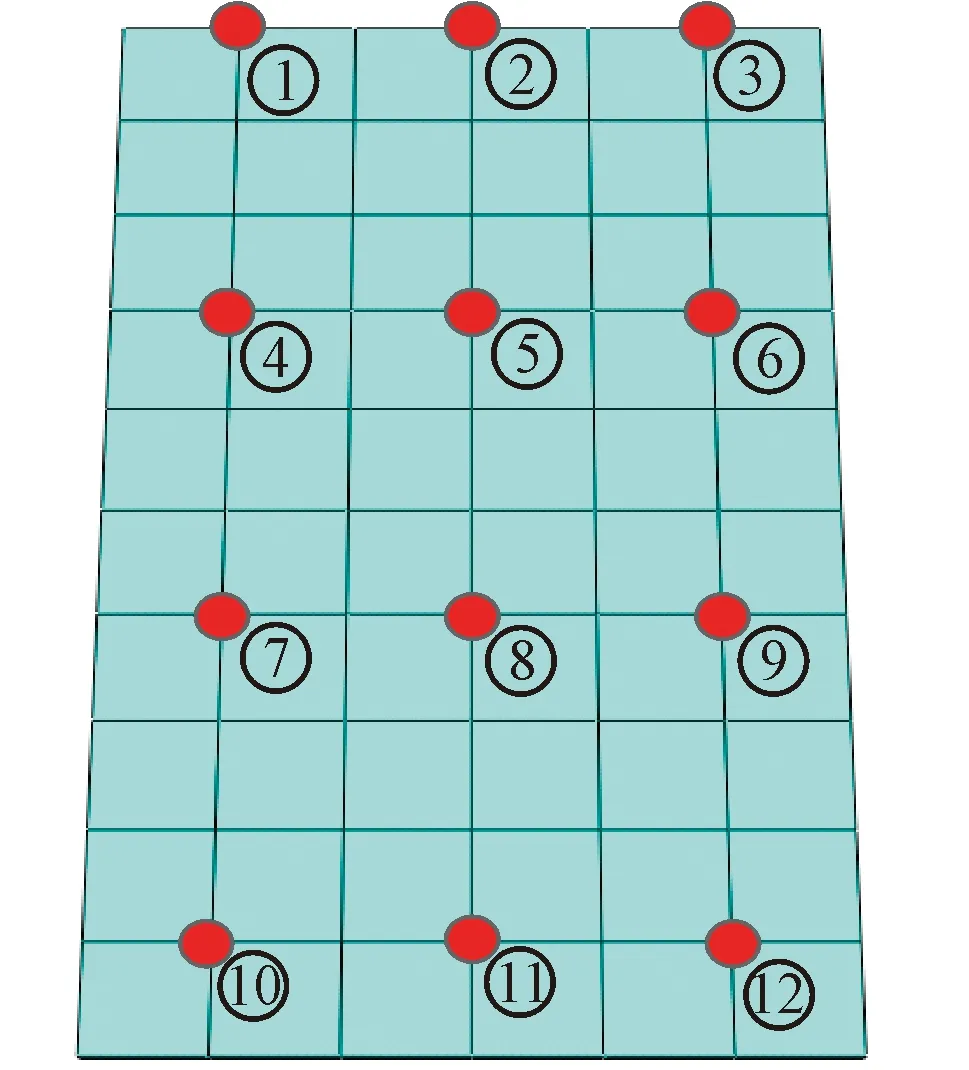
图4 运动历程及摩擦力触点Fig.4 Contact nodes for demonstration

图5 触点平面运动历程Fig.5 Trajectories of the contact points with planar motion
如图3和图4所示:x、y两方向激励位于阻尼器正中心位置,法向载荷也关于x、y轴对称,因此位于阻尼器中间位置的节点更趋向滑动,且关于阻尼器中心呈对称特点;两端法向力大且远离激励点,因此更趋向黏滞;与阻尼器本身刚度相比,触点刚度较小,且阻尼器中参与滑移的节点数量较多(滑移时触点刚度失效),与各触点对应的牵引点位移轨迹主要由激励位置和阻尼器本身刚性决定,仅有微小差异,图中不易看出。
在稳定状态下,图4所示各触点x、y方向的位移-干摩擦力滞回曲线见图6。未滑移的触点干摩擦力呈线性特点;而参与滑移的触点,依滑移程度呈现出环状滞回曲线。该曲线由阻尼器柔性,接触面切、法向刚度,法向力及激励大小、位置共同决定,其围成的面积代表触点运动周期的干摩擦能耗。在结构附加干摩擦减振过程中,阻尼器的滑移部分可提供阻尼效应,而黏滞部分增加了结构刚度,起到一定的调频作用。

图6 部分触点位移-干摩擦力滞回曲线Fig.6 Hysteresis loops of dry friction force versus displacement
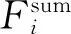
(4)

(a)总滞回曲线
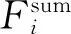
3.2 算例2
算例1两方向激励位于同一节点,在阻尼器中心位置。算例2将x、y两方向激励施加于图3蓝色箭头,Lx=0.2sin(t)mm,Ly=0.14cos(t)mm,其他参数同算例1,得到图8所示的触点位移历程曲线和图9所示的位移-干摩擦力滞回曲线。图中显示了触点跟踪历程,可以看出,达到稳定滞回所需跟踪周期较算例1多了1个。算例2的x方向激励位于阻尼器右端(如图3所示),且激励幅值较大,由于阻尼器两端法向力较大,导致两端接触位置更趋向黏滞状态;靠近激励点位置的滞回环更加饱满,阻尼器呈部分滑移状态。从图8还可看出,阻尼器自身柔性和干摩擦位移历程相关性共同促成触点和跟踪点的位移协调,最终形成稳定运动轨迹。该稳定轨迹不依赖于求解初始位置,这和单触点模型的滞回特性是一致的[17]。
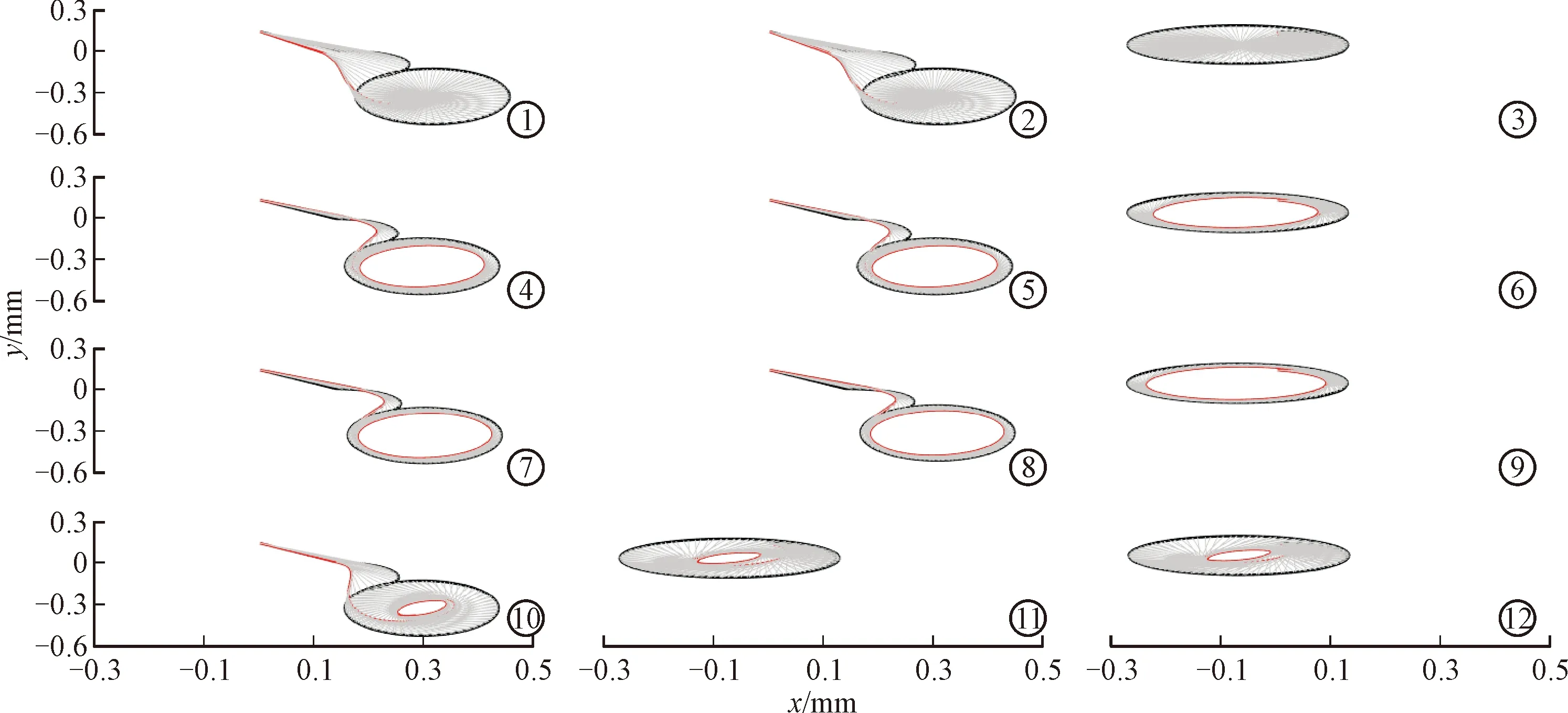
图8 触点平面运动历程Fig.8 Trajectories of the contact points with planar motion: exm.1
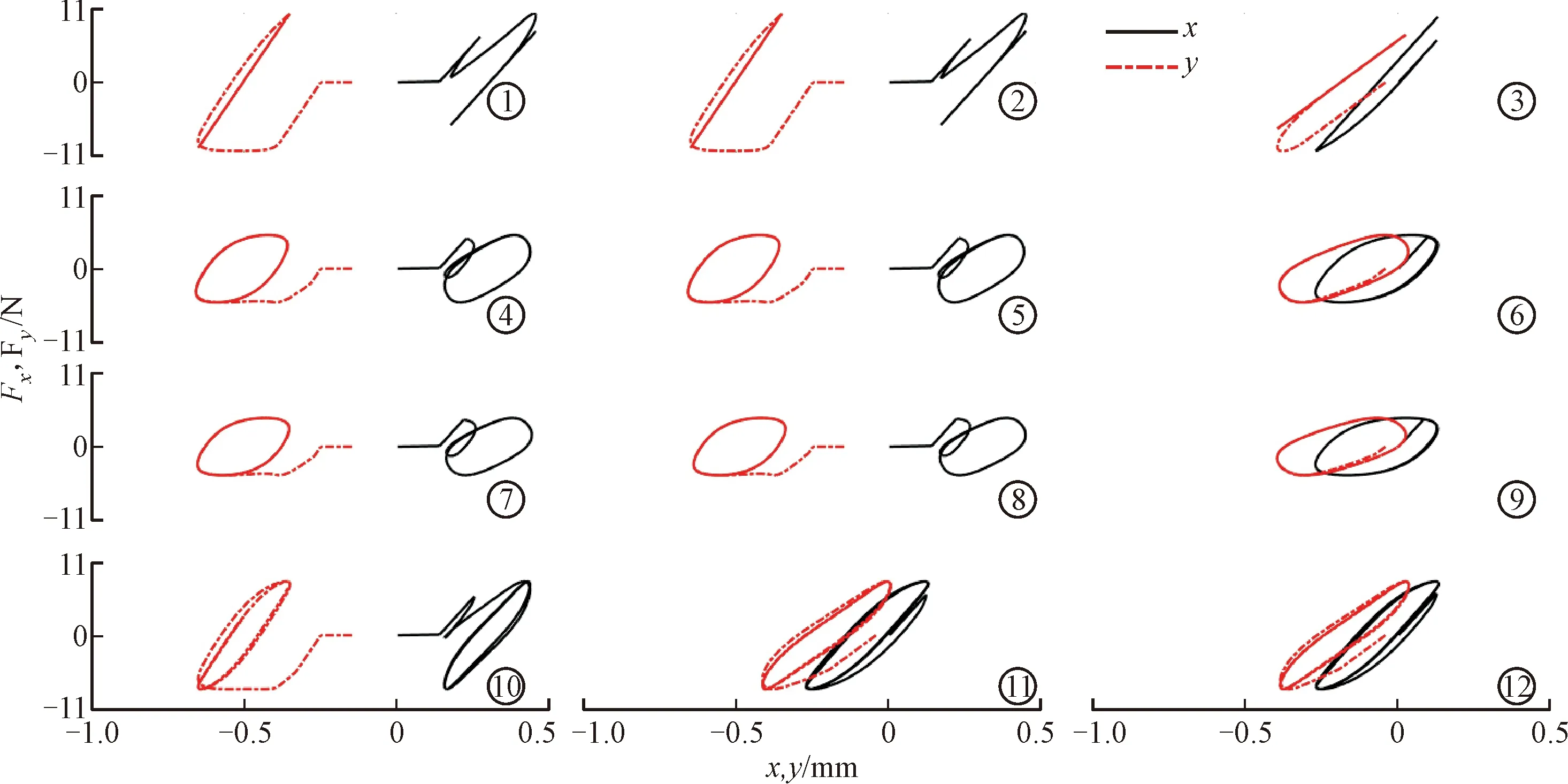
图9 位移-干摩擦力滞回曲线2Fig.9 Hysteresis loops of versus dry friction force displacement: exm.2
求解过程是在时间历程上逐点求解,然后对触点运动状态逐个判定,因此该求解流程还可计算法向力时变情况、多点激励状态以及阻尼器分离状态。当法向力时变时,牵引接触运动状态变化较多,轨迹较难稳定,一般需要3至5个周期。
4 模型在结构频响分析中的应用
4.1 带凸肩叶片振动模型与求解方法
可将图10所示叶片与凸肩减振结构简化为如图11所示的正交二自由度结构,质量为M,x、y方向的刚度和阻尼分别为Kx、Ky、Cx及Cy。该正交2自由度系统控制方程为
(5)

图10 凸肩接触示意图Fig.10 Contact configuration of blades

图11 凸肩叶片2自由度模型Fig.11 2-degree of freedom model of a shrouded blade
式中:Fx(x,y)、Fy(x,y)为干摩擦力,是x、y的函数,x、y方向的运动通过阻尼器产生相互影响;P1和P2表示两方向激励力幅值。
如图10所示,干摩擦阻尼器固连于M质量块,法向力Fz与叶片y向相对位移关系为
Fz=Fz0+Kzysin(β)
(6)
式中:Fz0为初始法向力大小;Kz为阻尼器法向接触刚度;β角为凸肩接触角。
计算所需结构参数和阻尼器参数见表2。阻尼器结构和材料参数同前。

表2 计算所需阻尼器参数和模型参数Table 2 Model parameters and damper parameters for calculation
式(5)含有强边界非线性因素,采用混合时频法(HTF)[18]求解该问题。其求解思路是,先将激励、位移、干摩擦力进行傅里叶变换表示在频域中
(7)
式中:s(t)表示x(t)、y(t)、Fx(t)、Fy(t)、P1(t)、P2(t);Sk表示X(k)、Y(k)、Fx(k)、Fy(k)、P1(k)、P2(k)是s(t)为变量对应的第k阶傅里叶系数;ω和t分别为激励频率与时间;h为计算所取傅里叶级数的最高阶数。这样,可将式(4)写为
ΛkXk-Pk+Fk(x0,y0,…,xh,yh)=0
(8)
式中:Λk=-(kω)2M+jkωC+K,Λk为动刚度矩阵。进一步将式(7)写为如下格式
Γ(X)=ΛX-P+F(X)
(9)
HFT方法的求解流程如下:
(1)对式(8)的谐波系数X进行快速傅里叶逆变换(IFFT),得到x、y方向的位移历程;
(2)依据步骤(1)得到的位移序列计算干摩擦力;
(3)对干摩擦力序列进行快速傅里叶变换(FFT),得到表示干摩擦力的傅里叶谐波系数Fk;
(4)依据上步得到的Fk计算式(8),如果未收敛(足够接近0),则用Broyden方法迭代生成新的X,返回步骤1继续计算,若收敛,则计算下一频率点。
4.2 求解结果及对比
为考察阻尼器本身柔性对减振效果影响,提出等效模型。等效模型用单触点代替接触面,刚度Kx=Ky=38 500 N/m,这时阻尼器退化为宏滑移模型。干摩擦阻尼器带来附加刚度,对结构起到调频作用,使两方向固有频率上升至2 710 Hz。围绕其固有频率进行3种法向力下的微、宏滑移模型的频响分析,x方向结果如图12所示,y方向的计算结果与x方向相仿。

图12 宏、微滑移模型振动频响结果Fig.12 FRF results of macro- and micro-slip model
如图12所示,距离固有频率较远的频率点,振动幅值小,阻尼器不易滑动,阻尼器提供了附加刚度,有利于抑制振动。当法向力较小时,随着计算频率向固有频率靠近,结构振动幅值的增加使阻尼器出现滑移现象。滑移一方面使滞后弹簧失效,为系统一定程度上起到调频作用,另一方面为系统提供干摩擦阻尼,起到减振效果。当法向力较大时,对于宏滑移模型,大的法向力使触点无法滑动,因此无法起到阻尼效应和调频作用,振动峰值计算结果偏大;对于微滑移模型,虽然法向力较大,但阻尼器自身的弹性协调变形使得其局部位置(触点)发生了滑移,起到了阻尼效应,同时起到较小的调频作用,使得频响计算结果较小。在共振频率点,宏滑移模型频响结果为0.049 m,而微滑移模型结果为0.038 m,相差22.4%,由此可见,计算中计入微滑移效应的区别。另外,由图12还可以看出,对于确定幅值的外力激励,存在一个最优法向力,在该法向力下干摩擦阻尼器可达到好的振动抑制效果。
Griffin用宏滑移模型计算凸肩叶片频响,发现接触刚度小、法向力较大时,实验结果小于计算结果,如图13所示[5]。由于不知悉Griffin计算模型参数,无法应用本文改进的阻尼器模型做计算,但可用本文计算结果对计算和实验偏差给出解释:当法向力较小、阻尼器刚度较大时,阻尼器更像是一个刚体,可以用宏滑移模型描述,因此法向力较小时计算与实验结果差异不大;当法向力增大时,阻尼器在整体滑动之前,产生了局部滑移和阻尼效应,抑制了振动;但该计算中使用了宏滑移模型,无法体现局部滑移效应,致使计算值较实验值偏大。
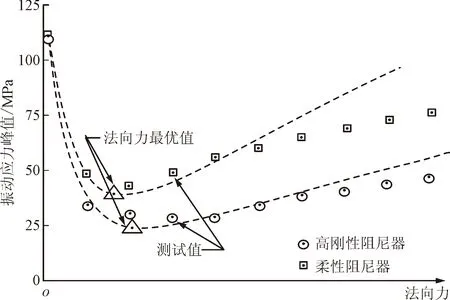
图13 Griffin计算与实验应力结果对比[5]Fig.13 Stress comparison between Griffin’s calculation and test
5 结 论
建立了二维接触运动干摩擦阻尼的数值模型,分别用宏滑移模型和本文改进的模型为带凸肩叶片建模,并分析了两种模型振幅频响异同的原因。
(1)考虑阻尼器自身柔性,将阻尼器离散,在其接触面节点安置滞后弹簧单元,形成干摩擦阻尼器的平面微滑移数值模型。
(2)考虑触点的黏滞、滑移、分离状态和相互转换条件,构建微滑移阻尼器的运动平衡方程,在时间序列上求解该方程,可得到各触点的位移-干摩擦力滞回关系及运动-干摩擦力时间历程。对各触点求和,得到干摩擦阻尼器对外的摩擦约束边界条件。
(3)运用该摩擦模型对含凸肩叶片建模,求解叶片正交方向频响。计算结果表明,微滑移模型的局部滑移可带来阻尼效应,这种效应是宏滑移模型无法预计的。
