含有右半平面零点的宽负载范围DC-DC开关变换器参数设计

2021-06-07皇金锋任舒欣

西安交通大学学报 2021年6期

皇金锋,任舒欣

(1.陕西理工大学电气工程学院,723001,陕西汉中;2.陕西省工业自动化重点实验室,723001,陕西汉中)

随着能源危机的日益突出,光伏和燃料电池等新能源技术已成为当今的研究热点[1-2]。在新能源系统中,需要能在宽负载范围内具有良好暂态和稳态性能的升压型DC-DC变换器,而这些变换器的控制变量到输出电压的暂态数学模型含有一个或多个右半平面(RHP)零点,称之为非最小相位系统[3-7]。RHP零点的存在会导致变换器占空比发生突变时输出电压出现负调现象,负调会导致系统暂态过渡时间延长,且在负调电压持续时间阶段内系统容易形成正反馈而出现不稳定现象[8-9]。因此有众多的科技工作者坚持不懈地探索提高非最小相位DC-DC变换器暂态性能的方法。

文献[4]提出采用改进滞后电流控制来提高非最小相位Boost变换器暂态响应速度。文献[5-6]提出采用滑模变结构控制策略来提高非最小相位DC-DC变换器的暂态性能。文献[8]提出采用改进峰值电流控制方法来提高Boost变换器暂态响应速度。文献[10-11]提出采用磁集成技术来改善RHP零点对Boost变换器暂态性能的影响。文献[12-13]提出采用补偿网络优化方法来提高含有RHP零点的非最小相位变换器的暂态响应速度。文献[14]提出采用固定占空比的控制方法来抑制RHP零点对系统暂态性能的影响。文献[15]提出采用史密斯预估器来抑制RHP零点对系统暂态性能的影响。文献[16]提出一种三态Boost变换器电路拓扑结构来抑制RHP零点对系统暂态性能的影响。以上方法在一定程度上改善了含有RHP零点DC-DC变换器的暂态和稳态性能,但是这些方法实现起来较复杂。由非最小相位开关DC-DC变换器的暂态数学模型可知,RHP零点与变换器参数有关,因此可探索通过对变换器参数的合理设计来抑制负调电压,从而提高系统的暂态性能[17]。然而,目前关于从变换器参数优化设计角度来改善含有RHP零点开关DC-DC变换器的暂态性能的文献较少,尤其是变换器工作在宽负载范围内如何进行参数设计还缺乏相应的理论依据,因此,迫切需要研究宽负载范围内变换器的参数优化设计,以便更好地指导非最小相位开关DC-DC变换器产品的开发与研制。

Buck-Boost变换器是一个典型的非最小相位开关DC-DC变换器,具有电路拓扑简单,可工作在宽输入电压范围等优点,已在新能源等系统中得到了广泛的应用。文献[18]给出了一定输入电压和负载电阻动态范围内Buck-Boost变换器参数设计方法,但未充分考虑到电感、电容和负载电阻对Buck-Boost变换器暂态性能的影响,因此无法指导宽负载范围变换器的参数优化设计。宽负载范围Buck-Boost变换器如果全动态范围工作在电感电流连续导电模式(CCM),需要的电感量太大,会导致系统暂态性能很差,同时出现严重的负调现象而导致系统不稳定;如果全动态范围工作在电感电流不连续导电模式(DCM),则需要的电感量较小,可以提高系统暂态响应速度。但由于含有RHP零点的Buck-Boost变换器电路拓扑的特殊性,若电感量设计太小,会增加输入电源直通发生的可能性,导致电感峰值电流、开关管电压应力和系统的纹波电压非常大。因此,对工作在宽负载范围含有RHP零点的Buck-Boost变换器而言,全动态范围既不能工作在CCM,也不能工作在DCM,参数究竟如何设计是宽负载范围Buck-Boost变换器参数设计的关键。

为此,本文以含有RHP零点的Buck-Boost变换器为例,依据负调电压暂态数学模型中的负调电压峰值时间与变换器电感和电容等参数之间的关系,以及宽负载范围内负调电压峰值时间的极值情况,得出了宽负载范围变换器参数设计的方法,最后进行了仿真和实验验证。研究结果同样适用于其他非最小相位开关DC-DC变换器,对工作在宽负载范围含有RHP零点的DC-DC变换器参数设计具有指导意义。

1 变换器的暂态性能分析

Buck-Boost变换器电路拓扑如图1所示。图中,R为电阻,L为电感,C为电容,D为二极管,Q为开关管。工作在CCM的Buck-Boost变换器输入电压Vi、输出电压Vo和占空比D之间的关系[18]为

图1 Buck-Boost变换器电路拓扑Fig.1 Circuit topology of the Buck-Boost converter

(1)

Buck-Boost变换器CCM又可分为完全电感供能模式(CISM)和不完全电感供能模式(IISM)。Buck-Boost变换器CCM和DCM的临界电感LC以及CISM和IISM的临界电感LK分别为

(2)

式中:f为功率开关管Q的工作频率。

假设Buck-Boost变换器的输入电压工作范围为[Vi,min,Vi,max],负载电阻工作范围为[Rmin,Rmax],则在R-Vi平面上,变换器的工作范围对应一个矩形[18],如图2所示。

图2 在R-Vi平面展开的CISM与IISM分界Fig.2 Boundary between CISM and IISM on R-Vi plane

根据式(2)可画出CISM与IISM的临界电感LK曲线(L1～L4),如图2所示。由式(2)可知,图2中A、B和C点对应的临界电感分别为

(3)

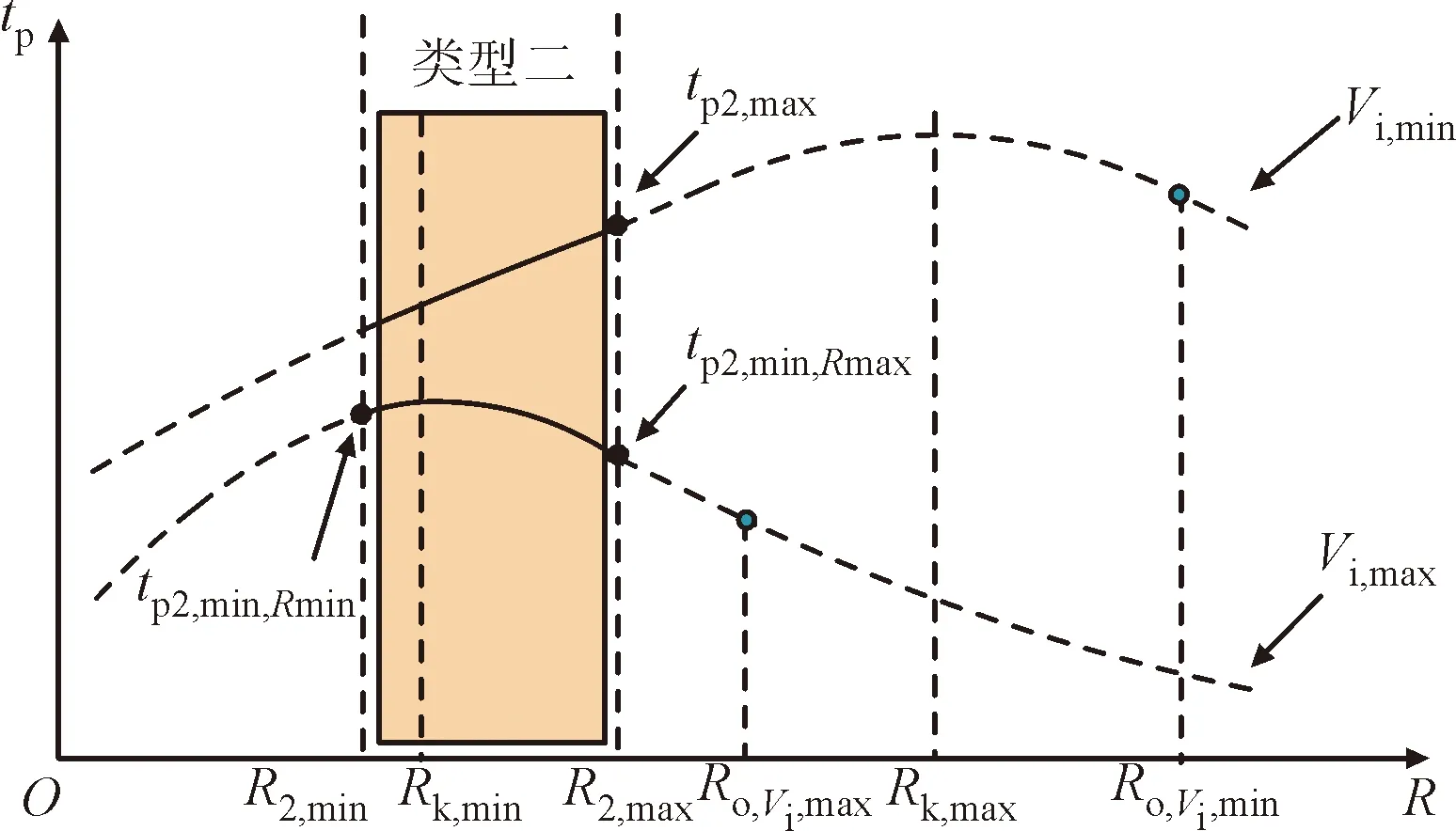
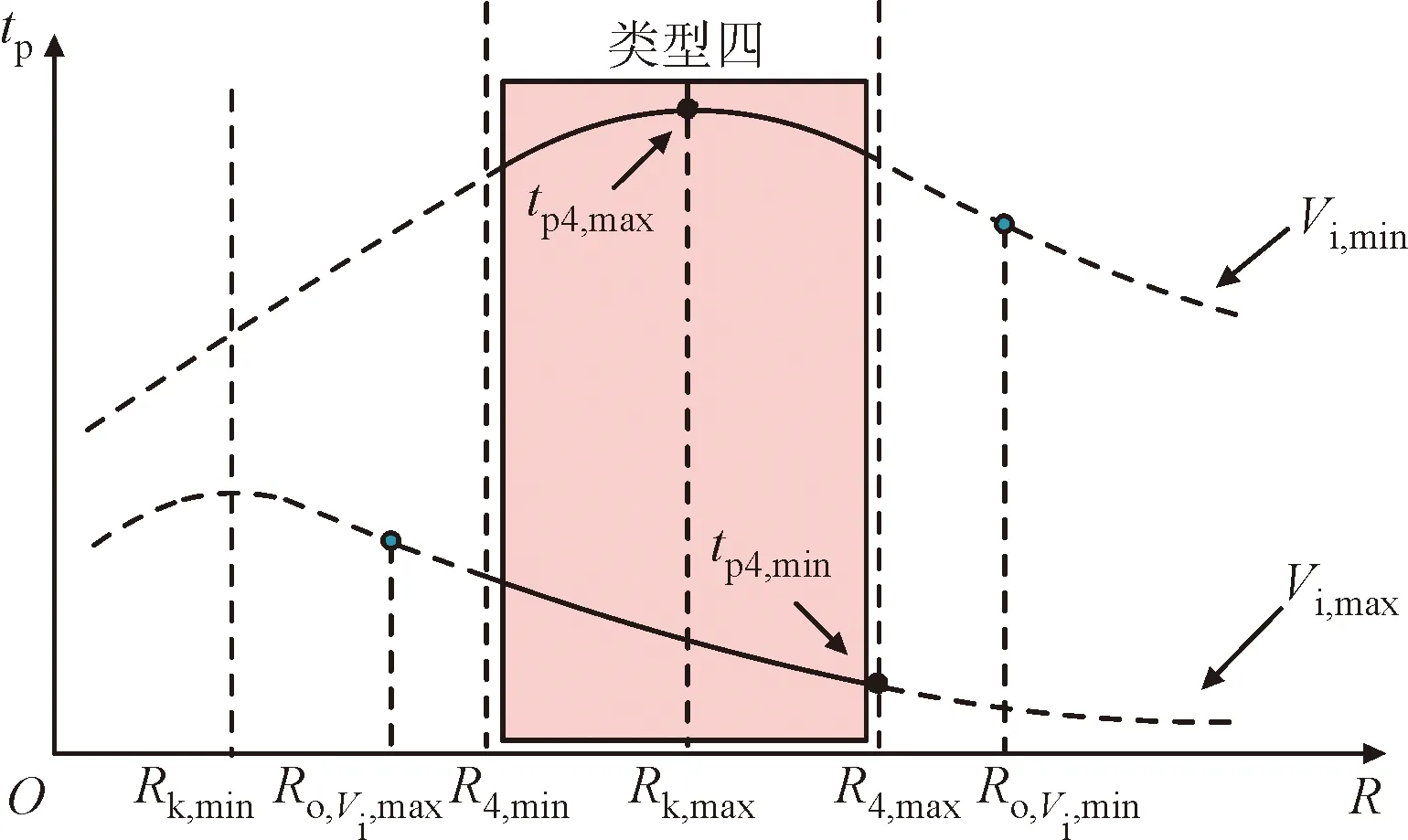
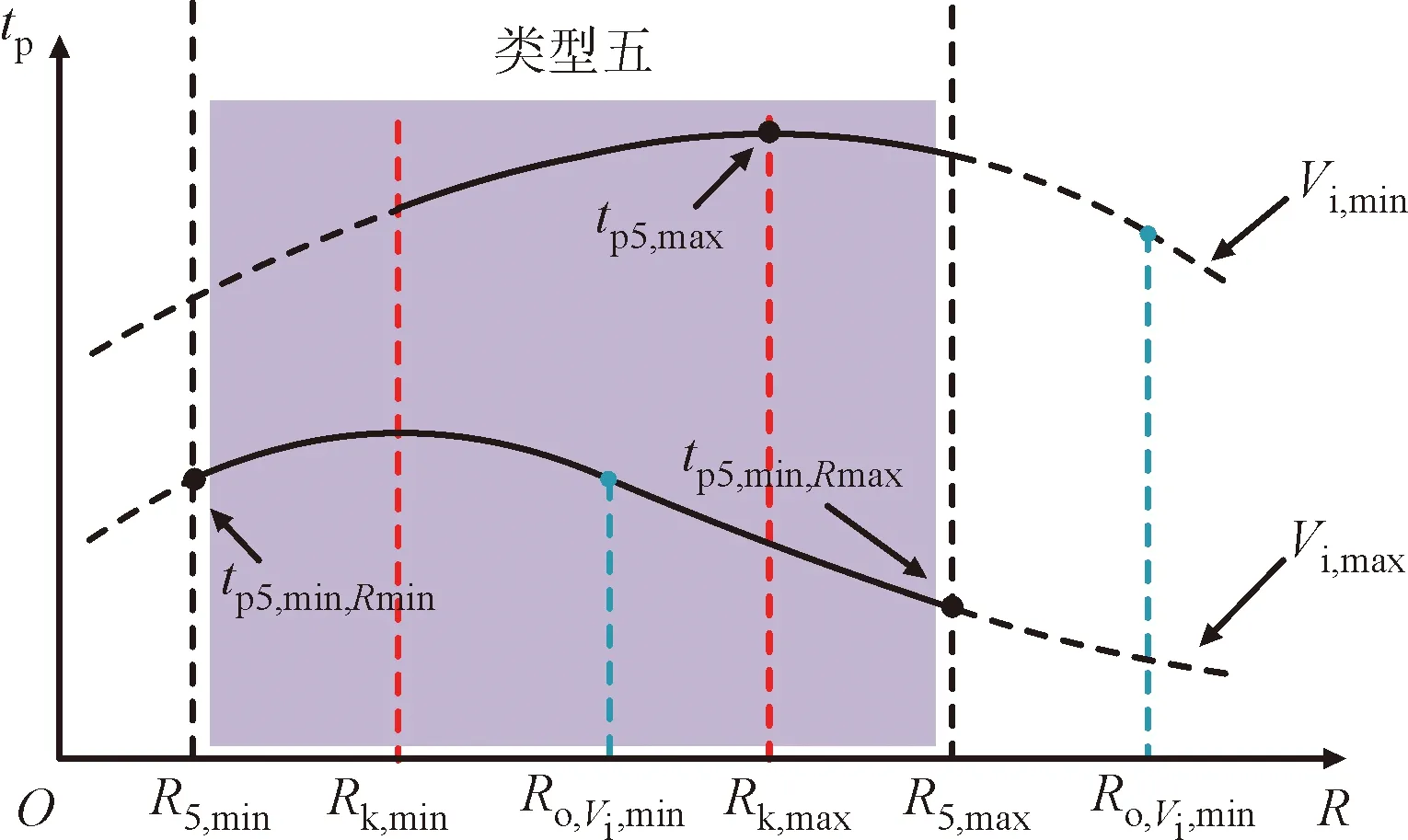
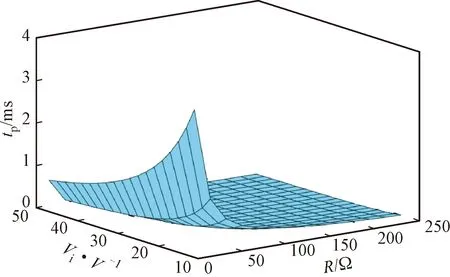
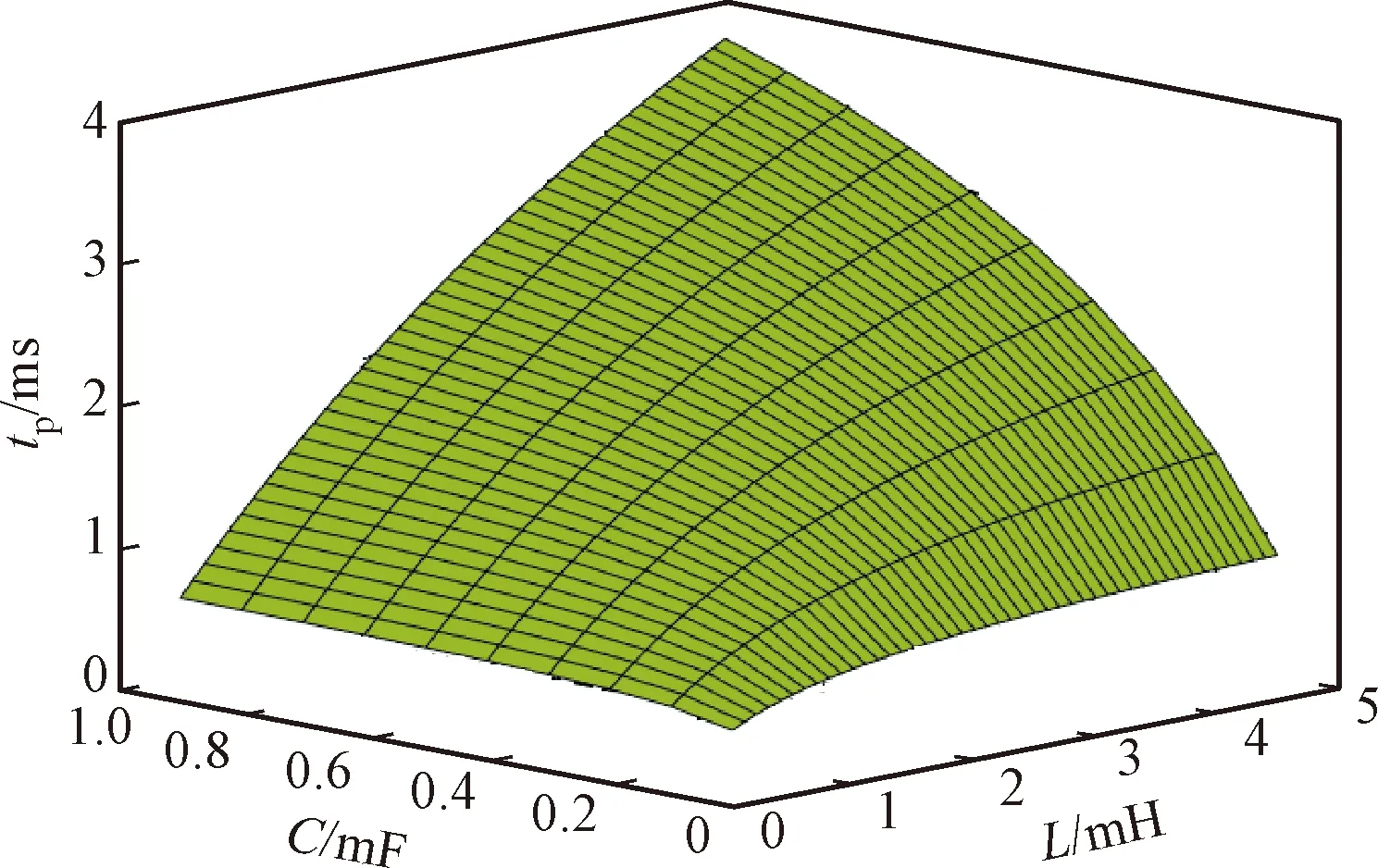
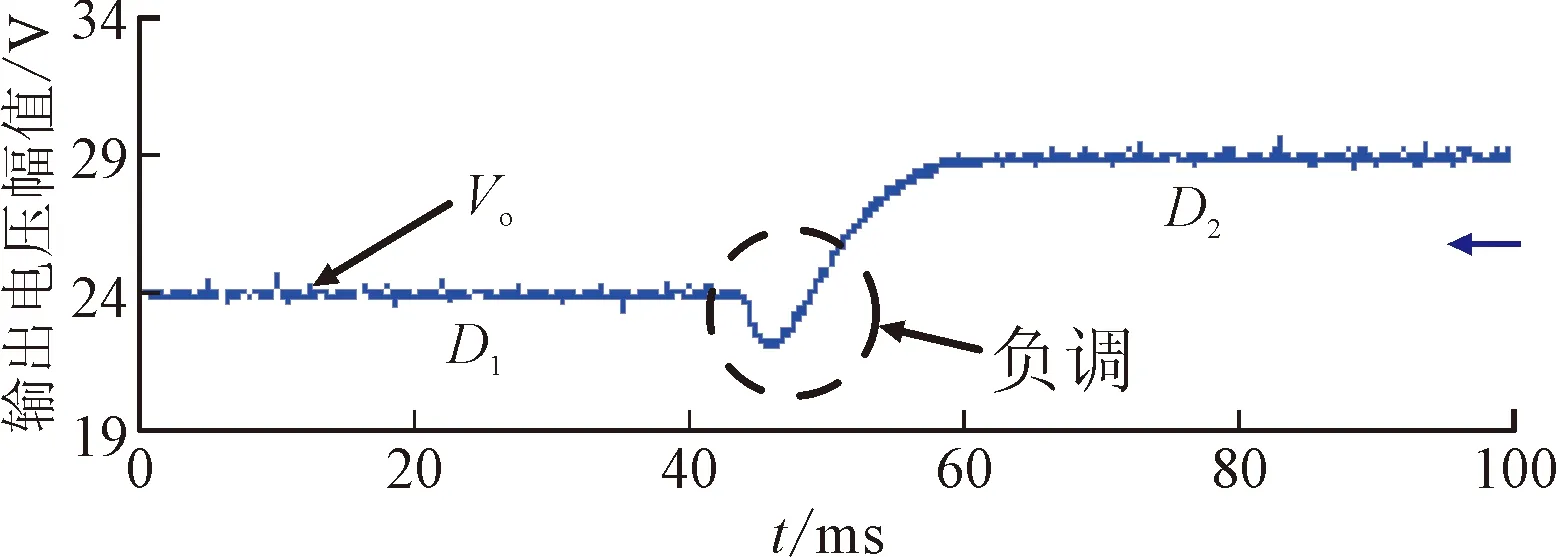
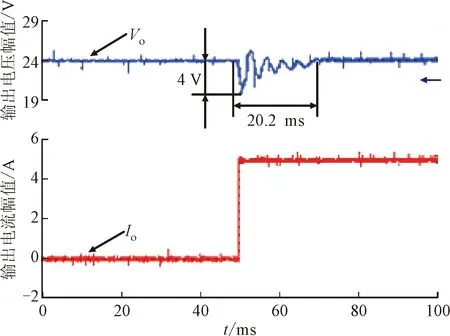
分析式(3)可知,LKC>LKB>LKA。结合图2可得,在该动态范围内,当电感L>LKC时,Buck-Boost变换器在整个动态范围内工作在CISM,对应图2中L1的情形;当LKB

当电感满足L>LKC时,Buck-Boost变换器全动态范围内工作在CISM,此时变换器输出电压纹波Vpp和功率开关器件上的电流应力较小,但所需电感量较大;当电感选择满足L

(a)电压波形

分析图3可知,当占空比发生突变时,Buck-Boost变换器输出电压的暂态过渡过程出现了严重的负调电压现象。负调现象导致系统暂态过渡过程时间延长,在负调现象持续阶段,系统会反馈给输入端错误的电压信号,易出现正反馈现象,导致系统不稳定。因此,宽负载范围的非最小相位变换器全动态范围内不能工作在CISM。

由以上分析可看出,对于工作在宽负载范围的Buck-Boost变换器,电感选择应满足LKC>L>LKA,但具体电感选择多大,缺乏相应的理论依据。负调电压暂态数学模型是宽负载范围非最小相位Buck-Boost变换器参数设计的理论依据,下面给出负调电压暂态数学模型。

2 负调电压暂态数学模型

由文献[19]可知,工作在CCM的Buck-Boost变换器控制变量到输出电压的暂态数学模型为

(4)

式中:D′=1-D。

由参考文献[20]可知,Buck-Boost变换器负调电压暂态数学模型为

Δvo(s)=

(5)

对式(5)进行拉普拉斯反变换得

(6)

将式(6)对时间t求导数,并令其导数为0,可得负调电压峰值时间tp为

(7)

将式(1)和式(6)代入式(7)化简可得

(8)

由式(8)可知,tp随着R的变化而变化,下面就宽负载范围内tp与R的关系进行分析。

3 宽负载范围负调电压峰值时间极值分析

将式(8)中的tp对R求一阶偏导数可得

(9)

令式(9)等于0可得(Rk为驻点)

(10)

式中:Rk为临界负载电阻。

将式(10)代入式(5)可得系统阻尼比ζ0为

(11)

将式(9)对R求二阶偏导数可得

(12)

令式(12)等于0可得(R0为拐点)

(13)

结合上述分析可知,在负载电阻R=Rk时tp达到峰值,如图4所示。由图4可知,tp在宽负载范围内变化时存在极值。

图4 tp随R的变化关系Fig.4 The relation of tp with R

下面就宽负载范围内tp的极值进行分析。

分析式(10)可知,临界负载电阻Rk在输入电压动态范围[Vi,min,Vi,max]内有极大值和极小值,当Vi=Vi,max时,Rk达到极小值,此时Rk=Rk,min,如式(14)所示;当Vi=Vi,min时,Rk达到极大值,此时Rk=Rk,max,如式(15)所示。

(14)

(15)

由于Buck-Boost变换器所带负载电阻R在一定范围内变化,根据负载电阻范围[Rmin,Rmax]与临界负载电阻范围[Rk,min,Rk,max]之间的大小关系可知,负调电压峰值时间tp的极值存在5种类型。

(1)类型一(R1,max≤Rk,min)。当负载电阻范围满足R1,max≤Rk,min时,tp随着R的变化如图5所示。tp随着R增大而增大,当R=R1,max时tp达到极大值,此时负调电压峰值时间极大值tp1,max为

图5 tp随R与Vi的变化关系(R1,max≤Rk,min)Fig.5 The relation of tp with R and Vi(R1,max≤Rk,min)

(16)

为了获得输入电压Vi对tp的影响情况,将式(8)中的tp对Vi求一阶偏导数可得

(17)

分析式(17)可知,在输入电压动态范围[Vi,min,Vi,max]内,tp随输入电压Vi的增大而减小,极值如图5所示。同时考虑输入电压和负载电阻范围,负调电压峰值时间极大值tp1,max和极小值tp1,min分别为

(18)

(2)类型二(Rk,min≤R2,max≤Rk,max)。当负载电阻范围满足Rk,min≤R2,max≤Rk,max时,tp随着R的变化如图6所示。负调电压峰值时间tp在Vi=Vi,min、R=R2,max时达到极大值tp2,max为

图6 tp随R与Vi的变化关系(Rk,min≤R2,max≤Rk,max)Fig.6 The relation of tp with R and Vi(Rk,min≤R2,max≤Rk,max)

(19)

当Vi=Vi,max、R=R2,max时,tp达到极小值,此时极小值tp2,min,Rmax为

(20)

在Vi=Vi,max、R=R2,max时,tp达到极小值,此时极小值tp2,min,Rmin为

(21)

分析式(20)和式(21)可知,当Rk,min≤R2,max≤Rk,max时,负调电压峰值时间极小值tp2,min为

tp2,min=min{tp2,min,Rmax,tp2,min,Rmin}

(22)

(3)类型三(R3,min≥Rk,max)。当负载电阻范围满足R3,min≥Rk,max时,tp随着R的变化如图7所示。负调电压峰值时间tp随着R增大而减小,并在Vi=Vi,min、R=R3,min时达到极大值,此时极大值tp3,max为

图7 tp随R与Vi的变化关系(R3,min≥Rk,max)Fig.7 The relation of tp with R and Vi(R3,min≥Rk,max)

(23)

在Vi=Vi,max、R=R3,max时,tp达到极小值,此时极小值tp3,min为

(24)

(4)类型四(Rk,min≤R4,min≤Rk,max)。当负载电阻范围满足Rk,min≤R4,min≤Rk,max时,tp随着R的变化如图8所示。负调电压峰值时间tp在Vi=Vi,min、R=Rk,max时达到极大值,此时极大值tp4,max为

图8 tp随R与Vi的变化关系(Rk,min≤R4,min≤Rk,max)Fig.8 The relation of tp with R and Vi(Rk,min≤R4,min≤Rk,max)

(25)

当Vi=Vi,max、R=R4,max时,tp达到极小值,此时极小值tp4,min为

(26)

(5)类型五(R5,min≤Rk,min且R5,max≥Rk,max)。当负载电阻范围满足R5,min≤Rk,min且R5,max≥Rk,max时,tp随着R的变化如图9所示。负调电压峰值时间tp在Vi=Vi,min、R=Rk,max时达到极大值,此时极大值tp5,max为

图9 tp随R与Vi的变化关系(R5,min≤Rk,min且R5,max≥Rk,max)Fig.9 The relation of tp with R and Vi(R5,min≤Rk,min on R5,max≥Rk,max)

(27)

当Vi=Vi,max、R=R5,max时,tp达到极小值,此时极小值tp5,min,Rmax为

(28)

当Vi=Vi,max、R=R5,min时,tp达到极小值,此时极小值tp5,min,Rmin为

(29)

分析式(28)(29)可知,当R5,min≤Rk,min且R5,max≥Rk,max时,负调电压峰值时间的极小值tp5,min为

tp5,min=min{tp5min,Rmax,tp5,min,Rmin}

(30)

4 宽负载范围变换器参数优化设计

4.1 变换器参数对负调电压影响情况分析

分析式(8)可知,tp与R、L和C的取值有关。为了获得这些参数对tp的影响,将式(8)对L求偏导数可得

(31)

将式(8)对C求偏导数可得

(32)

分析式(31)和式(32)可知,电感L和电容C越大,tp越长。较小的L和C更有利于抑制tp,从而提高系统暂态性能。但电容C太小无法满足变换器输出纹波电压要求,下面就宽负载范围内Buck-Boost变换器参数优化设计进行分析讨论。

4.2 宽负载范围变换器参数优化设计步骤

宽负载范围Buck-Boost变换器参数设计步骤如图10所示。满足全动态范围内Buck-Boost变换器的输出纹波Vpp要求的最小电容Cmin为

图10 变换器参数优化设计流程 Fig.10 Flow chart of converter parameter optimization design

(33)

式中:λ的取值为2～3。

满足全动态范围内变换器工作在电感完全供能模式的最小电感Lmin为

(34)

式中:γ的取值为1.2～1.5。

5 仿真及实验验证

本节就宽负载范围变换器负调电压峰值时间tp的极值和参数优化设计方法进行仿真和实验验证。

5.1 仿真分析

下面以一个典型宽负载Buck-Boost变换器为例进行仿真分析,具体参数为:输入电压范围Vi=12～48 V,负载电阻范围R=5～250 Ω,输出电压Vo=24 V,开关频率f=40 kHz,滤波电容C=800 μF。图11给出了tp与输入电压Vi和负载电阻R之间关系的仿真结果。

图11 tp与Vi和R之间关系的仿真结果Fig.11 Simulation result of relation of tp with Vi and R

将以上参数分别代入式(2)、(14)和(15)可得:LK=5 mH(选择1.2倍裕量),Rk,min=1.5 Ω,Rk,max=4.3 Ω,系统全动态范围工作在CISM的最小电感LK,min=5 mH。根据已知负载电阻范围与临界负载电阻范围比较可得Rmin≥Rk,max,即负载电阻范围属于第3节的类型三。由图7可知,当Vi=Vi,min=12 V、R=Rmin=5 Ω时,tp达到极大值,tp,max=3.4 ms;当Vi=Vi,max=48 V、R=Rmax=250 Ω时,tp,min=0.015 ms;仿真结果和理论分析结论一致。由仿真结果还可知,工作在宽负载范围的Buck-Boost变换器,当系统全动态范围设计为CISM时tp较大,不利于提高系统暂态响应速度。

为了方便分析L和C对负调电压峰值时间tp的影响情况,图12给出了Vi=12 V、R=5 Ω、Vo=24 V、f=40 kHz、L=0.5～5 mH和C=0.1～1.0 mF时tp与L和C之间的关系。

图12 tp与L和C之间关系的仿真结果Fig.12 Simulation result of relation of tp with L and C

当Lmin=0.5 mH、Cmin=0.1 mF时,tp达到极小值,此时tp,min=0.375 ms;当Lmin=5 mH、Cmin=1 mF时,tp达到极大值,此时tp,max=3.75 ms。由图12仿真结果可知,tp随着电感L和电容C的增大而增大,仿真结果与公式(31)(32)理论分析一致,即电感和电容越大,系统暂态性能越差。

5.2 实验验证

5.2.1 参数优化设计分析为了验证含有RHP零点的宽负载范围变换器参数优化设计的合理性,以一个典型的Buck-Boost变换器为例进行参数优化设计和实验验证,具体参数如表1所示。

根据表1给出的变换器参数并按照第4.2节给出的步骤进行设计。

表1 Buck-Boost变换器电路参数Table 1 Circuit parameters of Buck-Boost converter

(1)设定功率开关管Q开关频率f=40 kHz。

(2)根据式(33)计算出Cmin=800 μF(选择2倍裕量)。

(3)选择Rmax=250 Ω,根据式(34)计算出Lmin=5 mH(选择1.2倍裕量)。

(4)根据给定的电阻范围计算出临界负载电阻Rk的最小和最大值分别为Rk,min=1.5 Ω,Rk,max=4.3 Ω。

(5)根据给出的负载电阻范围[Rmin,Rmax]与[Rk,min,Rk,max]之间的关系,可知当R=5 Ω、Vi=12 V时tp达到极大值,此时tp,max=3.4 ms。

(6)判断出tp,max≤tp,sd,不满足要求。

由以上分析可知,Buck-Boost变换器工作在CISM的负载电阻范围为5～80 Ω,工作在IISM的电阻范围为80～250 Ω;同时由式(2)可知,此时变换器工作在CCM的电阻范围为5～120 Ω,工作在DCM的电阻范围为120～250 Ω。

对比以上分析结果可知,通过提高功率开关管的工作频率可以扩大Buck-Boost变换器在CCM的动态范围,但开关频率f的提高受控制器、元器件和电磁干扰等条件限制。

5.2.2 实验验证宽负载范围非最小相位开关变换器参数设计不仅会影响系统的开环暂态过渡过程,还会影响系统的闭环暂态过渡过程,因此,实验验证分两个方面,一方面对负调电压抑制前和抑制后的暂态过程进行对比,另一方面验证参数优化前后对系统闭环暂态过渡过程的影响情况。

为了验证理论分析的合理性,搭建了一台Buck-Boost变换器实验样机,功率开关管为IRF640NPBF,功率二极管为MBR20200F,实验平台如图13所示。

图13 实验平台Fig.13 Experimental platform

(1)负调电压暂态特性实验验证。参照表1的变换器参数选择两组Buck-Boost变换器数据进行实验,对比分析占空比突变前后变换器的暂态性能,两组参数分别为:①L=5 mH,C=800 μF,R=5 Ω,f=40 kHz,Vi=12 V,实验结果如图14a所示;②L=200 μH,C=800 μF,R=5 Ω,f=40 kHz,Vi=12 V,对应的实验结果如图14b所示。

将L=5 mH、C=800 μF、R=5 Ω、f=40 kHz、Vi=12 V代入式(23)可得tp=3.4 ms;由图14a的实验结果可看出,此时tp=2.1 ms;将L=200 μH、C=800 μF、R=5 Ω、f=40 kHz、Vi=12 V代入式(23)可得tp=0.2 ms;由图14b的实验结果可看出,由于此时tp非常小,已看不出负调电压现象,达到了抑制负调电压的目的,提高了系统的暂态响应速度。

(a)L=5 mH,C=800 μF

对比图14a和14b的实验结果可知,工作在宽负载范围内的非最小相位Buck-Boost变换器,若全动态范围内工作在CISM,变换器会出现严重的负调电压,系统的暂态性能差;通过对变换器参数进行合理优化设计,可以有效地抑制负调电压,从而提高系统的暂态响应速度。

(2)闭环系统暂态实验验证。为了进一步验证参数优化对Buck-Boost变换器闭环系统暂态性能的影响,参照表1的变换器参数选择优化前后的两组参数进行闭环实验验证。

实验采用电压闭环控制系统,补偿网络参数设计方法见参考文献[20]。优化前的实验参数为:L=5 mH,C=800 μF,f=40 kHz,Vo=24 V,实验结果如图15a所示;优化后的实验参数为:L=200 μH,C=800 μF,f=40 kHz,Vo=24 V,实验结果如图15b所示。图中给出了Buck-Boost变换器稳定工作波形及系统抗负载扰动情况,并将二者的实验结果进行了对比分析。