政府双重监管体制下可再生能源消纳的演化博弈研究

李龙 聂龑 陟晶 张国兴

摘要：日趋严峻的碳排放约束、急剧扩张的可再生能源装机规模以及大规模的“弃风、弃光”行为间相互制约，严重阻碍了我国电力系统的低碳、智能转型。基于政府对发电企业节能减排行为和电网企业可再生能源保障性收购的双重监管，构建电网企业和发电企业间的演化博弈模型，分析三者间的利益冲突与合作过程，进而探究博弈影响因素和协作发展轨迹。研究发现：政府监管力度对企业达标行为具有直接影响，企业达标概率与政府设置的惩罚系数值正相关，其中电网企业对其敏感性更高;通过技术革新降低企业生产成本比单一地提高惩罚系数对提升企业达标积极性具有更好的激励效果。为了强化能源规制政策效果，切实达成预期的减排和消纳目标，我国需从制度上迈出“监管推动发展”的怪圈。政府应结合泛在电力物联网激发企业的创新发展意识和自主达标意识，尽快建立完善的电力市场，并积极引入第三方以降低能源规制的监管成本，最终达到环境友好、能源清洁、智能高效的电力系统转型目标。

关键词：双重监管体制;能源规制;可再生能源消纳;演化博弈

一、引言

随着经济全球化的深入发展和《巴黎协定》碳减排压力的逐步上升，全球电力系统都进入了转型升级的新阶段。[1]国际环境的变化及能源、资源的限制都极大地刺激了我国可再生能源的快速发展，《2018年度全国可再生能源电力发展监测评价报告》指出：截至2018年年底全国风电和光伏装机量分别达到1.84亿千瓦和1.75亿千瓦，占全球装机总量的33%和36%。但因资源禀赋、区域壁垒、机制缺陷以及主体间的利益冲突等问题，导致可再生能源的消纳量远不及装机量，每年都会产生大量的“弃风、弃光”，2018年新疆和甘肃地区的“弃风、弃光”率总和高达38.4%和28.8%。可再生能源消纳不足会严重制约我国能源系统的转型升级，进而危及国家能源安全，约束经济和环境持续发展。

为了确保可再生能源的利用效率，有效协调区域能源发展，2016年国家发改委、能源局依照我国《可再生能源法》要求，核定了重点地区风电和光伏发电最低保障收购年利用小时数，提出全额保障性收购相关要求;2019年两部门又印发了《关于建立健全可再生能源电力消纳保障机制的通知》，要求各地电网企业按配额消纳足量的可再生能源。因此，在节能减排政策约束和可再生能源保障性收购需求下，分析政府、电网企业和可再生能源发电企业之间的利益冲突与合作过程，揭示影响我国能源转型、环境保护和经济发展的关键因素，探究三者之间的演化策略和发展路径就显得至关重要。

碳排放量高会导致全球气候变暖，大力发展可再生能源可以有效抑制碳排放总量。[2]因此，针对可再生能源的研究开始大规模涌现，研究内容主要集中在发电企业内部的技术创新[3]、企业生产结构调整[4]、宏观政策驱动[5]以及体制层面构建碳市场[6，7]等，这些研究旨在通过降低可再生能源的生产成本来增强电力系统的安全性和稳定性。发展可再生能源“消纳”才是决定电力系统可持续转型的关键。电网企業通过天然气发电（PTG）技术[8]、微网技术和储能技术[9]等来均衡电网能量波动，提升可再生能源的消纳率。但可再生能源消纳不仅仅是技术问题，还涉及到区域协调发展的利益均衡以及政策协同等问题。[10，11]

Bhattacharya等[12]建议各国政府、能源规划处、国际合作机构必须共同行动，增加可再生能源投资，以促进大多数经济体的低碳增长。分析相邻两个地区可再生能源投资补贴博弈的福利效应可以获得更优的合作策略。已有学者对此进行了探究，发现“利益归属”是制约可再生能源消纳并网问题的关键，其中，影响消纳的两大责任主体——发电企业和电网企业之间的演化博弈状态主导了可再生能源的发展和利用模式。[13-15]刘秋华等[16]基于贝叶斯博弈理论，提出了一种不完全信息市场交易下多个售电商博弈的定价模型，寻找发电集团间合作的最优策略。Naz等[17]在能源管理体系中制定了两阶段Stackelberg博弈，以协调传统资源和可再生资源的管理。

上述研究利用演化博弈论动态分析发电主体、输配电主体和用电主体之间的利益关系，发现政策补贴、发电配比、定价策略之间的最优组合可以促进可再生能源的发展。但从“减排”和“消纳”两个维度出发，基于能源规制动态分析电力系统演化发展过程中涉及到的多利益主体之间的博弈行为和演化路径的研究还较少。探寻碳减排（“减排”）和可再生能源的保障性收购（“消纳”）间的有效实施路径可以推动国家能源政策的执行;厘清“减排”“消纳”行为主体间的博弈过程和合作方式不仅可以促进电力企业的协同发展，还能加强我国能源系统的安全、稳定发展。

鉴于此，本文构建了一个“减排”“消纳”双重约束的可再生能源消纳演化博弈模型，分析政府监管效力对发电企业和电网企业行为模式的影响。本文结合周德群等[18]和Korkas等[19]的研究引入电网消纳可再生能源和发电企业节能减排的成本函数，并在一个统一的框架下分析了完成不同程度消纳和减排配额对利益主体收益的影响，讨论电网企业和发电企业之间的最优决策行为，以便为政府制定能源环境规制政策提供理论依据。

二、双重监管体制下的博弈模型

在“减排”和“消纳”的双重监管体制下，政策、资源和社会环境都对发电企业和电网企业施加影响，使其在清洁发电和自身利益之间难以抉择，企业很难准确地做出最佳决策。因此，本文利用演化博弈论方法对政府监管下电网企业和发电企业间的协同演化发展问题进行建模分析，将电网企业和发电企业之间的协同演化发展抽象为博弈主体间的利益冲突与合作过程，从而分析各方策略发展轨迹及其演化影响因素。

（一）模型假设与参数定义

考虑我国碳减排政策和可再生能源全额保障性收购政策的制定和执行的具体情形为：发电企业通过技术升级和产业重组来减少单位发电量所产生的二氧化碳，地方政府负责减排配额分配并进行监督检查;政府核定重点地区风电和光伏发电最低保障收购年利用小时数，电网企业需要完成规定数量的可再生能源保障性消纳，在执行期间政府会进行监督检查。然而，地方政府会基于监管成本和自身利益考虑选择监督管理行为的严苛程度，这又导致发电企业和电网企业会存有少减排、少消纳等侥幸行为，若是侥幸行为被政府监察发现将会受到严重的违规经济处罚。

根据上述情景模拟提出如下研究假设：假设电网企业的配额收购量为M1，发电企业的减排要求为M2;企业基于机会主义行为，都存有降低成本不愿达标的动机，电网企业不达标概率为1-α1，发电企业不达标概率为1-α2。假设政府监管部门对企业进行认真检查就一定能够获得其真实的达标情况，其认真检查的概率为θ，检查成本为C（C>0）。γ1w1为电网企业消纳不足时须缴纳的罚金，其中w1为电网企业未消纳电量，γ1为政府监管部门对电网企业未达标的惩罚系数（单位罚金）;同理，γ2w2为发电企业减排不足时须缴纳的罚金，w2为发电企业未完成的减排量，γ2为政府监管部门对发电企业未达标的惩罚系数（单位罚金）。

电网企业和发电企业的正常收益分别为R1和R2。若在政府监管行为发生时双方都未达标，企业除了承担罚款外还需要支付政府监管部门的检查成本，假设电网企业承担比例为β，发电企业承担比例则为1-β;若仅有单一企业未达标，则该企业支付所有检查成本C。仅有单一企业达标，政府将给予达标企业R3奖励;双方企业都达标，政府将给予各R4奖励金额，且R4>R3。不失一般性，假设上述各参数值均大于0。有关参数符号及含义见表1。

由于政府、发电企业和电网企业之间的博弈存在着相互之间的信息不对称，且各自的策略是动态变化的，同时由于政府严苛的监督管理行为是建立在企业未达标的基础上，企业的策略选择也是博弈中要考虑的因素，故本研究的基础模型为不完全信息下政府—电网企业—发电企业间的三方动态博弈，博弈三方通过不断地获取信息，逐步寻求最优策略。

（二）各方收益分析

综合上述假设，考虑不同监管程度下电网企业和发电企业的收益情况。根据已有研究，设定电网企业可再生能源的消纳成本函数为f（x1）=a1x1+b1[20]，电网企业的消纳成本与其消纳量呈线性关系。发电企业减排成本函数为f（x2）=a2x22+b2x2+c2[18]，鉴于“学习曲线”中知识积累、规模效应和投入产出要素价格变动等表现形式都会影响其减排成本，当积累到一定程度时减排成本会下降，发电企业的减排成本函数为开口向下的二次函数曲线。

在电网企业和发电企业都达标且政府监管部门进行认真检查时，政府将自行承担检查成本C，电网企业和发电企业仅需要支付足额的消纳成本a1M1+b1和减排成本a2M22+b2M2+c2，而且政府还会给予电网企业和发电企业各R4的奖励。在仅单一企业达标时，政府会仅给予达标企业R3的奖励（R4>R3），未达标的企业则承担全部检查成本C。结合上述分析，在“减排”“消纳”双重治理的监管体制下，当政府执行较为严苛的监管时，电网企业和发电企业的演化博弈收益矩阵如表2所示。[21]

三、博弈均衡分析

根据政府实施监察管理时电网企业和发电企业演化博弈的收益矩阵，计算电网企业达标和未达标状态下的期望收益函数。电网企業达标状态下的期望收益为dα1di表示在政府监管条件下随着时间的变化，电网企业选择消纳行为达标概率的变化率，其值大于0表示电网企业消纳行为达标的概率随时间的变化不断增加，反之减少。在政府执行较为严苛的监管时，电网企业决定足额消纳时的收益高于其不达标行为的收益，同时高于电网企业的平均期望收益时，对电网企业而言，选择足额消纳策略是对其最为有利的决策行为。所以说，在可再生能源消纳过程中，电网企业应逐渐改变自己的消纳策略倾向足额消纳，以获得最大收益。

与公式（4）相似，dα2di>0表示在监管下，发电企业选择足额减排行为的概率随时间变化不断增加。在政府执行较为严苛的监管时，当发电企业选择足额减排行为时的收益高于其减排不达标时的收益，同时高于其平均期望收益时，对电网企业而言，选择节能减排策略是对自身企业最为有利的行为。所以说，在电力系统节能减排演化过程中，发电企业理应改变策略努力实现足额减排，以获得最优收益。

（一）监管条件下电网企业足额消纳行为的演化稳定性分析

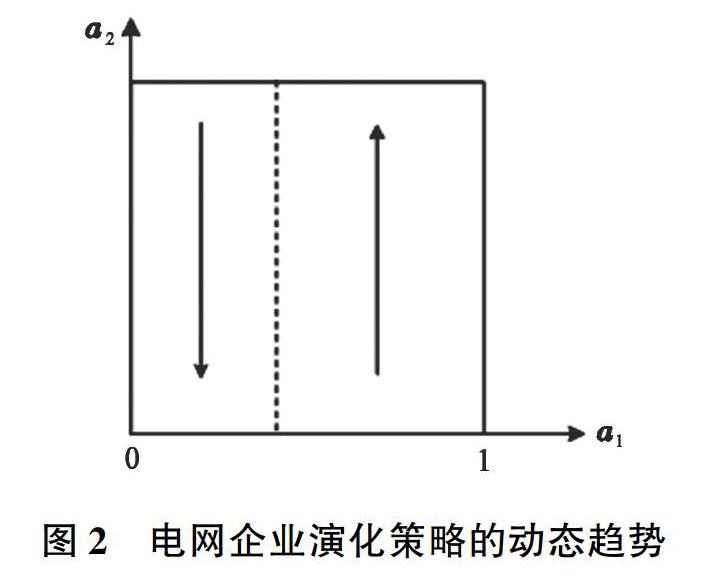
电网企业完成的消纳量与额定量之间的差值越小，且电网企业的惩罚系数大于等于其消纳成本系数值时，电网企业有参与足额消纳演化策略的积极性;完成消纳的量越大，未达标的惩罚系数越高，电网企业完成足额消纳演化策略的积极性越强烈，但当完成消纳的数量远小于额定数量，且惩罚系数远低于消纳成本系数时，电网企业就会由积极参与转为消极应对。

（二）监管条件下发电企业足额减排策略的演化稳定性分析

（三）政府监管下电网企业与发电企业的演化稳定分析

根据电网企业和发电企业演化博弈的复制动态方程（4）和（8），组合得到双重监管体制下的电力系统协同演化策略的动态系统，其中

根据表3分析得出，两个渐近稳定点A和B是该动态系统的演化稳定策略，分别对应于电网企业和发电企业选择（不足额消纳演化策略，不足额减排演化策略），以及电网企业和发电企业选择（不足额消纳演化策略，足额减排演化策略）两种情况。局部稳定点C、D、E反映出系统处于暂时稳定的状态，一旦有扰动因素影响，则会偏离这种暂时稳定的状态。进一步，我们用坐标轴来表示电网企业和发电企业这两个博弈方的演化稳定趋势，如图5所示。

分析图5（a）可知，当电网企业不积极参加足额消纳策略时，对电网企业的惩罚系数小于等于其消纳成本的系数值，同时满足发电企业的惩罚系数无限接近于其减排成本时，系统将收敛于A（0，0），即两个企业均不参加“消纳”和“减排”策略时，整体电力系统的低碳、智能化程度较低。

图5（b）和（c）表明，当发电企业的惩罚系数远小于其减排成本时，无论系统如何演化，最终都将收敛于B（0，1），即发电企业均会选择积极参加协同演化策略。这种情况一般出现在电力系统转型的初始阶段和中期阶段。根据发电企业节能减排成本函数可知，在系统转型初期，其学习曲线带来较高的技术成本，政府给予发电企业的政策支撑较弱时，发电企业的成本将远高于其惩罚系数，为了促进发电企业的节能减排，技术升级和政策支撑是最有效的手段。电力系统逐渐演化，发电企业的减排成本逐渐接近其惩罚系数，整体系统的低碳、智能演化稳步推进。

以上分析表明，可再生能源发电大规模并网的初期，由于相关制度规范缺失，技术、人才配套不到位等原因，生产出的可再生能源电力很难被积极消纳掉。随着电力系统的演化发展，可再生能源电力并网技术逐渐突破瓶颈，电源结构逐步优化，电力市场开始改革，电力政策进一步进行引导监管，最终增加了可再生能源的保障性消纳数量。[22]但是，可再生能源发电大规模并网依然是一个十分复杂的过程，而且在相当长的一段时间内可再生能源电力上网和电网企业之间依然会存在博弈关系。最终可再生能源电力并网将进入协同发展阶段，[23]电网企业借助市场调节机制，优先消纳可再生能源电力;发电企业在节能减排的前提下，还要从内部进行清洁发电技术改革。相关市场機制逐步完善，国家策略从最初的强势控制和补贴引导转变为提供更加完善的市场服务。

四、数值模拟与分析

通过构建政府双重监管体制下电网企业和发电企业之间的博弈模型，分析可再生能源消纳规划和节能减排策略对电网企业和发电企业演化行为的影响方式，得到了两者行为与模型参数间的关联关系。但是，我国尚未对未完成消纳和减排的企业实施具体罚款，也没有形成有效的监管体系，因此，本文对政府监管力度以及惩罚系数的设定进行模拟仿真分析，进一步分析模型的解释意义。

（一）电网企业的消纳成本和惩罚系数分析

根据上述电网企业和发电企业的演化稳定性分析可知，电网企业的收益函数为f（α1）=α1（1-α1）θ{α2（R4-R3+C）+（M1-w1）（γ1-a1）+[R3+（1-α2）βC]}，为了方便对比分析电网企业消纳成本和惩罚系数之间的关系，我们假设α1=β=0.5，θ=1。根据上述假设，可以得到图6所示的电网企业收益与消纳惩罚系数之间关联关系的算例分析图。

如图6所示，随着政府消纳惩罚系数逐渐增大，电网企业的收益率也会逐渐增大。这表明，高比例的惩罚系数对企业行为具有相当大的影响，因此在高比例的惩罚系数下，电网企业更愿意积极消纳可再生能源，完成消纳任务。当消纳惩罚系数与电网消纳成本系数相等时，γ1=a1，电网企业的收益值为32，电网收益达到均衡状态。但在提高惩罚系数的同时，也要考虑电网企业消纳成本系数值，两者之间的差值越小，其收益越低。鉴于此，应通过技术升级和区域电力协调调配来主动提高电网消纳可再生能源电力的灵活性和安全性。综上，在政府较为严苛的监管下，提升电网企业的消纳惩罚系数，同时通过技术创新升级来降低电网消纳成本，可以有效提高电网企业的消纳积极性。

（二）发电企业的减排成本和惩罚系数分析

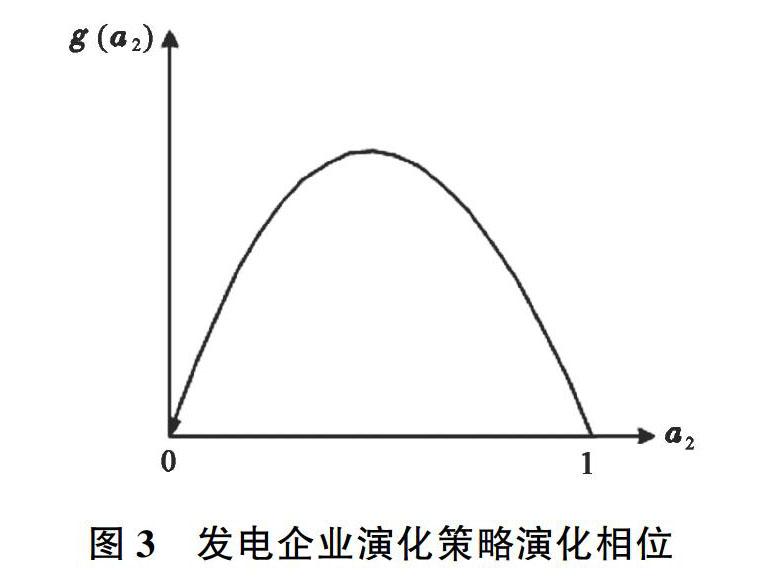
根据上述电网企业和发电企业的演化稳定性分析可知，发电企业的收益函数为g（α2）=α2（1-α2）θ{α1（R4-R3+C）+（M2-w2）[γ2-b2-a2（M2+w2）]+R3+（1-β）（1-α1）C}。为了方便对比两个企业的成本系数和惩罚系数，我们假设α2=β=0.5，θ=1，根据上述假设，可以得到图7所示的发电企业收益与减排惩罚系数之间关联关系的算例分析图。

如图7所示，随着政府减排惩罚系数的增加，发电企业的收益率也出现了增大的趋势。高比例的惩罚系数对发电企业减排行为具有较大影响，在高比例的惩罚系数下，发电企业更愿意积极配合政策引导进行自身节能减排。发电企业的减排成本Cg=a2w22+b2w2+c2，因其具有的学习效应呈现出抛物线的特征，前期0

（三）政府监管力度

我们假设电网企业和发电企业的惩罚系数都取中间值，政府监管力度θ取值区间为[0，0.25，0.5，0.75，1]，可以得到图8和图9所示的电网企业收益和发电企业收益与政府监管力度之间的关系分析图示。

由算例分析可以发现，随着政府监管力度的加大，电网企业和发电企业足额完成消纳和减排的行为都更为积极，相应的企业收益都会变大。这表明，政府监管力度对电力系统低碳、智能转型行为具有更为直接的影响，可以通过加大政府的监管行为来提升企业的环保创新能力。对比图8和图9可知，电网企业的收益值变化对政府监管力度更为敏感，但发电企业具有更大的收益均值。这表明，电网企业对政府监管行为的反应度更灵敏，对其施加政府监管获取的收益值更大。综上，提高政府的监管力度，对双方企业节能减排行为均有影响，其中对电网企业的影响力度更大。

五、研究结论与建议

基于节能减排和能源消纳的双重监管体制，本文构建出电网企业和发电企业间的演化博弈模型，结合监管力度、惩罚系数和成本控制系数等博弈影响因素，分析了双重监管体制下电网企业和发电企业之间的利益冲突与合作过程及其策略发展轨迹。模型均衡分析和仿真研究发现：政府监管力度对企业达标行为具有直接影响，监管力度越大企业达标概率越高;企业的足额达标概率都与其惩罚系数正相关，其中电网企业对惩罚系数的敏感性更高，这与电网企业的成本函数呈现出线性特征紧密相关;在提高惩罚系数的同时降低电网消纳成本和清洁发电成本也可以有效提升企业消纳减排的积极性。

根据以上结论，为促进电网企业和发电企业完成消纳减排任务，进而实现整体电力系统的低碳、智能转型，本文提出如下政策建议：

（1）双重监管体制下，企业节能减排和能源消纳达标的概率与政府对企业行为的检查概率正相关，与政府对其的经济惩罚和激励系数正相关。政府对企业的经济激励与经济惩罚相结合可以有效提升其达标的积极性;而且设置阶梯式惩罚模式比单一标准惩罚系数具有更好的监管效用，这不仅可以减低政府的监管成本，还能从根本上提高企业达标的积极性。

（2）实施技术革新降低成本比单一地提高惩罚系数对提升电网企业和发电企业达标的积极性具有更好的激励效果，因此，技术创新、成本优势依然是促进系统转型的重要途径。但是，随着电力改革纵向推进，配电和用电侧市场竞争日益激烈，电网企业的发展道路愈发狭窄。在此背景下，电网企业的技术创新不能仅从企业自身出发，应结合科技革命和产业变革、并联互联技术，推进“三型两网”建设;强化能源规制政策效果，切实达成预期的减排和消纳目标，从体制上迈出“监察推动发展”的怪圈，通过完善电力市场制度和电网改革来激发企业的创新发展意识和自主达标意识。

（3）降低能源规制的监管成本，通过引入社会公众参与和第三方参与、增加资金投入和人员配备、借助泛在电力物联网技术和大数据技术等手段，提高能源环保部门的监管能力和监管水平，降低企业不达标的预期。

参考文献：

[1] Mcmeekin A， Geels F W， Hodson M. Mapping the Winds of Whole System Reconfiguration： Analysing Low-carbon Tansformations across Production， Distribution and Consumption in the UK Electricity System （1990—2016）[J]. Research Policy， 2019，48（5）：1216-1231.

[2] Stram B N. Key Challenges to Expanding Renewable Energy[J]. Energy Policy，2016，96：728-734.

[3] Verdolini E， Vona F， Popp D. Bridging the Gap： Do Fast-reacting Fossil Technologies Facilitate Renewable Energy Diffusion？[J]. Energy policy， 2018，116：242-256.

[4] Peng X， Tao X. Decomposition of Carbon Intensity in Electricity Production： Technological Innovation and Structural Adjustment in China's Power Sector[J]. Journal of Cleaner Production， 2018， 172（PT.1）：805-818.

[5] Bataille C， Ahman M， Neuhoff K， et al. A Review of Technology and Policy Deep Decarbonization Pathway Options for Making Energy-intensive Industry Production Consistent with the Paris Agreement[J]. Journal of Cleaner Production， 2018，187：960-973.

[6] Zhang S， Andrews-Speed P， Li S. To What Extent Will China's Ongoing Electricity Market Reforms Assist the Integration of Renewable Energy？[J]. Energy Policy， 2018，114：165-172.

[7] Brown M A， Li Y. Carbon Pricing and Energy Efficiency： Pathways to Deep Decarbonization of the US Electric Sector[J]. Energy Efficiency， 2019，12（2）：463-481.

[8] Collet P， Flottes E， Favre A， et al. Techno-economic and Life Cycle Assessment of Methane Iroduction via Biogas Upgrading and Power to Gas Technology[J]. Applied Energy， 2017，192：282-295.

[9] 李美成，梅文明，張凌康，等.基于可再生能源不确定性的多能源微网调度优化模型研究[J].电网技术，2019，43（4）：1260-1270.

[10] Hua Y， Oliphant M， Hu E J. Development of Renewable Energy in Australia and China： A Comparison of Policies and Status[J]. Renewable Energy， 2016，85：1044-1051.

[11] Felix Christian Matthes. Energy Transition in Germany： a Case Study on a Policy-driven Structural Change of the Energy System[J]. Evolutionary and Institutional Economics Review，2017，14（1）：141-169.

[12] Bhattacharya M， Paramati S R， Ozturk I， et al. The Effect of Renewable Energy Consumption on Economic Growth： Evidence from Top 38 Countries[J]. Applied Energy， 2016，162：733-741.

[13] Yang Y， Nie P， Liu H， et al. On the Welfare Effects of Subsidy Game for Renewable Energy Investment： Toward a Dynamic Equilibrium Model[J]. Renewable Energy， 2018，121：420-428.

[14] 李宏仲，王磊，林冬，等.多主体参与可再生能源消纳的Nash博弈模型及其迁移强化学习求解[J].中国电机工程学报，2019，39（14）：4135-4150.

[15] Wang L， Zheng J. Research on Low-carbon Diffusion Considering the Game among Enterprises in the Complex Network Context[J]. Journal of Cleaner Production， 2019，210：1-11.

[16] 劉秋华，何晓敏，冯奕，等.售电侧放开模式下售电商定价方法研究——基于贝叶斯博弈模型分析与应用[J].价格理论与实践，2018（7）：115-118.

[17] Naz A， Javaid N， Rasheed M B， et al. Game Theoretical Energy Management with Storage Capacity Optimization and Photo-Voltaic Cell Generated Power Forecasting in Micro Grid[J]. Sustainability， 2019，11（10）：2763.

[18] 周德群，许晴，马骥，等.基于演化博弈的光伏产业支持政策研究[J].技术经济与管理研究，2018（3）：114-119.

[19] Korkas C D， Baldi S， Michailidis I， et al. Occupancy-based Demand Response and Thermal Comfort Optimization in Microgrids with Renewable Energy Sources and Energy Storage[J]. Applied Energy， 2016，163：93-104.

[20] 舒康安，张昌，艾小猛，等.基于分段电价的跨区风电消纳[J].电工技术学报，2017，32（S1）：39-49.

[21] 吴士健，孙向彦，杨萍.双重治理体制下政府碳排放监管博弈分析[J].中国人口·资源与环境，2017，27（12）：21-30.

[22] 赵昕，朱连磊，丁黎黎.能源结构调整中政府、新能源产业和传统能源产业的演化博弈分析[J].武汉大学学报（哲学社会科学版），2018，71（1）：145-156.

[23] Nie Y， Lv T， Gao J. Co-evolution Entropy as a New Index to Explore Power System Transition： A Case Study of China's Electricity Domain[J]. Journal of Cleaner Production， 2017，165：951-967.

责任编辑：曲 红