高中生物理问题提出能力现状研究
2021-06-06田菁柴志方
田菁 柴志方
摘 要:通过对高中毕业生的问题提出能力的调查发现,高中生在结构化问题情境下的提问更加流畅,但是所提问题更多处于记忆和操作水平,在自由情境下提出的问题则更具有独创性,但是问题的有效性较低.建议在基础教育中融入问题提出的教学策略,可以从结构化问题情境开始对学生进行训练,训练一段时间后给学生提供更多的半结构化或者自由情境,更有利于学生提出具有创造性的问题.教师要具备基本的问题提出能力,同时还应该具有问题提出的教学信念.
关键词:问题提出能力;基础教育;物理教学
中图分类号:G633.7 文献标识码:A 文章编号:1008-4134(2021)05-0002-04
作者简介:田菁(1996-),女,山西晋城人,硕士研究生,研究方向:中学物理教育;
柴志方(1977-),男,河北邢台人,博士,副教授,研究方向:中学物理教育.
教育要培养面向未来的人才,而创新能力无疑是未来人才必须具备的一个特质,能够提出恰当合理且有创造性的问题是创新能力的重要表现.因此,在基础教育中重视培养学生的问题提出能力是非常有必要的.学生在已有知识、经验的基础上进一步提出问题,不仅是对学生所学知识的巩固和应用,更能激发出学生主动去解决自己所提问题的兴趣,学生在内在动力的驱使下会学习更深层次的知识和技能.同时,学生具备问题意识并具备提问的能力是符合《普通高中物理课程标准(2017年版)》(以下简称《标准》)里提出的培养学生科学探究能力的目标[1],科学探究的第一步就是基于实验,观察、发现并提出问题,提出一个结构良好的问题是科学探究的前提.目前我国基础教育中学生问题提出能力的现状如何,又有哪些可以改进的方法,是本文接下来要探讨和解决的问题.
1 物理问题提出能力评价量表的编制
笔者结合国内外研究者对问题提出能力的相关研究,将物理问题提出定义为:“学生在已有物理经验的基础上对具体情境进行个人解释,并从这些情境中提出有意义的物理问题的过程.”
1.1 问题提出能力测试题编制
Stoyanova和Ellerton[2]根据对问题提供的开放性水平区分了三种类型的问题处理情况:结构化情境(structured situations);半结构化情境(semi-structured situations);自由情境(free situations).
(1)在结构化问题情境下,学生可以重新改编已经解决的问题,如改变问题的条件或提问从而形成新的问题.首先,提供给学生一道结构良好的问题,在问题后提示学生改编问题的方法,如改变题目中的条件、结论或者任意数据和信息来重新构建问题,学生如果没有提问的基础,可以根据提示完成問题的改编.
例如,根据一道高中运动学的问题编制问题提出能力测试题目A1,学生解决这道题需要学习自由落体运动相关知识,同时题目中给出了提出新问题的方法,学生可根据提示完成问题提出活动.例如根据一道电场的问题编制问题提出能力测试题目A2.
问题A1:一小球从某高处以6m/s的速度竖直向上抛出,落到地面时速度大小为24m/s,求小球在空中运动的时间.请根据这个题目,通过改变题目中的条件、结论或者任意数据和信息来重新构建问题,尽可能多地提出与物理相关的问题.
问题A2:带负电的两个点电荷P、Q固定在相距10cm的地方,如果将第三个点电荷O放在PQ连线间距A为2cm的地方,O恰好静止不动,则P、Q两个点电荷的电荷量之比为多少,PQ之间距离P为2cm处的电场强度E等于多少?请根据这个题目,通过改变题目中的条件、结论或者任意数据和信息来重新构建问题,尽可能多地提出与物理相关的问题.
(2)在半结构化问题情境下,学生利用已有知识来解释或者构建问题情境,提供给学生开放式问题,并要求学生利用概念和已有知识技能和经验去分析所提供的问题情境,提出类似的问题或根据特定图片、图表提出问题,或者提出与特殊概念有关的问题.
首先给学生提供一个问题情境,如问题B1中的雨天骑车场景和问题B2中的物理实验室场景,但只给出部分的问题条件,而问题中缺少一些必要的条件,学生需要自己对问题情境进行补充,构建形成结构良好的问题.
问题B1:一个下雨的早上,你匆忙骑自行车赶往学校,因为快要迟到了,所以骑得很快,在拐弯处你被摔了出去,你后面的一辆汽车紧急刹车才没有撞到你.请根据这个场景,补充相关数据,尽量多地提出与物理相关的问题.
问题B2:在学校的物理实验室中你想要测量电阻,你想到了哪些方法,由此你可以提出哪些物理问题?
(3)在自由的情境下,学生被要求在给定的人工或自然情况下提出问题,并且可以不受任何限制地提出问题.首先提供给学生问题情境,如问题C1中的水面小船情境,问题C2中的牛顿运动定律概念教学情境,学生被要求补充条件和问题,提出结构良好的问题,据此编制了如下问题.
问题C1:水面上有几艘小船,一艘静止在水面上,一艘在水面上行驶.请补充相关数据,尽量多地提出与物理相关的问题.
问题C2:请根据牛顿运动定律的概念和规律,补充相关数据或情境,分别提出适合初中生和高中生的问题并注明,尽量多地提出与物理相关的问题.
1.2 问题提出能力评价量表编制
国内外关于学生问题提出能力评价的研究更多地集中在基础教育数学学科领域,不同研究者使用的评价体系有一定的差别,还未形成一个公认的、具体可行的评价标准.对学生问题提出能力评价的定量研究中,使用最多的是PTA量表,需要研究者对问题提出能力的概念进行解构,确定每个要素的评价指标和评价标准,并制定评分标准.
流畅性、灵活性和独创性被Xianwei Y、Van Harpen和Presmeg[3]认为是创造力的核心维度.流畅性是指学生提出的可行问题的总数,对学生同一个题目下所提问题的数量进行统计,根据所提问题数量占据总数的比例得出学生提问流畅性的评分;原创性是指如果一个问题是由大于等于10%的学生提出,那么它被认为不是原创的,对学生所提的相同问题进行统计,根据所提问题的人数占总人数的比例得出问题原创性的评分;灵活性是指学生提出的问题类别的总数,问题类别又有不同的区分标准,斯海霞[4]将学生提出的数学问题从记忆与操作、理解与联系、反思与拓展三个维度进行区分,本文以此作为学生所提问题的区分依据.学生所提问题的科学性可以从所提问题是否有效或有意义进行区分,有意义的问题又可以从记忆与操作、理解与联系、反思与拓展三个维度进行区分,这三个维度的难度是逐渐递增的,问题的科学性也递增,反映出的学生提问能力的层次也递增.具体而言,无效或者无意义的问题是指所提问题的结构不完整或者与所给情境不符合或者不属于物理问题等,记忆与操作类问题是指学生对问题所给条件的重复表达而且所提问题的解答过程较为单一,理解与联系类问题是指学生可以将问题材料与生活实际或者相关物理知识技能相联系,反思与拓展类问题是指可以反映问题本质的一般性问题,根据学生所提问题的类别进行评分,问题所属层次越高得分越高.除此之外,对学生所提问题的可解决性以及语言表达的适当性进行评分.
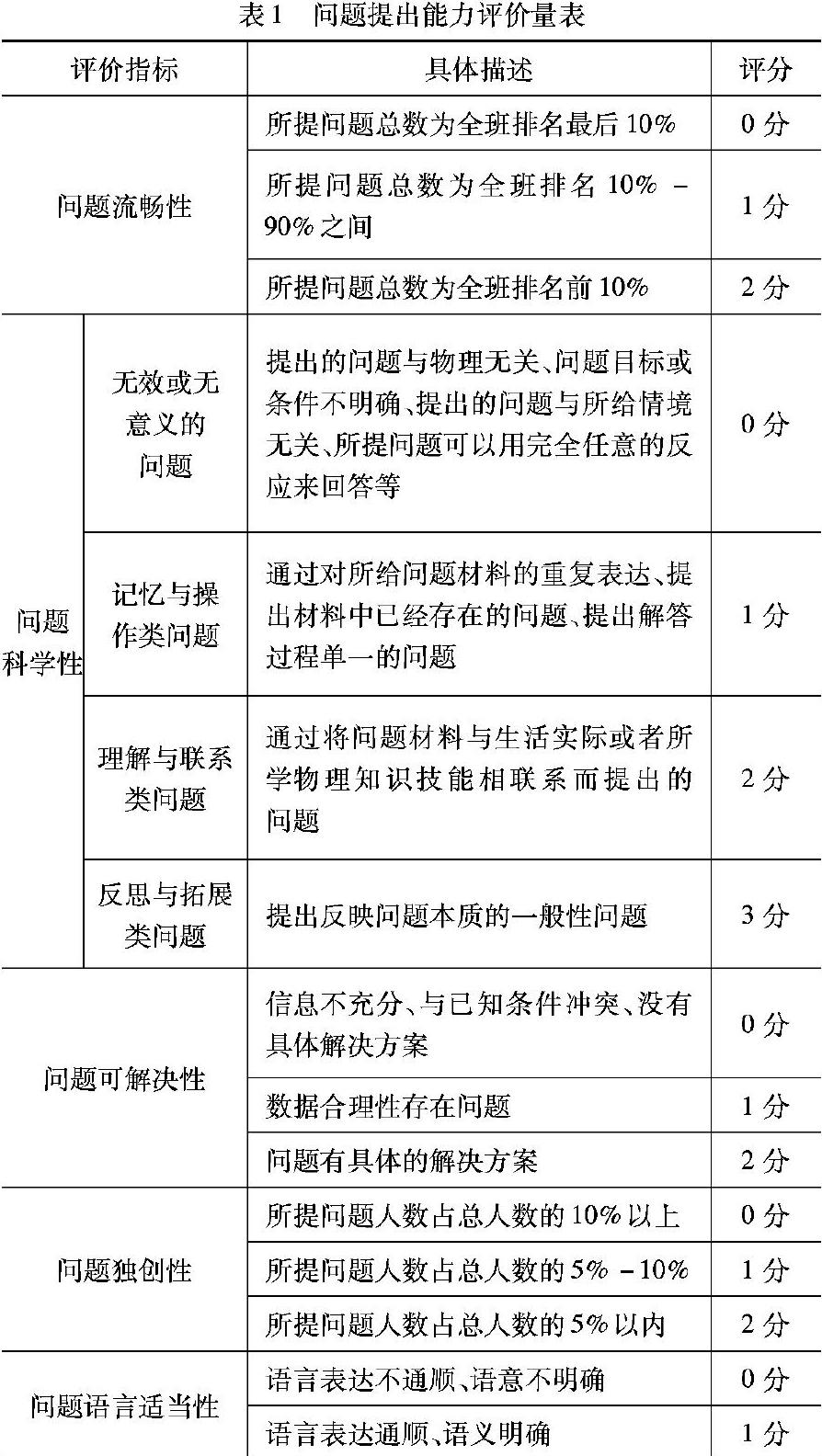
将问卷以及评价量表发给相关领域专家进行评价,根据专家意见进一步修正,并将问题提出能力测试卷发给几位大一新生,根据回收的问卷分析,对测试题以及评价量表进行修正,最终的评价量表见表1.
2 高中生问题提出能力的调查研究
2.1 调查研究过程
由于高中毕业生参加完高考后较为分散,所以选取大学开学后的大一新生作为研究对象.研究选取上海某双一流高校物理系的大一新生作为研究对象,研究对象均是接受过高中教育且高考包含物理这门学科的同学,第一次随机发放10份问卷,通过对回收的问卷进行分析,对评价量表的有效性和可信度进行初步验证,根据数据结果对问卷以及评价量表进行了进一步的修正.
将修正后的问卷随机发放110位大一新生,收回有效问卷100份,根据评价量表对学生的问题提出能力测试卷进行评分,并选取每个题目中得分最高的一个问题作为问卷的分数.
2.2 调查研究结果
2.2.1 高中毕业生问题提出能力现状
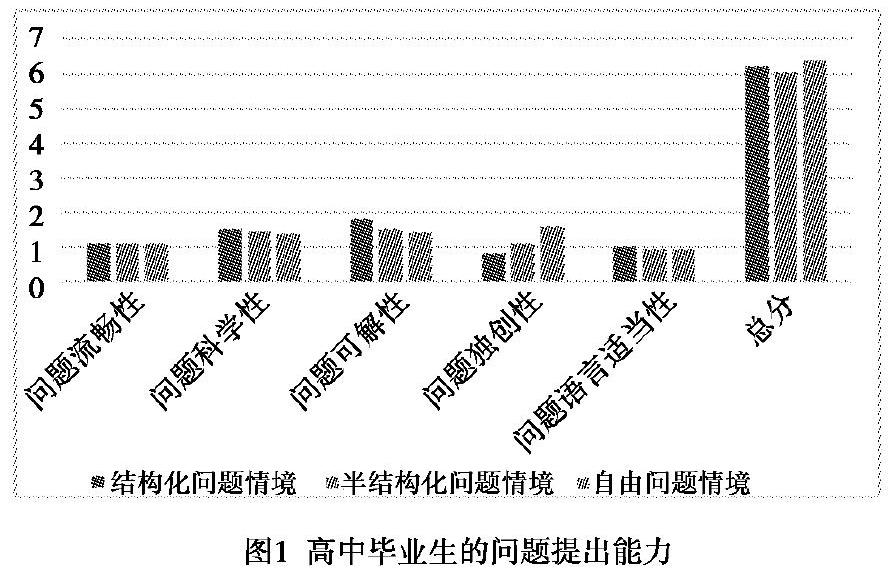
高中毕业生问题提出能力测试卷成绩的平均分如图1所示,调查结果显示,高中毕业生在三种类型的问题情境下提出问题的总分相差不大,但是具体的问题评价维度有一定的差异性.学生在结构化问题情境下提出的问题更具有可解性,在自由问题情境下提出的问题更具有独创性.
2.2.2 问题的流畅性
调查结果显示,高中毕业生在结构化问题情境和半结构化问题情境中提问的流畅性更高,而在自由情境下提问的流畅性较差.在结构化问题情境下学生提出的问题平均数量为4个,在半结构化问题情境下提出的问题数量平均为3.5个,而在自由情境下提出的问题数量平均只有2个.由此可见,学生在结构化以及半结构化问题中提问的流畅性明显高于自由情境.原因可能是问题情境给出的限制越少,学生要花费更多时间去补充问题情境,学生需要花费更多时间去回忆自己已经学过的相关知识或者做过的相关题目,进而选择自己要提出的问题所要达到的目的以及涉及到的知识内容,才能进一步提出问题,该过程相对于结构较为完整的问题情境需要花费更多时间,也要求学生有更加发散的思维能力以及更高的问题提出能力.
2.2.3 问题的科学性
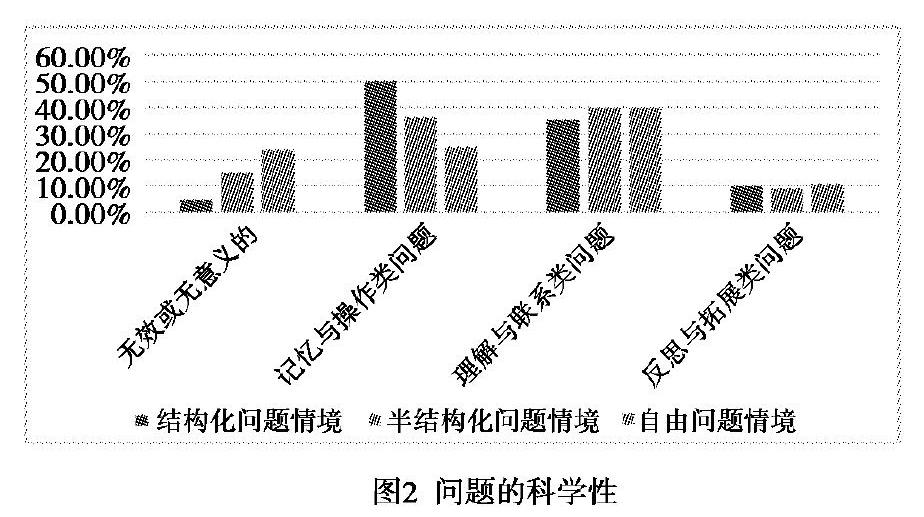
对三类题目中的问题类型进行统计,数据表明高中毕业生所提问题中属于理解与联系类型的问题最多,学生能够恰当地将问题情境与相关的物理知识联系起来形成新的问题,例如针对题目B1,有的学生提出问题:“若这一汽车在距离你s的地方开始刹车,汽车的初始速度为v0,以加速度a开始减速,当a满足什么条件时,这辆汽车才不会撞到你?”该问题中学生将匀减速运动与具体问题情境相结合,补充了必要的条件和所求项,形成了结构良好的问题,属于理解与联系层次.学生提出的记忆与操作类问题的数量也很多,例如针对题目A1,有学生提出了以下问题:“问题条件不变,小球上升到最高点需要多长时间?”该问题难度比原问题情境中的问题难度还要低,而且只需要运用一个公式v=gt即可解决,因此属于记忆与操作类问题.而学生提出的属于反思与拓展类型的问题更是非常少.由此可见,学生对基础教育阶段物理知识的理解相对扎实,但是很难达到对更高层次物理知识的理解和应用.
研究是对学生每道题目中得分最高的问题进行统计,但是对每道题目中学生所提问题的科学性进行统计,图2显示学生所提问题中很大一部分为无效或者无意义的问题,且学生在自由情境下提出的无效问题占比更多,例如,有的学生针对题目C1提出了如下的问题:“乙船在甲船下游,已知水流速度、初始相对距离、乙船速度,甲乙两船多长时间距离100m?”学生提出的这个问题中没有给出完整的条件信息,是无法对问题进行作答的,因此属于无效的问题.结构化问题情境中中学生提出的无效问题相对较少,可能是因为结构化问题情境中所给出的问题范例为结构良好问题,且提示学生只改变部分的问题条件来形成新问题,因此学生提出的问题大部分还是有效且有意义的问题,但是结构化问题中的记忆与操作类问题占比很高,学生更容易被给出的问题限制住思考,很容易提出对已有问题简单改编后的单一问题,这类问题往往不需要学生花费太多的时间,同时也无法促进学生对问题情境的深入挖掘和思考.
2.2.4 问题的可解决性、独创性以及语言适当性
高中毕业生在自由情境下提出的问题可解决性较差,更多的情况属于学生没有提供结构完整的问题.
高中毕业生在自由问题情境下提问的独创性更高,学生问题重复性很低,基本没有重复的问题,但是在结构化问题情境中学生所提问题的重复性很高,进一步说明学生在更加自由的问题情境下更能发挥自己的创造性.
大部分高中毕业生语言表述流畅且用词恰当.
3 结论
通过对部分高中毕业生的问题提出能力的调查,大部分学生还是缺乏问题提出的训练,所以应该在基础教育中融入问题提出的教学策略,首先可以从结构化问题情境开始对学生进行训练,学生在结构化问题情境下提问更加流畅,学生在提示下更容易提出问题,但是训练一段时间后应该给学生提供更多的半结构化或者自由情境,在自由情境下对学生提问的限制更少了,给了学生更多的思维发散空间,更有利于学生提出具有创造性的问题.
如何在基础教育中融入问题提出的教学策略,还需要进一步的探究,在此提出以下建议:教师首先要具备基本的问题提出能力,同时还应该具有问题提出的教学理念:要了解提问能力对学生的重要性,愿意在教学实践中培养学生的问题提出能力,还应该学习问题提出的教学策略,并积极地在教学中去运用,只有教师更多地关注学生的问题提出能力,学生才有机会在教育中受到问题提出的训练,而问题提出能力不是能够一蹴而就的,需要的是长时间的不断训练.
本研究的结论还存在以下的不足:在样本选取上可以更加广泛,研究选取的样本为上海某双一流高校大一新生,学生属于较高水平,因此得出的结论还不具备更广泛的适用性,后续研究可以对普通学校的大学生进行调查,还可以对比不同层次大学的学生问题提出能力的差异性.
参考文献:
[1]中华人民共和国教育部.普通高中物理课程标准(2017年版)[M].北京:人民教育出版社,2018.
[2]Stoyanova,E.,Ellerton,N.F.A framework for research into students problem posing in school mathematics[A]//P.C.Clarkson (Ed.).Technology in mathematics education[C].Melbourne,Australia: Mathematics Education Research Group of Australasia,1996:518-525.
[3]Xianwei Y,Van Harpen,Presmeg NC.An investigation of relationships between students' mathematical problem-posing abilities and their mathematical content knowledge[J].Educational studies in mathematics,2013,83(01):117-132.
[4]斯海霞.高中生數学问题提出能力发展进程研究[D].上海:华东师范大学,2014.
(收稿日期:2021-01-10)
