基于图像光散射颗粒粒度测量方法研究

曲佩玙，蒋 瑜，苏明旭，蔡小舒

(上海理工大学 颗粒与两相流测量技术研究所，上海市动力工程多相流动与传热重点实验室，上海 200093)

1 引 言

颗粒度测量技术在工业生产、食品、医疗以及环境保护等方面的应用十分广泛[1]。颗粒粒度分布对其特性有重要影响，如煤粉粒度对锅炉燃烧效率及电厂安全运行均与其分布相关[2]；乳液的微观结构、粒度大小和分布影响其稳定性和化学性能[3]；大气颗粒物的粒度分布，对保护生态环境和人类健康的研究将产生巨大影响[4]。

光散射式颗粒测量具有可测范围宽、精度高、可在线测量等优点[5]。基于Mie原理的静态光散射方法通过探测器检测前向小角度范围散射光能，分析颗粒粒度及其分布信息[6～8]。传统激光粒度仪以硅光电池或光电二极管阵列作为探测器，工作较稳定、技术较成熟，但应用中往往需人工或专用软件对中，操作繁琐且易受外界环境影响，分辨率也偏低[9]。

随着CCD图像传感器技术迅速发展，将其替代传统光电探测器具有可自动采集、可记录高分辨率的散射光信号的优势，结合图像处理技术可实现光环自动定中、动态分环，具有自动化水平高、测量精度高以及适应性较强等优点[10,11]，相关学者对此进行了研究。Oprisan A等[12]采用CCD相机对纳米胶体自由扩散过程中非平衡波动进行实验研究；Domínguez-García P等[13]利用CCD相机对磁流变液的三维形态进行表征；李彩荣等[14]采用CCD相机作为激光粒度仪探测器接收颗粒散射光能；Chen Q等[15]设计了基于线阵CCD探测器的前置式傅里叶透镜光学结构的实验装置系统，提出一种线阵CCD探测器的“动态”分环方式，但线阵CCD无法采集到整个焦平面的散射光信号。此外，以往大都采用对数划分形式确定CCD探测器环参数及颗粒粒级，合理的CCD探测器环数及颗粒粒级分配对散射光能矩阵性态乃至测量稳定性具有重要的影响。

本文结合图像处理与衍射散射法颗粒粒度测量技术，提出最小二乘原理圆拟合定环中心，优化CCD探测器光环参数与粒级划分的方法。搭建了测试系统，获取并验证各环散射光能信号，引入群智能差分进化算法反演颗粒粒度分布。通过标准颗粒对测量系统进行验证，并对2种水包油乳液进行了实测研究。

2 测量原理与系统

2.1 测量原理

根据Mie散射理论，初始光强为I0的激光通过各向同性的球形颗粒群时，在满足不相关单散射情况下，CCD探测器第n环上的光能可由颗粒群散射光强在该角度范围内积分：

(1)

式中：C′为常数；Wm为粒度Dm颗粒的频度分布，m为颗粒粒级分档数目；θn,1=arctan(rn,1/f)，θn,2=arctan(rn,2/f)，n为环数，rn,1和rn,2和 分别为CCD探测器第n环的内径和外径；f为傅里叶接收透镜焦距；i1、i2分别为垂直及平行于散射平面的散射强度函数分量(可通过Mie理论计算)，将积分式离散化：

(2)

式中：[E1E2…En]T为光能分布列向量，由CCD探测器实验测出；矩阵T为光能系数矩阵，元素Tn,m指直径为Dm的颗粒在第n环的散射光能，由探测器光环尺寸、入射光波长、接收透镜焦距、颗粒粒度以及颗粒相对折射率共同决定；[W1W2…Wm]T为将整个粒度分布划分为m粒级后各颗粒粒级分布，需通过反演计算求解。

2.2 测量系统

搭建的测量系统结构图如图1所示。功率为10 mW、波长为650 nm的半导体激光器发出激光束，经滤光片和0.01%×1%衰减片组合获得合适光强单色性好的初始入射光，再由扩束准直器(THORLABS，GBE03-A)和光阑形成直径10 mm左右的平行准直入射,光照射到样品池(含待测样液的石英比色皿)上，颗粒散射光信号包含其粒度分布信息，通过焦距75 mm傅里叶透镜汇聚于焦平面。用面阵CCD相机(THORLABS，DCU223M)以数字图像形式接收并传输至计算机。相机曝光时间可调，范围为0.1～60 ms；感光尺寸为1 024×768 pixels；接收镜头放大倍率为0.51倍；接收视场范围为9.33 mm×7 mm；经标定单个像元对应长度为9.3 μm。这些指标满足了分环条件的要求。

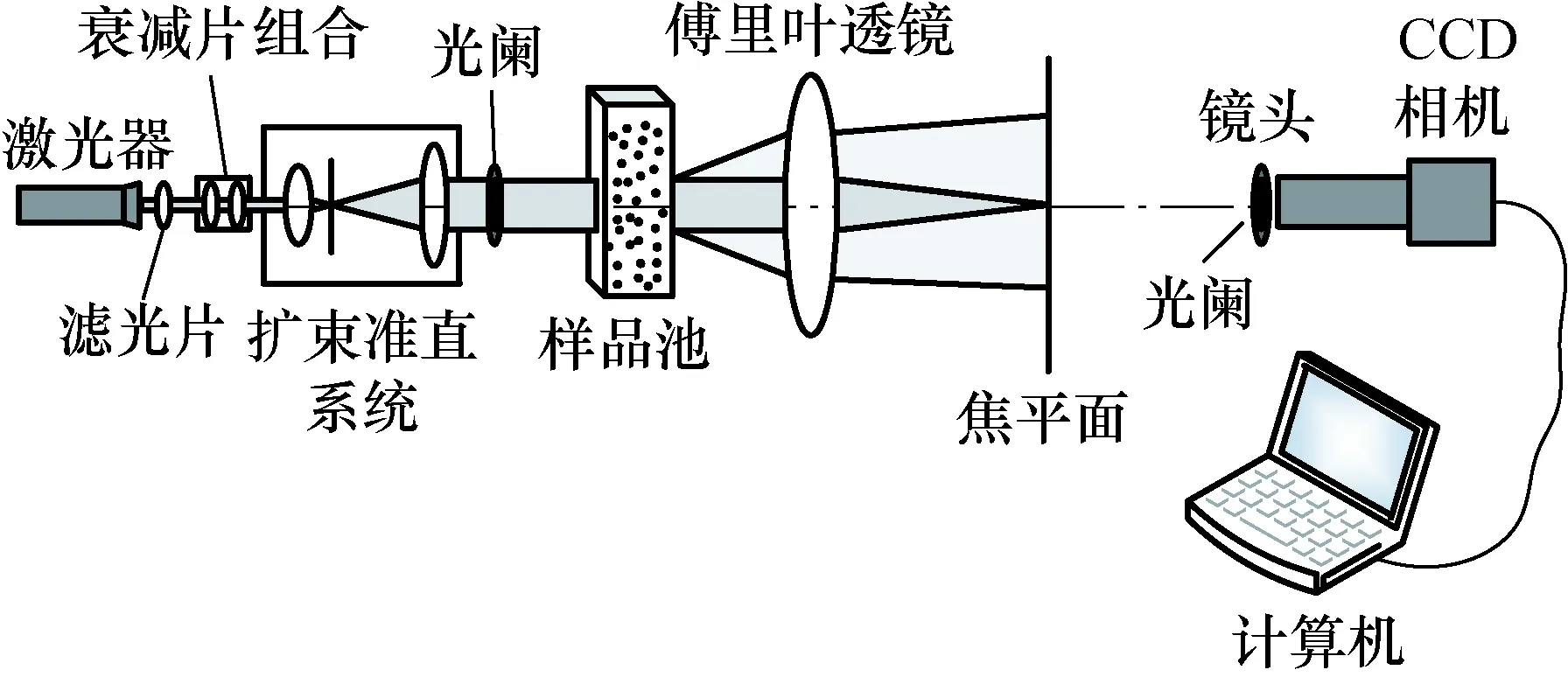
图1 测量系统结构图Fig.1 Structure diagram of measurement system

3 图像处理与光能提取

两类探测器散射光能示意图如图2所示。图2(a)所示为常规硅光电池或光电二极管阵列探测器，通常实验前需对中调试，操作繁琐，尤其不利于在线测量。图2(b)采用CCD相机采集散射光信号，散射光斑在感光元件上位置不敏感，可结合图像处理算法实现自动定中，合理动态分环，从而得到各环均匀分布的散射光能，合理利用散射光能。

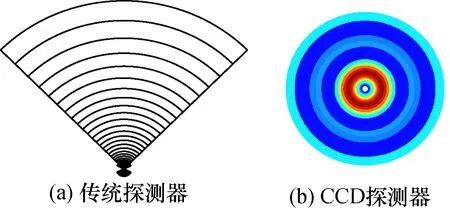
图2 两类探测器散射光能示意图Fig.2 Schematic diagram of scattered light energy of two types of detectors

3.1 最小二乘法确定中心过程

目前确定光环中心坐标主要有传统算法和重心法。传统算法以CCD感光元件横、纵向灰度值总和最大值交点为光环中心，实测过程常出现最大灰度值点多处相等的情况，而导致方法失效。重心法寻找二值化图像连通域几何中心，但对非理想圆斑，光斑形状会带来误差。鉴于采集颗粒散射实验信号时噪声和杂光影响图像信噪比，本文提出一种在图像预处理后，基于最小二乘法的光环中心坐标确定方法。检测预处理图像边界点并带入标准圆方程(x-A)2+(y-B)2=R2，令

(3)

可得：

(4)

式中：N为边界点个数；X、Y分别表示各边界点的横、纵坐标；圆心坐标(A,B)即为散射信号光环中心坐标。

图3给出标称直径57.9 μm的颗粒定中心过程。图3(a)为散射信号原始图像，可见较明显衍射光环；通过中值滤波滤除椒盐噪声，去噪后图像 3(b) 中散射信号更加均匀；图像二值化，把散斑从背景中分离，结果如图3(c)；通过开闭运算，填充散斑空洞、消除毛刺，结果如图3(d)；采用canny算子边缘检测，提取散斑轮廓信息如图3(e)；最后，边缘检测边界点作为最小二乘法拟合圆的输入像素点来确定出光环中心，结果如图3(f)所示。

图3 57.9 μm标准颗粒定中心过程Fig.3 Procedure of determining the center of rings for 57.9 μm standard reference materials

3.2 CCD光环尺寸设计

检测器光环尺寸设计对粒度测量至关重要，根据衍射极大值原理[16]，按公式(5)对CCD探测器环状尺寸进行设计。

(5)

式中：S(n)为CCD探测器感光元件圆环半径；d(m)为颗粒分档直径，一般可取光环数与颗粒粒级分档数一致(m=n)，即可计算并构造出光能系数矩阵T。

光环尺寸设计需综合两方面因素：测试分辨率和系数矩阵性态。通常分环数越多，则反演粒级区间和测量分辨率高，但复杂性也增大。T通常属于病态矩阵，采用对数分档方式，有利于改善矩阵性态，且在小角度范围内可获得更多探测区间，利于对大粒度颗粒的检测。本系统设计颗粒粒度测量范围为5～200 μm，所设计的光环尺寸范围为 0.105～4.212 mm。计算了30～50环系数矩阵条件数，35环对应条件数最小为1.04×1010，确定其为分环数。CCD探测器光环尺寸设计如图4所示，图4(a)为设计CCD光环尺寸；图4(b)为不同粒度颗粒(相对折射率m=1.596/1.33)在各环散射光能分布；图4(c)为分环和粒级数为35的系数矩阵三维图。

图4 CCD探测器光环尺寸设计Fig.4 Size design of ring for CCD detector

从图4可知，颗粒粒度增大，散射光能分布从探测器外环逐渐趋向内环。不同粒度颗粒散射光能分布差异性明显，利于5～200 μm颗粒粒度的分析。对应粒级系数矩阵的对角占优特性较好，且具有相对良态特性，有利于提高测量系统精确性与稳定性。

4 实验结果

选用北京海岸鸿蒙公司的聚苯乙烯乳胶球标准颗粒和大豆蛋白乳液为实验样品，表1为8种标准聚苯乙烯颗粒尺寸，颗粒单分散性好、粒度偏差小；两种大豆蛋白乳液由浓度为4%的大豆分离蛋白分散液，将油水占比分别为10%、40%的溶液混合高速剪切乳化形成Pickering乳液，该乳液颗粒呈球状形态。

表1 8种聚苯乙烯乳胶球标准颗粒尺寸Tab.1 Size of eight polystyrene latex particles

4.1 实验信号分析

将直径范围约10 μm～120 μm标准颗粒分别滴入装有去离子水比色皿，超声分散后制成待测样品，测试时控制光透过率范围在0.7～0.9之内，以保证单散射条件，CCD采集散射光信号如图5所示。根据设计CCD探测器光环区域划分，对各环像素点灰度值积分，提取出各环散射光能。

图5 标准颗粒实验信号图Fig.5 Experimental signal diagram of standard reference materials

图6为57.9 μm的标准颗粒样品采用两种算法定中后提取各环散射光能，与散射光能理论分布曲线对比可知，最小二乘拟合定中得光能与理论值分布更趋一致，二者间标准差仅为0.000 6。此外，采用个人电脑(Intel Core I5-5200U,内存4 GB)多次处理，重心法定中时间需要6～7 s，而最小二乘原理圆拟合仅需0.2～0.3 s，会更有利于数据快速处理。

图6 57.9μm标准颗粒散射光能分布Fig.6 Distribution of scattered light flux of 57.9 μm standard reference materials

4.2 粒度反演

颗粒粒度反演问题可归结为第一类Fredholm方程求解问题[17]。根据是否需事先假定颗粒粒度分布函数，又可分为非独立模式算法和独立模式算法。本文引入一种非独立模式差分进化算法(differential evolution,DE),DE算法是一种全局优化群体智能算法，具有很好的鲁棒性[18]。图7为DE算法流程图，其基本思想是：在解向量空间内对初始种群进行随机初始化，种群内两个随机个体差分向量经加权后与种群内相异个体相加产生新变异个体，其与非变异个体交叉产生试验向量，根据目标向量和试验向量的适应度值来确定最优个体并获最优解。图7中，t表示迭代次数。

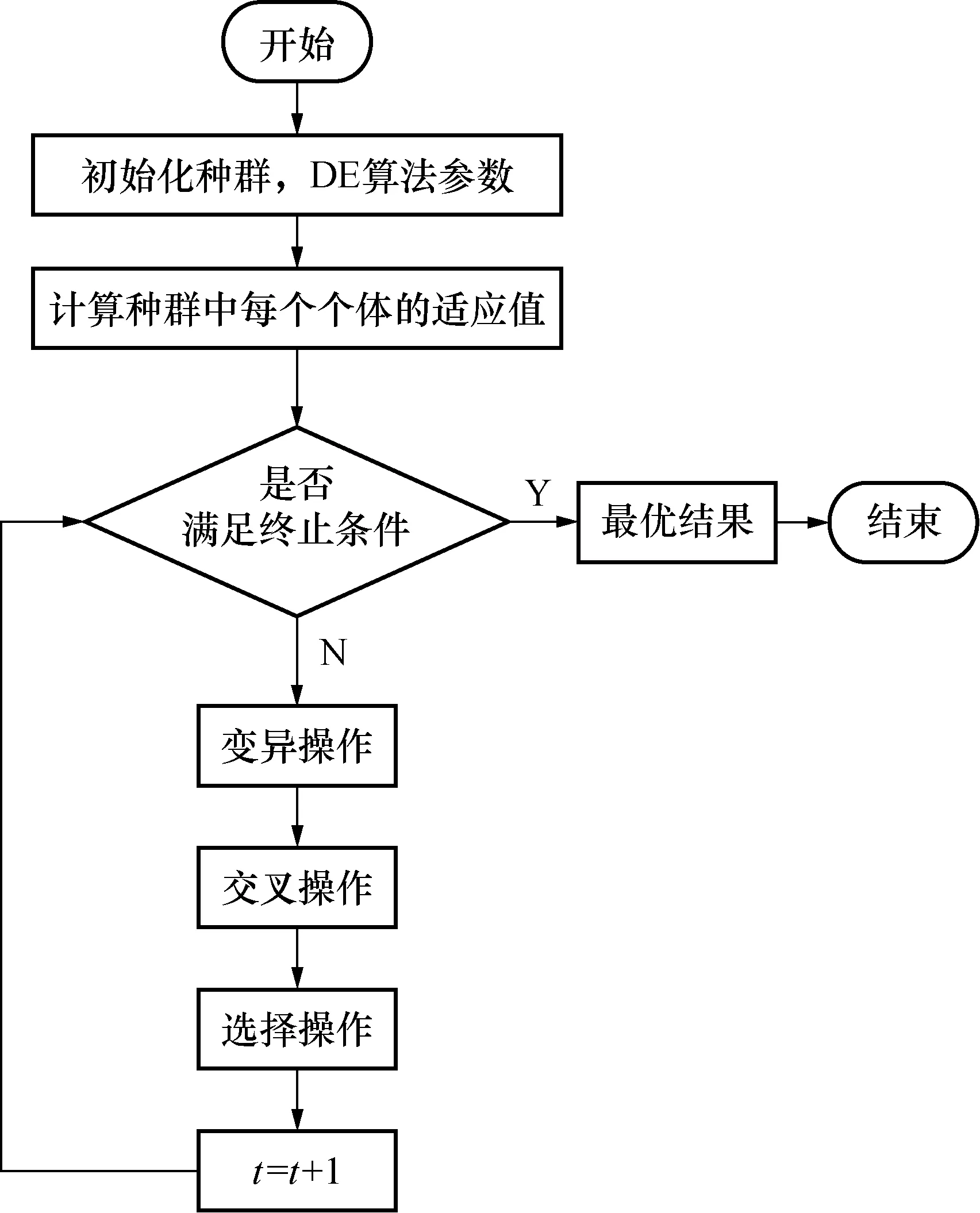
图7 DE算法流程图Fig.7 Flow chart of DE algorithm

对标准颗粒10次重复测量，将散射信号光能提取后反演出颗粒粒度，计算出平均粒度和标准偏差，结果如图8所示。以57.9 μm标准颗粒为例，按35环光环划分反演中位径Dv35=56.5 μm(与标称值误差小于3%)，优于常用31环中位径Dv31=54.1 μm。同时，其对于不同粒度颗粒分辨良好，与标称粒度数据的线性相关系数大于99.9%，各粒度35环情况下平均相对偏差1.3%，31环情况下平均相对偏差7.9%。

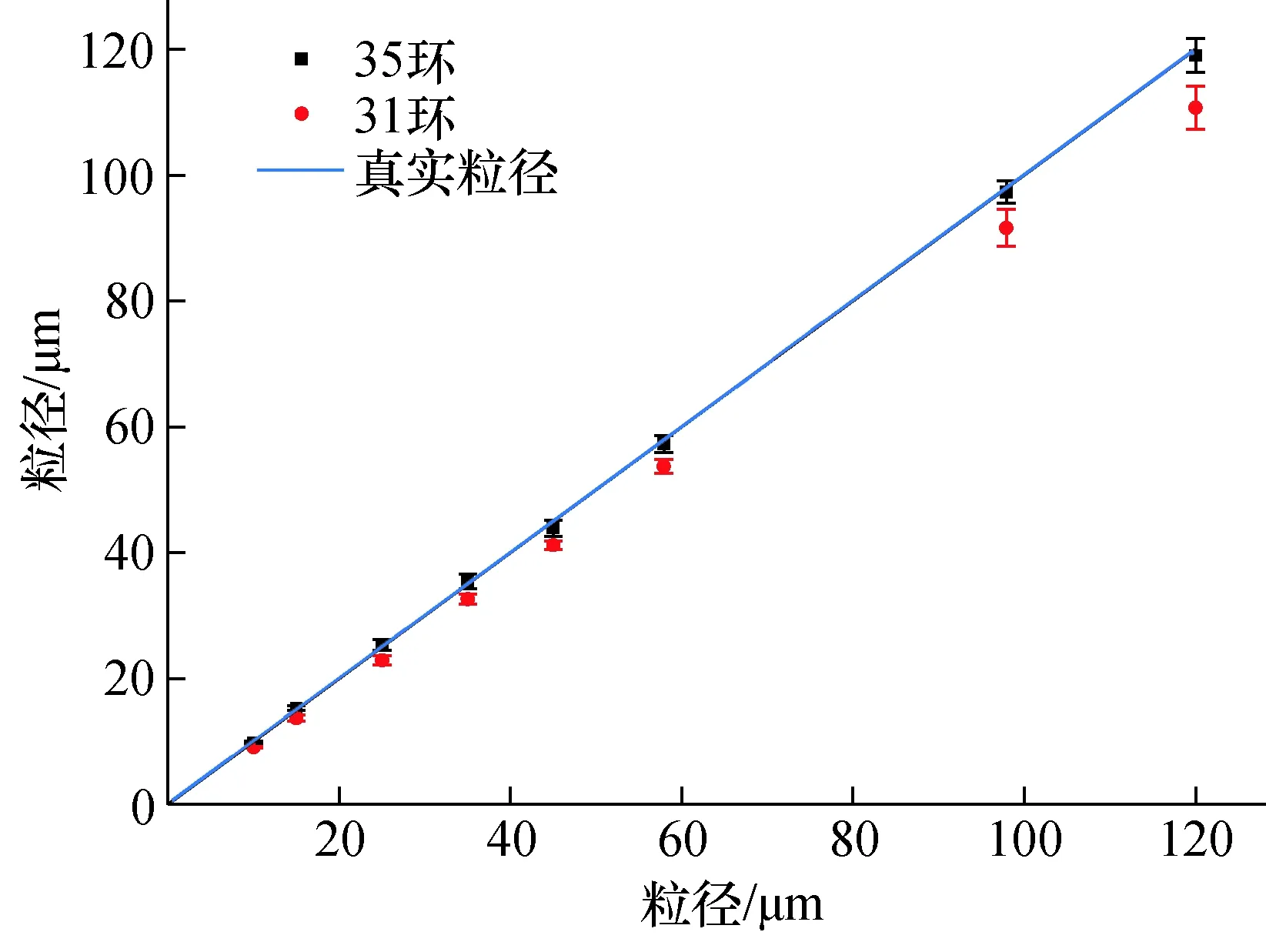
图8 标准颗粒测量结果Fig.8 Measurement results of standard particles

4.3 水包油乳液粒度测量

按照相同步骤，对体积分数为10%和40%(油水占比不同，乳化能力和粒度大小均不一样)的水包油乳液测量。待测水包油乳液以去离子水作为分散介质(相对折射率m=1.435/1.33)，稀释并用玻璃棒搅拌均匀后滴入比色皿进行测量，图9给出测量结果粒度分布。

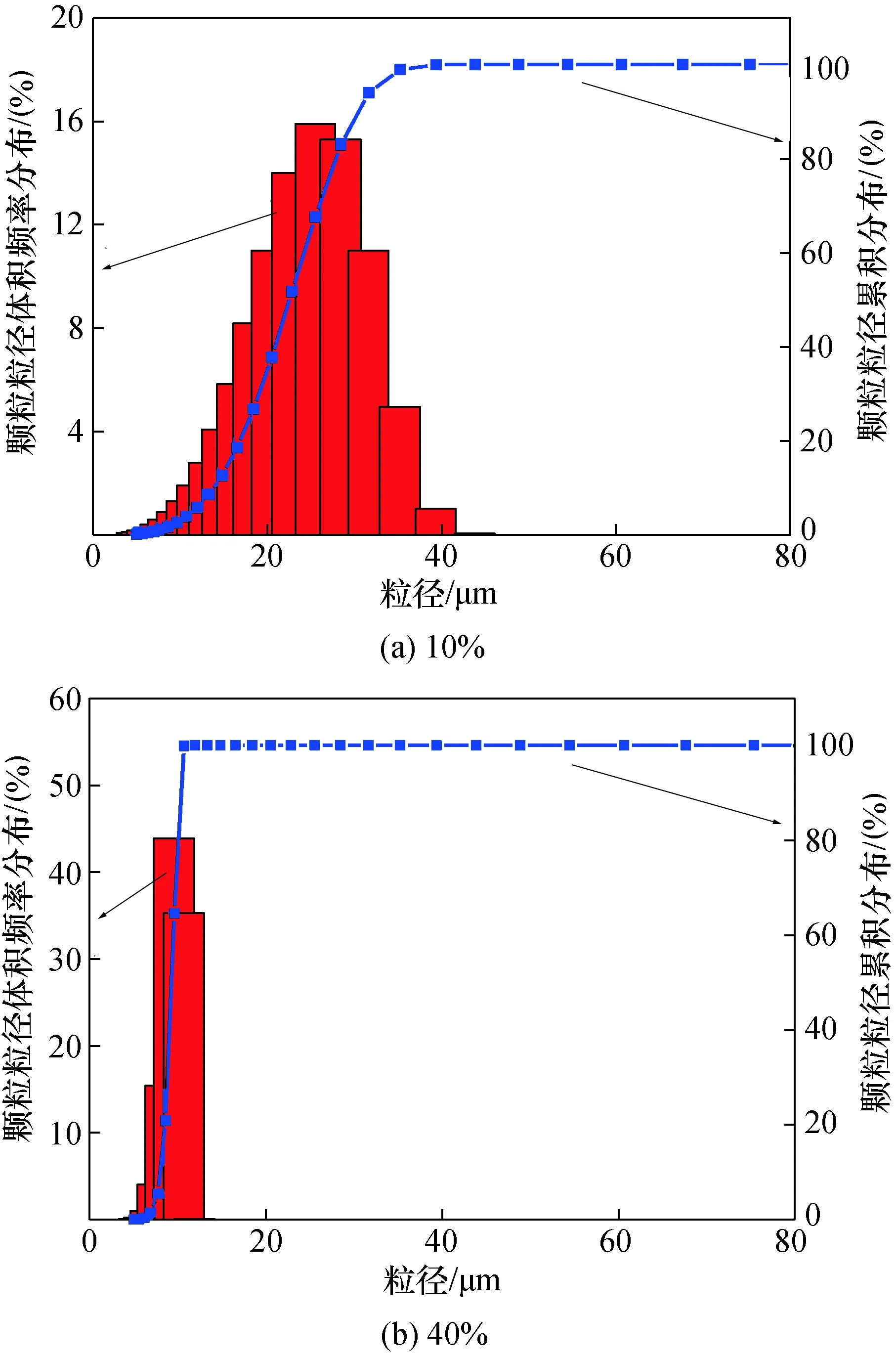
图9 不同油体积分数的大豆蛋白乳液粒度测量结果Fig.9 Particle Size Distribution of soy protein emulsion with different oil volume fractions

用PIP8.1型颗粒图像处理仪对两种乳液进行测量，仪器测试范围为0.5～3000 μm，重复性误差小于3%，常用于其它原理粒度仪的可靠性评判。对乳液测量时，用移液枪滴加约10 μm样品至载玻片上，用10倍物镜观察，由CCD相机拍摄经显微放大的颗粒图像，再由计算机内置软件分析颗粒粒度，通过更换视场，连续测试并累计颗粒数目至800以上，分析出颗粒粒度分布和体积平均粒径，测量结果见表2。

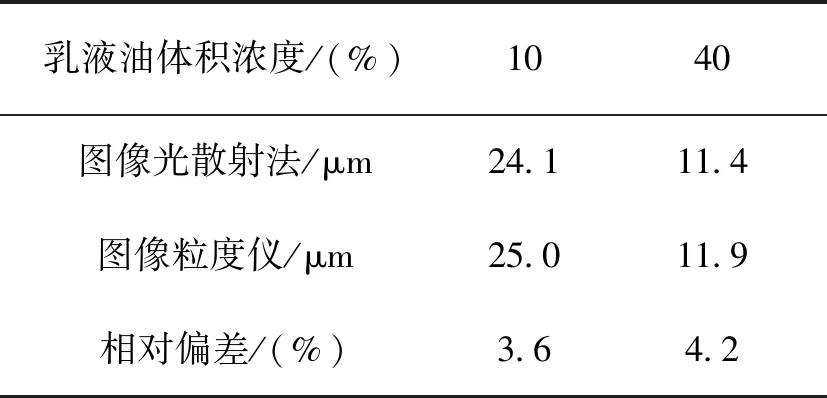
表2 大豆蛋白乳液测量结果对比Tab.2 Comparison of two measurement results of soybean protein emulsion

通过两种测量结果对比，可见基于图像的光散射颗粒粒度测量系统对水包油乳液测量偏差小于5%。

5 结 论

搭建了基于图像光散射颗粒粒度测量系统，采集到高信噪比的散射光图像。提出一种最小二乘原理圆拟合确定散射信号光环中心方法，设计了35环CCD探测器划分方式，计算出本系统参数下良态光能系数矩阵并采用DE算法反演标准颗粒粒度与标称粒度误差小于3%。实验结果表明：采用最小二乘原理圆拟合方法定中提取到的散射光能与理论分布更加吻合，35环的光环划分方式有利于获得相对良态特性的光能系数矩阵。本方法测得大豆蛋白乳液颗粒粒度分布与图像法对比误差小于5%，可为颗粒粒度测量提供一种光散射法有效改进方式。