基于深度信念网络的ECT图像重建算法

马 敏，孙 颖，范广永

(中国民航大学 电子信息与自动化学院，天津 300300)

1 引 言

电容层析成像(electrical capacitance tomography,ECT)以其非侵入式、无辐射性、低成本、响应快速等技术优势，作为一种多相流可视化的测量方法，受到国内外研究人员的广泛关注。它是以CT为基础而发展起来的一种层析成像技术，与CT技术所不同的是：ECT技术所处的领域为软场，所测量的信号分布与被测物质分布存在着复杂多变的非线性关系。

ECT图像重建的数学基础是奥地利数学家Randon的变换理论，具有典型的病态性、欠定性与非线性。1985年，Murai和Kagawa根据灵敏度定理，使用有限元方法对电导率分布图像进行了重建[1]。2005年，Soleimani等通过变分的方法重新推导出灵敏度定理，离散后的矩阵便是灵敏度矩阵[2]，灵敏度矩阵结合多种算法用于对反问题的求解。但通过灵敏度矩阵求解的过程中，会造成很大的误差，导致成像质量不佳。早在1994年，Nooralhaiyan等通过神经网络获得了将电容数据转换为油/气或油/水相分布的模型，开拓了神经网络应用在ECT技术中的道路。神经网络能够避免灵敏度的求解，于是越来越广泛地应用在ECT技术中。2014年，宋蕾[3]等提出Elman神经网络在ECT系统流型辨识中的应用；2018年，王莉莉等[4]提出自适应与附加动量BP神经网络的ECT流型辨识。

传统的神经网络具有浅层的网络结构，隐含层较少导致难以表征较为复杂的函数关系。被广泛应用于非线性系统中[5,6]的深度信念网络(deep belief network，DBN)，含有多隐含层，能够逐层地进行特征提取，对于复杂函数具有强大的学习能力。2017年，朱林奇等[7]提出融合深度信念网络与核极限学习机算法的核磁共振测井储层渗透率预测方法，构建了NMR测井横向弛豫时间谱与渗透率的非线性关系；2018年，刘梦溪等[8]研究了焊缝缺陷图像分类识别的深度信念网络。由于在ECT技术中,电容数据复杂多样且与介电常数呈非线性关系[9]，本文利用深度信念网络强大的学习能力，构建已检测电容值与图像灰度值的函数关系，简化图像重建的过程。为了提高重建图像质量、缩短DBN的训练时间，对该算法进行了改进。

2 ECT基本原理

2.1 ECT系统组成

本文所采用的ECT系统[10]主要是由三大部分组成：16电极电容传感器、数据采集系统以及图像重建系统。16电极电容传感器是用来测量极板间的电容数值；数据采集系统是将传感器测量的数据进行收集、滤波、变换等处理，并将数据传送给图像重建系统；图像重建系统将得到的数据通过软件与图像重建算法进行图像重建，最终得到重建图像呈现在PC机上。ECT系统结构如图1所示。

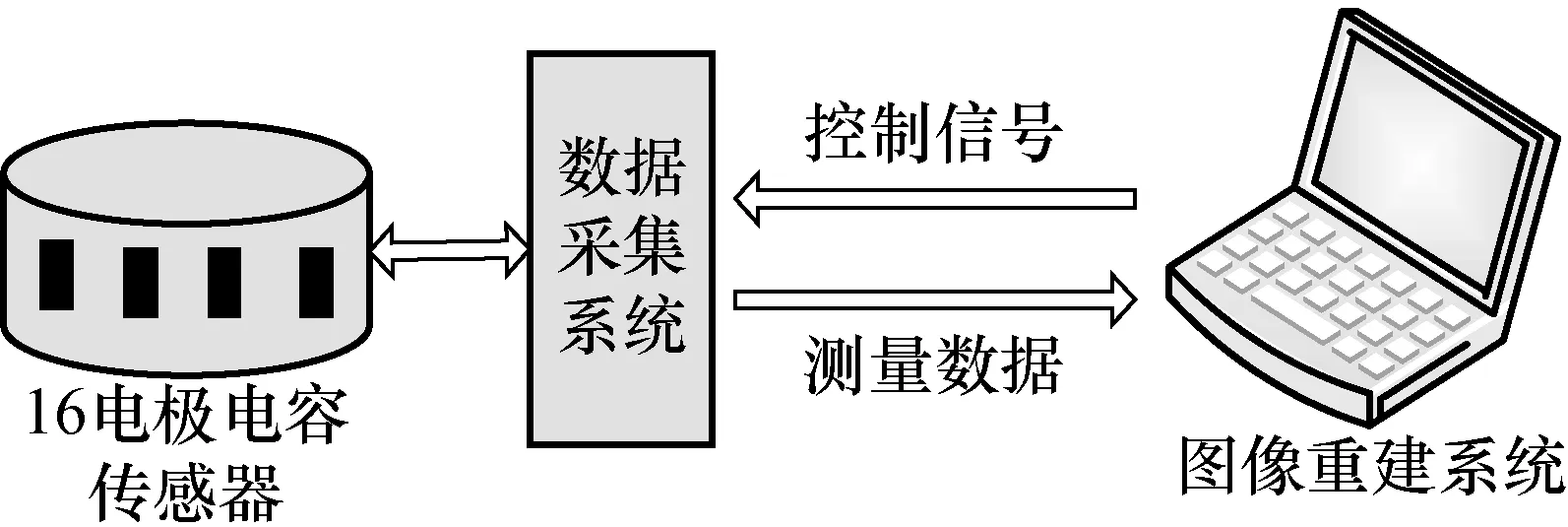
图1 ECT系统结构图Fig.1 System structure diagram of ECT

2.2 ECT成像原理

在ECT系统中主要涉及到的数学问题就是正问题[11]与反问题[12]。ECT中的正问题可归结为：已知传感器结构、激励/测量模式、介电常数分布等条件，求解场域内极板间的电容值、电荷量等数据值，最终得到灵敏度矩阵。反问题是相对于正问题而言，根据正问题中得到的灵敏度矩阵，反演介质在场中的分布，图像重建就是求解反问题的过程。

将电容值与介电常数分布的非线性关系离散归一化[13]，得到近似线性的逆问题模型[14,15]为：

C=S×G

(1)

式中：C∈Rm×1;S∈Rm×n;G∈Rn×1;C为电容值;S为灵敏度矩阵;G为介电常数;m为电极的对数；n为剖分的网格数目。

电容层析成像的最终目的是求解得到介电常数G。为得到介电常数G的值，将DBN引入到电容层析成像技术中，只考虑电容值C与介电常数G，不需要再对灵敏度矩阵S进行求解；而是利用DBN构建电容值与介电常数分布的非线性关系，输入已检测的电容值C，直接得到介电常数分布的图像灰度值。

2.3 电容值的求解

假设ECT场域内不存在自由电荷，ECT敏感场的数学模型可表示为：

[ε(x,y)φ(x,y)]=0

(2)

式中：ε为介电常数在管道内的分布函数;φ为场域内电势分布函数。

进而得到:

ε(x,y)φ(x,y)+ε(x,y)2φ(x,y)=0

(3)

利用高斯定律，得到电极上的感应电荷Qij为：

(4)

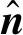
(5)

通过传感器系统测得独立值电容值的个数由式(6)表示，本文选取16(n=16)电极，所以会得到120个电容值。

(6)

3 深度信念网络

深度信念网络(DBN)是多个RBM[16]模型堆叠而成的能量概率分布模型，训练过程分为预训练和微调两个阶段。在预训练阶段，采用对比散度(CD)算法对每个RBM进行逐层无监督训练，初始化网络参数，其中RBM的输出层(隐藏层)将会作为下层RBM的输入层，每一层RBM的训练结果是对输入数据的非线性变换，以此类推，逐层完成RBM的预训练。微调阶段，可根据性能、需求采用不同的算法，利用误差反向传播优化参数空间。

3.1 受限玻尔兹曼机

RBM是一个两层的无向图模型，包含一个可见层V和一个隐藏层H[17]，结构如图2所示。可见层和隐藏层的神经元在层内无连接，层间全连接。可见层用于接收输入数据，隐藏层是对可见层进行重构，可视为特征提取层。

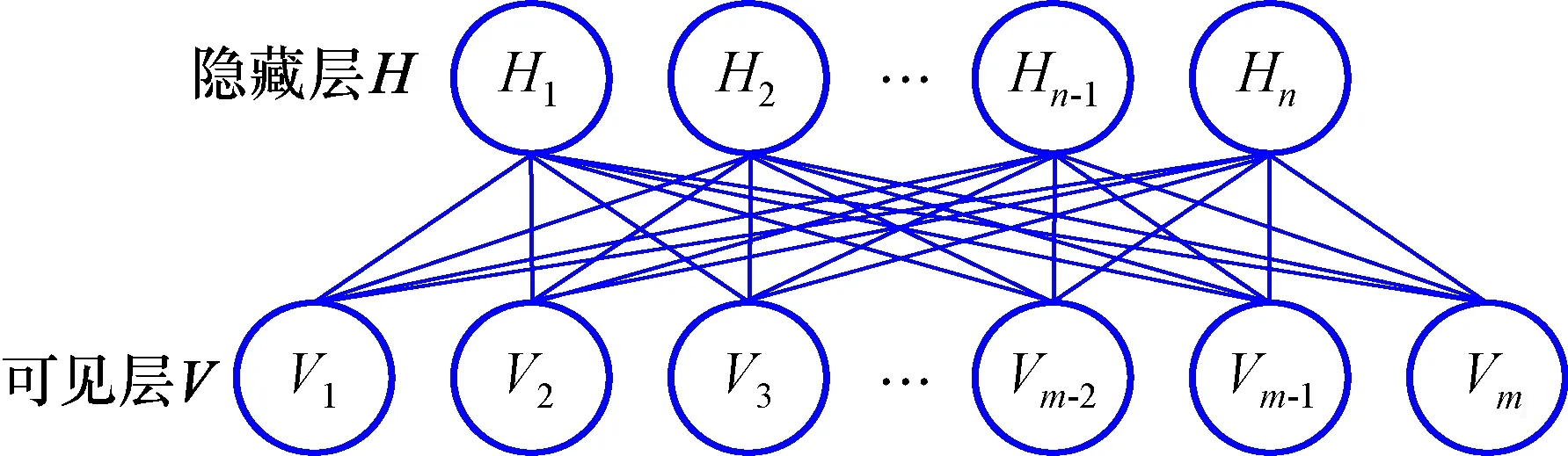
图2 RBM结构图Fig.2 Structure Diagram of RBM

假设所有的隐藏层单元h和可见层单元v均为二值分布，即∀i,j，vi∈{0,1}，hj∈{0,1}。对于给定的一组状态(v,h)，RBM的能量函数为:

(7)

式中：m为可见层单元数目；n为隐藏层的单元数目；θ={wij,ai,bj}是RBM的参数；wij是隐藏层单元与可见层单元之间的连接权重；ai和bj分别表示可见层和隐藏层单元的偏置。根据能量函数，可以得出这组状态(v,h)的联合概率分布为:

(8)

(9)

Zθ为归一化因子。根据RBM的结构性质可知，在给定可见层单元v(或隐藏层h)的基础上，各个隐藏层单元h(或可见层单元v)的状态是相互独立的，因此计算出第j个隐藏层单元和第i个可见层单元的条件概率分布分别为:

(10)

(11)

其中

(12)

当给定1组训练样本集合S={v1,v2,…,vn}时，其目标就是最大化如下似然函数:

(13)

式中N表示训练样本数量。为寻求最优参数θ，采用梯度上升法求Lθ,S的最大值。参数θ的更新公式为:

(14)

式中η表示步长。假设只有一个训练样本，则对数似然函数Lθ对参数θ中wij、ai和bj的偏导数分别为:

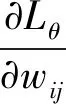
(15)

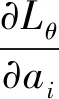
(16)

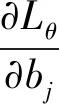
(17)

[·]data和[·]model分别表示Pθ(h|v)和Pθ(v,h)两个概率分布的数学期望，由于在实际计算中[·]model很难得到，因此利用CD算法中的k步Gibbs采样方法得到其近似值[18]，其近似值表示为[·]k。

3.2 深度信念网络的构建

对于DBN的构建，首先要确定输入数据电容值与输出数据图像灰度值。确定输入输出数据后，对于隐藏层数进行确定。为了选取较为准确的隐藏层[19]，逐渐对隐藏层的个数进行增加，最多增加到10层，得到了不同层数的错误率[20]，如图3所示。

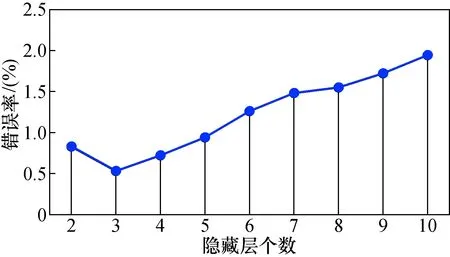
图3 不同层数的错误率Fig.3 Error rate of different layers

可以发现当隐藏层为3时效果最好，因此本文构建具有3层RBM的DBN。每个隐藏层的节点数根据经验设置，DBN隐含层的节点数分别为100-50-300。数据集中的训练数据均用来初始化3层网络的参数空间。

使用BP网络进行反向微调，对深层网络进一步优化，数据集中的训练数据均用来优化、更新参数空间。利用构建好的DBN网络，对存储的数据进行预训练与反向微调。DBN模型结构如图4所示。

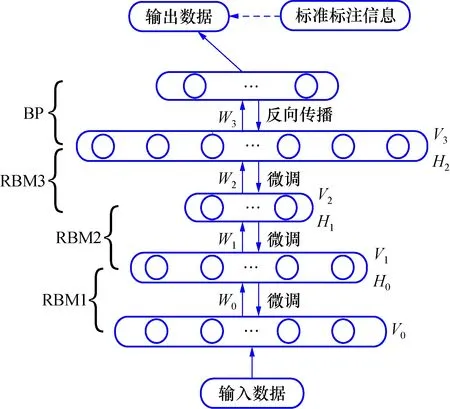
图4 DBN模型结构图Fig.4 Structure Diagram of DBN Model

3.3 深度信念网络的改进

(1)引入自适应步长的预训练过程

由于在CD算法中每个RBM均需要进行多次迭代，且每次迭代后的参数更新方向不尽相同，所以需要选择适当的步长η。如果选择的η较大，容易引起振荡；如果η较小，则会导致收敛速度缓慢。为解决这个问题，采用了一种自适应步长(adaptive step,AS)的方法[21]。

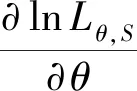
(18)

式中：α>1表示η的增加系数，β<1表示η的减小系数，且0<β<α。如果2次连续的参数更新方向相同，则η增加；如果方向相反，则η减小。引入自适应步长后参数更新机制发生了变化，参数wij、ai和bj的更新公式分别为:

wij=wij+η*([vihj]data-[vihj]k)

(19)

ai=ai+η*([vi]data-[vi]k)

(20)

bj=bj+η*([hj]data-[hj]k)

(21)

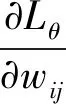
(2)基于BFGS拟牛顿法的微调过程

在DBN微调过程中，一般利用BP算法进行有监督地参数微调，基于最速下降法沿目标函数的负梯度方向调整参数。但是这种方法在越接近目标值时，收敛速度越慢，从而导致训练耗时长的问题。因此本文采用BFGS拟牛顿法[22]替代最速下降法来加快学习速度。

BFGS拟牛顿法是对牛顿法的改进，利用目标函数值和一阶导数的信息构造出近似的Hessian矩阵，解决了牛顿法需要计算Hessian矩阵而导致工作量大的缺陷，同时保留了牛顿法收敛速度快的优点。

在BFGS拟牛顿法中，目标函数F的定义如下：

(22)

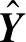
γk+1=γk+αkdk

(23)

式中：dk表示第k步迭代的搜索方向；αk表示第k步搜索方向的步长，一般沿搜索方向做一维搜索获得最优步长。

(24)

设目标函数F的梯度为g，即:

g=F(γ)

(25)

令第k步迭代的搜索方向dk为:

(26)

其中Bk为近似Hessian矩阵。

(27)

其中,

sk=γk+1-γk

(28)

yk=gk+1-gk

(29)

因此，在预训练阶段引入自适应步长(AS)，解决固定步长难以寻找全局最优的问题；在微调阶段采用BFGS拟牛顿法加快网络学习速度，减少训练时间。具体的算法流程如图5所示。

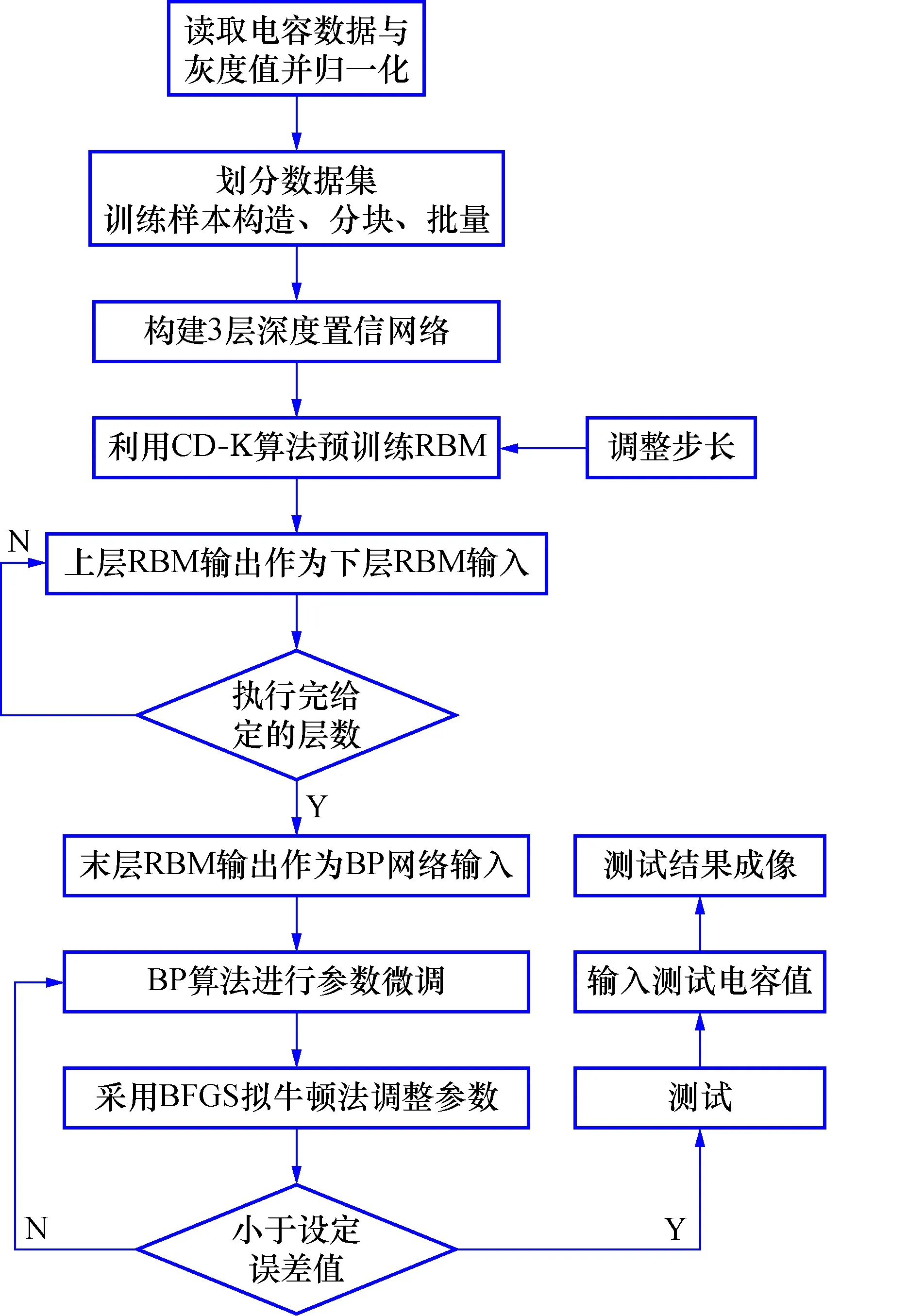
图5 算法流程图Fig.5 Diagram of algorithm flow

4 实验与分析

4.1 仿真设计

在本文的仿真实验中，通过COMSOL5.3软件对16电极ECT传感器系统进行建模，对传感器系统进行有限元分割，分割网络设置为64×64，剖分单元为三角单元，通过有效网络来求解场内的电容值。主要对核心流、双泡流、三泡流、层流以及环状流进行了仿真设计，建立模型如图6所示。其中电极板、屏蔽罩和极板的介电常数设置为2.2，管道的介电常数设置为5.8，空场材料的介电常数设置为1，被测物质流型设置为4.2。

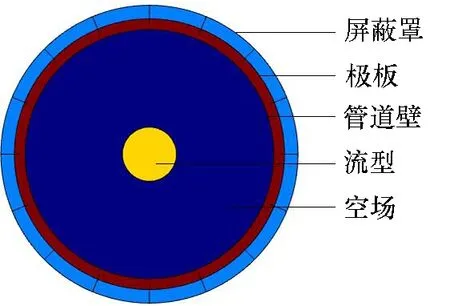
图6 传感器系统仿真图Fig.6 Simulation Diagram of Sensor system

通过MATLAB2014a进行编程，将原流型的图像分成3228个网格，分别代表了3228个介电常数值。对于流型与空场的介电常数设置一定的阈值，小于1.5的介电常数统一设置为灰度值255，大于3.5的介电常数统一设置为灰度值0，其余的介电常数值映射到灰色的灰度值范围。得到的灰度图像如图7所示。

图7 原流型灰度图像Fig.7 Gray-scale image of the original flow pattern

由于使用的是16电极的电容传感器，采样得到120个独立电容值，120维的数据将作为DBN的输入。同时使用MATLAB2014a，将原流型图分成3228个网格，意味着有3228个数据，DBN的输出是3228维的数据。通过仿真设计共获取训练数据7500组，其中每种流型数据为1500组。

4.2 图像重建

运行MATLAB2014a软件，通过常用的算法(LBP、Landweber)对已建模型进行图像重建。再通过DBN与改进DBN对存储数据进行训练与反向微调，使用测试数据进行成像；把得到的图像与传统算法的图像进行对比。为了体现对比效果，将传统算法的重建图像也设置一定的阈值，转变成灰度图像。各流型的图像重建结果如图8所示。

图8 各流型重建图像Fig.8 Reconstruction images of various flow patterns

4.3 实验分析

本次实验仿真利用重建图像的图像相关系数(CORR)与图像误差(IME)对图像效果进行分析。图像误差越小，图像相关系数越大，说明重建图像的效果越好。图像误差IME和图像相关系数CORR的计算公式如式(30)、(31)所示：

(30)

(31)

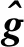
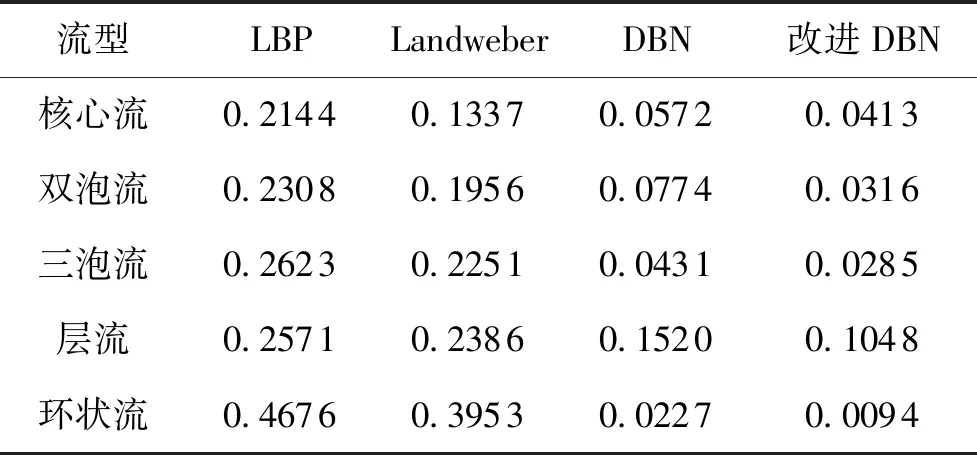
表1 IME的计算值Tab.1 Calculated values for IME

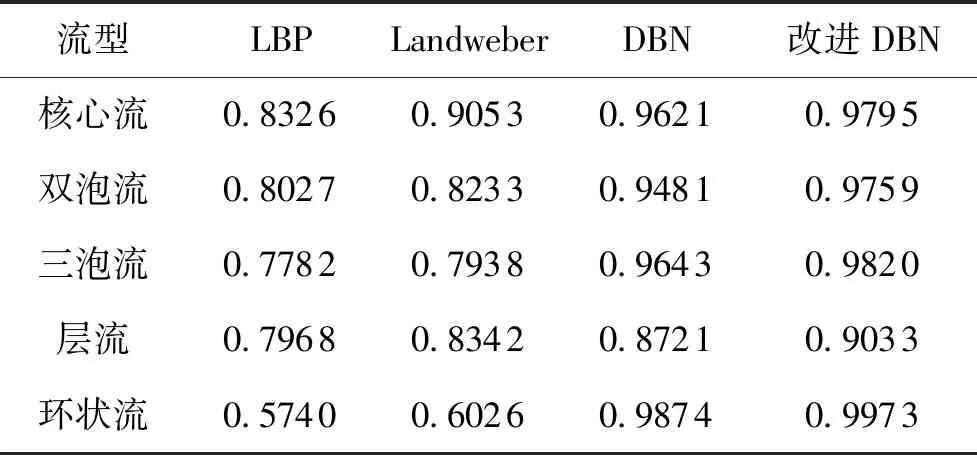
表2 CORR的计算值Tab.2 Calculated values for CORR

由CORR与IME的数据可以看出，通过DBN重建的图像明显优于传统算法的重建图像，改进DBN的重建效果比DBN的重建效果也有了提高。

对环状流，LBP与landweber重建误差最大，而通过DBN与改进DBN重建误差最小；改进DBN的图像误差低至0.009 4，相关系数高达0.997 3，说明DBN对环状流的重建有显著效果，为更好地重建环状流提供了基础。

在改进DBN中，微调阶段采用BFGS拟牛顿法加快网络学习速度，减少训练时间。通过实验得知采用DBN进行数据训练的时间为21.25 s，而改进DBN将训练时间缩短到15.74 s，说明改进DBN不仅改善了重建效果，还缩短了训练时间。虽然DBN的训练时间较长，但对于已经训练好的数据进行图像重建时，能达到图像重建的实时性，明显要优于传统算法。

5 结 语

本文将DBN应用在电容层析成像技术中，良好的重建效果验证了DBN应用在ECT技术中的有效性和可行性。从预训练和微调两个阶段对传统DBN进行了改进，在预训练阶段引入自适应步长(AS)，避免了固定步长所造成的难以寻找全局最优的问题，提高了重建图像质量；在微调阶段，采用BFGS拟牛顿法替代最速下降法，加快了网络学习速度。当确定了DBN的最优深度，对于训练数据规模也有很大的要求时，若训练数据规模不足，DBN则会出现过拟合现象。因此为了使DBN在电容层析成像技术可以得到更广泛、更有效的应用，对于训练数据规模不足的情况，还有待进一步研究。