结合粒子滤波及度量学习的目标跟踪方法

王洪雁，张莉彬，陈国强，汪祖民，管志远

（1.浙江理工大学信息学院，浙江 杭州 310018；2.大连大学信息工程学院，辽宁 大连 116622；3.五邑大学智能制造学部，广东 江门 529020；4.河南大学计算机与信息工程学院，河南 开封 475004；5.杭州电子科技大学电子信息学院，浙江 杭州 310018）

1 引言

作为计算机视觉领域的研究热点，视觉跟踪基于可见光等媒介持续感知目标，在视频监控[1]、自动驾驶[2]、人机交互[3]等方面具有广泛应用。近年来，众多高效且稳健的视觉跟踪算法相继被提出[4]，极大地促进了视觉跟踪的工程化进程。然而，由于实际场景的复杂性，跟踪过程中存在诸如光照变化、目标遮挡等不确定因素，从而导致跟踪性能显著下降[5]。因此，如何提高复杂场景下目标跟踪算法精度及稳健性仍是视觉跟踪领域的研究难点之一[6-7]。

针对复杂场景下视觉跟踪性能下降问题，文献[8]提出深度学习跟踪（DLT,deep learning tracking）算法，其基于堆叠降噪自编码器无监督训练以获得目标特征，且解码器后接分类层以区分目标背景进而实现目标跟踪。然而，由于自编码器仅可提取浅层特征，表达能力有限，因而目标跟踪实时性较差。针对此问题，基于卷积神经网络（CNN,convolutional neural network）高效且稳健提取目标特征的特点，文献[9]首先分析CNN 各层输出特征，而后构建特征筛选网络以实现匹配跟踪。需要注意的是，匹配方法虽具有较好追踪性能，然而由于跟踪前需基于巨量数据预训练所构建网络以学习通用特征表示，从而导致计算复杂度显著上升、数据过拟合等问题。为解决此问题，文献[10]提出基于卷积网络的跟踪器（CNT,convolutional network based tracker），其基于轻型两层卷积神经网络以降低计算复杂度，且此网络不需要大量训练数据即可提取较稳健的目标特征。然而，此方法所提模板更新策略涉及的参数值需基于经验确定，因而跟踪性能提升有限。基于此，文献[11]融合深度卷积网络良好的特征提取特性及复杂场景下粒子滤波优异的跟踪能力，以提升遮挡及噪声等条件下跟踪性能，并利用简单的在线更新策略抑制跟踪器漂移，同时对目标形变更稳健。值得注意的是，上述跟踪系统基于欧氏距离度量模板与候选目标之间的相似性，然而帧间目标外形变化通常较明显，从而导致欧氏距离无法精准度量目标特征分布，进而使目标跟踪性能改善有限。针对此问题，文献[12]提出基于深度度量学习（DML,deep metric learning）的跟踪模型，其基于前馈神经网络学习分层非线性距离度量，以提升模板与候选目标之间的度量精度。然而，该模型需基于大量数据训练非线性度量网络，因而计算复杂度较高，且样本有限场景下所得非线性度量网络度量精度较差，从而使跟踪精度改善有限。

针对上述问题，本文提出基于粒子滤波与核回归度量学习（MLKR,metric learning for kernel regression）的跟踪方法以提高目标背景的可分性。所提方法首先离线训练CNN，以提升网络特征提取及泛化能力，并基于训练所得CNN 获取目标高层特征；其次，利用核回归度量学习优良的正负样本区分能力[13]，对目标背景样本构建MLKR，以获取表征最优候选目标的度量矩阵并构造目标观测模型；最后，基于短时与长期稳定更新结合的更新策略在线更新模板，以降低遮挡、形变等不利因素影响，从而实现基于粒子滤波框架的有效跟踪。仿真表明，与现有主流方法相比，复杂场景下所提方法具有较高跟踪精度及较好稳健性。

2 所提目标跟踪方法

所提方法整体框架如图1 所示，其主要由如下部分构成：基于给定运动目标测试序列以离线训练CNN；基于MLKR 学习加权距离度量以最小化核回归预测误差从而实现动目标精确定位；基于短时更新与长期稳定更新联合更新策略以改善跟踪精度及稳健性；基于CNN 所提取深度特征以及粒子滤波框架实现目标跟踪。

2.1 度量学习模型

相较于仅度量各特性差异的欧氏距离，马氏距离可更有效地计算未知样本间的相似度，且可表征各特性之间的关联[14]。因此，为了更有效地区分正负样本，本文基于样本间马氏距离可学习的核回归方法获得最优映射矩阵A，而后最小化核回归预测误差以精确估计目标位置，进而提升跟踪性能。

基于训练样本集x=(x1,x2,…,xn)∈RB×N核回归度量学习，可以将训练样本数据映射至高可分性空间，从而获取表征目标特征差异的距离度量，即

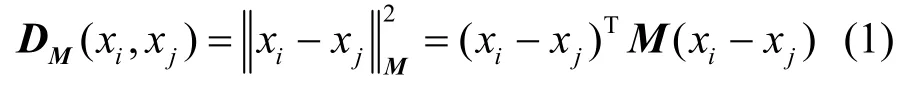
其中，B、N分别为样本特征维度、数量，DM(xi,xj)为xi和xj之间的马氏距离，为样本间距离平方，M为度量矩阵，具有半正定性[12]。由于直接学习M需要明确半正定约束，因此计算效率较低[13]。为降低计算复杂度，可对其实施Cholesky 分解，即M=ATA，A∈Rb×B可视为从原空间RB到新度量空间Rb的映射矩阵，其中b≪B，则可得

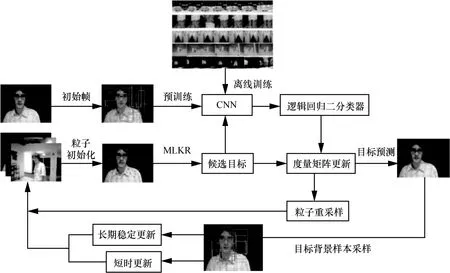
图1 所提方法整体框架

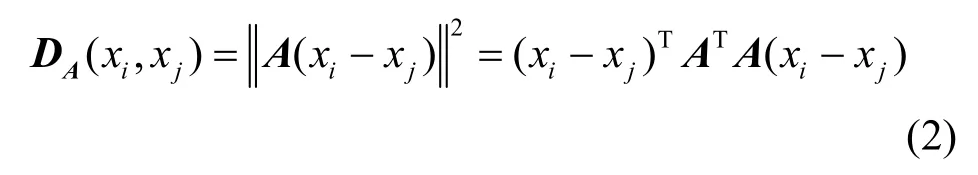
核回归中样本xi的目标估计值可通过邻近样本加权平均获得，如式(13)所示[15-16]。

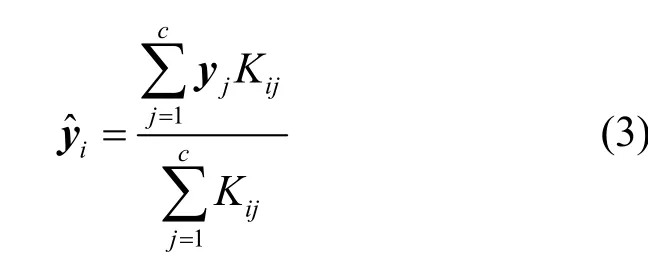
其中，c为xi的邻近数，y=(y1,y2,…,yn) ∈{0,1}为x对应类别标签，Kij为xi与邻近样本xj之间高斯核距离函数，表征二者之间相似性，可表示为

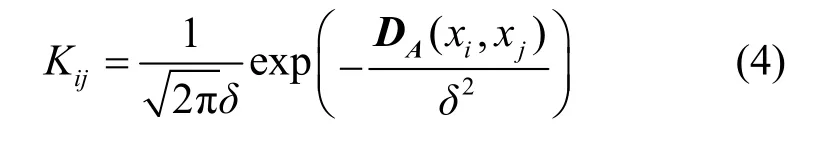
其中，δ为正则化参数，仿真实验中设置δ2=1。

本文采用累积二次回归误差表征训练样本误差L，并最小化此误差以获得最优映射矩阵A，即

不难发现，式(5)为关于变量A的非线性问题，较难直接获得闭式解。相较于其他方法，梯度下降法仅需估计一阶导数，计算复杂度较小、优化结果较好[13]。因此，本节基于梯度下降法求解此问题。基于链式法则，式(5)中目标函数关于变量A的导数可表示为

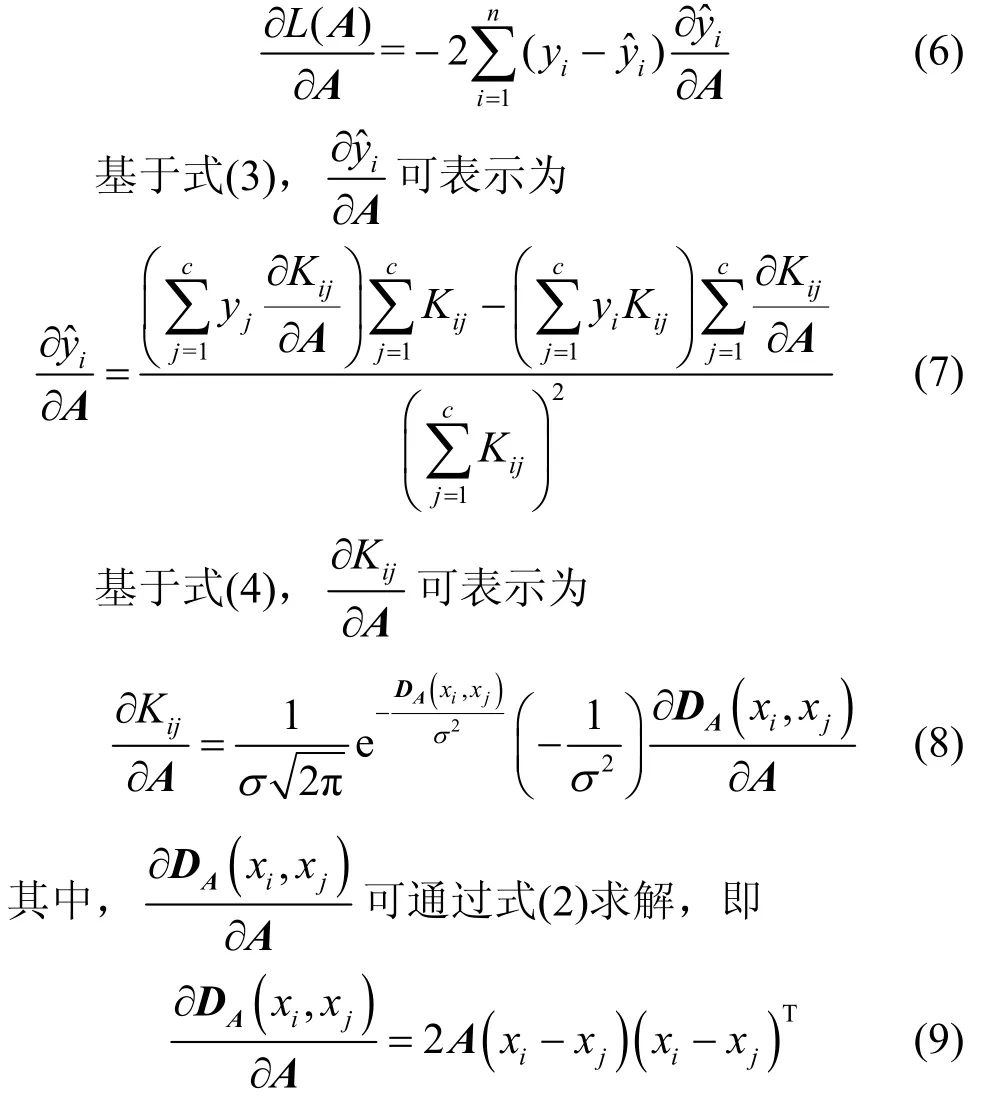
将式(7)～式(9)代入式(6)，可得

基于式(10)，利用梯度下降迭代更新映射矩阵A，即

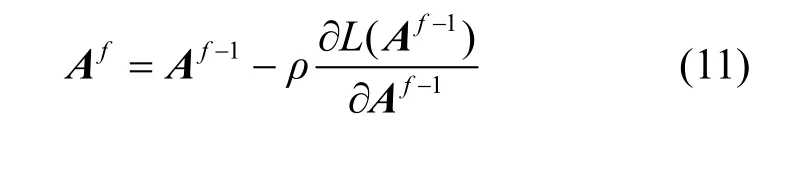
其中，ρ为学习速率，仿真中取值为0.001；f为迭代次数。将式(11)所得最优A代入M=ATA，则可求得最优M。实验中，A初始值可设为单位矩阵，为防止陷入局部最小值，可多次随机初始化[13]。

2.2 粒子滤波框架

作为复杂场景下目标跟踪的重要性采样技术，粒子滤波基于观测序列估计目标状态后验概率分布，以实现有效跟踪[17]。给定观测图像X1:r={x1,x2,…,xr}及其状态H1:r={h1,h2,…,hr}，可基于粒子滤波递归估计目标最优状态，即[18]

给定1～r帧观测结果X1:r，基于贝叶斯推理递归推导式(12)，以获得当前帧最优目标状态，可得

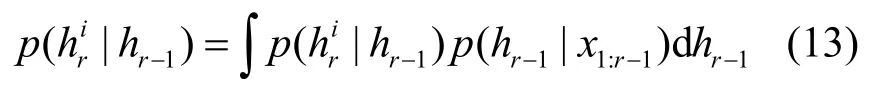
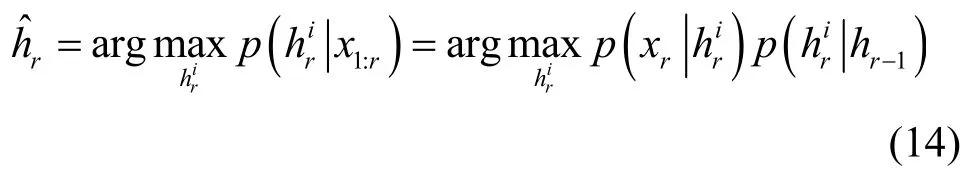
设时刻r的目标状态向量为为六自由度仿射变换参数，分别表示水平位移、垂直位移、旋转角度、水平尺度因子、扭曲角和宽高比例[19]。假设状态变量相互独立且服从高斯分布，则相邻帧间目标运动模型可构建为[19]

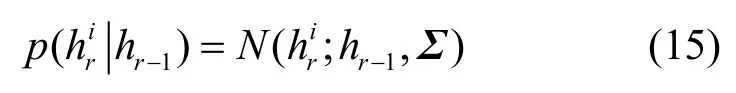
2.3 CNN 模型

CNN 以其优良的特征提取能力、强大的容错能力以及高效的计算效率，被广泛应用于图像识别、视频跟踪等领域[20]。本节基于具有卓越分类能力的AlexNet[21]构造视频跟踪特征深度提取模型（结构如图2 所示）。该模型输入图片规格化为227 ×227；为有效保留局部特征，权衡欠拟合及过拟合，第一卷积层中卷积核尺寸设置为11×11×96，步长为4，卷积核个数为64，以提取测试序列各类深层特征；权衡计算复杂度及特征抽取，第一卷积层后同时接3 个卷积层；设置第五卷积层中卷积核尺寸为3×3 ×256，步长为1，提取图像中目标背景样本作为后续度量学习样本；在第一、二和五卷积层后衔接尺寸为3×3、步长为2 的最大池化层，由于最大池化法较平均池化法可更好地提取纹理信息，因此本节采用最大池化方法以降低计算复杂度、提升模型稳健性并保留关键信息；第五卷积层后衔接3 个全连接层，以充分融合样本信息；基于全连接层所得融合特征，分类层采用Softmax 函数对其分类以区分目标背景；卷积层激活函数均采用ReLU 函数，且于卷积层后增加归一化层以降低过拟合。所提深度特征提取模型基于给定运动目标测试序列离线训练AlexNet 网络，以提升其泛化能力进而改善目标跟踪性能。

图2 CNN 结构

2.4 基于局部结构化评估的目标跟踪

视频跟踪中，评估候选目标与真实目标之间相似度可为后续候选目标选择提供合理依据并改善目标状态估计性能。候选目标相似度评估准则主要包括以下2 类：整体评估和局部结构化评估。整体评估准则适用于局部特征要求不高、图像整体区分度较小的场合；相较于整体评估方法，局部结构化评估更关注区域噪声和部分遮挡等局部细节，因而复杂环境下局部结构化评估准则更具稳健性[22]。需要注意的是，在目标跟踪过程中，图像局部细微变化都将影响跟踪效果。基于此，本节采用局部结构化重构误差评估准则衡量候选目标相似度。设m个候选目标Y=[Y1,Y2,…,Ym]可由包含w个模板的模板集T=[t1,t2,…,tw]表示。为避免局部变化导致跟踪精度降低，将每个模板分割为W个局部块，则模板集的第g个局部块可表示为Tg=[t1g,t2g,⋅⋅⋅,twg]∈，其中，tig,i=1,2,…,w为第i个模板的第g个局部块。类似地，将候选目标Yg分割为W个局部块{yg|g=1,2,⋅⋅⋅,W}∈Rb×1，利用特征映射A对每个yg进行核回归距离度量。由于局部遮挡、光照变化等干扰因素导致的目标表观变化具有空域稀疏性，由此可构建如下基于局部化模板集的候选目标最优稀疏表示问题

式(16)所示问题可视为W个问题的累加，且各变量相互独立，由此，可将此问题拆分为W个子问题，即

综上所述，对应候选目标重构误差可表示为

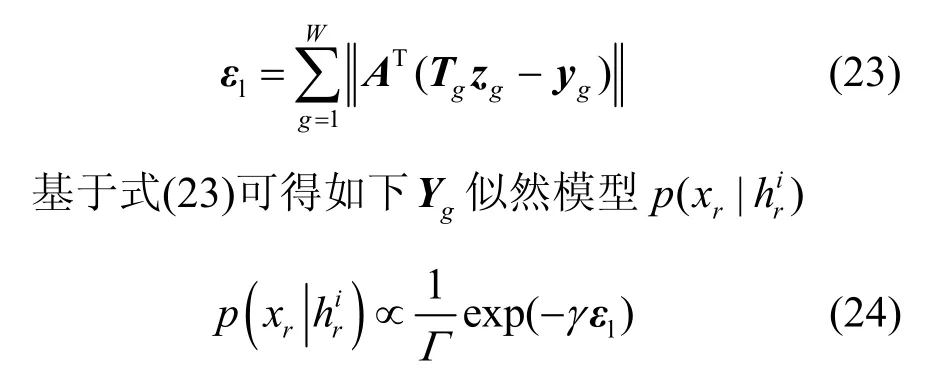
其中，Γ为归一化因子，γ为高斯核控制参数，仿真取0.01[12]。

2.5 在线更新策略

在实际跟踪过程中，模板固定不变无法有效跟踪复杂场景下多变的目标，因而模板更新是在线跟踪的关键一环[11]。若基于固定模板实施跟踪，则光照变化或部分遮挡等因素导致跟踪器无法较好地捕捉目标；反之，若快速更新模板，每次更新都会引入误差，则随着时间流逝误差逐渐累积，从而导致跟踪器偏离目标。针对上述问题，本节提出短时与长期稳定更新相结合的在线跟踪策略，以更新目标模板。

模板初始化。首先确定目标首帧所处位置，而后基于所提跟踪方法获得前n帧跟踪结果并归一化，最后将其组合为模板集T=[t1,t2,…,tn]∈Rb×n。

模板动态更新。模板与跟踪结果相似性可表示为ψ=[ψ1,ψ2,⋅⋅⋅,ψn]，设阈值为η，则跟踪结果与第i个模板相似性ψi可表示为

设最大相似度为Λ，其可表示为

将其与阈值η比较，若Λ＞η，表明本次跟踪结果与某目标模板相似度最大，则更新对应模板；反之，不进行更新。仿真实验中阈值取值为η=0.7。综上所述，具体更新方案可表述如下。

短时更新。为提高目标状态估计性能，对首帧后续各帧，若Λ＞η，表明该模板与某目标相似度最大，为提高后续各帧的跟踪准确度，可用本跟踪结果替换对应模板，并保存跟踪所得目标状态；反之，则表明相邻帧变化较大，此时不更新模板。

长期稳定更新。连续多帧所得最大相似度值Λ＜η，导致无法及时更新模板，此时连续多帧最大相似度均小于阈值，从而加大多帧累积误差，针对此类情况，可于跟踪过程中每隔10 帧更新模板。由于起始帧目标始终真实，所提更新策略需包含首模板以增强跟踪稳健性。

综上所述，结合粒子滤波与度量学习的目标跟踪算法详细步骤如算法1 所示。

算法1结合粒子滤波及度量学习的目标跟踪算法

输入测试序列I={I1,I2,I3,…,In}，粒子数N，映射矩阵A以及度量矩阵M

输出跟踪结果目标位置

1) 初始化CNN，粒子初始权重均设为1/N；

2) 采集首帧目标背景样本，并通过式(11)实施MLKR 以获得最优映射矩阵A及度量矩阵M；

3) 基于CNN 和度量学习区分目标背景，并计算每个粒子置信度（权重）；

4) 基于APG 方法，迭代更新式(20)、和式(22)直至满足收敛条件，从而获得最优稀疏系数向量zg；

5) 基于式(23)、式(24)与式(12)获取目标状态最优估计，并实施在线跟踪；

6) 获得跟踪结果，基于式(25)和式(26)计算本次跟踪最大相似度；

7) 若跟踪最大相似度大于阈值，则用本帧跟踪结果更新模板；反之，不进行更新；

8) 若跟踪最大相似度持续小于阈值，为防止跟踪累计误差过大，可每隔10 帧更新目标模板；

9) 判断是否跟踪至最后一帧，若没有，重复步骤3)～步骤8)；反之，结束跟踪，获得最终跟踪结果并保存所得目标框。

3 实验结果分析

目前，视觉跟踪领域数据集主要为OTB-100 和VOT-2018，分别包含100 个和60 个测试序列[24-25]，各序列皆面临不同跟踪挑战，包括光照变化、尺度变化、遮挡、形变、运动模糊、旋转及背景复杂等，且多数序列包含2 种以上影响算法性能的因素[25]。

基于上述数据集，本节选择包含多种跟踪挑战因素的MotorRolling、Jogging、Boy、Skating1、Matrix、Bird2、Tiger2、Basketball、Singer1 及Singer2共10种测试序列作为测试集（各序列主要挑战因素如表1所示），通过与CNN-PF[26]、Struck[27]、CT[28]、TLD[29]、DFT[30]、BACF[31]等主流跟踪器对比，以验证所提方法的有效性。实验硬件环境为处理器i5-4258、主频2.4 GHz、内存8 GB；软件环境为Python3.7、MATLAB 2017a、深度学习框架Caffe。

所提跟踪算法在首帧提取的正负样本数分别为100 和400，后续各帧正负样本数分别为30 和120。权衡跟踪性能及计算复杂度，若粒子过多则会增加算法计算量，过少则无法获取最优目标状态，因此，每帧粒子数设为600，粒子权重初始化为1/600。所提跟踪算法在首帧提取的正负样本数分别为100 和400，后续各帧正负样本数分别为30和120。权衡跟踪性能及计算复杂度，若粒子过多则会增加算法计算量，过少则无法获取最优目标状态，因此，每帧粒子数设为600，粒子权重初始化为1/600。CNN 结构如图2 所示，采用深度学习框架Caffe，基于Imagenet 数据集训练所得模型，而后利用OTB-100 及VOT-2018 微调参数，从而获得可有效提取特征的离线网络，权值更新采用梯度下降法，设置局部区域归一化参数α=0.0001，τ=0.75，以起到侧抑制作用；学习率设为0.001，训练周期为300，以最大程度减少过拟合发生。

3.1 定性分析

图3 为10 种测试序列的7 种跟踪算法的结果对比。MotorRolling 序列包含快速运动、背景杂波和光照变化等挑战因素，第52 及64 帧中目标由空中下降明显变化，DFT 和TLD 出现跟踪漂移或跟踪框与真实目标不符现象，而所提方法始终可较好地跟踪目标，原因是所提方法考虑背景杂波及快速运动影响并对目标背景样本进行误差学习，从而精确估计运动目标。Jogging 中目标存在明显遮挡，所提方法与TLD 及BACF 可定位目标并有效跟踪，其余算法出现跟踪丢失现象，表明部分遮挡条件下所提方法也具有较好的跟踪效果。Boy 中目标快速运动，同时出现比例变化和旋转等因素干扰，401 帧之后CT 出现跟踪漂移现象，原因在于其泛化能力较差，无法较好地适应显著外观变化，而所提方法始终可精确跟踪。Skating1 属于较复杂场景，目标背景对比度较低，且存在较强光照变化。此场景下目标分辨率较低，CT、DFT 及TLD 均出现目标丢失，原因是目标背景相似性较大，对比方法无法有效区分相似目标背景；而所提方法通过长短时结合在线更新策略及时更新模板，从而可有效区分目标背景进而实现稳定跟踪。然而，某些特殊场景下训练数据量较小，从而使网络参数无法获得最优值，导致跟踪中平均中心位置误差稍次于CNN-PF。由于Matrix 序列光照变化较大，对比方法均出现跟踪丢失现象，而所提方法仍可较好地锁定目标，这是由于所提方法基于MLKR 精准度量目标背景距离，并有效判别跟踪结果以确保最优候选目标得

以选择。快速运动导致运动模糊情况下，Bird2中目标外观尺度同时发生较大变化，Struck 及DFT 无法准确估计目标尺度，从而导致跟踪失败，而所提方法可自适应目标尺度变化因而仍可锁定目标。Tiger2 出现严重遮挡以及强背景杂波，对比方法均发生不同程度漂移或跟踪框与真实目标尺度不符，所提方法仍能稳定跟踪目标，且具有较高跟踪精度及稳健性，这是因为所提方法通过引入重构误差构建似然模型且采用局部化模板方法以解决目标遮挡和背景杂波，所以具有较强稳健性。由图3 可知，基于数据集VOT-2018测试序列Basketball、Singer1 和Singer2 所得结果与上述结果类似。Singer2 序列平均中心位置误差稍次于CNN-PF，原因与序列Skating1 相似，不再赘述。

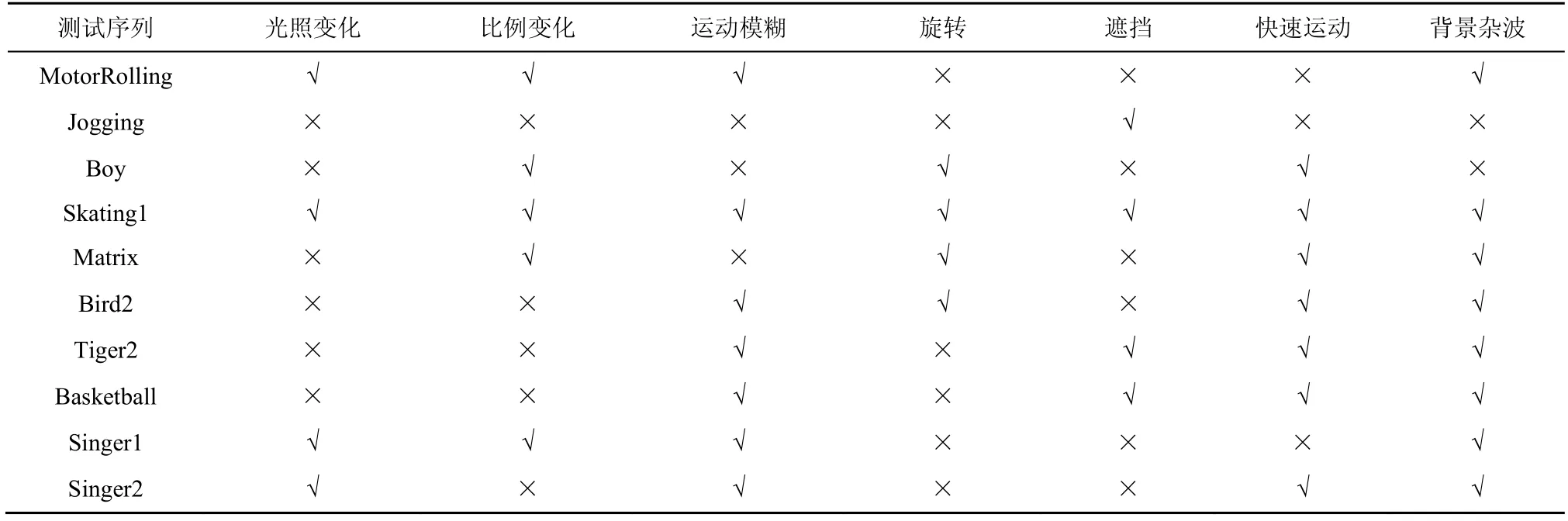
表1 测试序列及其主要挑战因素

图3 7 种不同跟踪方法的跟踪结果

3.2 定量分析

本节采用平均跟踪重叠率和平均中心位置误差定量分析所提方法性能。平均中心位置误差为真实位置(x0,y0)与估计位置(x1,y1)之间距离，即

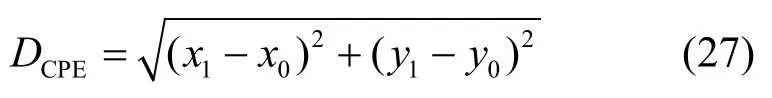
平均跟踪重叠率表示为

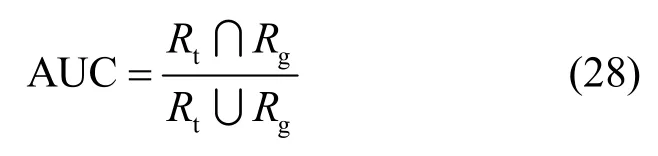
其中，Rt、Rg分别为跟踪结果及真实目标的面积。

表2 和表3 分别为不同跟踪方法在各测试序列的平均跟踪重叠率与平均中心位置误差。其中，加粗字体及下划线分别为性能最优及次优值。重叠率越大，中心位置误差越小，跟踪效果越好。

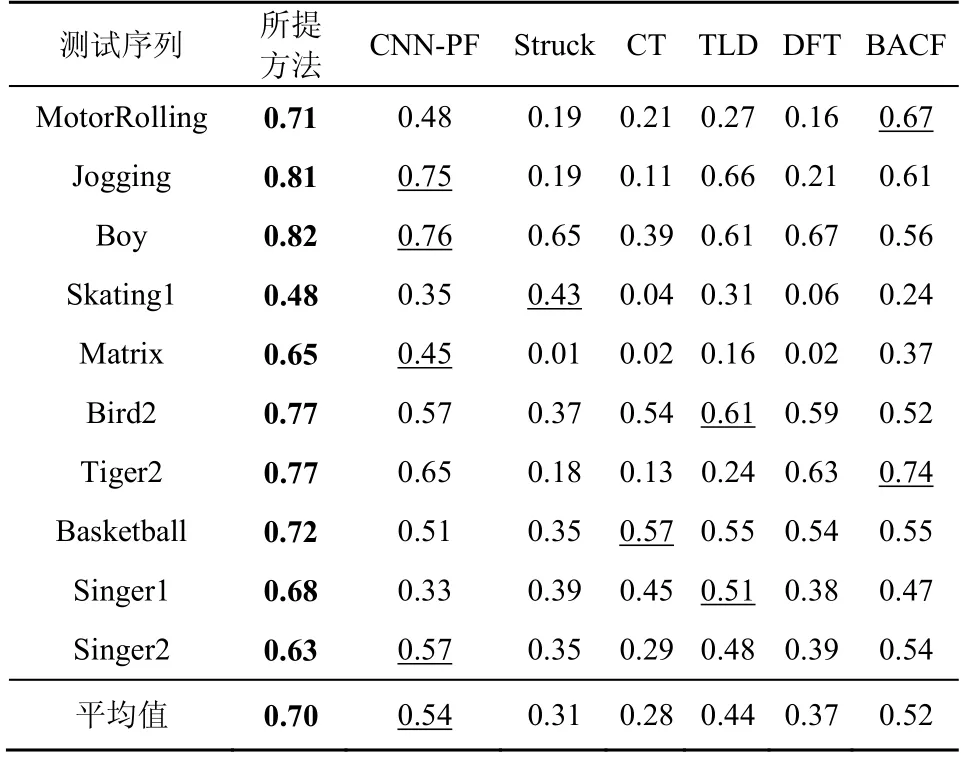
表2 不同跟踪方法在各测试序列的平均跟踪重叠率

由表2 和表3 可知，基于OTB-100 及VOT-2018所选10 种测试序列，所提方法相较于对比方法均有较好的跟踪效果，其可归因于所提方法采用MLKR 并引入误差项构建似然模型以降低相似目标背景之间敏感度。相较于对比方法，所提方法在遮挡及噪声等条件下性能出色，主要原因可表述如下。

表3 不同跟踪方法在各测试序列的平均中心位置误差

1) 所提方法考虑候选目标模板之间相关性，提高了复杂场景下算法跟踪稳健性。

2) 核回归距离度量衡量粒子相似性，从而提升跟踪有效性。

3) 目标模板局部结构化表示改善了噪声及遮挡场景下所提方法的稳健性及跟踪精度。

基于平均跟踪重叠率和平均中心位置误差指标，采用成功率曲线和整体精度曲线评估跟踪器整体性能[12]。成功率曲线表示将重合率大于给定阈值的帧作为成功跟踪帧，当阈值从0 变化到1 时，记录成功跟踪帧数占总帧数的比率；整体精度表示中心位置误差在距离阈值内成功帧数与总帧数的百分比[12]。不同跟踪方法跟踪成功率及整体精度曲线分别如图4 和图5 所示。由图4 可知，多数序列中所提方法跟踪成功率高于对比方法；Skating1 序列中所提方法相较于Struck 成功率偏低，而整体跟踪精度（如图5 所示）仍优于Struck；Tiger2 序列中所提方法跟踪精度略次于BACF，而跟踪成功率仍优于BACF；此外，其他序列中所提方法整体跟踪精度也优于对比方法。由此可知，复杂场景下所提方法整体性能优于对比方法，且具有较好的稳健性。

图4 不同跟踪方法跟踪成功率曲线

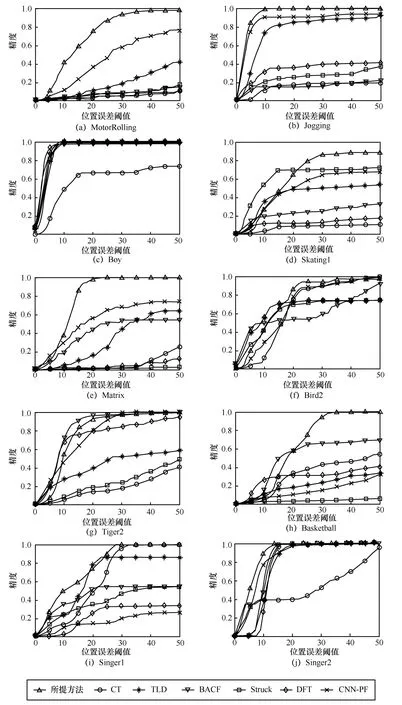
图5 不同跟踪方法跟踪整体精度曲线

为验证复杂场景下所提方法的稳健性，选取序列Boy 与MotorRolling 进行时间稳健性评估（TRE,temporal robustness evaluation）与空间稳健性评估（SRE,spatial robustness evaluation），对比结果如图6和图7 所示。由图6 和图7 可知，相较于对比方法，所提方法在光照变化、杂波等复杂背景下仍可有效跟踪目标，此可归因于所提方法优化所得度量矩阵可改善模板及候选目标之间相似性度量，模板局部结构化稀疏表示可显著抑制杂波及噪声，模板更新策略可有效抑制杂波、噪声、光照变化及遮挡等影响，从而复杂场景下所提方法跟踪稳健性相较于对比方法也可获得明显提升。

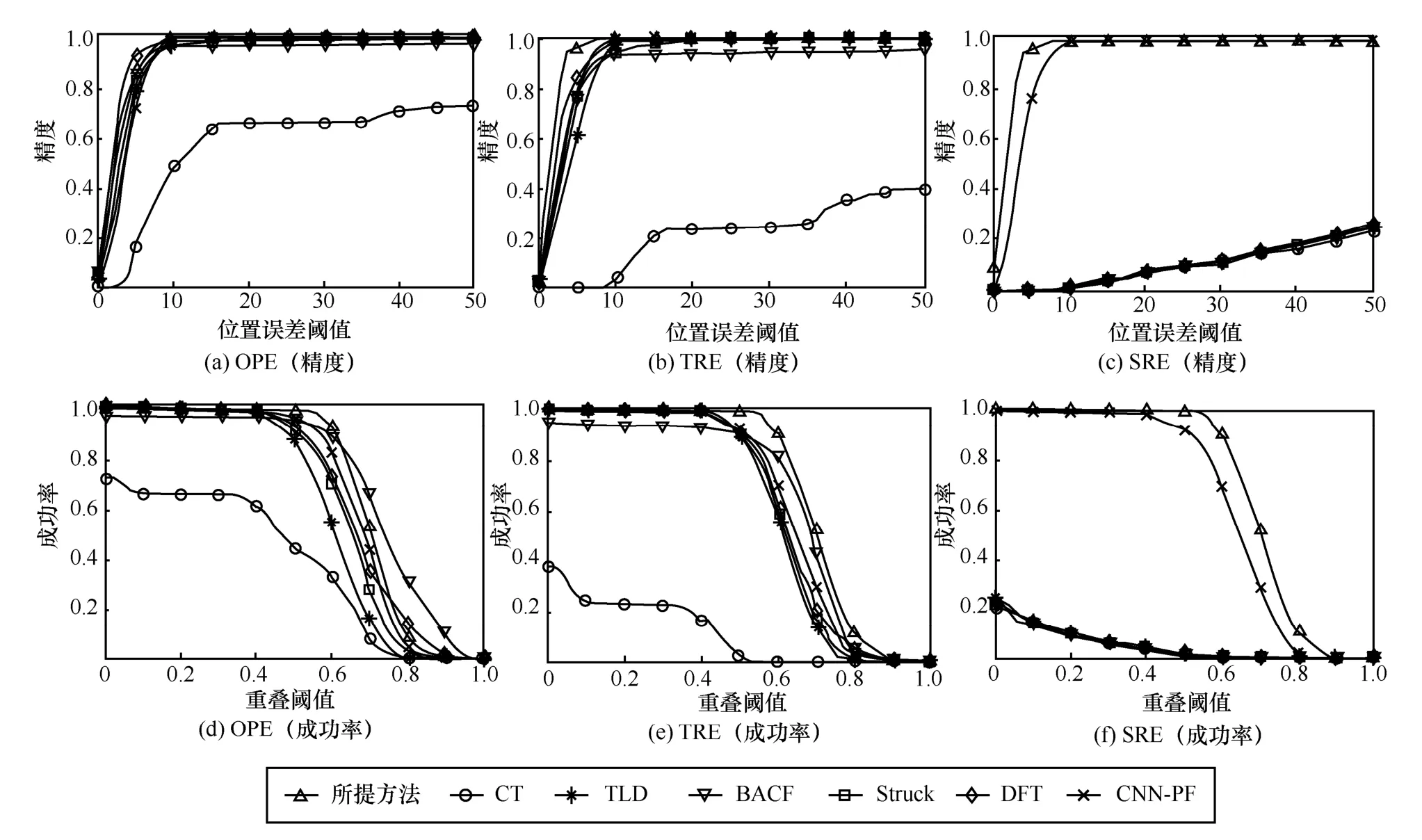
图6 序列Boy 场景下不同跟踪方法稳健性评估

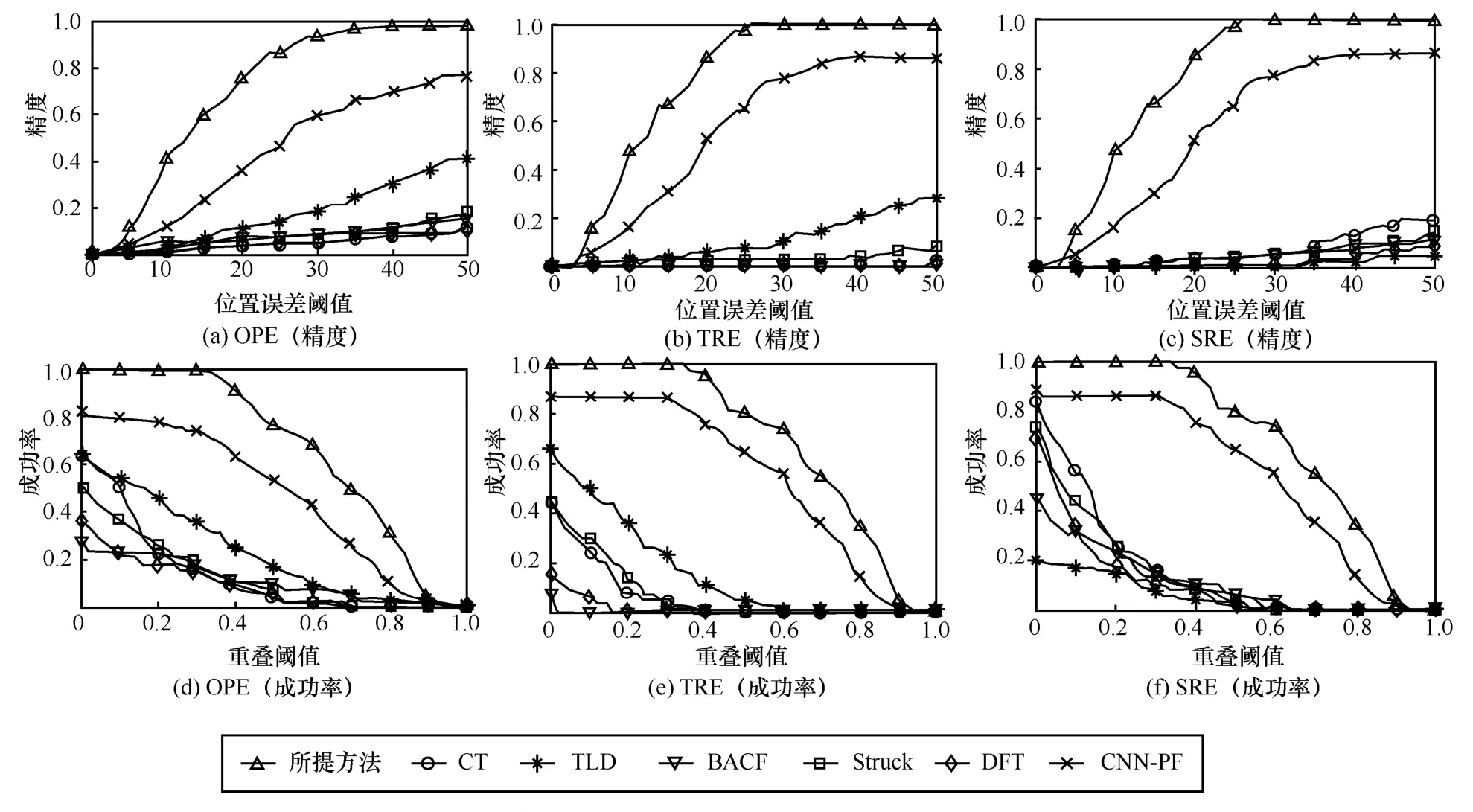
图7 序列MotorRolling 场景下不同跟踪方法稳健性评估

为验证所提方法各模块的有效性，基于测试序列Boy 与MotorRolling 的仿真结果如表4 所示。由表4 可知，MLKR 跟踪精度可平均提升0.065，粒子滤波跟踪精度可平均提升0.045，长短时更新跟踪精度可平均提升0.02，这表明度量学习及CNN融合模块、目标稀疏表示模块以及长短时更新策略模块均可有效提升视觉跟踪性能。

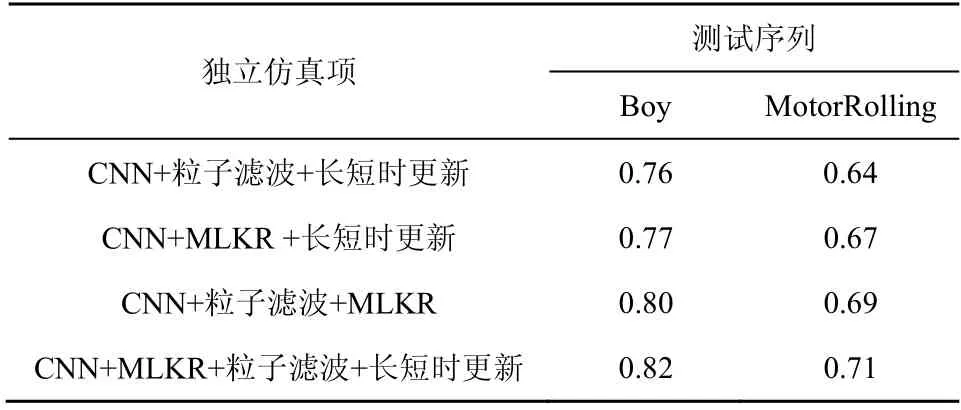
表4 基于测试序列Boy 和MotorRolling 的仿真结果

此外，为验证所提方法的跟踪时效性，本节采用每秒运行帧数（FPS,frame per second）衡量算法速度（运行50 次，平均所得FPS 作为评估指标），不同测试序列中各跟踪方法的FPS 如表5 所示。由表5 可知，所提方法速度高于CNN-PF、Struck 及DFT，低于CT、TLD 及BACF。然而，正如前文所述，各测试序列中所提方法跟踪性能整体优于对比方法。需要注意的是，基于粒子滤波的跟踪算法计算复杂度通常正比于候选粒子数量，因此，可通过先验或时间序列信息自适应调整粒子数量以降低复杂度，从而较好地均衡跟踪性能以及实时性。

表5 不同测试序列中各跟踪方法的FPS

4 结束语

针对目标形变等因素导致跟踪性能显著下降的问题，本文提出了融合度量学习与粒子滤波的跟踪方法。所提方法通过CNN 提取正负样本，并基于MLKR 对其度量学习后构建观测模型，然后基于短时及长期稳定更新相结合更新策略更新目标模板。基于OTB-100 及VOT-2018 数据集所选包含遮挡及光照变化等因素的10 种测试序列，通过与BACF、CNN-PF、Struck、CT、TLD 以及DFT 这6 种主流跟踪器对比验证了所提方法的有效性。由定性分析可知，所提方法在部分遮挡、光照变化、目标形变等复杂场景下具有较强稳健性；基于定量分析可知，相较于对比方法，多数测试场景下，所提方法平均中心误差较低，平均重叠率较高，这表明所提方法整体跟踪性能较优。