基于散射体信息的室内NLOS 多站协作定位算法

谢良波，李升，周牧，李泽，田增山，王亚，付长友

（重庆邮电大学通信与信息工程学院，重庆 400065）

1 引言

随着无处不在的基于位置服务的发展，智能产业的普及加速了室内场景中智能应用的过程[1-3]。考虑到大量的人类活动发生在室内环境中，因此，实用的基于位置的室内服务目前吸引了研究人员的大量研究[4-5]。受卫星信号覆盖范围的限制，在室外得到广泛应用的全球定位系统在室内无法发挥出应有的性能，因此，在过去的20 年中已经提出了多种室内定位技术。现有定位技术大致可以分为基于视觉的[6-7]、基于传感器的[8]和基于无线的，主要包括Wi-Fi[9-10]、蓝牙[11-12]、超宽带（UWB,ultra wide band）[13-14]等。在室内环境下，由于障碍物的遮挡无线信号会产生折射和散射，此种现象称之为非视距（NLOS,non line of sight）传播。尽管如此，当前基于Wi-Fi 的定位方法主要集中于视距（LOS,line of sight）场景，而在NLOS 环境中还没有比较好的解决方案。

在NLOS 干扰较严重的室内环境下，传统的LOS 定位算法将不再适用。基于此，出现了一些方法，如传播模型法、基于散射体信息法等。目前，传播模型法大部分基于经典散射模型。文献[15]提出了一个推导的散射模型，包括圆环模型、圆盘模型以及椭圆模型的到达角（AOA,angle of arrive）、飞行时间（TOF,time of flight）概率密度函数的方法。由于室内场景大小的限制，大部分散射模型仅仅适用于室外的蜂窝网定位，因此在室内环境下传播模型法应用较少。而基于散射体几何位置关系的定位算法，其巧妙之处在于把NLOS 干扰带来的定位误差转换为可用的物理测量因素，因此定位精度主要取决于定位参数的测量精度。文献[16]提出了一种定位方法，该方法利用4 个基站，其中3 个作为定位基站，剩下的一个作为辅助基站，通过AOA和TOF 的测量值计算散射体的位置，并以此确定目标到散射体的距离，由于散射体到目标之间不存在障碍物，因此利用散射体作为虚拟基站，通过传统的LOS 定位方法完成对目标的定位。然而该方法中以散射体为虚拟基站是建立在信号经过散射体后为镜面反射的基础上，要求散射体表面足够大且光滑或者信号波长足够小，但实际情况中很难满足该条件。因此，这种方法在UWB 定位中应用较多，并且在一般的商用网络中，收发双方往往是不同步的，因此以上基于绝对TOF 测量的定位算法在大多数场景中都不太实用。针对上述问题，本文提出一种室内NLOS 环境下多站协同的定位算法，可在完全没有LOS 路径的情况下对目标进行定位。本文主要的研究工作如下。

1) 建立了一种多站协作的室内NLOS 定位算法。区别于传统的抑制多径信号的方法，本文算法将NLOS 路径作为定位路径，可以在完全没有LOS信号、散射体位置未知的情况下完成定位，并且还消除了相位误差对TOF 的影响，解决了现有的室内定位系统至少需要一条LOS 路径的问题。因此，该算法可应用于现有的商用Wi-Fi 和LTE 网络。

2) 由于缺少出射角（AOD,angle of departure），将导致散射体的位置出现较大的位置模糊。为了解决这个问题，本文算法充分利用多个接入点（AP,access point）的优势，结合房屋结构的先验信息，并利用多个AP 相互协同缩小了散射体的模糊范围，从而限制了散射体区域。此外，定位方程的求解使用了列文伯格马夸尔特（LM,Leverberg Maquardt）算法。

3) 提出了一种基于遗传算法（GA,genetic algorithm）和LM 混合求解算法。传统LM 算法的收敛性能取决于迭代初始位置。为了解决这一问题，本文首先采用GA 对目标的位置进行粗略估计，利用其全局优化能力可以自适应地调整搜索方向这一特性，以获得目标的全局近似解，并作为LM 算法的迭代初始位置。仿真结果表明，该混合算法可以有效提高定位精度。

2 信号模型

反映信号传播特性的信道冲激响应（CIR,channel impulse response）可以表示为

其中，αn为第n条路径的幅度，τn为第n条路径的TOF，fD为多普勒频移，由于室内的目标移动速度通常很慢，因此多普勒频移很小，可简化为

对式(2)进行傅里叶变换，得到的信道频率响应（CFR,channel frequency response）为[17]

其中，N为路径的个数，f为信号的载波频率。假设每个AP 均有P根天线，组成的线性天线阵列如图1 所示。

图1 线性天线阵列

采用正交频分复用（OFDM,orthogonal frequency division multiplexing）调制，子载波数量为K，AP 上所有天线的全部子载波的CFR 矩阵可以表示为

由联合角度和时延估计模型[18-19]可知，H又能表示为

其中，E是PK× 1维的噪声矢量，S是N× 1维的衰减矢量，A(θ,τ)是PK×N维的导向矩阵，可以进一步表示为

其中，⊗表示克罗内克（Kronecker）积，a(θ)和b(τ)可分别表示为

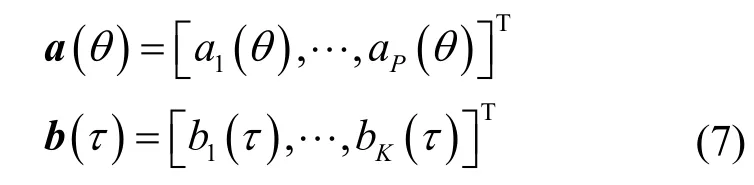
式(10)是一个Lp-norm 的优化问题，理想的稀疏度度量是L0范数，表示的是中非零元素的个数。然而，当本文使用L0-norm 来求解式(10)时会发现这是一个NP-hard 问题。为了解决这个问题，可以使用L1-norm 作为L0-norm 的近似值，对于L1-norm 优化则是一个经典的凸优化问题。文献[21]中提到通过调整参数λ，可以在和之间的最优权衡曲线上移动，由此得到之间的稀疏性或非零元素个数之间最优权衡曲线的近似，采用二次锥规划可以很好地解决该优化问题，最终得到AOA 和TOF。

3 室内NLOS 多站定位模型

NLOS 环境下信号传播如图2 所示，其中虚线所示的LOS 信号直接沿直线传播，但是当目标和AP 之间存在障碍物遮挡时，LOS 信号将不复存在，此时，收发双方处于NLOS 环境中，无线信号会经过散射体散射之后再被AP 接收到，此现象被称之为NLOS 传播。信号波长与散射体尺寸会影响NLOS 信号传播特性，如果散射体尺寸大于信号波长，则为反射；如果小于，则为散射。为了提高定位方法普适性，本文中NLOS 信号均为散射信号，反射情形下的角度估计是散射情形下的特殊情况，所以本文的NLOS 定位模型对于反射信号依然适用。

图2 NLOS 环境下信号传播

在日常生活中（如会议室、教室、商场等常见环境），当环境中AP 被障碍物完全遮挡而不存在LOS 信号或者房间内部没有布置AP，而需要通过房间外的AP 对房间内目标进行定位时，此时，利用传统的依赖于LOS 信号的定位方法往往达不到理想精度要求。针对上述问题，本文构建如图3 所示的普适性较强的室内NLOS 定位场景，并提出相应定位方法。

图3 中，射线表示信号的反射路径，待定位目标位置坐标记为u(x,y)，编号为n的AP 以及第i个散射体分别记为假设每个AP 接收到经由M个散射体反射后的路径。房间的长、宽分别为L和W，左右两侧门的坐标分别为中间为墙壁。

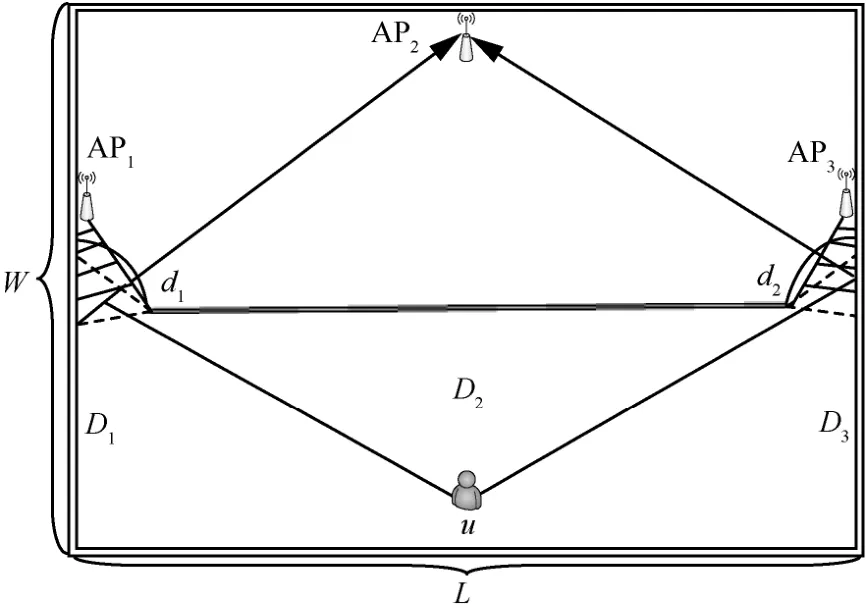
图3 室内NLOS 定位场景

首先根据AP1、AP3以及d1、d2的位置信息，协同确定AP1和AP3的LOS 区域和NLOS 区域。A P1到点d1的直线方程为

其中，k1、b1分别为直线的斜率和截距。因此，AP1的LOS 区域可确定为

同理，AP3的LOS 区域可确定为

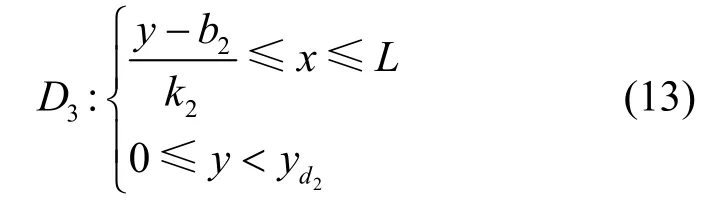
其中，k2、b2分别为两点所确定直线的斜率和截距。针对LOS、NLOS 混合的场景，也就是当目标u位于D1、D3区域时，AP1、AP3便能检测到来自目标的能量较强的LOS 信号，此时，可利用混合场景下的定位算法[22]。结合式(12)与式(13)，即可进一步估计出NLOS 区域，对应于模型中的D2区域，当定位目标u位于D2中时，此时3 台AP 皆没有来自目标的LOS 路径，因此只能通过散射信号进行定位。其表达式为

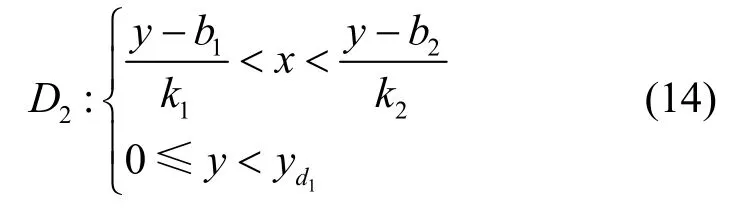
其次，利用多个AP 相互协作缩小散射体的模糊范围，结合房屋结构先验信息确定散射体的存在区域，对应于模型中的阴影部分区域。根据连接d1和AP3以及d2和AP1的直线，分别确定散射体区域的下边界，可表示为

其中，k3、b3分别为两点d1、AP3所确定直线的斜率和截距，k4、b4分别为两点d2、AP1所确定直线的斜率和截距。由于目标的方向和位置未知，因此无法准确计算出散射体区域的上边界，但能够根据AP 布局与房间先验信息对散射体区域的上边界进行近似估计，可表示为

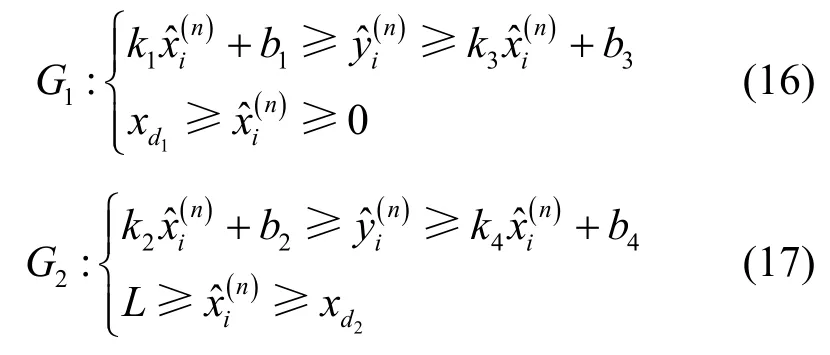
根据散射体的存在区域G1和G2，结合入射信号的AOA 将散射体的位置进一步约束到区域中的线段上，再从约束线段上搜索散射体的位置，后续用于建立定位方程组。由前面的假设可知，每个AP 接收到经由M个散射体反射后的路径，相应地，存在M条散射路径的AOA，因此能够确定散射体的约束线段，假设第i条路径的AOA为因此由AP 到散射体两点之间确定的直线方程为

结合散射体的约束区域，从而确定散射体的搜索范围，即散射体的约束线段，可表示为

由于G1、G2的上边界仅为一个估计值，因此线段Z1、Z2上还存在着模糊，需要再对线段进行进一步的约束。然而，在没有任何目标先验信息的情况下去除模糊是困难的，并且考虑到算法的复杂度，本文结合模型中的几何特征的方式去除模糊，图4 展示了各个AP 接收到的反射信号的传播路径。

图4 中，射线表示各个AP 接收的反射后的信号，通过对散射区域中的线段，也就是图4 中三角形区域中的线段取中间的方式去除大部分模糊误差，由此对散射体建立约束，可表示为

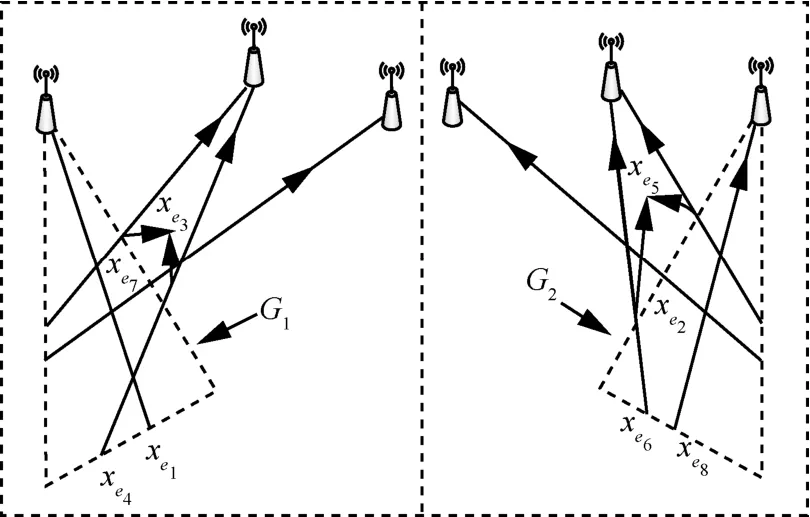
图4 各个AP 接收到的反射信号的传播路径

其中，c为电磁波在真空中的传播速度，τ(ϕCFO)为载波频率偏移（CFO,carrier frequency offset）引起的公共误差，Δτ为附加时延，εi为估计误差。由于发射机与接收机的时钟不同步以及晶振源存在细微的偏差，导致收发两端混频器产生的载波频率出现偏差，从而引入了部分系统相位误差τ(ϕCFO)和Δτ。但对于同一个AP 上接收到的多径信号而言，可以选取一个参考路径，将不同路径与参考路径之间进行差分消除相位误差的影响，并利用差分TOF建立定位方程。以第一条路径作为基准，将第i条反射路径与基准路径做差分，并将第i条路径相对于参考路径的差分TOF 记为，可表示为

其中，方程包含x、y2 个未知数，当等式的个数大于或等于未知数个数时即可联立求解。已知AP的个数为3 个，当M≥ 2，即各个AP 接收到的反射后的信号多于2 条时，式(24)为超定方程，通常，在室内环境下很容易满足。然而信号在室内NLOS环境中传播时，其TOF 与AOA 的估计值往往存在一定的相位误差，导致式(24)不总是准确的，因此本文提出通过差分的方式消除系统公共误差。基于理论上的差分TOF 方程(24)，然后和观测的差分TOF 构造误差最小化目标定位方程，差分TOF 的观测值记为，式(24)可改写为

基于以上分析，本文将确定方程求解问题转换为优化问题求解，可表示为

因此，对目标位置的定位估计可以通过最小化目标函数式实现，目标函数式可表示为

综上所述，结合目标的可行域D2，本文将定位问题转化为非线性最小二乘优化问题，可表示为

4 基于LM 的目标与散射体联合定位算法

对于本文的优化问题，可采用使用导数的最优化方法求解，如高斯牛顿（GN,Gauss Newton）法、LM 算法等。GN 法对初始点的依赖性很大，当初始点远离极小点时，牛顿方向在迭代过程中不一定是下降方向，导致GN 法很难收敛。LM 属于信赖域算法，继承了GN 法的优点，利用目标函数的雅可比（Jacobian）矩阵近似黑塞（Hessian）矩阵，节省了算法每步都需要计算Hessian 矩阵的额外开销，提高算法效率，并且通过引入单位矩阵，解决了近似Hessian 矩阵不一定可逆的问题。因此，本文利用LM 算法对目标的位置进行快速求解，主要包括以下几个步骤。

步骤1利用多个AP 相互协作并且结合房间先验信息确定散射体的模糊范围以及目标的可行域D2，再根据路径的AOA 得到散射体线段和，并在约束线段上按一定步长进行搜索，从而得到散射体的位置信息。

步骤2利用每条路径的飞行时间，根据计算出每条路径总长度的观测值，选取其中一条作为参考路径，计算其余路径与参考路径之间的路程差。

步骤3根据式(14)所示的目标可行域，从可行域中选取目标的初始点，确定阻尼参数u、放大系数v、参数β和精度eps，并根据实际情况进行适当调整[23]。

步骤4开始进入迭代，计算ψ(X)，由雅可比矩阵J根据式(27)得到，可表示为

步骤5根据JTΦ计算的梯度，通过求解式(31)计算目标函数的下降方向ϕ，可表示为

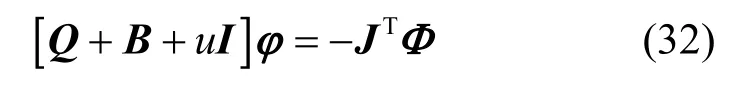
其中，B矩阵可通过BGFS 算法[24]中的修正公式计算得到。

步骤6根据Armijo-Goldstein 准则[25]计算步长λk，再利用式(33)更新目标位置，计算终止条件（norm(ϕ) ≤eps ）是否被满足。

①若满足终止条件则跳出迭代，使用当前的位置坐标X作为目标函数的最优解。

步骤7由于最后的迭代结果可能收敛于局部最优值，因此本文利用仿射传播聚类（APC,affine propagation clustering）算法[26]剔除误差较大的目标位置，聚类算法主要原理是根据目标位置之间的相似度将其分类，相似度定义为目标位置之间的负欧氏距离，以目标位置的相似度作为算法的输入，对式(34)与式(35)所定义的吸引度α与归属度ε不断地进行迭代，直到所有聚类中心的位置不再发生变化或者满足最大迭代次数。

其中，i表示目标位置点，j表示聚类中心，s(i,j)表示位置i与位置j之间的相似度。最后对聚类的算法输出取平均，作为最终的目标位置。

5 基于遗传算法的定位算法优化

经过多次实验观察，LM 算法的收敛性能好坏很大程度上取决于迭代初始位置，如果初始位置离真实目标位置较远，将导致最终的定位误差较大。如图5 所示，为AP 的摆放位置，连线为信号的传播路径，为散射体，为目标的真实位置，为目标初始位置，为LM 输出的最终位置，从图5(a)可以直观地看出，当初始位置的选取离真实位置较远时，此时可能会存在局部最优值，导致较大的定位误差；图5(b)展示了初始位置靠近目标真实位置时的情况，此时算法的收敛效果最好，具有较小的定位误差。为了解决这一问题，本文采用GA 对目标的位置进行粗略估计，获取一个目标的全局近似解，并以此作为LM 算法迭代的初始位置。

图5 初始位置对于LM 算法性能的影响

GA 具有全局寻优能力，能够自适应调整搜索方向等优点，且不需要复杂的求导运算，使算法的运行效率非常高，因此本文采用GA 来确定LM 算法的初始值。GA 的步骤包括初始种群的确定、适应度函数的设计，以及选择、交叉、变异等操作，GA 的性能主要取决于适应度函数的计算，结合目标函数式(28)，适应度函数可以设计为

种群的适应度越高，意味着方程的近似解越精确。当达到最大进化代数后，将适应度最高的种群作为GA 的全局最优解，并以此值作为LM 算法的初始值，进行二次优化求解，如图6 所示，其中，图6(a)和图6(b)分别为2 次不同位置的结果。

图6 GA 对目标初始位置的影响

综上所述，定位算法流程如算法1 所示。

算法1定位算法流程

输入AOATOF、房间先验信息、AP 位置

输出目标位置

6 仿真分析

6.1 仿真条件

为了分析所提的多站协同定位算法的性能，本节对本文所提算法进行仿真验证，仿真条件如下。设置房间的大小为20 m×30 m，其中左右两侧门的坐标分别为d1(1.5,8)、d2(27.5,8)，定位基站的坐标分别为AP1(0,11)、AP2(15,20)、AP3(30,11)，散射体个数为2个。根据模型的几何特征以及文献[27]的误差分布结果，确定AOA、TOF 的误差均为零均值的高斯白噪声，标准差分别记作σAOA=3°和σTOF=0.8 m，每个实验分别进行500 次独立仿真。

6.2 不同算法性能对比以及定位精度

本文选取文献[28]中所提的基于 AAT（AOD/AOA/TOF）的NLOS 定位方法以及文献[22]中的M3算法进行对比。图7 中展示了2 种算法与本文所提算法的定位误差累积分布。从图7 中可以看出，本文所提算法中值误差为2.63 m，而AAT算法和M3算法中值误差分别为3.13 m 和3.02 m。本文所提算法优于AAT 算法和M3算法，主要原因是AAT 算法利用绝对TOF 进行定位，因此对TOF的测量精度有比较高的要求，对于时钟不同步的收发方，想要获取精确TOF 非常困难，而M3算法在缺少LOS 路径时会出现位置模糊即存在局部最优值，同时2 种算法均额外利用了AOD，这对目标的硬件要求较高，因此算法的普适性受到影响。此外，从图7 中还可以看出使用GA 优化前后的性能对比，优化前后的中值误差从4.48 m 减少到2.63 m。

图7 不同定位算法的定位误差累积分布

6.3 散射体个数对定位精度的影响

本文所提算法对散射体材质没有任何要求，但散射体尺寸会影响NLOS 信号的传播特性[29]，散射信号的能量衰减较大，相比于反射信号来说定位精度会变低。传统的室内环境多为非光滑平面，其散射体尺寸较无线信号波长小，在室内环境中多为散射现象。因此，散射体的尺寸大小问题最终可归结为散射体数量的问题。散射体数量越多，意味着可建立的约束方程越多，因此增加散射体个数可以减少定位误差。图8 为不同散射体个数时的定位误差累积分布。从图8 中可以看出，当散射体个数为2、4、6 时，中值误差分别为2.63 m、2.12 m、1.86 m。随着散射体个数增加，定位精度也随之增加，当散射体个数从2 增加到4 时，误差减小较多，为0.51 m；当散射体从4 增加到6 时，误差减小较少，为0.26 m。

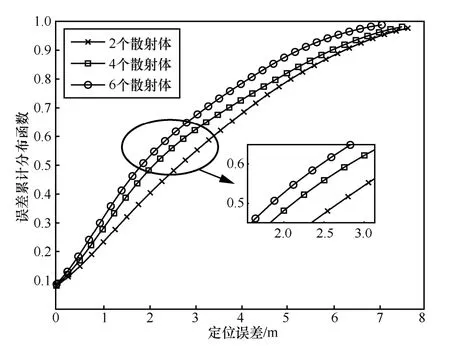
图8 不同散射体个数时的定位误差累积分布

6.4 房间结构对算法的影响

本文根据AP 的位置以及房间内墙壁构造几何约束，进而限制散射体的模糊区域以及目标可行域，当房间中墙壁的长度减小时，散射体的模糊区域会随之增大，但目标的可行域却会减小；当房间中墙壁的长度增加时，散射体的模糊区域会随之缩小，但目标的可行域会随之增大。图9 为不同墙壁长度时的定位误差累积分布。从图9 中可以看出，当房间内的墙壁长度为27 m、28 m 和29 m 时，中值误差分别为2.77 m、2.72 m 和2.63 m，由此可知，墙壁长度的长短对定位的精度影响非常小。

图9 不同墙壁长度时的定位误差累积分布

6.5 AP 摆放位置对算法的影响

为了验证AP 摆放位置对定位精度的影响，通过改变AP1和AP3的纵坐标位置并始终保持来观察其影响，图10 为AP1和AP3不同纵坐标时的定位误差累积分布。从图10 中可以看出，当纵坐标位置为9 m、10 m、11 m、13 m 时，中值误差分别为1.98 m、2.18 m、2.63 m、2.63 m。随着AP1和AP3纵坐标位置下移，定位精度总体呈增加趋势，当纵坐标位置从11 m 减少到10 m 时，误差增加较多，为0.40 m，之后误差波动范围较小。结合图2 来观察这个过程，当纵坐标逐渐增大，也就是AP1和AP3离房间中间的墙壁越远时，散射体模糊区域和目标可行域都会增大，因此会在一定程度上降低定位精度。

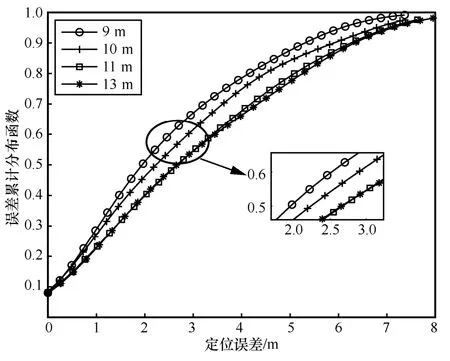
图10 AP1 和AP3 不同纵坐标时的定位误差累积分布

6.6 AOA 误差和TOF 误差对定位精度的影响

为了验证参数估计带来的AOA 和TOF 误差对定位精度的影响。表1 展示了在不同AOA 和TOF误差下的定位精度，为了表述方便，本文使用距离单位表示TOF，使用均方根误差（RMSE,root mean square error）来衡量定位性能。可以看出，AOA 和TOF 误差对定位精度的影响很小，其实这正是所提模型的优点所在。

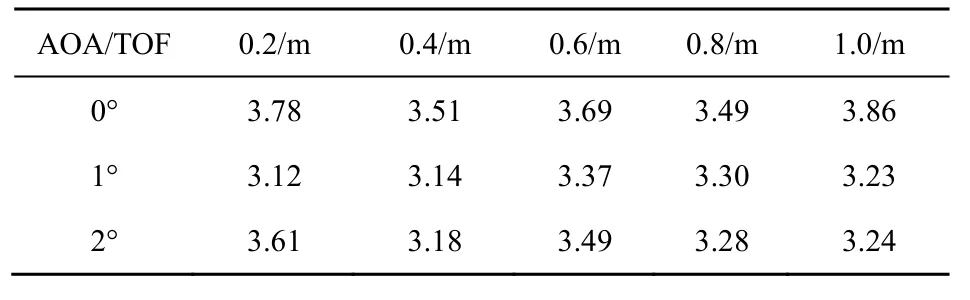
表1 不同AOA 和TOF 误差下的定位精度

为了验证该优点，进一步仿真以确认AOA/TOF 误差在相关约束条件下是否会影响准确性，如图11 所示，其中，图11(a)表示AOA 误差对应的误差累积分布，图11(b)表示TOF 误差对应的误差累积分布。当除去所提出的模型带来的约束时，定位精度将随着AOA/TOF 误差的增加而降低。

图11 AOA 和TOF 估计误差对定位精度的影响

7 真实环境模拟测试

7.1 复杂环境建模仿真软件Wireless Insite 介绍

由于采用现有商用设备无法搭建测试平台，因此为了进一步验证算法在实际环境中的性能，本文采用Wireless Insite 软件来模拟真实的室内环境，通过图形用户界面中实现室内传播建模，模拟真实的室内场景，分析发射机到不同区域的路径损耗和传播路径，最大程度上还原真实的测试。

Wireless Insite 是REMCOM 软件包中一款对复杂电磁环境进行建模仿真分析的软件，适用前沿的高频电磁处理方法，能够在50 MHz～100 GHz 的频率范围内提供准确的计算结果。根据一致性绕射理论（UTD,uniform theory of diffraction）和几何绕射理论（GTD,geometrical theory of diffraction），基于射线跟踪的方法构建信号在不同场景中的传播模型，还使用了2D、3D 和快速3D 的算法，根据无线信号经过物体反射或者绕射后的相关特征以及透射系数计算电磁场，并结合具体的天线模式来计算无线信号在传播过程中的损耗、到达时间和到达角等。因此该软件可以最大化地复现实际的室内或室外环境，以分析电磁波在环境中的传播特性。

文献[30]利用Wireless Insite 进行5G 信道建模，通过Wireless Insite 进行射线追踪模拟，并利用Ericsson 5G 试验台的测量结果验证了射线追踪模拟的准确性。文献[31]讨论了Wireless Insite 对无线电波传播的预测过程，并介绍了在与仿真相同的位置设置同样参数的实际测试环境，对仿真和实际测量的结果进行详细比较，最终通过质量和准确度的综合分析对Wireless Insite 软件进行验证，结果表明该软件能够最大限度地还原真实的测试。

7.2 模拟测试

模拟测试环境中无线信号载波频率为5.805 GHz（标准ISM 频段），因此在未来完全有可能运用到实际网络中。由自由空间损耗衰减模型可知[32]，载波频率越高，波长越短，意味着无线信号在传播过程中损耗会越大，在发射功率保持不变的情况下信噪比会降低，将对参数估计精度造成一定影响[20]，使AOA 和TOF 估计误差变大，从而导致定位精度下降。图12 展示了真实场景以及模拟测试场景。此次模拟实验在房间内设置了110 个目标点，对应图中的方块，在房间外布置3 个AP，其坐标分别为AP1(0，11 .4)、AP2(6.0，13 .9)、AP3(13.2，11 .2)，连线表示无线信号，两扇门宽度均为0.8 m，房间大小为13.3 m×13.9 m。

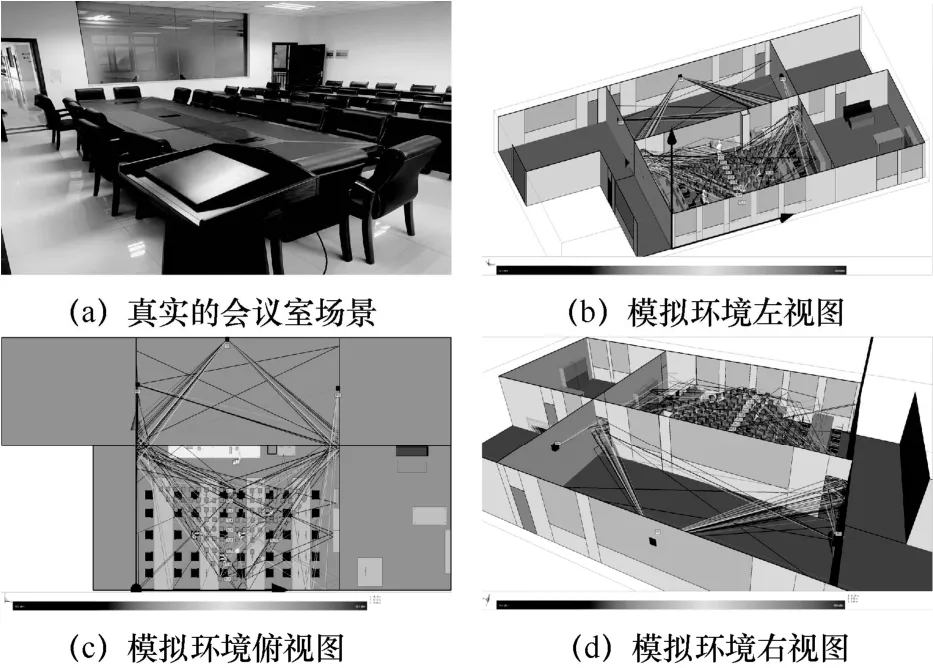
图12 真实场景以及模拟测试场景

模拟测试环境的定位误差累积分布如图13所示。从图13 中可以看出，中值误差为1.12 m，通过Wireless Insite 验证了算法在实际场景中的有效性。

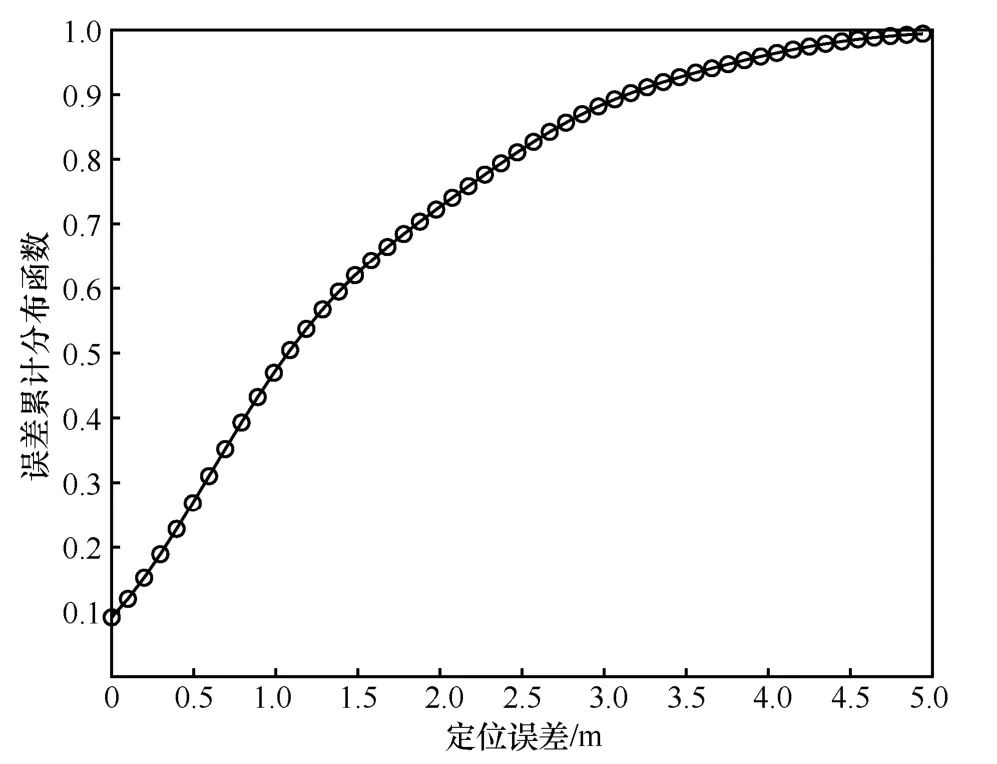
图13 模拟测试环境的定位误差累积分布

8 结束语

本文充分利用室内环境的结构信息及散射体分布特性实现定位，提出了一种利用多径信息的室内NLOS 多站协作定位算法。基于差分TOF、散射体估计值以及AP 位置，建立NLOS 定位模型，并利用GA 获得的目标的粗略位置，再通过LM 进行二次优化获取目标精确位置。仿真结果以及真实环境模拟测试结果显示，所提算法具有较好定位精度。