水足迹视角下世界主要经济体的水资源利用效率研究

刘云江 邓光耀

1 引言及文献综述

水是“生命之源、生产之要、生态之基”，但是近年来，世界各国对水资源的需求随着人口的增长和经济的发展而越来越多，另外从全球来说水资源时空分布不均，而水资源供给有限，从而导致了严重的水资源供求矛盾。提升水资源利用效率是解决水资源供求矛盾的必经之路。水资源利用效率可分为绝对效率和相对效率（邓光耀和张忠杰，2019［1］；邓光耀，2020［2］）绝对效率是指采用喷灌、滴灌等节水灌溉技术所能提高的水资源利用效率，相对效率是指相对于各决策单元（Decision-Making Unit，简称DMU）共同前沿面的效率。通常各国政策文件所提及的水资源利用效率是指绝对效率，例如中国政府在《关于实行最严格水资源管理制度的意见》中指出“到2030年，中国的用水效率应接近甚至达到世界先进水平，工业方面的万元工业增加值用水量降低到40立方米以下（以2000年不变价计算），农业方面的农田灌溉水有效利用系数提高到0.6以上”。学术界则通常研究相对效率，一般利用DEA（Data Envelopment Analysis）模型来测算水资源相对效率。

利用DEA模型来测算水资源利用效率，一般将水资源作为投入，经济增加值作为产出。一般情况下，经济产出的创造不止水资源一种投入，因此结合资本、劳动力等其他要素来测算水资源利用效率是必要的，例如Hu等(2006)［3］基于全要素视角测算了1997-2002年中国各省的水资源利用效率，指出中国中部地区水资源利用相对较低。由于水资源使用过程中会产生污水，因此有部分文献将污水看成非期望产出利用SBM-DEA（Slack-based Measure-Data Envelopment Analysis）模型（Bian等，2015［4］；Deng 等，2016［5］；Yang 和 Li ，2017［6］；Zhou 等，2018［7］） 或 者利用Seiford线性变换（Wang 等，2018［8］）来测算水资源利用效率；另外也有部分文献进一步考虑污水治理阶段的效率（Bian等，2014［9］）。由于农业用水量占比最大，部分研究者还利用DEA模型研究了农业用水效率问题（Lilienfeld和Asmild，2007［10］；Speelman 等，2008［11］；Frija 等，2009［12］；Chemak 等，2010［13］；Wang，2010［14］；Gadanakis等，2015［15］；Wang 等，2015［16］）。虽然已有的文献对水资源利用效率的测算做出了一定研究，但是在测算水资源利用效率时一般只考虑了蓝水的使用量（也即统计年鉴中给出的水资源使用量），忽略绿水和灰水使用量，也即缺乏从水足迹角度来测算水资源利用效率的研究。所谓水足迹，是指一个国家（地区、个人）生产（消费）的直接用水和间接用水的总和（Hoekstra 等，2011［17］）。水足迹可细分绿水足迹、蓝水足迹和灰水足迹，其中绿水是指作物根部土壤储存的水（主要是雨水），蓝水是指有经济价值的江河、湖泊、地下水，灰水是指净化水中污染物所需要的水。由于统计资料中统计的水资源使用量一般只是蓝水的使用量，忽略了绿水和灰水使用量，因此以往的研究实际上测算的是蓝水的利用效率。由于农业生产除了使用统计资料中蓝水之外，还使用了大量的绿水，天然降水量丰富的地区使用的蓝水量很低，并不代表其水资源利用率很高，另外净化农药、化肥残留物所需要的灰水大多数文献也没有考虑，因此测算出来的水资源利用效率与实际结果会存在偏差。对非农产品生产来说，净化污染物也需要消耗水资源，例如净化化工产品所排放的污染物所消耗的水资源，因此测算非农产业的用水效率时也需要考虑灰水的使用情况。为此，本文参考EORA数据库中水足迹数据，将绿水足迹、蓝水足迹和灰水足迹统一纳入水资源利用效率的测算框架，进一步测算世界主要经济体的水资源利用效率。

2 研究方法

2.1 SBM-DEA模型

DEA 模型是使用数学规划方法来评价具有多个输入和多个输出决策单元(DMU)之间相对有效性的一种模型.如果决策单元位于生产可能集的前沿面上，则称为DEA有效（魏权龄，2004［18］）。与经典的DEA模型不同，SBM-DEA模型是非径向、非角度的基于松弛的效率测度模型。其中非径向是指在评价效率时不要求投入或产出同比例变动，非角度是指评价效率时不需要基于投入不变或者产出不变的假定，松弛是指投入冗余和产出不足。另外，经典的DEA模型无法处理非期望产出（本人将灰水作为非期望产出），SBM-DEA模型可以方便地处理非期望产出。参考Tone(2001)［19］、Tone(2004)［20］、Deng 等 (2016)［5］、邓光耀和张忠杰（2019）［1］、邓光耀（2019）［21］、邓光耀（2020）［2］，本文构建的SBM-DEA模型如下：

为了求解以上SBM-DEA模型，需要将公式（1）所示的非线性规划模型转换为以下线性规划模型：

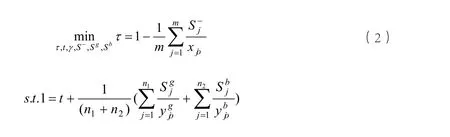
其中，IE称为投入无效率，OE称为产出无效率。另外，可以通过具体某项投入冗余（例如绿水投入冗余）除以该项投入得到具体某项投入的无效率值。类似地，对具体某项期望产出（例如增加值），则直接用期望产出的不足除以该项产出得到具体某项期望产出的无效率值，对具体某项非期望产出（例如灰水足迹），则直接用非期望产出的冗余除以该项产出得到具体某项非期望产出的无效率值。实际上，投入无效率是指各决策单位单元投入冗余的加权平均值；期望产出无效率是指各决策单位单元期望产出的加权平均值；非期望产出无效率是指各决策单位单元非期望产出的加权平均值。本文以世界主要国家的增加值为期望产出，薪酬（也即劳动力投入）、资本消耗以及绿水足迹、蓝水足迹为投入，灰水足迹为非期望产出。

2.2 核密度估计

由于不同年度不同国家的水资源利用效率存在差异，为了分析2006-2015年各国水资源利用效率的变化情况，本文采用核密度估计方法来演进水资源利用效率的动态演进。核密度估计是一种非参数估计方法，它是直方图的推广，本文对世界主要国家水资源效率（投入无效率以及产出无效率）测算结果的概率密度进行估计（Li和Racine等，2007［23］）。核密度估计的具体公式如下：

其中，f (x)是指密度函数，n是指样本个数，h是指带宽，K()是指核函数。本文选用以下公式所示的高斯核函数：

另外，在选择高斯核函数的情况下，最优带宽h*为：

其中，δ=0.7764，s为样本的标准差。

需要说明的是，核密度估计存在边界效应，如果横坐标是有界的（例如水资源利用效率作为横坐标应当在0-1之间），那么在边界处如果纵坐标所对应的密度值不为0，那么会自动扩充横坐标（也即使得水资源利用效率值出现大于1或者小于0的结果），直到纵坐标所对应的密度值平滑过渡到0为止。如果不处理边界效应，会导致水资源利用效率的核密度估计图中可能会出现水资源利用效率值小于0和大于1的情况，因此，本文的核密度估计图中均处理了边界效应。

3 数据来源

本文中数据均来自于EORA数据库Lenzen等，2012［24］；Lenzen等，2013［25］）。其中，各经济体的增加值、薪酬和资本消耗来自于EORA子数据库EORA26，具体为EORA26中世界投入产出表的各国（地区）增加值账户。另外，绿水、蓝水和灰水足迹数据来自于EORA26数据库中的环境核算账户。EORA26包括1990-2015年世界189个国家（地区）26个部门的投入产出表，为了研究方便，本文选取2015年增加值处于前50位的经济体进行研究，另外研究时间范围为2006-2015年①需要说明的是，由于水足迹计算方法较为复杂，EORA数据库最新数据只到2015年。。由于增加值处于前50位的经济体中部分国家（地区）的绿水足迹、蓝水足迹或者灰水足迹值为0，DEA模型不适合处理0值数据，因此本文进一步将这些国家删去，最后保留的国家（地区）数为46个。本文选取的46个国家（地区）的增加值占所有189个国家（地区）增加值的90.29%，因此本文选取的46个国家（地区）可称为世界主要经济体。本文选取的46个主要经济体的名称及代码表1：

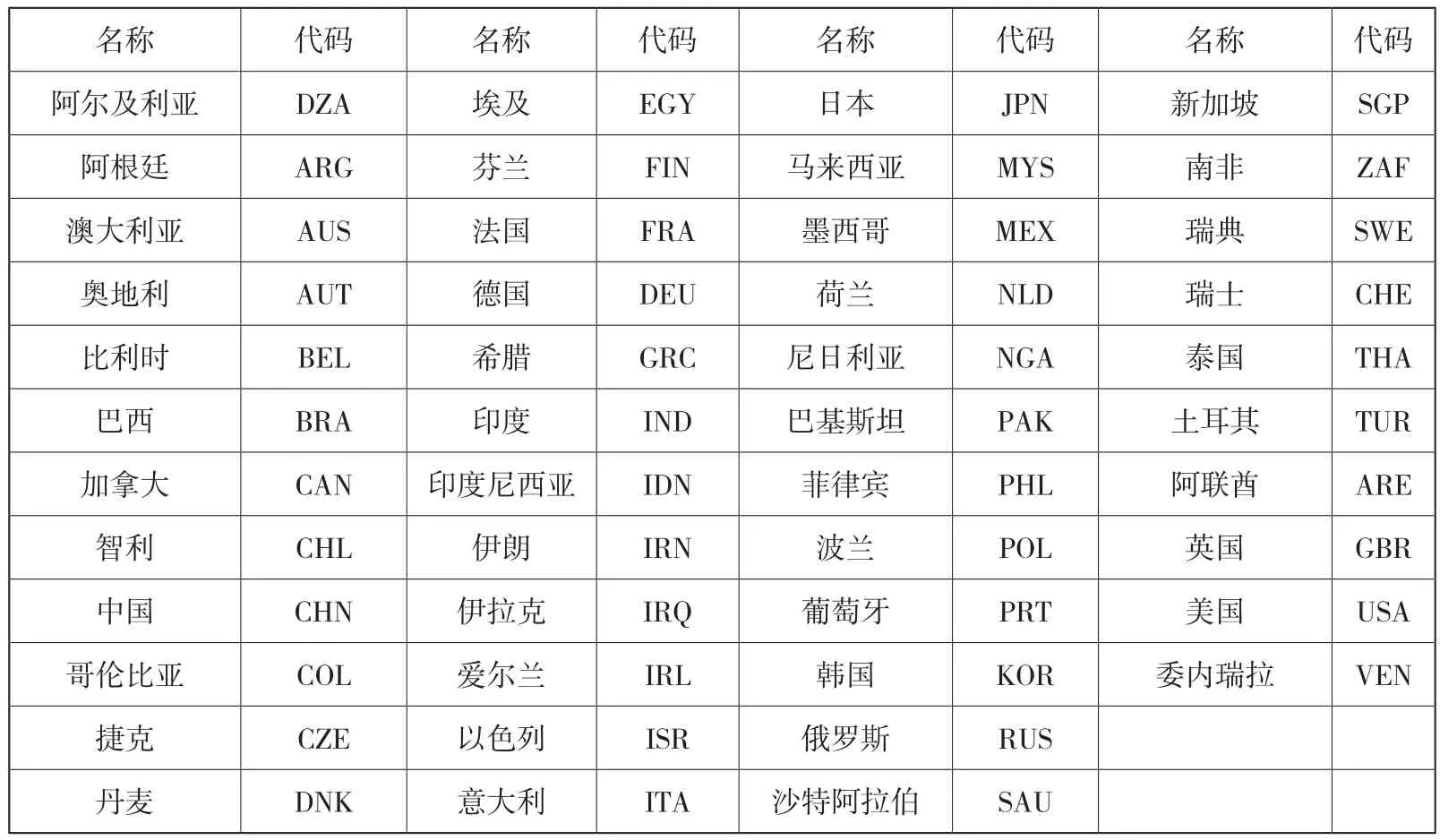
表1 46个主要经济体的名称与代码

4 实证分析

4.1 水资源利用效率的测算结果

本文以每个年度46个世界主要经济体为决策单元，利用公式（1）测算各决策单元的水资源利用效率。2006年和2015年的测算结果如表2所示：

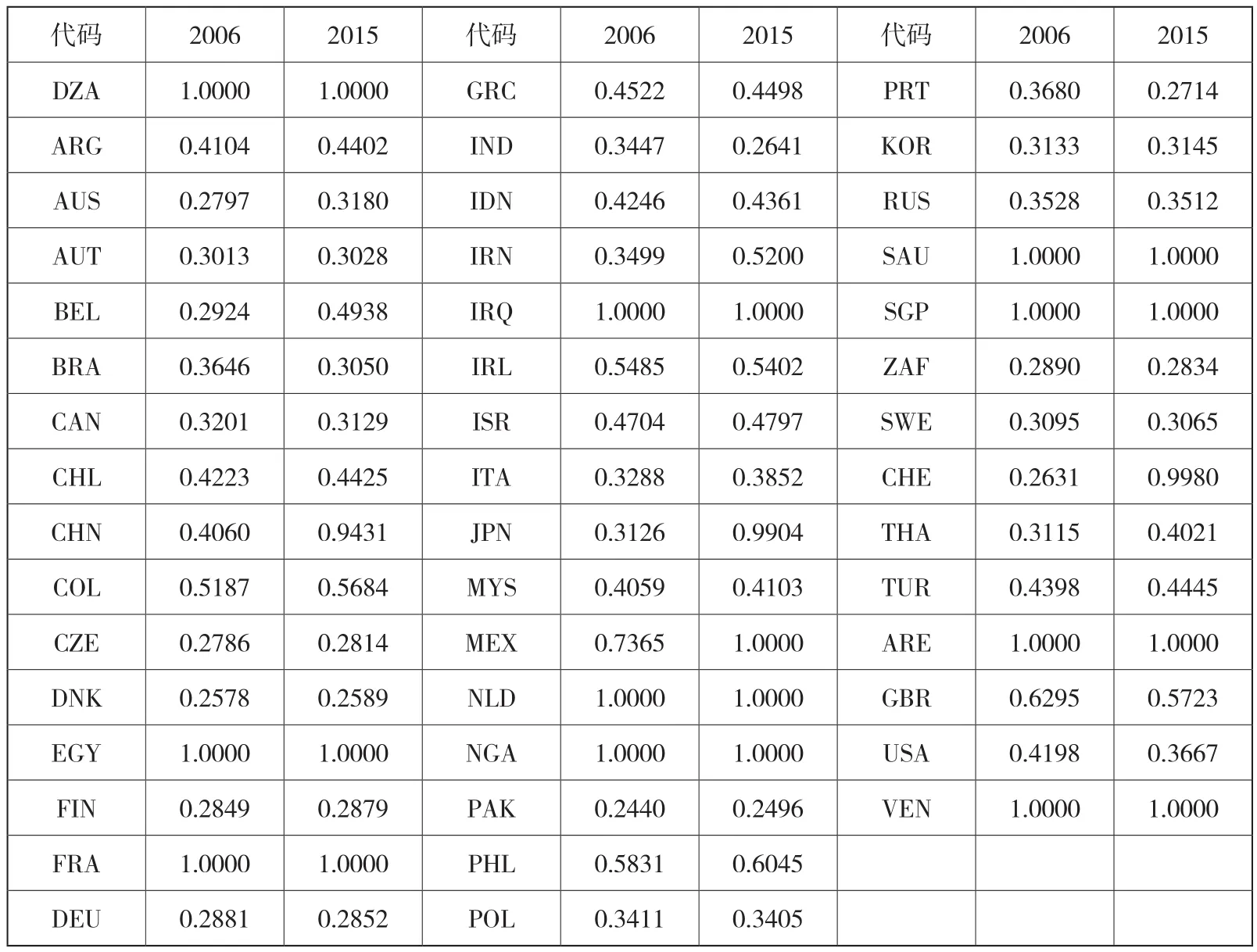
表2 2006年和2015年世界主要经济体的水资源利用效率

从表2可以看到：（1）2006年和2015年均处于前沿面（也即水资源利用效率值等于1.0000）的国家有阿尔及利亚(DZA)、埃及(EGY)、法国(FRA)、伊拉克(IRQ)、荷兰(NLD)、尼日利亚(NGA)、沙特阿拉伯(SAU)、新加坡(SGP)、阿联酋(ARE)、委内瑞拉(VEN)，这些国家大部分是水资源短缺国家。由于水资源短缺，这些国家不得不采取节水措施，提高水资源利用效率。当然水资源丰富的国家也有可能由于采用了节水减排措施，水资源利用效率也较高。另外，2015年墨西哥(MEX)的水资源效率值也等于1。需要说明的是，虽然以色列（ISR）节水技术和水资源利用技术全球领先，也即水资源利用的绝对效率很高，但是这只是考虑水资源一种投入要素的结果，当综合考虑薪酬（也即劳动力投入）、资本、绿水、蓝水以及灰水时，以色列的水资源利用的相对效率并不是最高的，因此在表2中以色列（ISR）2006年和2015年的水资源利用效率值只有0.4704和0.4797。（2）与2006年相比，阿根廷(ARG)、澳大利亚(AUS)、奥地利(AUT)、比利时(BEL)、智利(CHL)、中国(CHN)、哥伦比亚(COL)、捷克(CZE)、丹麦(DNK)、芬兰(FIN)、印度尼西亚(IDN)、伊朗(IRN)、以色列(ISR)、意大利(ITA)、日本(JPN)、马来西亚(MYS)、巴基斯坦(PAK)、菲律宾(PHL)、韩国(KOR)、瑞士(CHE)、泰国(THA)、土耳其(TUR)等国家2015年更接近前沿面，也即水资源利用效率相对提升①本文使用的SBM-DEA模型是静态DEA模型，因此实际上是逐年测算世界46个经济体的水资源利用效率，2015年的前沿面与2006年的前沿面并不一样，也即2015年的参考对象和2006年的参考对象不一样。对同一个国家来说，如果2015年的水资源利用效率的测算值大于2006年的值，指的是相对于2006年该国水资源利用效率水平离2006年的前沿面较远来说，2015年该国的水资源利用效率水平更接近2015年的前沿面，也即本文所说的相对提升。。与2006年相比，巴西(BRA)、加拿大(CAN)、德国(DEU)、希腊(GRC)、印度(IND)、爱尔兰(IRL)、波兰(POL)、葡萄牙(PRT)、俄罗斯(RUS)、南非(ZAF)、瑞典(SWE)、英国(GBR)、美国(USA)等国家2015年距离前沿面更远，也即水资源利用效率相对下降。这些国家水资源利用效率较低的原因可通过后面的投入无效率或者产出无效率来解释。

为了分析2006-2015年世界主要经济体水资源利用效率的变化情况，本文进一步利用核密度估计方法进行研究，为了便于分析，本文选取2006年、2009年、2012年和2015年各主要经济体的水资源利用效率值，具体的核密度估计如图1所示：

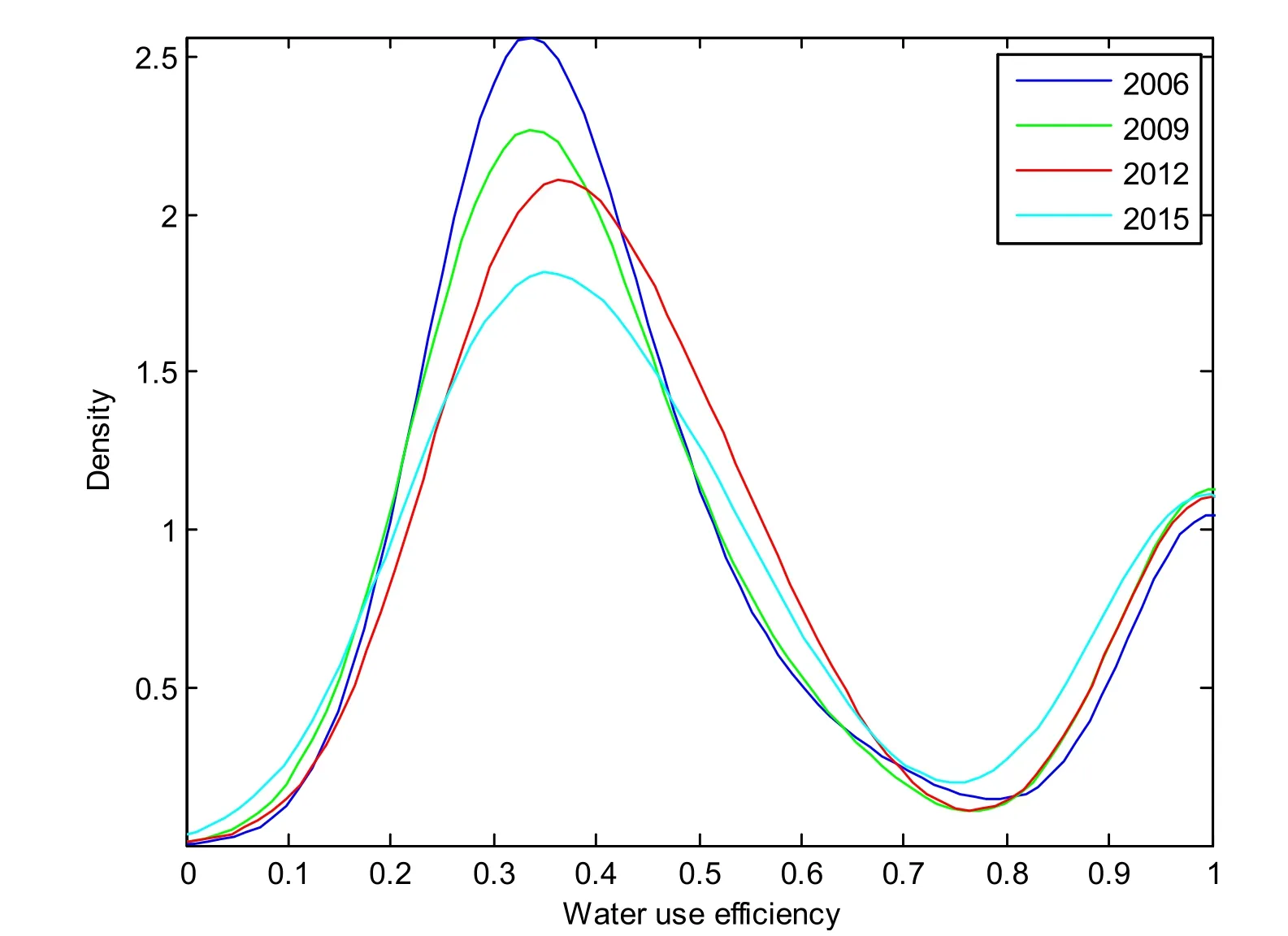
图1 2006年、2009年、2012年和2015年世界主要经济体水资源利用效率的核密度估计

从图1可以看到：（1）2006年、2009年、2012年和2015年世界主要经济体水资源利用效率的核密度函数均呈现双峰分布特征，密度函数的中心所对应的水资源利用效率值在0.4和1附近。这是因为世界主要经济体水资源利用效率集中在0.4和1附近，具体来说，处于DEA前沿面的各国在1附近，未到达DEA有效的各国水资源利用效率的平均值在0.4附近。另外第一个波峰所对应的密度值更大，这是因为水资源利用效率未处于前沿面的样本数更多。（2）从波峰所对应的密度值来看。2006年第一个波峰对应的密度值最高，其次是2009年和2012年，最后是2015年，第二个波峰的情况与此相反。这说明2015年DEA有效或者水资源利用效率值接近1的样本最多。（3）2006年、2009年、2012年和2015年世界主要经济体水资源利用效率的核密度函数每个波峰段均接近对称分布。这说明每个波峰段两边的样本个数大致相等。

4.2 投入无效率和产出无效率

本文以2015年为例，说明46个世界主要经济体投入无效率和产出无效率情况，如表3所示：

从表3可以看到：（1）2015年水资源效率值等于1的国家投入和产出均是有效的，因此各项投入无效率值以及产出无效率值均等于0。（2）在各项投入无效率中，薪酬和资本投入无效率值相对较小，绿水和蓝水投入无效率值相对较大，这是因为生产单位增加值的产品，各国薪酬和资本投入差异较小，但是水资源投入可能差异较大。一般来说，农业生产的绿水和蓝水投入量远高于其他行业，因此农业产值占比较高的国家水资源投入量会远高于工业化国家。从四种投入无效率的平均值来看，巴基斯坦(PAK)、丹麦(DNK)、印度(IND)等国家存在较大的投入无效率。从各项投入无效率来看，印度(IND)、丹麦(DNK)、瑞典(SWE)等国家薪酬无效率值较大，巴西(BRA)、南非(ZAF)、巴基斯坦(PAK)等国家资本无效率值较大，澳大利亚(AUS)、Austria(AUT)、加拿大(CAN)、捷克(CZE)、丹麦(DNK)、芬兰(FIN)、德国(DEU)、波兰(POL)、葡萄牙(PRT)、韩国(KOR)、俄罗斯(RUS)等国家的绿水和蓝水投入无效率值均很高（大于0.9）。（3）从产出无效率来看，非期望产出灰水的无效率值较高，期望产出增加值的无效率值较低。在46个世界主要经济体中，仅有阿根廷(ARG)、澳大利亚(AUS)、比利时(BEL)、瑞士(CHE)、土耳其(TUR)等国家存在增加值无效率。除水资源利用效率等于1的国家之外，其他国家均存在灰水非期望产出无效率。部分国家绿水和蓝水投入无效率值以及灰水非期望产出无效率值均大于0.9，这说明与处于前沿面的国家相比，这些国家不但节水技术相对较低，而且污水处理技术也相对较低。

为了分析2006-2015年世界主要经济体投入无效率和产出无效率的变化情况，本文进一步利用核密度估计方法进行研究，2006年、2009年、2012年和2015年四项投入无效率的平均值以及两项产出无效率的平均值核密度估计如图2和图3所示：

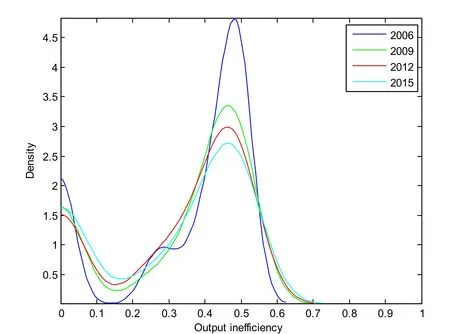
图3 2006年、2009年、2012年和2015年世界主要经济体产出无效率的核密度估计

从图2和图3可以看到：（1）2006年、2009年、2012年和2015年世界主要经济体投入无效率和产出无效率的核密度估计函数均呈现双峰分布特征。第一个波峰所对应的投入无效率或者产出无效率值在0附近，第二个波峰所对应的投入无效率或者产出无效率值在0.4-0.6之间，并且第二个波峰所对应的密度值更高。这是因为部分DEA有效的样本投入无效率或者产出无效率值等于0，0附近的样本个数较多，从而出现第一个波峰；投入无效率和产出无效率的样本集中在0.4-0.6附近，因此出现了第二个波峰；另外投入无效率和产出无效率的样本数比DEA有效的样本数更多，因此第二个波峰所对应的密度值更高。（2）在投入无效率中，与其他年份相比，2012年第一个波峰所对应的密度值最大，2006年第二个波峰所对应的密度值最大。这说明2012年投入有效或者接近有效的样本数最多，2006年接近第二个波峰的投入无效率的样本数最多。（3）在产出无效率中，与其他年份相比，2006年第一个波峰和第二个波峰所对应的密度值最大。这说明2006年产出有效或者接近有效的样本数最多，2006年在产出无效率平均值附近的样本数也最多，也即2006年的样本更集中在波峰附近。

4.3 进一步分析

本文进一步分析水资源利用效率、投入无效率、产出无效率在2006-2015年的年度平均值，如表4所示：

从表4可以看到：（1）在2006-2015年始终位于前沿面（水资源利用效率值等于1）的国家有阿尔及利亚(DZA)、埃及(EGY)、法国(FRA)、伊拉克(IRQ)、荷兰(NLD)、尼日利亚(NGA)、沙特阿拉伯(SAU)、新加坡(SGP)、阿联酋(ARE)、委内瑞拉(VEN)，由于这些国家始终是DEA有效的，因此各项投入无效率和产出无效率值均为0。（2）从四项投入无效率的平均值来看，巴基斯坦(PAK)、捷克(CZE)、德国(DEU)等国家在2006-2015年存在较大的投入冗余。另外，大部分国家的投入无效率中，薪酬和资本投入无效率值相对较小，绿水和蓝水投入无效率相对较大。（3）从两项产出无效率的平均值来看，捷克(CZE)、德国(DEU)、波兰(POL)等国家在存在较大的产出不足。另外，大部分国家主要是非期望产出（灰水）无效率。（4）澳大利亚(AUS)、加拿大(CAN)、捷克(CZE)、丹麦(DNK)、芬兰(FIN)、德国(DEU)、意大利(ITA)、波兰(POL)、韩国(KOR)等国家在2006-2015年水资源利用效率较低（低于0.35），绿水和蓝水的投入以及非期望产出灰水的无效率值均在0.9以上。

需要指出的是，由于影响世界主要经济体水资源利用效率各变量数据的缺乏，本文未对水资源利用效率的影响因素进行回归分析。不过，已有文献在研究水资源效率的影响因素时，采用的变量也不一样。另外，也有部分文献只测算水资源利用效率，未考虑水资源利用效率的影响因素［26］-［27］。因此，本文未对水资源利用效率的影响因素进行回归分析虽然存在一定的不足，但是在水足迹视角下，对水资源利用效率进行国家间比较仍是可取的。

5 结论和启示

5.1 结论

本文利用EORA数据库中绿水、蓝水和灰水足迹相关数据，测算了2006-2015年46个世界主要经济体的水资源利用效率，研究结果发现：（1）在2006-2015年始终位于前沿面（水资源利用效率值等于1）的国家有阿尔及利亚(DZA)、埃及(EGY)、法国(FRA)、伊拉克(IRQ)、荷兰(NLD)、尼日利亚(NGA)、沙特阿拉伯(SAU)、新加坡(SGP)、阿联酋(ARE)、委内瑞拉(VEN)。（2）澳大利亚(AUS)、加拿大(CAN)、捷克(CZE)、丹麦(DNK)、芬兰(FIN)、德国(DEU)、意大利(ITA)、波兰(POL)、韩国(KOR)等国家在2006-2015年水资源利用效率较低（低于0.35），绿水和蓝水的投入以及非期望产出灰水的无效率值均在0.9以上。

5.2 启示

根据以上研究结果，可得以下政策启示：（1）由于世界主要经济体之间水资源利用效率、投入无效率和产出无效率方面存在较大差异，因此各国政府需要因地制宜，制定与当地经济发展状况、自然条件等相适宜的节水灌溉等提升水资源利用效率方面的政策，以及污水治理等处理非期望产出方面的政策。（2）水资源利用效率较低的国家需要向水资源利用效率较高的国家学习节水技术和污水治理方面的先进经验，切实提高全要素视角下的水资源利用效率。