维数约化的弱耦合KP-Boussinesq方程的lump解和有理解

刘 袁,汪一航

（宁波大学 数学与统计学院,浙江 宁波 315211）

非线性演化方程描述了非线性现象,具有广泛的应用.非线性演化方程的精确解在非线性科学中起着至关重要的作用[1-2].lump 解是一种特殊的有理解,它在空间的各个方向都是局域的[3-4].基于构造平方函数[5-7]和长波极限的方法[8-10],诸多方程都被发现存在lump 解.

(3+1)维的广义KP-Boussinesq 方程[11]为

相当于把utt的项添加到广义KP 方程中,u=u(x,y,z,t)是可微函数.通过变量变换

可得式(1)的Hirota 双线性形式,即

式中:f=f(x,y,z,t)为实辅助函数;D为Hirota双线性微分算子.利用极大交换子代数中取值的Zm-KP 方程族结构[12-13],得到弱耦合KP-Boussinesq方程:

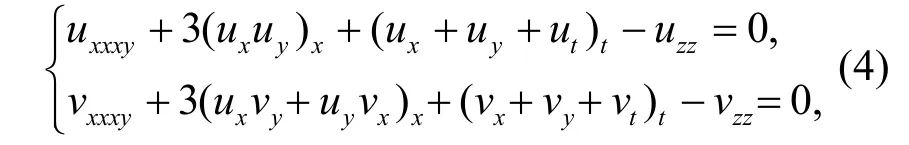
式中,v=v(x,y,z,t)是可微函数.

1 lump 解和有理解

1.1 lump 解

对于z=y的情况,式(4)可简化为

A和B为对称矩阵,A和B的元素及c1、c2均为实变量.

将式(9)代入式(7),求解方程得到各参数的约束方程

为保证解u为lump 解,矩阵A和参数c1必须满足以下约束:

(i)矩阵A是一个半正定矩阵;

条件(i)和(ii)保证f是一个恒大于0 的函数.条件(iii)保证f在任意时刻只有一个最小值.

在式(12)中有自由参数a22、a23、a33和c1.对各参数取值如下:

图1 t=0 时lump 解u 的特征

图2 t=0 时lump 解v 的特征

1.2 有理解

本节主要研究方程(4)的另一种有理解,它表现出不同于lump 解的性质.

将式(9)代入式(7)可解得如下约束方程:

上式包含3 个自由参数b22、b23和b33,令参数值为

辅助函数g的解析表达式为

那么在变量变换(6)下可得vr:

上述vr为方程(5)的有理解,图3 所示为有理解vr在不同时刻的动力演化.

图3 有理解 v r在不同t 下的动力演化

分析有理解vr,其表现出不同于lump 解的性质.首先,vr是奇函数,即满足vr(x,y,t)+vr(-x,-y,-t)=0.如果能计算出波峰在t﹥ 0时的轨迹,那么可知任何t下的波峰位置.vr的偏导数反映了解的极值的性质,通过计算vr,x=0和vr,y=0不能直接解出有理解的极值.为了分析解的波峰和轨迹变化,需要采用数值方法来研究其性质.

表1 描述了t取不同值时有理解vr的波峰变化,其中h为峰值高度,|vr,x|和|vr,y|的数值越小,计算的波峰位置越精确.从图3 可以看出,随着时间的增加,波峰高度逐渐减小.当t﹤ 0时,波峰高度为正;当t﹥ 0时,波峰高度为负.

根据前面的描述,对表1 中的数据进行非线性拟合.

表1 有理解 vr 的波峰位置和高度

对于t﹥ 0,波峰的运动轨迹近似符合下式:

根据奇函数的性质,在t﹤ 0处波峰的轨迹为

波峰的高度h为

由式(23)可知,随着时间的增加,波峰的运动过程近似为匀速线性运动.此外,任何单位时间所产生的高度变化值大约为2.为验证式(21)和式(22)能否准确表示出波峰的位置和高度,另取不同的t值,可得相应的波峰坐标和高度,见表2.其中|vr,x|和|vr,y|略有增加,这是因为当|t|越大,波峰越尖锐,高度h的误差略有增加,但这仍是有效计算出波峰高度的一种方法.

表2 有理解 vr 的估计

2 结语

在本研究中,利用Zm-KP 方程族构造了一个新的弱耦合广义KP-Boussinesq 方程.基于Hirota双线性方法和符号计算研究了其维数约化情形的有理解问题.通过假设半正定的对称矩阵形式的辅助函数,限制参数之间的关系,得到了lump 解和有理解,并讨论了lump 解的动力学性质.然后发现了一种不同于lump 解的有理解,并分析了其动力学性质.由数值分析给出了有理解的波高和极值点的运动轨迹,并通过相应的图表来说明其运动规律.希望本文所描述的新结果能够对其他非线性模型的应用有所帮助.