并联隔振系统刚度归一化及固有频率的计算与验证*

（中国船舶集团第七二二研究所武汉迈力特通信有限公司 武汉 430205）

1 引言

动力学的经典通用运动方程为［3］

式中：［M］是质量矩阵［4］、［C］是阻尼矩阵［4］、［K］是刚度矩阵［6］、δ是位移、F是激励力。F是时间t的函数。

不同的分析类型对应不同形式的求解方程：1）对于模态分析时，则F（t）=0，［C］被忽略；2）对于谐响应分析，F（t）与δ（t）都假设为谐函数，例如正弦振动；3）对于瞬态动力学分析，上述方程保持其完整性不变等。

因此，单自由度方向正弦振动的微分方程可简化成如下方程：

正弦运动位移：δ（t）=Xsin（ωt+φ）。

式中：ω为角频率，ω=2πf（rad/s）；f为周频率（Hz），即单位时间内振动的次数；X为位移峰值（mm），即振幅；φ为初始相位角（rad）；t为时间（s）。

解上述简化方程，得：

因此，对于并联隔振系统，明确了系统刚度和载荷质量后，即可得到隔振系统的振动频率（即固有频率）。

材料的刚度是由使其产生单位变形所需的外力值来衡量的。各向同性材料的刚度取决于它的弹性模量E和剪切模量G，还与其几何形状、边界条件等因素有关。

等效刚度：材料、外形及几何尺寸固定的物体，其自然频率（又称固有频率）是固定不变的，因此使用线性等刚度或非线性变刚度隔振器时，在固定载荷质量作用下，其固有频率是固定不变的。为了简化计算，可先简化计算用的数学模型。实际研究过程中，将刚度做归一化处理［7］，得到一个固定的刚度值。这个固定的刚度值，就是等效刚度［8］。

下图表示由两个弹性系统，归一化拟合成一个弹性系统的过程［8］。

图1（a）表示由刚度分别为K1和K2的组成的弹性系统，在矢量力作用下，产生位移。根据胡克定律，得到以下等式。

图1 并联刚度转化过程

图1（b），在相同矢量力作用下，也产生相同位移。以上同理，可得如下等式。

图1 某设备振动扫频结果

对比等式（1）、（2），于是就可得出：K=K1+K2，K就是K1+K2弹性系统的等效刚度。

依次类推，多个隔振器并联使用时，单个隔振器的刚度分别是 K1、K2、K3，…，则并联系统的等效刚度：

所以并联使用弹性系统时，系统的刚度系数K是各个隔振器的刚度系数Ki的算术之和。实际使用中，各个隔振器的算术符号完全相同，要么全为“+”，要么全为“-”，因此，并联后隔振系统的刚度，都会强于单个隔振器的刚度，即

由于小阻尼对振动周期略有影响［8］，所以此处可忽略阻尼的影响，隔振系统的振动频率可近似计算如下：

式中：f为隔振系统的振动频率，即隔振系统的固有频率；|k|为隔振系统的刚度系数，即隔振系统的等效刚度；m为隔振系统所承受载荷的质量。

由式（5）可知，当知晓并联隔振系统的等效刚度|k|与隔振系统载荷的质量m后，就可计算出无阻尼状态下，并联隔振器系统的单自由度方向的振动频率，且f与|k|正相关，也就是说，在相同载荷质量m的作用下，并联后隔振系统的振动频率，将朝频率f轴的正方向移动，即并联后隔振系统的固有频率，将高于单个隔振器的固有频率。

例如，已知在载荷质量m作用下，刚度是Kj的隔振器，其固有频率是f1j。

当四个刚度系数是Kj的相同隔振器并联使用时，根据式（3）可计算出隔振系统的等效刚度系数是 4Kj。根据前面式（5）中 f与|k|的关系，并联后隔振系统的固有频率将增加到2f1j。计算过程如下。

并联隔振系统等效刚度|k|=K1+K2+K3+K4=Kj+Kj+Kj+Kj=4Kj。

单个隔振器使用时，固有频率为

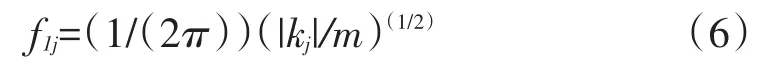
四个隔振器并联使用时，固有频率为

解由式（6）、（7）组成的方程组，得

以上描述的是等刚度隔振器组成的隔振系统的等效刚度归一化拟合方法和固有频率计算方法。

实际工程应用中，我们也经常会遇到变刚度隔振器组成的隔振系统［9～11］。我们长期的振动试验得到的试验结果表明，类似不锈钢钢丝绳隔振器，属变阻尼变刚度型隔振器，在单一轴方向振动时［12］，用前面的等刚度归一化方法计算得出的等效刚度及固有频率，与试验结果接近度很高。

因此，对并联变刚度隔振系统的等效刚度归一化处理，也可参照此方法，从而可大大减少设计建模工作量和计算工作量，以提高设计效率。

2 实例验证

举一具体实例，来对刚度归一化的拟合算法及频率计算数学模型进行验证。

某挂装安装式设备的隔振系统，选用了两个型号为GH-40B的不锈钢钢丝绳隔振器，该隔振器平坐安装时的额定载荷能力是4kg、侧挂安装时的载荷能力是1.8kg。

隔振器特性见表1。

表1 隔振器特性表

隔振系统承载的设备质量是3.2kg。隔振器的额定承载能力之和是8kg，与设备重量之比是8÷3.2=2.5（倍）。

查表1得到厂家给出的隔振器的特征数据如下。

GH-40B隔振器侧挂额定载荷1.8kg，垂直于挂装安装面（即平坐方向）振动时的固有频率范围是9Hz～12Hz。根据隔振器厂家的实测结果，并根据固有频率、刚度系数与质量之间的数学关系，以及1.8kg额定载荷对应的隔振器的固有频率是12Hz，对应的方程式如下：

定义并联使用两个GH-40B组成的隔振系统的固有频率为f21，并联后，系统等效刚度是2K，隔振系统挂装承载的载荷质量3.2kg时，则对应的方程式如下：

解由式（6）、（7）组成的方程组，得

图2是振动试验时振动扫频结果，共振点在12.67Hz，与计算出的12.73Hz固有频率比较接近。考虑测量误差，基本可判定两者结果是相同的。

3 仿真验证

3.1 不锈钢隔振器

某不锈钢材质隔振器的形态如图3所示。

图3 某隔振器三维状态图

下面，我们将在Y轴方向，用ANSYS Workbench有限元仿真软件，在相同载荷质量m作用下，分别仿真分析单个隔振器、两个隔振器、四个隔振器组成的隔振系统的固有频率，看看仿真结果是否固有频率计算结果一致。

定义用fij表示隔振系统的固有频率，其中i表示并联隔振器的数量，j表示振动阶次，如f21表示由两个隔振器组成的隔振系统的第1阶固有频率。

3.2 单隔振器隔振系统

首先声明一下，在如车、船、飞机等环境下，不会出现如下图所示的单隔振器系统，但在理想的单轴方向，将单隔振器系统作为一种研究方法，以及作为研究对象是可行的，单隔振器系统是我们研究及参照基础。

载荷质量m，单隔振器组成的隔振系统三维形态如图4所示。

图4 单隔振器隔振系统三维状态图

经仿真，前六阶固有频率及振型见表2。

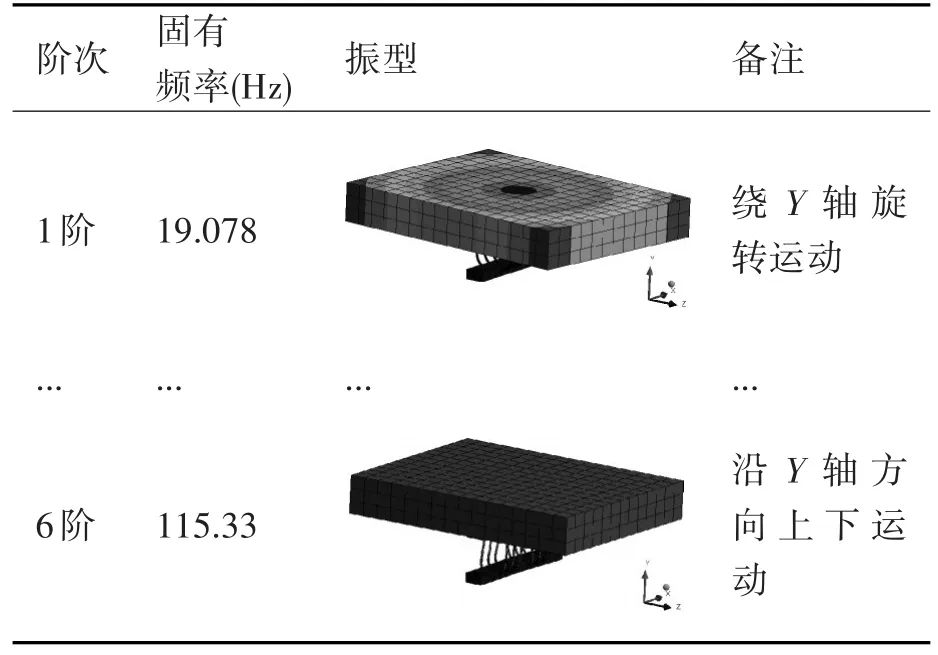
表2 单隔振器系统固有频率及振型

对比表2中的各阶振型，可看出，只有第六阶振型是沿Y轴方向运动的，第六阶的固有频率是f16=115.33Hz。

3.3 双隔振器隔振系统

载荷质量m，双隔振器组成的隔振系统三维形态如图5所示。

图5 双隔振器隔振系统三维状态图

经仿真，前六阶固有频率及振型见表3。

表3 双隔振器系统固有频率及振型

对比表3中的各阶振型，可看出，只有第五阶振型是沿Y轴方向运动的，第五阶的固有频率是f25=160.32Hz。

3.4 四隔振器隔振系统

载荷质量m，四隔振器组成的隔振系统三维形态如图3所示。

经仿真，前六阶固有频率及振型见表4。

表4 四隔振器系统固有频率及振型

对比表4中的各阶振型，可看出，只有第六阶振型是沿Y轴方向运动的，第六阶的固有频率是f46=220.2Hz。

3.5 结果对比分析

我们将根据前文提供的刚度拟合及固有频率计算方法，计算出三种隔振系统在Y轴方向振动时的固有频率，并与仿真结果进行对比，对比结果见表5。

表5 隔振系统固有频率计算与仿真结果对比表（Hz）

仿真及计算，都存在一定的误差，忽略这些误差，可判定仿真结果与计算结果是相同的。

图6 四隔振器隔振系统三维状态图

4 结语

通过实物振动试验扫频验证及仿真结果验证，证明了本文提供的并联隔振系统的刚度归一化拟合技术及并联隔振系统固有频率的计算方法是正确的，对设计并联隔振系统具有较好的指导意义。