基于脉内特征的灵巧类干扰分组识别*

（海军航空大学信息融合研究所 烟台 264001）

1 引言

干扰识别的意义在于感知干扰环境，为雷达提供更多的先验信息，使雷达更有针对性的对干扰进行及时抑制。由DRFM产生、专门针对相参雷达的的灵巧类干扰，由于能够获得全部或者部分脉压处理增益，影响真实回波信号的正常检测，兼有欺骗和压制特点，威胁性大。文献［1～8］从信号特性角度入手，在时域、频域、时频域、小波域和统计域等变换域内挖掘干扰信号与目标信号差异明显的特征信息，达到回波、欺骗式干扰样式识别目的。文献［9］提出一种区分卷积灵巧噪声干扰和目标回波多维特征处理识别方法，通过提取目标和干扰信号的包络起伏参数、相位门限概率、盒维数、近似熵，构建特征向量，使用SVM分类器进行检测识别。但是现有文献针对灵巧类干扰的分类识别研究较少，本文针对五种典型的灵巧类干扰样式，分别是卷积、乘积灵巧噪声干扰，间歇采样转发、C&I干扰和SMSP干扰，根据不同样式工作原理的差异，采取一级分组判断、二级分类识别的处理流程，通过提取出回波和各类干扰信号的细微差异，逐级进行识别判断。仿真结果验证了本文算法的有效性和可行性。

2 目标与典型灵巧类干扰分析

2.1 目标与典型灵巧类干扰模型

假设目标存在干扰条件下，雷达目标检测模型为

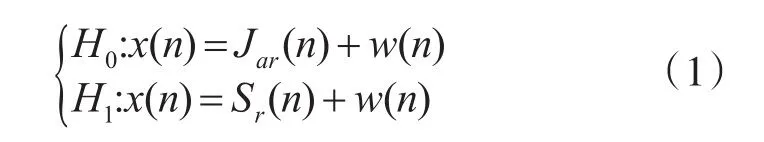
式中，x(n)为接收到的信号，Jar(n)为干扰信号，Sr(n)为回波信号，w(n)为背景噪声。出现H0时，表示检测到干扰；出现H1时，表示检测到回波。

回波信号为线性调频信号，其数学模型：

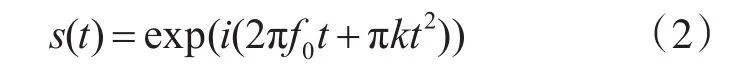
式中，s(t)为发射信号，f0为中频频率，k为发射信号调频斜率，t0为目标距离相对发射信号的延时，fd为目标多普勒频率。

常见的灵巧类干扰主要有卷积灵巧噪声干扰、乘积灵巧噪声干扰、间歇采样转发干扰、SMSP干扰，其干扰原理不再陈述，这里参考相关文献［14～15］，给出其部分数学模型。

卷积灵巧噪声干扰数学模型：

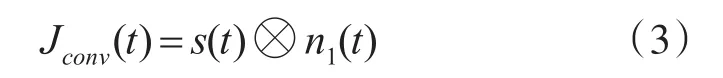
式中，n1(t)为视频卷积噪声，服从高斯分布。

间歇采样转发干扰数学模型：

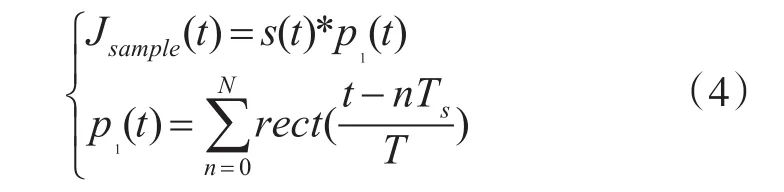
式中，p1(t)为矩形采样函数，T矩形脉冲宽度，Ts为采样周期，N为采样脉冲个数。

频谱弥散干扰SMSP数学模型：

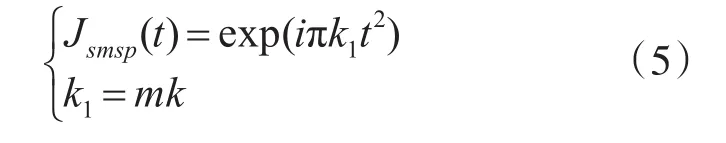
式中，k1为SMSP干扰调频斜率，k为雷达发射信号调频斜率，m为正整数。

2.2 特征提取与选择

1）双正交Fourier变换

双正交Fourier变换由文献［10］提出，采用双正交函数将信号展开，得到调频斜率密度谱，简称斜率谱。对于单个LFM信号，其斜率谱表现为相应的冲激函数，而具有不同调频斜率的LFM信号彼此正交，特别适合分析含有多个LFM成分的信号。

2）频谱熵（pentropy）

信号的频谱熵SE借鉴信息论中的信息熵，用于度量信号的频谱分布，SE将信号在频谱中的归一化功率分布视为概率分布，并计算其香农熵。SE常用于故障检测和诊断中的特征提取，也广泛应用于语音识别和生物医学信号处理［11～13］。由于干扰信号对截获的雷达发射信号调制方式不同，其频谱复杂性也明显不同，因此这一特征参数能够给出识别回波和不同干扰信号的有效信息。

3）互相关系数（corrcoef）

互相关系数是互相关函数的归一化处理，用以度量两个信号的相关程度，若互相关系数越接近1，表示两个信号越相似；反之，互相关系数越接近0，表示两个信号的差异就越大。排除回波噪声外，回波与发射信号的相似程度最高，因此互相关系数最大；而间歇采样转发干扰信号是对发射信号的分段采样，其互相关系数要低于回波信号。因此互相关系数可以作为识别回波与间歇采样转发干扰信号的特征因子。

4）范数熵（Norm Entropy，NoEn）

“熵理论等价于一个条件概率，而不只是一种非线性动态参数，因此，熵理论可以在同时包含随机信号与确定性信号的混合信号中使用”［12～13］。BoekeeD E等人在R范数度量的基础上提出了范数熵的概念。

5）带宽功率比（powerratio）

对于卷积灵巧噪声干扰，LFM可以看作通带为[f0-B/2，f0+B/2]的带通滤波器，其能量主要集中于带宽B内，而乘积灵巧噪声干扰为回波与视频噪声的乘积，其能量随机分布于整个频率范围内，因此带宽功率比特别适合区分这两类干扰信号。

6）小波变换高频分量能量比（wdpowratio）

参考文献［5］中的定义，对接收信号进行一维小波变换，定义M阶小波变换细节分量能量占比：

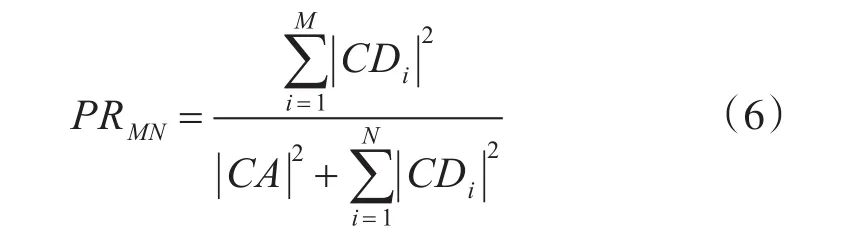
式中，N为小波分解的阶数，M为细节分量的阶数，CDi为第i阶细节分量系数，CA为近似分量系数。

3 目标与典型灵巧类干扰识别流程

为有效识别目标、五种干扰样式共六种信号形式，这里采取“二级分类识别”方法，步骤如图1所示。

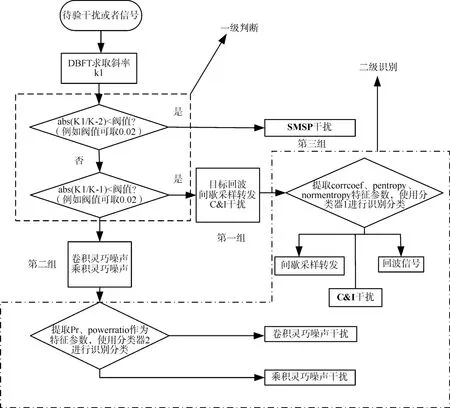
图1 联合识别处理流程

第一步：对接收信号进行双正交Fourier变换，分析斜率谱，提取峰值斜率，与阀值进行比较，将六种信号分成三组：

第一组，回波、间歇采样转发和CI干扰信号。

第二组，卷积、乘积灵巧噪声信号。

第三组，SMSP干扰信号。

第二步：选取相关系数、频谱熵和范数熵作为第一组信号的特征因子，提取特征参数，构造待检测样本，投入训练好的分类器1，完成三种信号的识别；选取带宽功率比、小波变换高频分量能量比作为第二组信号的特征因子，提取特征参数，构造待检测样本，投入训练好的分类器2，完成卷积和乘积灵巧噪声干扰信号的识别。

4 仿真结果与分析

参数设置：设SNR为0dB，JNR为-20:1:20(dB)，雷达发射LFM基带信号时宽为20μs，带宽为20MHz，LFM调频斜率为1000GHz/s，采样频率为80MHz；参与卷积、乘积调制的视频噪声时宽均为20μs，SMSP干扰调频斜率为2000GHz。

本文针对六种信号（回波和五种干扰）利用MonteCarlo实验在不同干噪比下各产生200个样本（JNR 自-20dB～20dB，间隔5dB），每种信号共计1800个样本。不同干噪比随机取出回波、间歇采样转发干扰和CI干扰各100个样本（剩余的100个样本用于测试），共计2700个样本训练分类器1；不同干噪比随机取出卷积、乘积灵巧噪声干扰各100个样本（剩余的100个样本用于测试），共计1800个样本训练分类器2。按照图1的处理流程，对六种信号进行分类识别。

1）一级分组识别情况

图2可以看出，JNR≥-5dB情况下，各组识别率均超过了90%，其中第三组识别最高，达到了100%；第一组在JNR≥-0dB情况下，识别率接近100%；第二组（卷积和乘积灵巧噪声干扰）峰值点对应斜率值存在噪声特点，且与干噪比无关，因此第二组样本存在误分至其他组的情况（即所检测斜率谱峰值点对应的调频斜率约等于雷达发射信号的调频斜率或SMSP干扰的调频斜率），但误分率≤7%，处于可以接受范围。

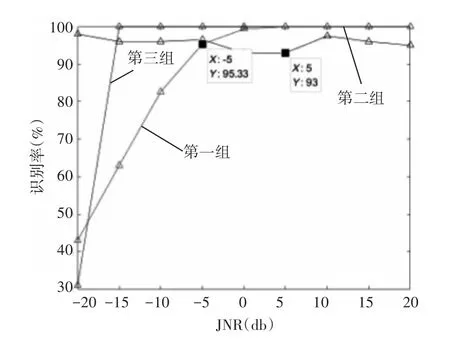
图2 一级识别概率

2）二级分类识别情况

图3、图4可以看出，所选分类器较好地完成了第一组、第二组内部信号分离。第一组三种信号识别中，JNR≥-10db情况下，回波、间歇采样转发干扰识别率达到了100%，而CI干扰在JNR≥-5dB可以达到98%；第二组二种信号中，JNR≥-5dB，信号识别率达到了100%。相比第一组信号识别，卷积和乘积灵巧噪声干扰识别率受干噪比影响较大。

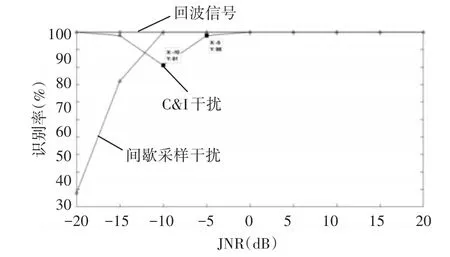
图3 二级识别概率（第一组）

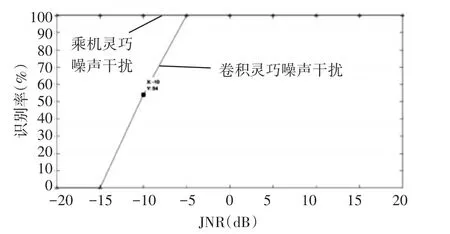
图4 第二级识别概率（第二组）

3）总体识别情况

由图5和表1可以看出，本文所提算法较好地识别了回波和五种干扰信号，其中回波、间歇采样转发干扰、SMSP干扰在JNR≥-9dB情况下，识别率达到了100%；JNR≥-12dB情况下卷积和乘积灵巧噪声干扰识别率超过了90%；CI干扰识别率最低，仅在JNR≥-6dB情况下，识别率才超过90%。

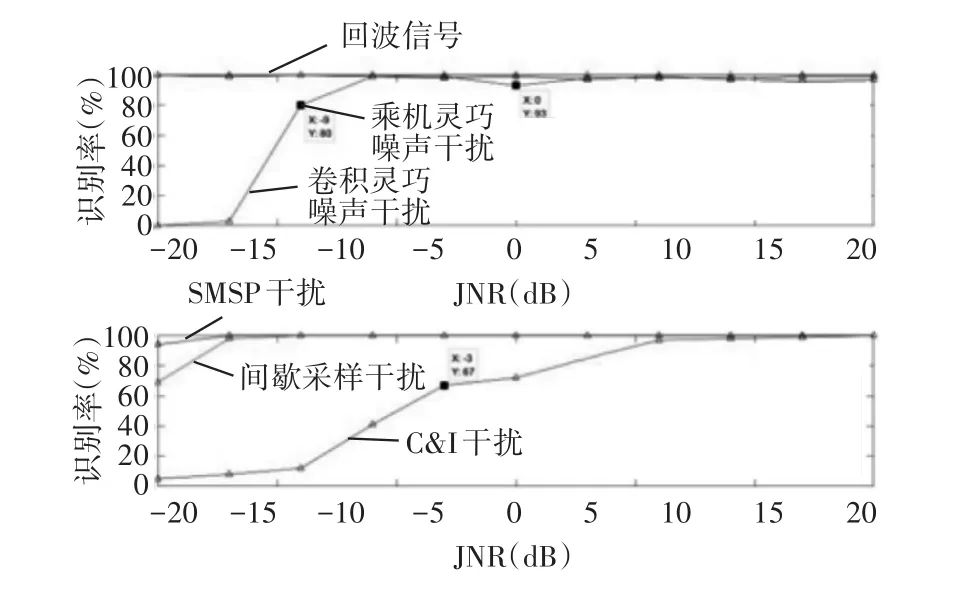
图5 总体识别情况

表1 总体识别情况（%）

5 结语

基于DRFM的灵巧类干扰由于可以获得脉压处理增益，且在检测端产生大量的虚假目标，影响雷达正常检测。本文针对五种典型的灵巧类干扰信号，建立信号数学模型，选取调频斜率、互相关系数、带宽功率比等特征参数，采取二级识别的方法，对回波及干扰信号进行分组识别。相比传统的“一级分类识别”，本文提出的“二级分类识别”方法覆盖干扰类型更广，并充分利用了雷达先验信息。仿真结果验证了该方法的有效性。由于算法对CI干扰识别率较低，下步将针对上述问题，建立更加贴近实际的数学模型，探索更为灵活有效的识别处理方法。