基于遗传算法的贝叶斯网络模型测试配置方法*

（海军航空大学 烟台 264000）

1 引言

装备结构日趋复杂，对故障检测与隔离提出了更高的要求，因而测试性作为装备系统的固有属性，受到越来越多的关注。测试性是描述系统健康状况可监控、可测试的一种设计特性；测试性模型是为设计、分析、评估产品测试性而建立的模型［1］。一个好的测试性模型不仅有助于装备测试性设计开发，对于装备使用周期的维护保养与测试、故障隔离也具有重要的意义。贝叶斯网络测试性模型相比于一般的相关模型［2］，加强了对不确定信息的处理能力，具备更强的推理更新能力，可以更充分地利用已有信息，使得模型更加贴近现实。可针对初步建立的模型开展测试配置，但大型系统故障模式多，结构复杂，现实要求用最少的测点与测试项目，满足既定要求。人工完成测试配置是一项非常繁重的工作，工作量大且重复性工作多，因此针对以上问题，采用针对贝叶斯网络模型的遗传算法来解决问题。

2 贝叶斯网络测试性模型

贝叶斯网络是建立在贝叶斯理论方法基础上，表示变量之间连接概率的图形化模型［3］。贝叶斯理论可综合利用先验信息与样本知识对参数进行估计，因而贝叶斯网络具有良好的学习能力，基于贝叶斯网络的测试性模型可在试验、使用过程中，根据相关数据，不断学习，更新结构与参数，使得测试性模型越来越贴合实际。同时贝叶斯网络具有强大的证据处理能力，可以根据故障表征出的各种信号，迅速做出判断，对故障进行隔离。

贝叶斯网络模型可根据专家经验知识直接建立，也可通过试验、使用、模拟仿真等途径获取的故障测试数据进行学习，从而建立。其结构主要由三部分组成。

节点集X：代表随机变量，在此应用中可以表示故障模式、测试、装备组件等。

有向边集E：代表节点间的相互关系，通过专家知识建立，也可通过网络结构学习获得。

条件概率表CPT：表示该节点与其双亲的依赖关系，这里主要表示故障与故障、故障与测试之间的相关关系。

建立的测试性模型如图1所示。

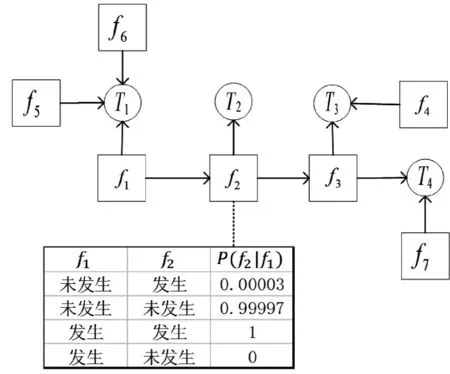
图1 贝叶斯网络测试性模型示意图

针对贝叶斯网络的FDR、FIR计算方法。

贝叶斯网络模型可以通过簇树与连接树等方法进行精确推理与证据处理。因此可以计算出每个测试对于各个模块单元的故障检测率、虚警率、漏检率等信息。单故障模式fi的被检测概率可以通过概率加法公式求得：

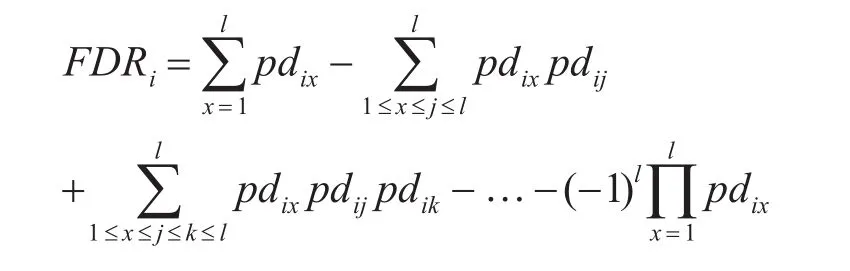
pdix表示通过贝叶斯网络处理证据推理出的测试ti对故障fi的检测率。

这里认为测试对于某故障的故障检测率超过70%，即对该故障具有故障检测能力。

系统的故障检测率为

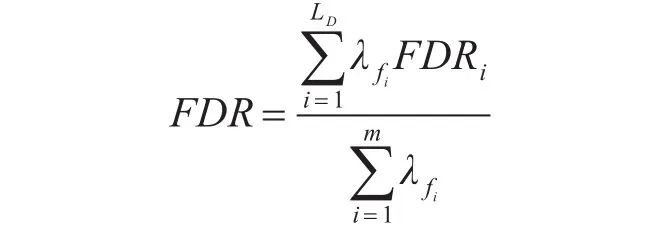
LD表示能检测出的故障数量，m为总的故障数量。

故障隔离率通过下式计算：

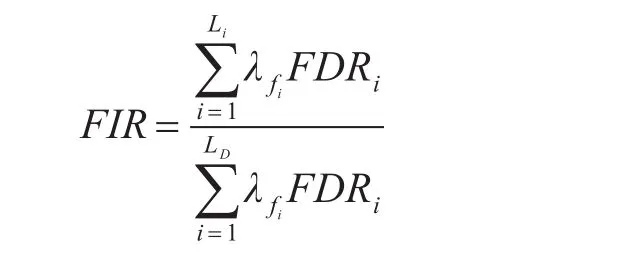
Li表示能达到故障隔离度要求的故障数量。

3 遗传算法

遗传算法是一种新发展起来的优化算法，是基于自然选择和基因遗传学原理的搜索算法［4］。随着算法的迭代运行，过程如生物进化一般，好的特性流传下来，不适应的特性被淘汰。新一代比上一代更能适合环境，整个群体向好的方向发展。由于遗传算法存在变异算子，因此遗传算法可以解决陷入局部最优化的问题。

遗传算法中的基本概念如下。

染色体：遗传因子的集合。在遗传算法中，是一维串结构数据。

遗传因子：又称基因，是控制生物性状的遗传物质的基本单位。

遗传子座：染色体上遗传因子的位置，各个位置决定了遗传什么样的信息。

表现型：由染色体决定性状的外部表现。

个体：染色体带有特征的实体。

群体：个体的集合。

适应度：各个个体对环境的适应程度。

选择：以一定概率从群体中选取若干对个体的操作称为选择。

交叉：两个染色体部分片段互换的操作，又称重组。

变异：让遗传因子以一定概率变化的操作称为变异。

编码：从表现型到遗传子型的映射。

解码：从遗传子型到表现型的映射。

4 基于遗传算法的测试配置

染色体编码：

遗传子座数量设置为测试性模型中所有可能设置测试的位置数量，采用二进制编码方式进行编码，二进制1-0表示其所对应的位置是否布置测试。

染色体初始化：

采用随机方式对染色体进行初始化。

染色体适应度函数的确定：

为将故障检测率与故障隔离率确定在要求标准之上，设置适应度评价函数为分段函数。表达式为

c(ti) 为测试ti的成本，为算法采纳的测试，n为最多可布置的测试数量，m为选取的测试数量。

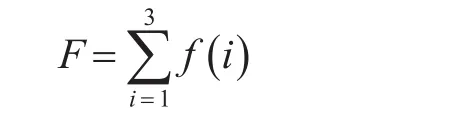
染色体解码：

遗传运算时，群体平均适应度会提高，达到规定迭代次数或平均适应度时停止计算，对染色体进行解码，得到测试配置方案。

5 实例分析

根据仿真数据与专家经验建立某装备涡扇发动机的贝叶斯网络测试性模型，如图2所示。

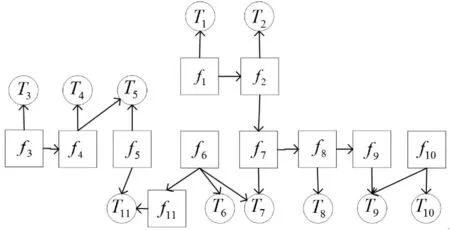
图2 发动机的贝叶斯网络测试性模型

图中为Ti为可以布置的测试，fj为发动机组件故障如表1所示，两者之间的相关关系由专家经验、试验仿真数据以及所选传感器性能特性决定。

表1 组件故障名称表

使用针对该模型的遗传算法，设置种群数量100，交叉概率0.5，变异概率0.01，种群经过300代选择繁衍后，对基因进行解码，得到最优的测试配置。

根据测试性设计要求：故障检测率FDR达到95%，故障隔离率FIR为80%，测试配置及分析如图3与表2所示。

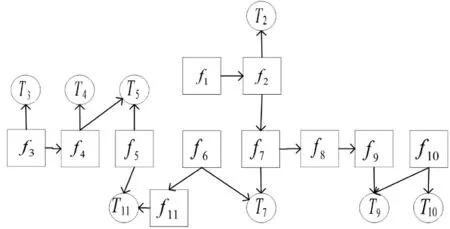
图3 测试配置方案

表2 测试配置指标分析

故障检测率FDR达到90%，故障隔离率FIR为70%，测试配置及分析如图4与表3。

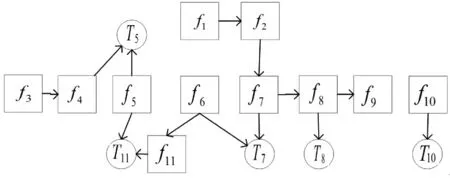
图4 测试配置方案

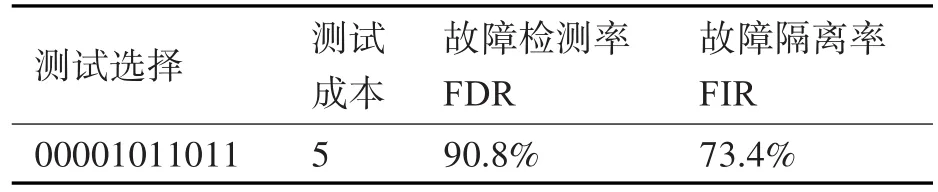
表3 测试配置指标分析

通过以上实例可以看出，该算法可以较好地完成贝叶斯网络测试性模型的测试配置任务，在减少测试数量的同时，满足装备测试性要求。运用该方法，可以减少研究人员工作量，提高测试性设计效率。

6 结语

基于贝叶斯网络的测试性模型是近年来研究的热点问题，本文针对该模型存在的尚无具体方法指导测试配置的问题，采用了基于遗传算法的贝叶斯网络测试性模型测试配置方法。该方法可在所提出测试性指标的基础上，给出满足要求的配置方案。但在研究过程中，该方法也存在一定的问题，比如计算速度慢，后期可以通过与其他算法的结合，改善该算法。