基于压缩传感的水下目标方位估计方法*

（杭州应用声学研究所声纳技术重点实验室 杭州 310023）

1 引言

声信号的波达方向（direction-of-arrival，DOA）估计是声纳在目标探测过程中非常重要的一个环节，它可以估计水下目标的空间方位。常规波束形成（conventional beamforming，CBF）［1］是 DOA 估计的传统方法，其分辨力受到瑞利限的限制。为了突破这一限制，发展起了一些高分辨的空间谱估计方法，如基于子空间分解的多重信号分类（multiple signal classification，MUSIC）方法［2］。除此之外，为了自适应地抑制干扰，基于最大信噪比准则的最小方差无失真响应（Minimum Variance Distortionless Response，MVDR）方法［3］可以自适应地估计DOA。无论是MUSIC方法还是MVDR方法，都需要计算信号的协方差矩阵，这导致了低快拍数、相干源、低信噪比条件下的性能下降。

2006年前后，压缩传感（compressive sensing or compressed sensing）又称为压缩采样（compressive sampling）发展起来。E.Candès和 T.Tao等［4～6］证明了，利用信号的稀疏性，能够用比Nyquist-Shannon采样定理所要求的少得多的采样实现稀疏信号的完全重构，因此取名压缩采样。同时期，D.Donoho等［7］提出了一种新的信息获取指导理论，即压缩传感。CS用于求解欠定线性逆问题，致力于发展信号的稀疏性或可压缩性，用比Nyquist采样率更低的采样率做采样而实现信号的重构。稀疏性或可压缩性是信号的自然性质，声信号的稀疏性或可压缩性表现在时域、频率域、空间域、波数域、空间波束域等域中。传统DOA估计方法的目标是使重构信号的能量最小，因而得到的是低分辨力、非稀疏的解。将CS应用到声信号的DOA估计中正是利用了空间波束域的稀疏性，因此得到的是高分辨的稀疏解。李璇等［8］分别利用对角加载最小二乘、λ1正则化和正交匹配追踪方法求解单快拍情况下的DOA估计问题，得到了高分辨的方位估计结果。房云飞等［9］提出了一种基于波束域的多重测量向量欠定系统正则化聚焦求解DOA的算法，结果表明有较好的估计精度和角度分辨力。A.Xenaki和P.Gerstoft等［10～11］把单快拍和多快拍情况下的 DOA估计分别建模为单一测量向量和多重测量向量的问题，结果表明CS方法的性能优于传统的波束形成和高分辨力方法。

本文将针对阵元间距大于半波长的线阵，即空间采样率低于Nyquist采样率进行研究。首先把DOA估计建模为一个标准的CS问题，并分析传感矩阵的相干性（coherence），然后利用凸优化方法［12～13］和基于阈值的方法［14］对DOA估计这一欠定线性逆问题进行求解。数值仿真结果和实验结果均表明了基于CS的波束形成方法的可行性，其分辨力要高于传统的DOA估计方法，可在单快拍、相干源、低信噪比条件下估计目标的空间方位。

2 压缩传感理论

经典的Shannon采样定理以带宽为先验信息，是一个充分非必要条件，对于频率低于最高频率的分量，一个周期上采的样本多于两个，因此存在冗余。空间采样亦是如此，阵元间距为最高频率的半波长时，那么小于最高频率的波长，一个周期上有两个以上的样本，存在冗余。对于传统的信号处理，在时域按Nyquist-Shannon采样较容易实现，但由于实际中信号带宽较大或最高频率较高使得采样频率也较高，因而采集到的数据量较大；在空间域上按Nyquist-Shannon采样需要在空间内均匀地布放大量传感器，成本太高。压缩传感从根本上颠覆了Nyquist-Shannon采样定理，在信号满足稀疏性或可压缩性的条件下，直接对信号进行压缩采样，通过复杂度较高的重构算法来重构原始信号。

压缩传感有三个基本要素，分别是稀疏性和可压缩性、压缩采样和重构算法。

1）稀疏性和可压缩性

一个信号如果在某一域中的分量大多数为零，则称这个信号是稀疏的。数学上，用λ0范数表示非零元素的个数，如果向量x∈CN最多有s个元素是非零的，就称 x是s-稀疏的，表示为‖x‖0≤s。稀疏性是一个强约束，实际中的许多信号是可压缩的。可压缩性指信号可以很好地由稀疏信号近似表示，这种表示常常是在经过适当的基变换之后，如Fourier变换、小波变换等。假设信号z∈CN可由稀疏向量x∈CN表示为

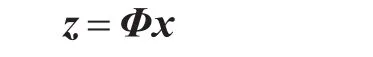
其中Φ∈CN×N称为变换基矩阵。

2）压缩采样

利用测量矩阵Ψ∈CM×N对信号z进行采样，得到测量数据y∈CM为

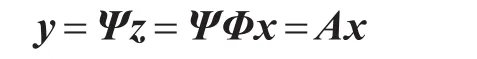
其中 A∈CM×N称为传感矩阵，是变换基矩阵和测量矩阵的结合。测量矩阵Ψ可以是随机的，也可以是确定的，其行数M一定小于列数N，故该采样过程把一个高维信号变换为低维数据，因而称为压缩采样。

3）重构算法

经过压缩采样后得到了一个欠定线性方程

压缩传感的目的是利用稀疏性，从少量的测量数据y中重构x或z，本质是求解该欠定线性方程的稀疏解。重构算法能够在适当的假设下，求得上述欠定线性方程的稀疏解。要想保证重构算法能准确地和有效地重构信号，传感矩阵A需要满足一定的性质，如零空间特性（null space property，NSP）、约束等距特性（restricted isometry property，RIP）和相干性等，其中前两者在计算上都是NP-hard的，因此论文中考虑相干性。重构算法可以粗略地分成三类：优化方法，贪婪方法和基于阈值的方法。

3 基于压缩传感的DOA估计方法

3.1 线阵DOA估计的CS模型

假设声源位于线阵的远场，即线阵接收到的声波可以考虑为平面波，考虑声源辐射的声信号是窄带的。线阵示意图如图1所示。

根据图1示意图，目标声源的DOA由相对于阵列方向的 θ∈[-90°，90°]决定。第i个声源对每个传感器的传播时延可以由驾驶向量表示：

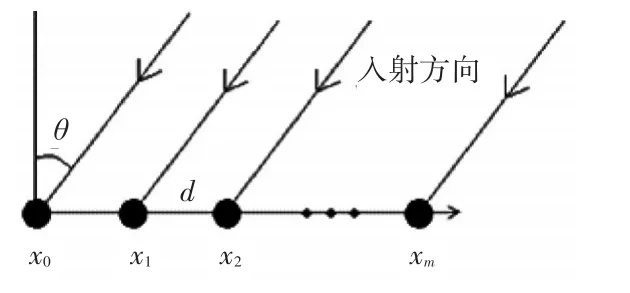
图1 线阵示意图

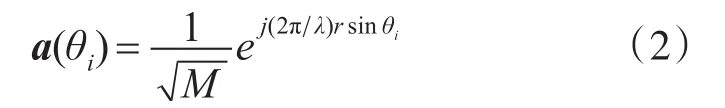
令向量x∈CN由感兴趣方向θ格点上的源信号幅度组成，y表示声场在M个传感器处的测量向量。由于我们感兴趣的是角度格点上的高分辨力，因此有M＜N。传感矩阵则由所有可能方向的驾驶向量组成，即

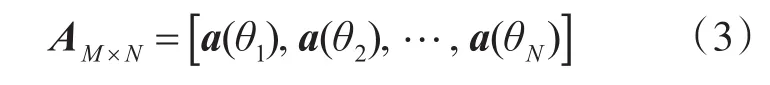
它是测量矩阵Ψ和基变换矩阵Φ的乘积，其中Ψ表示声场在传感器位置处的空间采样，是一个确定的矩阵，Φ表示一个IDFT变换基。考虑存在噪声n∈CM的情况，测量向量就可以表示为

这是一个标准的欠定线性系统，我们的目标就是利用x的稀疏性，从y中重构x。

3.2 优化方法和基于阈值的方法

CS中求解式（1）的问题被称为（P0）问题，它属于非凸优化问题，且一般是NP-hard的，因此通常把（P0）问题凸松弛为（P1）问题，表示为

（P1）问题是一个凸优化问题，常被称作λ1最小化或基追踪（basis pursuit，BP）。对于存在噪声的情况，可以利用Lagrange乘子法求解式（4），被称为问题，表示为

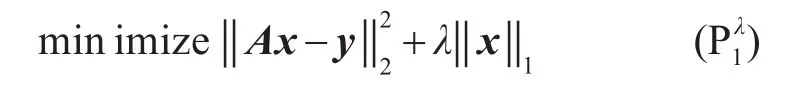
其中正则化参数λ＞0控制着稀疏解和测量值拟合之间的相对重要性。求解问题的方法被称作基追踪去噪（basis pursuit denoising，BPD）。在Matlab上可以利用CVX工具箱求解上述凸优化问题，它利用内点求解器得到优化问题的全局解。

除了优化方法，还有一种基于阈值的方法。由于λ0最小化是非线性操作，因此基于阈值的方法需要定义一个非线性算子Hs，它称为稀疏性为s的硬阈值算子。对于一个向量x，Hs（x）保持x的s个绝对值最大的元素不变，其他元素置为零。这里介绍一种已知解是s-稀疏情况下的迭代算法，称为迭代硬阈值（iterative hard thresholding，IHT）。该算法是通过迭代地求解定点方程xn+1=(I-AHA)xn+AHy得到的，其中I为单位阵，这里的上标“H”表示矩阵的共轭转置。由于已知所求的解是s-稀疏的，所以只需在每次迭代时保留s个绝对值最大的元素，最终可以得到一个s-稀疏的向量。

3.3 传感矩阵的相干性分析

传感矩阵A的特性会影响重构算法的性能。如果不考虑噪声，NSP是稳健的信号重构的充要条件。如果考虑存在噪声，Candès和Tao引入了RIP［15］，它对于各种算法成功地从有噪测量中重构一个稀疏信号是充分非必要的。无论是RIP还是NSP，它们在计算上都是NP-hard的，因此这里考虑易于计算的矩阵A的相干性［16］。相干性度量了传感矩阵任意两列之间的相关性（correlation），首先给出一个矩阵A的相干性μ(A)的定义式为

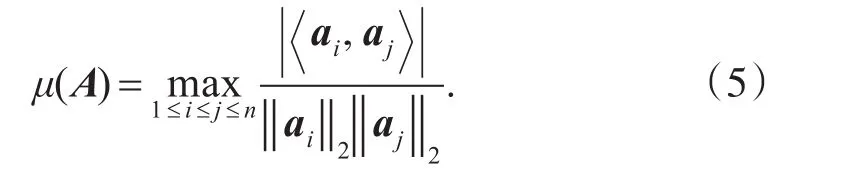
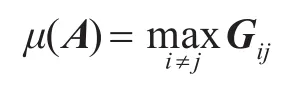
对于式（3）所表示的传感矩阵，有

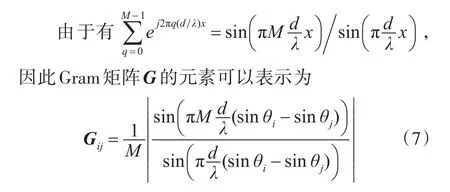
在DOA估计中，为了实现高分辨力，通常需要精细的格点，因此欠定方程中的传感矩阵A具有线性相关的列，其相关程度反映在G的非对角元素上。下面给出了阵元间距大于半波长的线阵的Gram矩阵示意图。

从图2中可以看出当d=4λ5时，不出现栅瓣的范围大约是[-15°，15°]。但是由于CS重构算法是非线性的，且稀疏解具有唯一性，因而在一定程度上可以准确重构出稀疏信号。

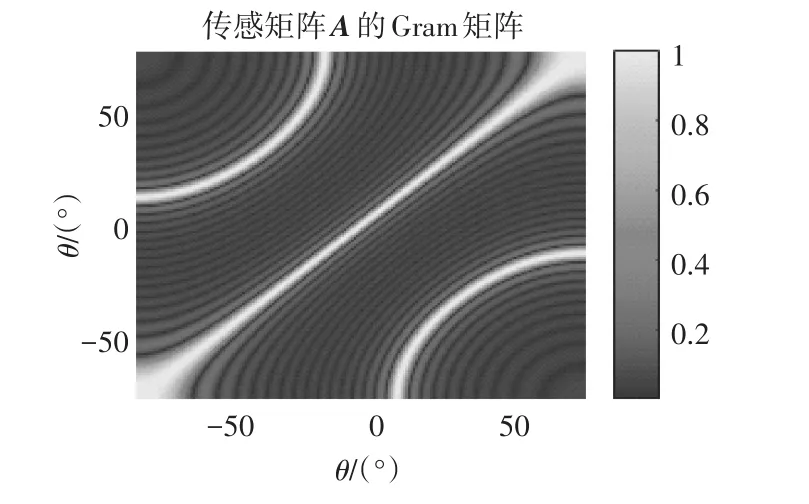
图2 十六元均匀线阵的Gram矩阵示意图，d/λ=4/5

4 数值仿真和实验结果

4.1 数值仿真结果

考虑一个16元均匀线阵，阵元间距d=4λ/5。首先考虑远场存在一个目标，入射方向为20°，信噪比为10dB，分别采用CBF、MVDR、MUSIC、BPD和IHT算法进行DOA估计。仿真结果如图3所示，其中CBF、MVDR和MUSIC算法的快拍数为50，BPD和IHT算法采用单快拍。从图3中可以看出，CBF和MVDR方法会在-65.3°出现栅瓣，虽然IHT算法仍然存在栅瓣，但BPD算法在一定程度上可以准确估计目标方位。因此基于CS的DOA估计可以在单快拍的条件下准确重构出目标方位，且分辨力高于CBF和MVDR。

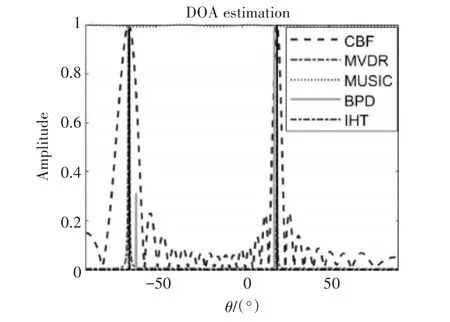
图3 单目标DOA估计

然后考虑存在两个相干源，入射方位分别为0°和5°，信噪比为-5dB，其余条件与之前一致，结果如图4所示。从图4中可以看出基于CS的DOA估计方法可以在相干源、低信噪比的条件下基本准确估计目标方位，且分辨力高于经典方法。

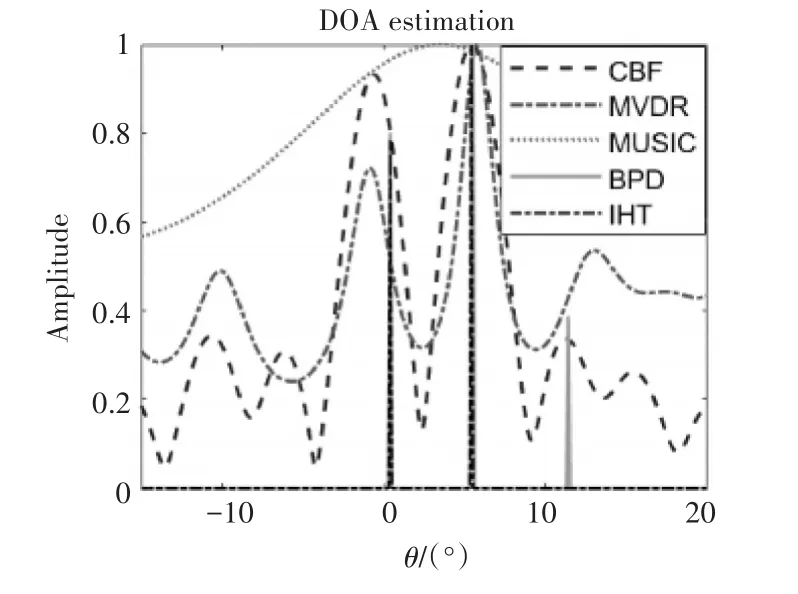
图4 相干源DOA估计

4.2 实验结果

在消声水池中进行水下目标方位估计的实验，目标是一块长2.35m，宽0.5m的铁板。利用收发合置形式的主动声纳对目标进行探测，发射中心频率为12kHz的PCW信号，脉冲宽度为10ms，用16元垂直线阵接收回波信号，阵元间距为0.1m，静止目标与接收阵之间的水平距离为25m。实验的目的是从接收到的回波信号中估计目标的空间方位，即目标的俯仰角。分别利用CBF、MVDR、BPD和IHT算法对目标的俯仰角进行估计，结果如图5所示。其中CBF和MVDR用了100个快拍，两者估计得到的俯仰角均为-1.3°，BPD和IHT计算了50个快拍，BPD估计的俯仰角均值为-1.3°，IHT估计的俯仰角为-1.5°，这些方法估计得到的结果与实际相符。可以看出，基于CS的DOA估计方法可以在阵元间距大于半波长的情况下有效估计目标的空间方位，尤其是在低快拍数的情况下，且分辨力高于经典的CBF和MVDR方法。

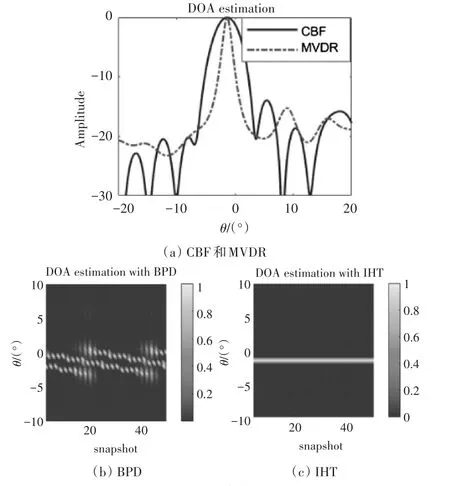
图5 实验结果

5 结语

本文将CS应用到线阵的DOA估计上，尤其是阵元间距大于半波长的线阵，把DOA估计转变为一个欠定线性方程，阐述了基本原理和基本的重构算法BPD和IHT，并分析了传感矩阵的相干性。数值仿真结果和实验处理结果均表明了BPD和IHT方法的有效性，尤其是在相干源、低信噪比、低快拍数的情况下，基于CS的DOA估计方法相较传统的CBF和MVDR等方法具有更高的分辨力，能较好地估计目标空间方位。