带防撞栏杆扁平箱梁高阶模态涡激振动的CFD研究
2021-06-03祝志文石亚光
祝志文, 石亚光, 颜 爽
(1. 汕头大学 土木与环境工程系,广东 汕头 515063; 2.中冶南方工程技术有限公司,武汉 430000)
现代桥梁跨度的不断增大使得结构逐步向轻柔化和低阻尼方向发展,导致其对风致作用更加敏感。使得其在常遇风速下存在发生涡激振动的可能。涡激振动是一种具有自激和自限幅特性的风致振动,已建成的丹麦大带东桥[1],日本东京湾大桥[2],巴西Rio-Niteroi桥[3]和西堠门大桥[4]均发生过大幅度的涡激振动。2020年5月5日广东虎门大桥多次发生涡激振动,引起社会广泛关注。当桥梁跨度大于1 000 m后,结构基频很小且模态密集,在常遇风速内可依次激发桥梁主梁的多个模态,也即可激发基频以上的桥梁高阶模态振动[5-6]。桥梁涡激振动虽不如颤振一样导致桥梁的灾难性破坏,但会影响桥面行车的舒适性和安全性,过大的涡振所产生的高应力幅可能会在桥梁主体结构的焊缝部位产生疲劳破坏。因此,准确预测大跨度桥梁的涡激振动并采取有效的预防措施显得尤为重要。
现阶段桥梁涡激振动研究主要借助节段模型风洞试验[7-9],但节段模型试验获得的主梁最大涡激振动幅值可能与实桥存在差别,因而可能需要修正,其中的途径如通过节段模型结果与多点弹性支承模型的对比得到[10-11]。现有涡激振动数值模拟的研究也主要集中在形状规则的断面上,如圆柱、方柱和椭圆等。Daniels等[12]采用大涡模拟(large eddy simulation,LES)方法结合动网格技术对长宽比为4的矩形柱进行了涡激振动数值模拟。徐枫等[13]采用二维RANS(Reynolds-averages Navier-Stokes)方法模拟了不同截面形状弹性支撑柱体的流致振动,结果表明柱体的振动以横向振动为主。Seyyed等[14]针对低雷诺数下的椭圆涡激振动进行了二维模拟,并分析了不同攻角和不同椭圆外形对涡激振动的影响。对桥梁涡激振动的计算流体动力学(computational fluid dynamics,CFD)模拟,特别是包含防撞栏杆等附属设施的成桥状态断面开展得非常少,且鲜见针对带防撞栏桥梁主梁高阶模态涡激振动的CFD研究报道。
本文以大跨度桥梁较为普遍采用的闭口扁平箱梁为例,采用分区网格划分策略解决桥梁振动过程中容易出现的网格畸变问题,并将求解桥梁涡激振动响应的Newmark-β法通过自开发的UDF程序嵌入到Fluent中,开展了大带东桥扁平箱梁断面的高阶模态涡激振动模拟,得到了高阶模态涡振锁定曲线并在此基础上对涡激振动的影响因素进行了分析。
1 基准模型CFD模拟的数值实现
在1999年6月24日召开的第10届国际风工程会议上,国际风工程协会确定丹麦大带东桥主桥加劲梁作为桥梁CFD模拟的基准模型[15]。该加劲梁为扁平六边形闭口箱梁,梁宽31 m,高4.4 m,桥面布设钢制中央分隔栏和上下游侧栏杆,如图1所示,其中S.C.代表加劲梁剪切中心,在桥轴线距离底板0.535倍加劲梁梁高位置。需要指出,早期关于大带东桥CFD研究的诸多文献,由于方案的变更导致一些研究的加劲梁气动外形与成桥不一致的情况,包括梁宽和栏杆外形等。需要指出,该桥在4~12 m/s的风速下就曾发生了显著的多阶竖向涡激振动,包括高阶模态涡激振动。
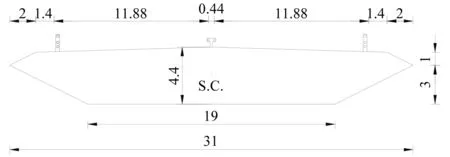
图1 大带东桥主跨加劲梁断面(m)Fig.1 Stiffening girder cross section of main span of Great Belt East Bridge(m)
1.1 控制方程
计算风工程中,桥梁绕流问题的二维黏性不可压雷诺时均Navier-Stokes方程表示为
(1)
(2)
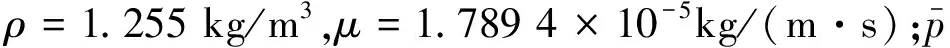
SST(shear stress transport)k-ω湍流模型,结合了标准k-ε模型和k-ω模型的各自优点,在外部自由流中采用k-ε模型,在近壁区采用k-ω模型。一般认为SSTk-ω湍流模型是雷诺时均模型中求解精度最好的湍流模型之一,计算量也显著小于大涡模拟。由于本文涡激振动模拟涉及大量时间步上的非定常计算,综合计算量和计算精度,本文数值模拟采用SSTk-ω湍流模型。
为模拟高阶模态涡激振动,本文针对大带东桥实际观测到的第八阶竖弯涡激振动开展研究。为此将加劲梁断面竖向涡激振动系统简化为单自由度的弹簧-质量-阻尼系统,如图2所示,其中α表示来流风攻角。其竖弯运动方程表示为
(3)

利用Newmark-β法求解式(3)的运动微分方程,对下一时刻t+Δt,振动控制方程可以写为
FL(t+Δt)/M
(4)
式中,Δt为时间步长。因此,在t+Δt时刻的位移、速度和加速度可以表示为

(5)
(6)
其中,

(8)
(9)
式(5)~式(9)中的a0,a1,a2,…,a7均为常数,取值为
(10)

a7=βΔt
(11)
研究表明,当β≥0.5且γ≥0.25(0.5+β)2时,Newmark-β法将无条件稳定,因此系数β与γ本文分别取为0.5和0.25。
桥梁涡激振动为流固耦合问题,本文采用如图3所示的分析流程。也即先通过Fluent求解扁平箱梁绕流的Navier-Stokes方程,得到作用在扁平箱梁上的升力,再基于Newmark-β求解加劲梁的运动方程,获取加劲梁的振动位移、速度和加速度,然后通过Fluent宏更新加劲梁姿态并重新进行网格划分,再进入下一个时间步上计算域的求解,依次循环,如图3所示。

图2 加劲梁涡激振动模型Fig.2 Vortex-induced vibration (VIV) model of stiffening girder

图3 涡激振动分析流程Fig.3 Flowchat of simulation of VIV
1.2 计算域及CFD相关参数设定
大带东桥主桥加劲梁断面CFD模拟的计算域,如图4所示。CFD模拟的箱梁采用1∶80的缩尺比,并考虑了上下游栏杆和中央防撞栏。计算域的入口、上侧和下侧边界到加劲梁剪切中心的距离均为10B,出口到断面剪切中心的距离为25B,对应的模型堵塞度为0.72%,显著小于风洞试验模型堵塞度的要求。为保证模型运动时网格的质量,本文采用“刚性运动区域+变形网格区域+静止网格区域”的方法对计算区域进行分区网格划分。在扁平箱梁外围划分一个椭圆形区域,椭圆形区域的中心与扁平箱梁剪心重合,内部采用结构化网格,栏杆及分隔带附近区域为非结构化网格,整个椭圆形区域作为刚体随扁平箱梁一起运动。因此,只有与椭圆区域相连的外部变形区域网格发生重构,而紧邻模型表面的边界层网格采用固定不变的高质量网格。通过用户自定义函数给定椭圆区域内刚性网格的运动方式,变形域内的非结构化网格通过“弹簧光顺”和“区域重构”进行更新;另外,静止网格区网格固定不动,并采用结构化网格划分。
节段模型风洞试验评价桥梁的涡激振动通常基于均匀来流条件。为此,本文计算域入口边界采用水平均匀流速度,出口边界设置为压力自由出流;扁平箱梁表面为无滑移壁面,上下边界均设置为对称边界。采用入口速度对初始流场进行全局初始化。数值计算采用循序渐进的模拟方法,以平抑初始场计算导致的数值振荡,并最终转到SSTk-ω湍流模型计算,此时计算采用非定常二阶隐式格式,采用速度-压力解耦的SIMPLEC算法;动量方程、湍动能方程及耗散率方程均采用QUICK格式。数值模拟时先进行扁平箱梁断面的静止绕流计算,待流场收敛后,再导入用户自定义函数进行扁平箱梁的高阶涡激振动模拟。
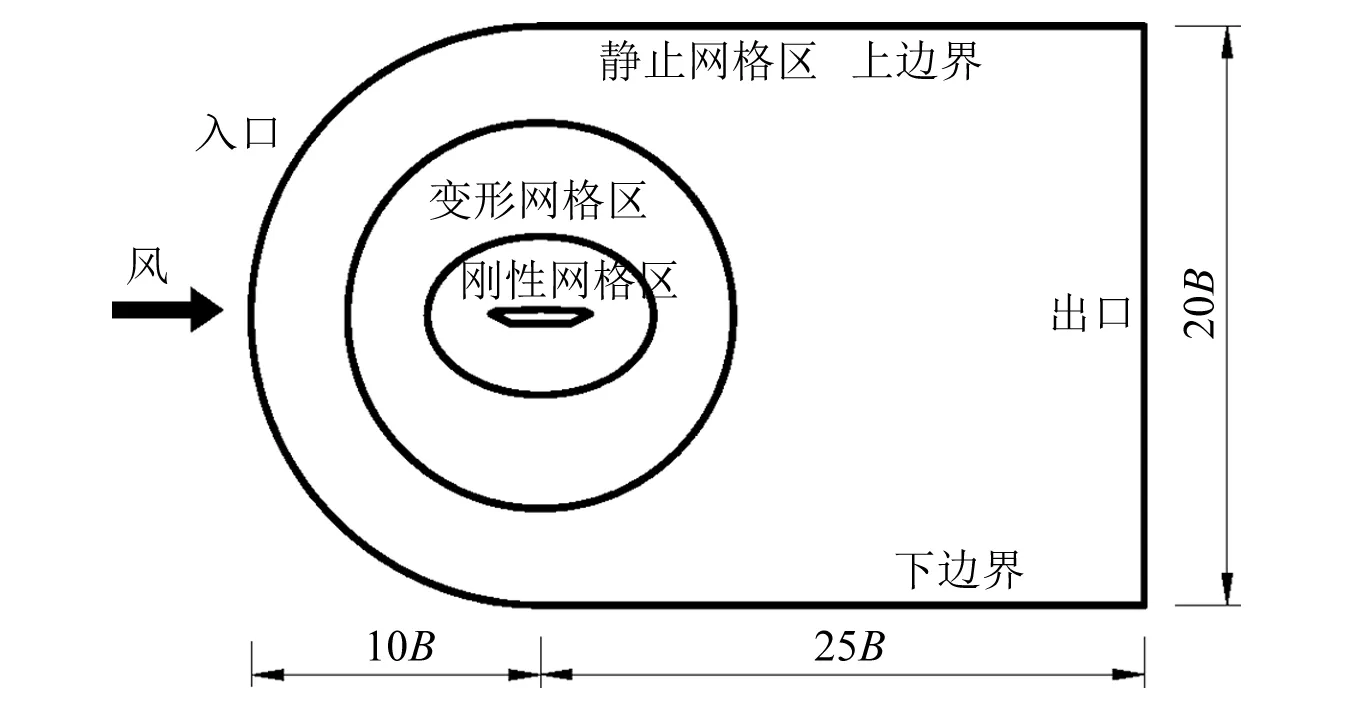
图4 计算域分区Fig.4 Computational domain partition
1.3 网格及时间步长无关性检查
合适的网格划分对CFD精确模拟至关重要。为此,本文基于G1,G2和G3三套网格开展了网格无关性检查。相关网格参数见表1所示。三套网格均满足SST湍流模型对边界层网格的要求(Y+<1),其中最粗网格G1的物面最大Y+为0.96,位于模型前缘附近,如图5所示。

图5 G1网格主梁表面Y+分布Fig.5 Distribution of Y+ on girder surface of mesh G1
另外,以G2网格为例,通过GAMBIT之EquiAngle Skew评价的网格优良质量(0~0.25)率为96.25%,而网格质量为好的百分率(0~0.5)达到100%。G2网格方案扁平箱梁周围网格划分见图6;为提高节段模型前缘所划分网格的正交性、保持网格边长的平顺变化并显著减小网格数量,对前缘棱角采用半径B/1550的圆化处理,这种处理对主梁气动特性的影响可忽略不计[16]。图7展示了扁平箱梁前缘、中央防撞栏及上游栏杆周围网格划分细节,下游栏杆网格布置与图7(c)相同。

图6 G2网格在模型周围的分布Fig.6 Arrangement of G2 mesh around stiffening girder
扁平箱梁断面的气动升力系数CL、阻力系数CD和斯托罗哈数St分别定义为
CL=FL/(0.5ρU2B);CD=FD/(0.5ρU2B);
St=fsH/U
(12)
式中:U为计算域入口来流风速;FL和FD分别为作用在加劲梁单位长度上的升力和阻力;fs为漩涡脱落频率;H为扁平箱梁迎风高度。


图7 G2局部位置网格放大Fig.7 Close-up view of G2 mesh at local position

表1 不同网格固定模型绕流模拟结果Tab.1 Numerical results of flow around stationary stiffening girder on different grid arrangement

表2 自由振动模型网格无关性检查结果Tab.2 Numerical results of grid independence check for free oscillating stiffening girder
考虑时间步长的合适取值,本文采用G2网格,计算了0°攻角下四个不同时间步长0.001 s,0.002 s,0.005 s和0.010 s上的静止绕流场,雷诺数为4×104。表3给出了不同时间步长的模拟结果,可见当时间步长小于0.002 s时,气动力系数平均和脉动值趋于稳定。另外,对4°攻角下的扁平箱梁断面涡激振动绕流开展了0.002 s和0.001 s两个不同时间步长下的数值模拟,模拟结果如表4所示,两个时间步长上的模拟结果误差很小,因此认为采用0.002 s的时间步长是合适的。表3将模拟结果与Larsen和祝志文等的风洞试验结果进行了对比,可见本文数值模拟得到的漩涡脱落St数及阻力系数均值均与风洞试验值吻合。

表3 不同时间步长静止绕流数值结果Tab.3 Numerical results of stationary stiffening girder under different time step size

表4 自由振动时间无关性研究数值结果Tab.4 Numerical results of time independence check of stiffening girder under free vibration
2 数值模拟结果
Larsen给出了大带东桥节段模型风洞试验获得的实桥第八阶竖向涡激振动的完整锁定曲线,见图8。Larsen研究中节段模型试验结构参数如下:模型宽度B和高度H分别为0.387 5 m和0.055 m,第八阶模态质量M=3.553 kg/m、模态频率fn=3.9 Hz和模态阻尼比ζ=0.16%,来流风攻角为4°。
2.1 涡激振动锁定曲线
定义折减风速为Vr=U/(fnB),本文对折减风速在0.6~1.8内的扁平箱梁高阶涡激振动进行了数值模拟。从图8无量纲涡振振幅RMS(root mean square)随折减风速的变化可见,大带桥加劲梁第八阶模态存在两个涡振锁定区间,高折减风速涡振锁定区间与试验有较好的一致性,表现出高阶涡振幅值在锁定区间内先增大后减小的自限幅特征。低折减风速涡振锁定区间在Larsen研究中没有体现,这可能与风洞试验风速缩尺比较大,而低折减风速涡振锁定区风速太小有关。实际上对不少风工程风洞,试验段风速开始稳定的风速较高,可能高于试验风速缩尺对应的实桥涡振风速,因此将无法搜索出低折减风速涡振锁定区。这显示了CFD模拟捕捉涡振研究上的优势。

图8 无量纲涡振振幅RMS随折减风速的变化Fig.8 Non-dimensional RMS value of VIV versus reduced velocity
图9(a)~图9(c)分别为图8中第二个高阶涡振风速锁定区间的起始点、上升点和最高点对应的加劲梁断面高阶涡激振动响应时程曲线,折减风速分别为0.93,1.12和1.26,图中重力加速度g=9.8 m/s2。从图9中可以看出,高阶涡激振动时程曲线均是振幅先增大后趋于稳定。图10(a)~图10(c)分别给出了三个折减风速下,加劲梁断面升力时程的归一化功频谱密度(power spectral density,PSD)曲线。可见三个卓越频率皆与结构的自振频率3.9 Hz接近,即桥梁结构频率在较宽的风速范围内“锁定”了扁平箱梁的高阶漩涡脱落频率。

图9 不同折减风速下的涡激振动响应Fig.9 VIV response under different reduced wind velocities

图10 不同折减风速下的归一化升力系数功率谱Fig.10 Normalized PSD of lift coefficient time histories under different reduced wind velocities
图11和图12分别为锁定区间峰值点,即折减风速为1.26时,高阶涡激振动达到稳定状态后一个周期内升力系数和振动位移时程曲线,以及扁平箱梁断面漩涡脱落云图。从图可见,升力时程曲线与位移时程曲线并不完全同步,位移曲线滞后力系数曲线5°~10°的相位差。图12(a)~图12(d)描述了一个周期内扁平箱梁断面周围漩涡的形成与发展过程(n为正整数),可见漩涡从扁平箱梁前缘和上游侧栏杆形成,随后沿箱梁顶面向下游漂移,并最终在下游侧栏杆处脱落的过程。另外,高阶涡振一个周期内箱梁下表面未见明显的漩涡形成和运动,可见上下游侧桥面栏杆对扁平箱梁断面漩涡的形成和脱落有重要影响,因此,大跨度桥梁需特别重视上下游侧桥面栏杆的气动外形设计。

图11 一个振动周期内升力及位移时程曲线Fig.11 Lift and displacement time histories during one cycle of VIV

图12 涡振锁定区一个周期内的漩涡脱落云图Fig.12 Vortex-shedding contours during one cycle of VIV
2.2 涡激振动影响因素


表5 阻尼比对高阶涡激振动响应的影响Tab.5 Effects of damping ratios on VIV response
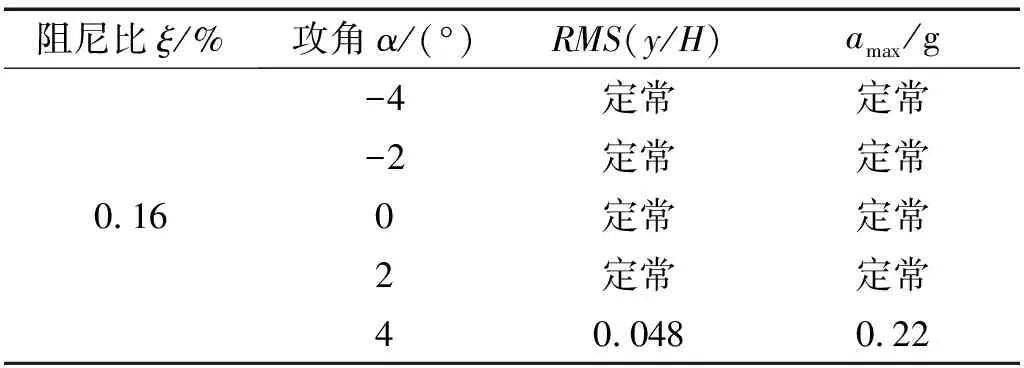
表6 攻角对高阶涡激振动响应的影响Tab.6 Effects of wind angles of attack on VIV response
3 结 论
本文开展了雷诺数为3.18×104~6.10×104的扁平箱梁高阶模态涡激振动响应的CFD模拟,得到如下结论:
(1)采用本文CFD模拟和结构响应计算的耦合方法,能有效预测扁平箱梁的高阶模态涡振锁定区间和涡振幅值;在低折减风速涡振锁定区的识别上,CFD方法可能优于风洞试验。
(2)高阶模态涡激振动表现出与阻尼和来流风攻角的相关性。当阻尼比增大时,高阶模态涡振逐渐减小甚至消失;另外,在研究的风攻角范围,而只有当来流风攻角大于2°时,才能观察到扁平箱梁明显的高阶涡激振动。
(3)上下游桥面栏杆对扁平箱梁上表面漩涡的产生和脱落有重要影响,因此,从预防涡激振动发生的角度,大跨度桥梁需特别重视上下游桥面栏杆的气动外形设计。
由于计算资源的限制,本文仅开展了二维CFD模拟,进一步研究可考虑扁平箱梁三维CFD模拟。当未来计算资源足够时,甚至可尝试开展加劲梁真实的高阶模态涡激振动模拟。
