基于多体接触瞬态动力学支承不同心模拟分析方法
2021-06-03柏长青左彦飞耿斌斌胡明辉
柏长青, 左彦飞, 耿斌斌, 胡明辉
(1. 北京化工大学 发动机健康监控及网络化教育部重点实验室,北京 100029;2. 北京化工大学 高端机械装备健康监控及自愈化北京市重点实验室,北京 100029; 3. 中国航发动力所-北京化工大学 航空发动机振动健康监控联合实验室,北京 100029)
燃气涡轮发动机支承不同心故障会导致转子运动轨迹的偏移、轴承的偏载,进而引发剧烈的整机振动[1],是发动机振动超标的主要原因之一[2]。
针对转子的不同心以及与之类似的不对中故障,现有研究大致可分为两类:第一类是利用变形和力学关系求解不同心或不对中故障的等效激励作为系统动力学微分方程中的激励项;求解并分析系统的运动微分方程,发现2倍频与复杂的轴心轨迹是不同心与不对中故障的主要特征[3-4];第二类直接建立不同心或不对中状态下转子系统的能量方程,求解并分析故障特征,发现在支承不同心故障下,其响应频谱中不仅会产生1倍频、2倍频特征还会出现高次谐波分量[5]并且不同心故障会导致连接结构的刚度非线性[6-8],不对中故障是转子横向和扭转激励的来源之一[9-10]。上述两类主要是基于宏观运动和转子动力学分析得到典型2倍频特征与复杂轴心轨迹,为不同心故障的诊断提供了依据。不过对于燃气涡轮发动机等复杂双转子机匣系统,仅依据频谱特征中的1倍频及2倍频分量还很难诊断不平衡、不同心故障。
由振动传递路径分析可知,不同心激励必然通过轴承作用于机匣支承上,轴承滚珠与外圈的复杂力学作用是机匣测点不同心故障特征产生的直接激振源。因此,通过轴承复杂接触瞬态分析可能获得更全面的不同心故障特征产生机理及规律。
近几年,基于多体动力学的轴承复杂接触状态分析已受到关注。李长健等[11]、刘雅雯[12]分别建立了故障轴承的多体动力学模型,对轴承故障特征进行了深入分析。张宇超等[13]建立了深沟球轴承与转子系统的多体动力学模型,用于评估转子轴承系统的稳定性。本文在此基础上,建立了带有中介轴承的典型发动机高压转子-轴承支承系统多体动力学模型,提出支承不同心等效模拟方法,通过轴承接触非线性模拟,支承柔性化等模拟不同心故障下轴承复杂接触运动状态,分析了轴承外圈与薄壁支承位置不同心故障特征产生机理及变化规律。
1 典型燃机高压转子不同心故障的模拟方法
1.1 高压转子-轴承-支承系统多体动力学建模
以带有中介轴承的典型燃机高压转子系统为研究对象,其具体结构如图1所示。该发动机高压转子系统由9级高压压气机盘、1级封严盘和1级高压涡轮盘组成。前支点(4号轴承)位于高压压气机Ⅰ、Ⅱ盘之间,轴承内圈与高压转子相连,外圈通过薄壁结构与中介机匣相连;后支点为中介滚棒轴承(5号轴承),支承在低压涡轮轴上。低压涡轮轴由两个支点(3号和6号轴承)支承,承受中介轴承的作用力。
基于ADMAS多体动力学软件,建立了图1高压转子及轴承支承系统的多体动力学模型,如图2所示。图中高压转子主体、轴承内外圈、滚珠、保持架等均按实际结构尺寸和材料参数建模,支承轴承的几何尺寸参数见表1。高压转子简化了叶片,忽略了均压孔、销钉、螺栓、倒角等细节结构特征。经转子动力特性分析,在该发动机的工作转速范围内,高压转子主要表现为刚性转子特性,主要变形集中在弹性支承上,因此,将图2所示薄壁支承进行等效柔性化处理,保留模态阶次15,覆盖频率范围0~6 100 Hz,大约为该转子系统工作转速范围的27倍。

图1 高压转子几何结构图Fig.1 Structure of high-pressure rotor system

图2 高压转子多体动力学模型Fig.2 Multi-body dynamics model of high-pressure rotor

表1 支承轴承的几何尺寸参数Tab.1 Geometrical parameters of supporting bearings
1.2 高压转子系统支承不同心模拟方法
由于装配工艺及弹性支承的变形均可能导致转子支承结构发生∂角度偏移,使得4号、5号轴承产生Δh的高度差,出现高压转子的支承不同心现象,如图3所示。

图3 高压转子支承不同心故障示意图Fig.3 Bearing misalignment of the high-pressure rotor
而在1.1节中建立的是理想条件下高压转子支承系统多体动力学模型。为模拟不同心故障,文献[14]采用力矩分解的方式施加等效不同心激励,本文采用在涡轮附近的支点位置施加偏斜角为∂的驱动转速ω的方式近似模拟不同心激励。如图2所示,将施加在高压转子的驱动转速ω分解得到轴向的主驱动转速ωx以及由于不同心造成的径向驱动转速ωy,ωz。此时,高压转子的两个轴承在径向驱动转速的作用下,表现为复杂的接触和运动状态,形成不同心激励力与力矩。
1.3 轴承各部件之间的非线性接触力模拟
当施加不同心驱动转速后,由于转子偏离理想轴线转动,轴承的内圈相对位置发生变化,使得滚动体与内外圈的接触状态发生变化,从而产生约束反力和力矩,形成不同心激励。为模拟该不同心激励,需要准确模拟轴承各部件间的瞬态非线性接触力,图4为不同心故障下4号轴承受力分析图。

图4 不同心故障下4号轴承的受力分析Fig.4 Force analysis of No. 4 bearing under misalignment fault
图4(a)单个滚动体分析中Fij,Foj为第j个滚动体与内外圈的法向冲击力;fij,foj为第j个滚动体与内外圈的切向摩擦力;Fbj为第j个滚动体与保持架的法向冲击力;fbj为第j个滚动体与保持架的切向摩擦力;Fr为第j个滚动体的离心力;G为第j个滚动体的重力。轴承整体受力分析图4(b)中,轴承不仅承受来自转子的三个方向的不同心力Fx,Fy,Fz还承受三个方向的不同心力矩Mx,My,Mz。5号轴承为滚棒轴承,主要承受径向力,不能承受轴向力,其余受力与4号轴承相似,此处不再详细分析。
通过受力分析可以看出,滚动体与各部件的接触力主要包括法向冲击力与切向摩擦力两类。冲击力又由两部分组成:一部分是两个构件相互接触时产生的弹性力;另一部分是由于相对速度产生的阻尼力。本文根据impact函数提供的非线性等效弹簧阻尼模型来计算冲击力,其表达式为
(1)
式中:k为弹簧刚度;g为接触构件之间的穿透深度;上标e为力指数;dmax为最大允许穿透深度:cmax为当达到最大穿透深度时所对应的最大阻尼值,step(g,0,0,dmax,cmax)按照式(2)进行计算[15]
(2)
滚动体与内外圈的摩擦力可表示为
(3)
在轴承实际的运行过程中,滚动体与轴承内外圈之间不可避免会产生相对滑动速度。由库伦摩擦定律可知滚动体与内、外滚道的摩擦因数与相对滑动速度v有关,μ具体表达式[16]
(4)
式中:μs,μd分别为静摩擦因数和动摩擦因数;vs,vd分别为静摩擦转换速度和动摩擦转换速度。
1.4 系统多体接触瞬态动力学方程及求解

(5)
式中:T为系统动能,表达了在广义坐标qi下的约束反力;P为系统的广义动量;HTF为系统包括接触力与力矩在内的广义激励;Φ为约束方程的雅可比矩阵;λ为系统拉格朗日乘子。通过式(5)处理方式,将二阶微分方程降阶为一阶微分方程,然后求解[18]。
当高压转子系统发生支承不同心故障时,不同心激励通过转子的不规则运动作用到轴承上,改变滚动体与内外圈的接触状态,使得滚动体与内外圈的接触力在时域、频域上均发生较大变化。本文通过求解式(5)得到不同心激励下图5所示各个滚珠与外圈的瞬态接触力及其合力、合力矩,分析不同心作用下滚珠对外圈的作用力的时域、频域特征,得到不同心激励特征。
2 典型燃机高压转子不同心故障响应分析
在高压转子1级盘上施加不平衡块,使整个系统获得初始不平衡量,在此基础上,分别对高压转子施加不同心角度0°,0.02°,0.04°,0.06°,0.08°,时长0.2 s,共1 000步,计算高压转子100%工作转速(13 300 r/min≈222 Hz)下的运动状态。下文分别就单个滚珠、滚珠与轴承外圈、轴承外圈与支承结构的瞬态接触力、力矩以及支承结构振动响应,并且由于滚动体与保持架的接触力仅影响轴承转速的波动情况,并不影响不同心激励的传递,故下文并未分析。
2.1 单个滚动体与轴承内外圈的非线性接触力
图5~图8所示为4号滚珠轴承单个滚动体与内圈、外圈的接触力频域特征随不同心量改变的变化规律。对于轴向接触力,当只有不平衡激励时并无特殊频率成分,而当不同心与不平衡故障同时存在时,轴向力产生了一些复杂频率成分如32 Hz,94 Hz,127 Hz,221 Hz,442 Hz等,如图5、图7所示。对于径向接触力,无论是不平衡故障还是两种故障共同作用,滚动体与轴承内外圈均有上述特征频率,如图6、图8所示。同时,随着不同心量的增加,轴向与径向接触力频谱中上述频率的幅值均增大。

图5 单个滚动体与内圈的轴向接触力频域特征随不同心量改变的变化规律Fig.5 Frequency characteristics of the axial contact force between one roller and the inner ring varied with misalignment values

图6 单个滚动体与内圈的径向接触力频域特征随不同心量改变的变化规律Fig.6 Frequency characteristics of the radial contact force between one roller and the inner ring varied with misalignment values
进一步阐释上述特征频率的产生机理,以不同心量为0.08°计算结果为例,分析单个滚珠运动过程与接触力的时域变化对照关系,如图9所示。当高压转子发生支承不同心故障时,会使滚动体与轴承内外圈产生周期性的压紧和松脱现象。当浅色滚动体由位置1运动到位置3时,此时滚动体与内外圈的接触力由0到最大值再到0,在此阶段浅色滚动体处于压紧区,滚动体与轴承内圈处于紧密接触状态,在位置2处接触力达到最大。当滚动体由位置3运动到位置4时,此时滚动体由压紧区进入松脱区,故在此阶段滚动体与内圈的接触力为0,浅色滚动体由位置1到位置4时,滚动体经历了由压紧区到松脱区的周期性变化,周期约为0.007 9 s,频率约为127 Hz。
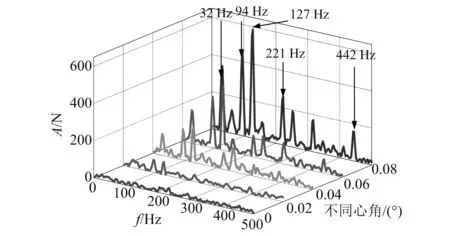
图7 单个滚动体与内圈的轴向接触力频域特征随不同心量改变的变化规律Fig.7 Frequency characteristics of the axial contact force between one roller and the outer ring varied with misalignment values

图8 单个滚动体与外圈的径向接触力频域特征随不同心量改变的变化规律Fig.8 Frequency characteristics of the radial contact force between one roller and the outer ring varied with misalignment values

图9 4号轴承与内圈径向接触力与滚动体位置关系图Fig.9 Radial contact force between one roller and inner ring and the position of the roller
当浅色滚动体继续到位置5,滚动体以地面参考坐标系公转一周后回到了初始位置,在接触力的频谱上产生了94 Hz的滚动体公转频率,但此时滚动体与内圈的相对位置与位置1不同,位置1与位置5处的接触力也不相同。当浅色滚动体继续经过位置5、位置6、位置7到达位置8,此时滚动体与地面和内圈的相对位置与位置1处相同,经历了一个完整运动周期,历时0.031 s,对应频率约为32 Hz。此外,由于周期性冲击等复杂相互作用的存在,转子的工频221 Hz及其倍频成分在频域上有所体现,但在时域上与滚动体的相对位置未找到明确的对应关系。
进一步分析发现,在没有不同心故障时,滚珠与内外圈接触力主要为径向接触力,当存在不同心故障后,接触力产生明显的轴向分量,致使轴向接触力出现32 Hz,94 Hz,127 Hz,221 Hz,442 Hz等明显频率成分。由于5号轴承并没有发生明显的位置变化,其滚动体与内外圈接触力的变化相对较小,故在这里不做分析。
2.2 滚珠—轴承外圈—支承间受力及传递规律
不同心激励通过转子—轴承内圈—滚动体—轴承外圈传递到柔性支承。因此,在单个滚动体的运动与受力分析的基础上,进一步分析所有滚珠与轴承外圈接触力合力,图10、图11所示为不同心量为0.08°时的计算结果。可以看出,虽然单个滚珠接触力工频及倍频成分并不突出,但所有滚珠与外圈的接触力合力则主要体现为工频及其倍频成分,由滚珠与外圈相对接触运动产生的32 Hz,94 Hz,127 Hz等特征频率基本相互抵消。轴向的合力中明显包含显著的工频及倍频成分,而径向合力主要包含工频成分,倍频成分并不明显。 此外,在时域上,轴向合力明显小于径向合力。

图10 4号轴承滚珠对外圈的轴向合力的时域波形与频谱Fig.10 Time-domain waveform and frequency spectrum of axial resultant contact force between outer ring and all rollers
在1.3节轴承整体受力分析中,滚珠对外圈作用除了轴向和径向力外,还包含轴向、径向力矩。不过,由于滚动体与轴承外圈的接触位置及接触力在运转过程中变化复杂,不易直接求得合力矩。实际上,由滚珠接触力合成的激励力及力矩都由轴承外圈通过约束传递到支承。为此,进一步分析轴承外圈与支承间的约束力及力矩计算结果,如图12~图 15所示。

图11 4号轴承滚珠对外圈的径向合力的时域波形与频谱Fig.11 Time-domain waveform and frequency spectrum of radial resultant contact force between outer ring and all rollers

图12 外圈与支承间轴向约束力时域波形与频谱Fig.12 Time domain waveform and frequency spectrum of axial restraining force between outer ring and support structure

图13 外圈与支承间径向的约束力时域波形与频谱Fig.13 Time domain waveform and frequency spectrum of radial restraining force between outer ring and support structure
从图12和图13可以看出,外圈与支承间的轴向及径向约束力在时域和频域上与图10、图11中滚珠对外圈的轴向、径向合力基本一致,径向力中的倍频成分依然相对较小。说明滚珠激励力的合力经轴承外圈传递后无明显改变。
从图14和图15外圈与支承间轴向、径向力矩时域波形与频谱可以看出,在滚珠激励力合力矩作用下,轴承外圈与支承间轴向力矩和径向力矩频谱都表现出明显的工频及倍频成分,幅值上工频成分最大,倍频幅值随倍数增大呈递减趋势。

图14 外圈与支承间轴向力矩时域波形与频谱Fig.14 Time domain waveform and frequency spectrum of axial restraining torque between outer ring and support structure

图15 外圈与支承间径向力矩时域波形与频谱Fig.15 Time domain waveform and frequency spectrum of radial restraining torque between outer ring and support structure
综上,全部滚珠与外圈的瞬态接触力合力及合力矩是不同心故障特征产生的直接激励源。轴向激振力频谱中明显包含工频及倍频成分;径向激励力明显大于轴向激励,但频谱中的倍频成分并不明显。而径向和轴向力矩频谱中均包含明显的工频及2倍频、3倍频成分。幅值上工频成分最大,倍频幅值随倍数增大呈递减趋势,4倍频之后幅值相对很小。
2.3 柔性支承上测点的振动响应
在上述轴承外圈与支承间力和力矩的综合作用下,柔性支承上测点的振动位移计算结果如图16、图17所示。在时域上,测点的径向振动位移大于轴向,均表现出明显的周期性。在频域上,轴向与径向振动位移均有高压转子工频及倍频成分。

图16 柔性支承测点轴向振动随不同心量变化规律Fig.16 Axial vibration on measuring points of flexible support varied with misalignment values

图17 柔性支承测点径向振动随不同心量变化规律Fig.17 Radial vibration on measuring points of flexible support varied with misalignment values
结合轴承位置的激振力及力矩分析结果,进一步定量比较轴向振动位移和径向振动位移频谱中工频及倍频幅值随不同心量变化规律,如图18、图19所示。
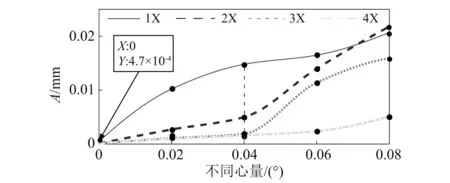
图18 轴向振动位移工频及倍频幅值随不同心量的变化Fig.18 Rotation and its harmonic frequency of axial displacement vibration varied with misalignment values
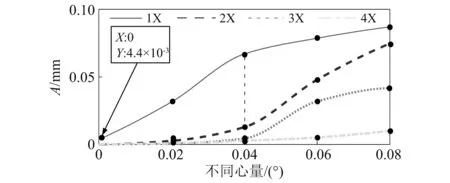
图19 径向振动位移工频及倍频幅值随不同心量的变化Fig.19 Rotation and its harmonic frequency of radial displacement vibration varied with misalignment values
(1) 当高压转子系统仅存在不平衡激励时,轴向振动位移工频及倍频幅值几乎为0,径向振动位移则具有相对较明显的工频振动。
(2) 当存在不同心激励时,轴向振动开始表现出明显的工频及倍频成分,且轴向与径向振动位移的工频及其倍频成分随着不同心量的增加而增加。说明轴向振动工频及倍频是不同心故障的典型特征。
(3) 当不同心量在0°~0.04°内增大时,轴向和径向以工频振动为主,倍频成分虽有增大但增速较小。当不同心量大于0.04°后,工频幅值增速放缓,2倍频、3倍频迅速增大,2倍频幅值可接近甚至超过工频幅值。说明轴向和径向2倍频、3倍频也是不同心故障的典型特征,相对工频幅值的大小可表征不同心故障的严重程度。
在王美令研究中利用单盘转子试验台通过施加垫片来人为制造支承不同心,在不同心响应结果中同样出现了工频及其倍频响应,如图20、图21所示。文献中的结果与本文结果具有一定的相似性;但由于模拟方式的影响、转子系统的差异及对实际支承结构的简化,本文定量分析结果与实际发动机转子系统必定存在一定差异,不过所得的振动特征相对变化特点及规律性结果可为不同心故障诊断提供参考。
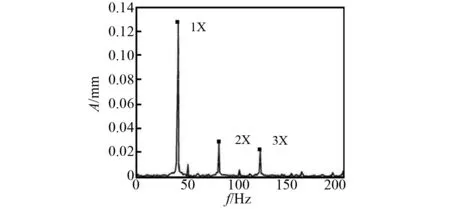
图20 转子轴向振动位移频谱图Fig.20 Axial vibration displacement spectrum of rotor

图21 转子径向振动位移的频谱图Fig.21 Radial vibration displacement spectrum of rotor
3 结 论
本文以某型航空发动机高压转子-轴承支承系统为研究对象,提出基于多体非线性接触动力学的支承不同心故障模拟方法,分析了单个滚珠、滚珠与外圈、外圈与柔性支承的瞬态接触力、力矩以及柔性支承上测点的时频域响应规律,得出如下结论:
(1) 压紧区、松脱区以及单个滚动体与内外圈的相对位置变化产生的复杂相互作用是滚动体接触力复杂频率成分产生的直接原因。
(2) 通过滚珠-轴承外圈-支承间受力及力矩的传递规律与分析发现,全部滚珠与外圈的瞬态接触力合力及合力矩是产生不同心故障特征的激励源。其中,轴向力、力矩及径向力矩频谱中包含明显的工频及倍频成分,径向力主要为工频成分,倍频成分不明显。
(3) 支承测点响应是各个方向力和力矩的综合激励结果。轴向振动工频及倍频是不同心故障的典型特征。轴向和径向2倍频、3倍频相对工频幅值的大小可表征不同心故障的严重程度。
