SMA-负刚度双曲面隔震装置的减震性能研究
2021-06-03杨大余常化慧曹飒飒
杨大余, 常化慧, 曹飒飒
(1. 中交第一公路勘察设计研究院有限公司,西安 710075; 2. 广州大学 土木工程学院,广州 510006)
对于减隔震设计的桥梁结构体系,其基本周期远离地震动的卓越周期,结构内力响应相应于延性桥梁结构体系明显降低。但是,近年来的地震考验表明,减隔震桥梁的限位能力不足,仍然出现大量的碰撞、支座移位或落梁等震害[1-2]。
为提高减隔震桥梁的限位能力和自复位能力,形状记忆合金材料(shape memory alloy, SMA)被引入到减隔震桥梁中。SMA构件与减隔震支座一起,形成新型减隔震装置,可有效减小桥梁结构的最大位移和残余位移,提高其自复位性能[3-9]。但是,引入的SMA限位体系又反过来增大了隔震装置的刚度,一定程度上又增大了桥梁下部结构的内力响应。如何在提高自恢复能力的同时,又不过大增加桥梁下部结构的内力,成为需要解决的一个新问题。
为减小SMA的内力,曹飒飒等[10]提出多级设防的SMA铅芯支座,可以一定程度的降低中、强震作用下的结构内力;Han等[11]提出变曲率的SMA摩擦摆支座,通过减小大位移时的曲率,巧妙的减小了结构的内力响应。上述两种方法的核心思想是减小支座在大位移时的刚度。主动和半主动的隔震装置可以同时减小结构的内力和位移响应[12-14],但是这些装置或多或少的依赖于外部电力控制,而电力供应设施在地震时很容易被破坏。有研究表明[15-17],在某些主动和半主动控制的结构中,控制装置的力-位移关系表现出负刚度特征。
基于这一现象,Iemura等[18]提出一种新型负刚度装置,将该装置与普通橡胶支座并联组成新的隔震系统后,可以大幅减小结构的位移和加速度响应。Attary等[19]模拟分析了安装有负刚度装置的公路桥梁结构,结果表明:该装置不仅可以保持结构稳定,还可以大大减小结构刚度。随后,Attray等[20]对一种新型的负刚度装置进行了振动台试验,证实了在减小结构响应方面,负刚度系统明显优于正刚度系统。在国内,熊世树等[21]通过框架结构振动台试验,验证了负刚度混合隔震系统可以有效减小结构的地震动响应。Sun等[22]提出一种由弹簧、滚轴和滑动轨道组成的负刚度装置,并通过实验验证了其在减小结构地震动响应方面的积极作用。此外,基于预压弹簧、球铰和斜向转动的阻尼器,杨巧荣等[23]提出一种附带阻尼的负刚度装置。该装置不仅能够减小长短周期地震作用下上部结构的加速度响应,还可以控制隔震层的位移响应,提升隔震效率。Liu等[24]将负刚度装置与SMA丝相结合,提出一种可恢复的负刚度系统。他们指出,负刚度装置可以有效的增大结构体系的阻尼比和耗能能力,从而显著减小结构内力。
基于上述研究,本文拟提出一种新型SMA-负刚度双曲面隔震装置。首先,从理论上分析SMA-负刚度双曲面隔震装置的恢复力模型;其次,基于有限元模型,对影响SMA-负刚度双曲面隔震装置的关键参数进行分析;最后,以某连续梁桥为工程实例,验证SMA-负刚度双曲面隔震装置的优越性。
1 SMA-负刚度双曲面隔震装置
1.1 设计原理
SMA索与传统隔震支座组合的隔震系统虽然可以有效提高结构的自复位能力,但是另一方面也增大了结构的内力响应。为了在提供自恢复能力的基础上,同时部分减小结构内力响应,拟基于负刚度设计理念,提出一种新型的SMA-负刚度双曲面隔震装置。其设计理念如图1所示。k1为SMA索体系提供的正刚度,-k2为反双曲面支座提供的负刚度。一方面,将负刚度装置加入SMA隔震体系后,结构的位移响应明显降低;另一方面,负刚度效应将减小隔震装置的整体刚度,从而部分减小结构的内力响应。
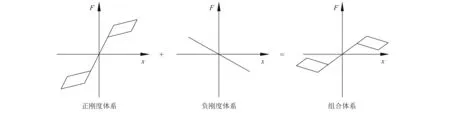
图1 SMA-负刚度双曲面隔震装置的设计原理Fig.1 Design principle of SMA-based negative stiffness isolation bearing
1.2 支座构造
SMA-负刚度双曲面隔震装置由SMA索、上、下凸面钢板和双凹面滑块组成,如图2所示,其剖面如图3(a)所示。SMA索穿过上、下钢板凹槽,在支座的某一侧面进行连接,形成环形布置。SMA索放置于上、下钢板的沟槽内,与钢板接触而不固定,允许索与钢板间发生自由滑动。纵、横向沟槽深度不同,以确保SMA索不接触(见图3(b))。
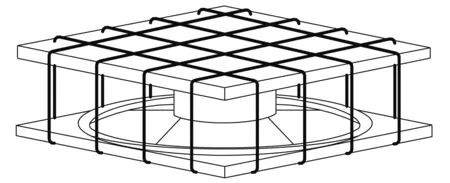
图2 SMA-负刚度双曲面隔震装置Fig.2 SMA-based negative stiffness isolation bearing
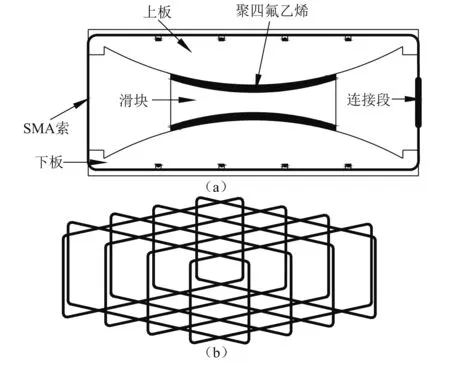
图3 剖面图和SMA索的布置Fig.3 Sectional-view and layout of SMA cables
1.3 作用机制
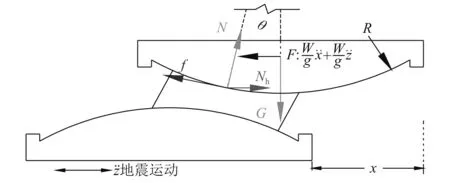
图4 地震作用下负刚度装置受力分析图Fig.4 Free body diagram of a SMA-based negative stiffness isolation bearing
Iemura等指出,地震作用下负刚度装置运动方程为
x=2Rsinθ
(1)
(2)
(3)
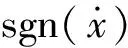
(4)
式中,Nh表达式为
Nh=Gsinθcosθ
(5)
为简化计算,图5中对SMA-负刚度双曲面隔震装置的部分构件作了简化。y为上钢板竖向的位移;L0和L分别为SMA索竖向段的初始长度和拉伸后长度;α为拉索变形后与底板的夹角。
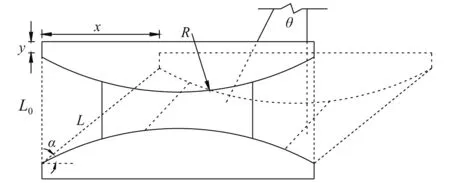
图5 SMA-负刚度双曲面隔震装置计算简图Fig.5 Simplified computing model of a SMA-based negative stiffness isolation bearing
x和y分别表示装置运动的水平和竖向位移,则
y=R(1-cosθ)
(6)
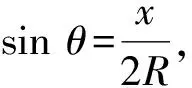
(7)
拉伸的SMA为
(8)
SMA索伸长量ΔL为
(9)
SMA索的应变值为
(10)
则SMA索的恢复力为
FSMA=nAσ(ε)
(11)
式中:n为SMA索的竖向段数目;A为每根SMA索截面面积;σ(ε)为SMA索应力。先根据式(10)求得ε,再由SMA的本构关系求得σ。
水平
(12)
竖向
(13)
式中,α可表示为
负刚度双曲面减震装置水平方向总恢复力为SMA体系水平分力与负刚度体系水平分力之和,根据式(4)、式(5)和式(12)可得
(14)
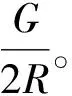
2 SMA-负刚度双曲面隔震装置滞回性能
2.1 试件设计
设计某SMA-负刚度双曲面隔震装置,如图6所示。其边长为0.76 m,高0.2 m。纵、横向均设3条超弹性SMA索,分别放置于纵、横向的沟槽内。纵、横向沟槽深度不同,以避免两个方向的索交叉。上、下反曲面半径均取为1.5 m。圆形滑块半径为0.35 m。上、下钢板和滑块采用Q345钢,其弹性模量为200 000 MPa,泊松比为0.3。滑块及上、下钢板间的滑动摩擦材料采用聚四氟乙烯。上、下钢板通过螺栓分别与主梁、桥墩连接。
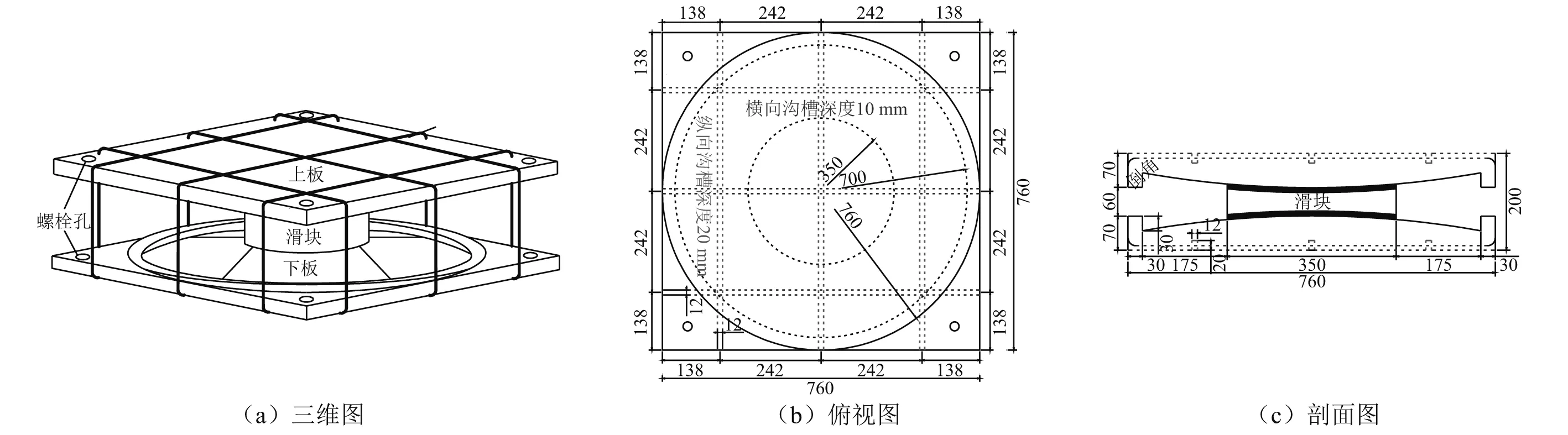
图6 某SMA-负刚度双曲面隔震装置Fig.6 A SMA-based negative stiffness isolation bearing
SMA-负刚度双曲面隔震装置通过超弹性SMA索提供自复位能力。拟设计装置选用美国Fort Wayne公司生产的7×7×0.885 mm的超弹性NiTi SMA索(见图7)。Ozbulut等[25]测试了同一类型索的应力应变关系。为了计算方便,根据他们的试验结果,参考Auricchio等[26]的本构模型,将SMA材料的应力应变模型简化为如图8中虚线所示的旗帜形[27]。

图7 超弹NiTi SMA索Fig.7 Superelastic NiTi SMA cables

图8 SMA索应力与应变关系Fig.8 The stress-strain relationship of SMA cables
2.2 数值模拟
基于ANSYS软件,建立该SMA-负刚度双曲面隔震装置的有限元模型,如图9所示。其中上、下钢板及滑块采用185单元模拟。如要精确模拟环向布置的SMA索的变形行为,需要同时考虑SMA索的材料非线性、几何非线性、大变形效应和索与上、下钢板之间的接触非线性,难度较高。为降低计算难度和减小计算量,采用简化的方法模拟SMA索。将环向布置的SMA索简化为与上、下钢板连接的直索(见图9)。简化原则为:一方面要求简化前后SMA索的有效截面积相同;另一方面根据直线索段长度半环形索与之比,将SMA的弹性模量和强度按比例缩小,以确保SMA体系在横向的恢复力-位移关系相同。SMA索采用ANSYS的186单元和内建的形状记忆合金材料模拟,轴向应力和应变关系的模拟效果如图8所示。
图9 SMA-负刚度双曲面隔震装置的有限元模型Fig.9 Finite element model of SMA-based negative stiffness isolation bearing
下板底面采用固定约束。水平位移加载前,在上板顶面施加竖向压力。为了使装置顶板在运动过程与底板保持水平关系,上板顶面节点Y向自由度建立集中耦合,Z向位移固定,X向施加往复水平位移荷载。滑块与曲面间摩擦因数取为0.02。
为了查验负刚度装置作用的效果,选取曲面半径为2 m的SMA-负刚度双曲面隔震装置。施加竖向荷载1 000 kN,在往复45 mm幅值的水平位移荷载作用下,负刚度双曲面隔震装置、SMA索和SMA-负刚度双曲面隔震装置在水平方向的恢复力-位移滞回曲线比较,如图10所示。由图可知,SMA体系显示出明显的刚度增长,而负刚度双曲面隔震装置显示出明显的负刚度特点,可有效的减小整体隔震装置的正刚度。
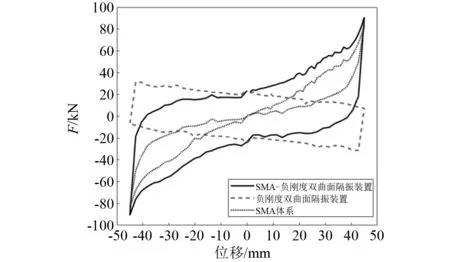
图10 SMA体系、负刚度双曲面隔震装置和SMA-负刚度双曲面隔震装置的滞回曲线Fig.10 Comparison of hysteretic curves of SMA-cable system, negative stiffness isolation bearing system and SMA-based negative stiffness isolation bearing system
2.3 参数分析
为探明各关键设计参数对SMA-负刚度双曲面隔震装置的影响规律,选取不同的关键设计参数,对其力学行为进行比较研究。所选取的关键设计参数有:曲面半径R、水平位移幅值、SMA索截面积、竖向荷载和双曲面形状。为了便于分析讨论,参考文献[28],以水平恢复力-位移曲线上单个滞回环面积作为隔震装置消耗的能量W,并定义等效割线刚度K和等效阻尼比ξ为
(15)
式中:Pmax和Pmin分别为一个加卸载循环的最大和最小剪力; Δmax和Δmin分别为一个加卸载循环的最大和最小位移。
(16)
式中, Δ为一个加卸载循环的位移幅值。
2.3.1 力学性能随曲面半径R的变化规律
选取竖向荷载为1 000 kN。当水平位移幅值为45 mm时,SMA-负刚度双曲面隔震装置在不同曲面半径R下的力学性能,如图11所示,各关键力学参数对比如表1所示。由图11和表1可知,负刚度曲面半径R越小,负刚度装置产生的负刚度就越大,恢复力就越小,这表明结构内力响应随曲面半径的减小而减小。在支座设计时,在条件允许的情况下,可以通过调整曲面半径,实现对隔震装置的刚度优化。在耗能能力和阻尼比方面,曲面半径的影响较小。
2.3.2 力学性能随水平位移的变化规律
选取竖向荷载为1 000 kN。SMA-负刚度双曲面隔震装置在不同水平位移下的力学性能,如图12所示。由图12可知,SMA-负刚度双曲面隔震装置的刚度逐渐增大,可以满足不同地震作用下的抗震性能需求。中小震时隔震效率高,强震时限位效果好。

图11 SMA-负刚度双曲面隔震装置不同曲面半径时的滞回曲线Fig.11 Force-displacement relationships of SMA-based negative stiffness isolation bearings with various radius of curved surfaces

表1 不同曲面半径隔震装置的关键力学参数Tab.1 Key parameters of negative stiffness isolation bearings with different radius of curved surface
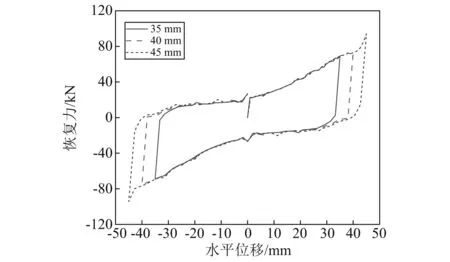
图12 SMA-负刚度双曲面隔震装置不同水平位移时的滞回曲线Fig.12 Force-displacement relationships of SMA-based negative stiffness isolation bearings with various lateral displacements
2.3.3 力学性能随SMA索截面积的变化规律
选取竖向荷载为1 000 kN。SMA-负刚度双曲面隔震装置随不同SMA索截面积的力学性能,如图13所示。当分别采用4根、6根和8根SMA索时,隔震装置的各关键力学参数对比如表2所示。由表2可知,随SMA索截面积的增大,一方面装置剪切刚度增大,限位能力增强;另一方面结构的内力响应增大。随SMA索用量的增加,隔震装置单位循环耗能能力增强。这一方面得益于SMA材料旗帜形本构的附加阻尼;另一方面是因为索竖向分力的增加,导致支座摩擦面的耗能能力增加。
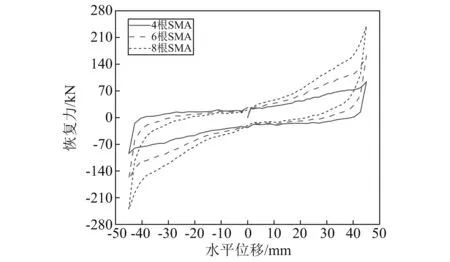
图13 SMA-负刚度双曲面隔震装置不同SMA根数时的滞回曲线Fig.13 Force-displacement relationships of SMA-based negative stiffness isolation bearings with incremental SMA cables

表2 不同索截面尺寸隔震装置的关键力学参数Tab.2 Key parameters of negative stiffness isolation bearings with different section area of SMA cables
2.3.4 力学性能随竖向压力的变化规律
为了研究SMA-负刚度双曲面隔震装置在不同竖向压力G下的力学性能,分别选取竖向荷载700 kN,1 000 kN和1 300 kN进行分析。当水平位移幅值为45 mm时,装置的力学行为如图14所示。竖向荷载分别700 kN,1 000 kN和1 300 kN时,其单位循环所消耗的能量分别为7 243.2 J,8 123.1 J和9 925.3 J,阻尼比分别为27.6%,30.5%和36.3%。由此可知,竖向压力G越大,滞回曲线面积也越大,SMA-负刚度双曲面隔震装置耗能能力越强。
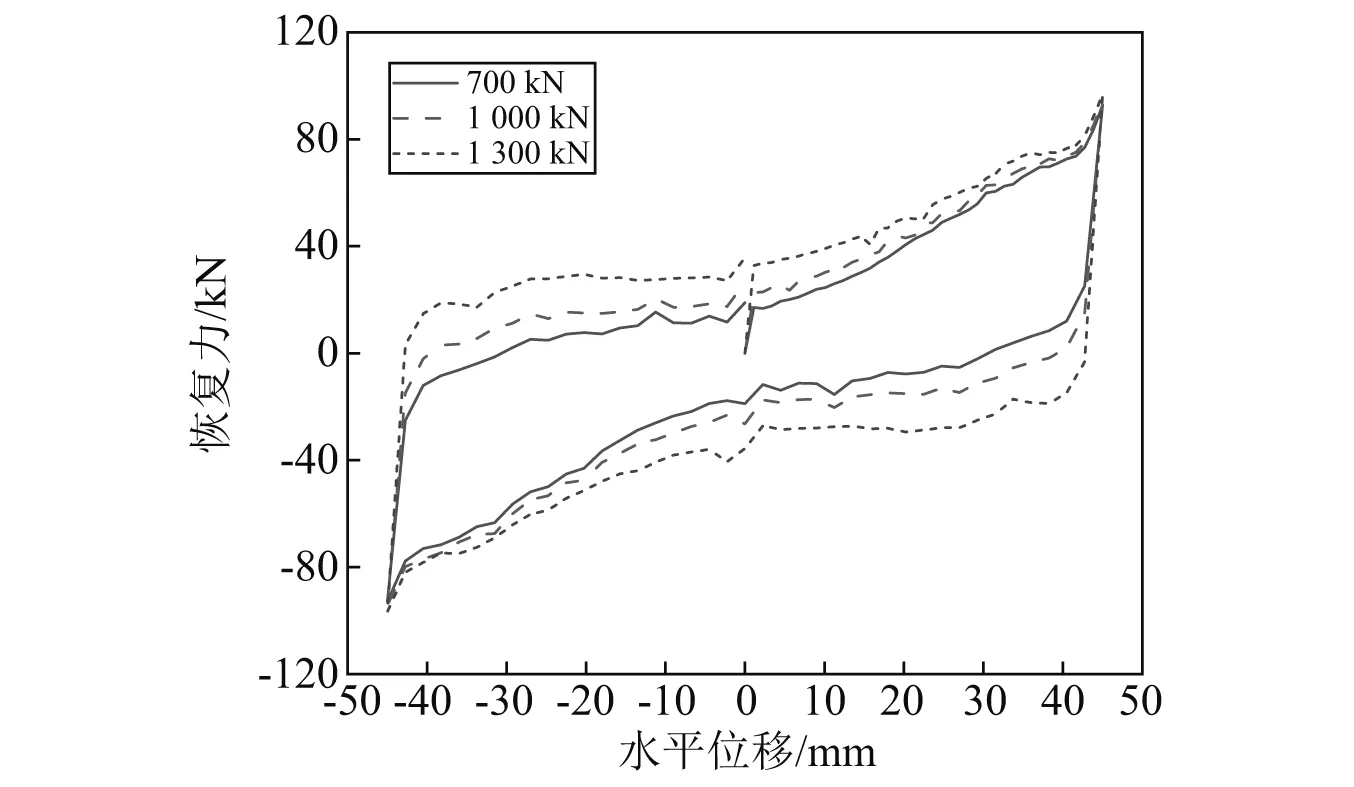
图14 SMA-负刚度双曲面隔震装置不同竖向压力时的滞回曲线Fig.14 Force-displacement relationships of SMA-based negative stiffness isolation bearings with various axial forces
2.3.5 双曲面形状对力学性能的影响
为了进一步研究不同曲面形状对隔震装置刚度的影响,选取1.5 m半径的正、负刚度曲面和零刚度的平面进行研究。选取竖向荷载为1 000 kN。当水平位移幅值为45 mm时,三种减震装置的恢复力和位移曲线如图15所示,关键力学参数如表3所示。由图15和表3可以明显看出三种曲面对装置刚度的影响。三种曲面所产生的支座刚度从小到大依次为负刚度曲面、平面、正刚度曲面。与SMA正刚度双曲面减震装置相比,SMA-负刚度双曲面隔震装置等效割线刚度减小36.8%,可以有效降低结构的内力响应。
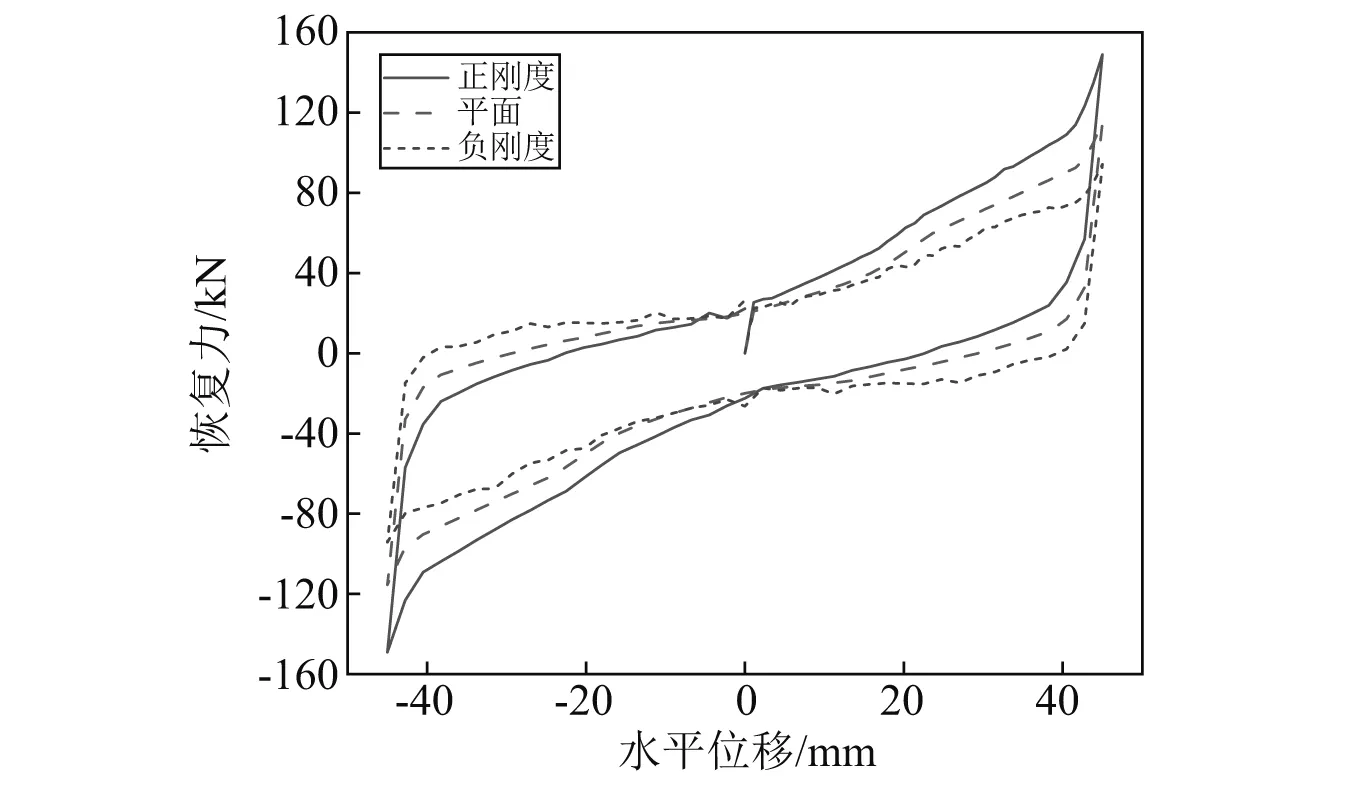
图15 SMA正刚度、平面、负刚度减震装置滞回曲线Fig.15 Force-displacement relationships of SMA-based positive, zero and negative stiffness isolation bearings

表3 不同曲面形状隔震装置的关键力学参数Tab.3 Key parameters of negative stiffness isolation bearings with different shapes of curved surface
3 减震性能分析
某4×30 m 预应力混凝土连续梁桥的SAP2000有限元模型,如图 16所示。主梁截面为单箱多室(见图17)。双柱式桥墩,桥墩中间设一道系梁。桥台高2.5 m,每个桥台下设4根灌注桩。主梁采用 C50 混凝土,桩基、桥台和系梁采用 C30 混凝土。为了对比分析不同支座的影响,分别对不设SMA索的摩擦摆支座和设置SMA索的正刚度、零刚度和负刚度SMA双曲面减震装置进行抗震分析。摩擦摆支座、正刚度和负刚度SMA隔震支座的曲面半径为1.5 m,零刚度采用平面。考虑到主梁质量较大,SMA索的长度和截面积均较2.1部分增大2倍。
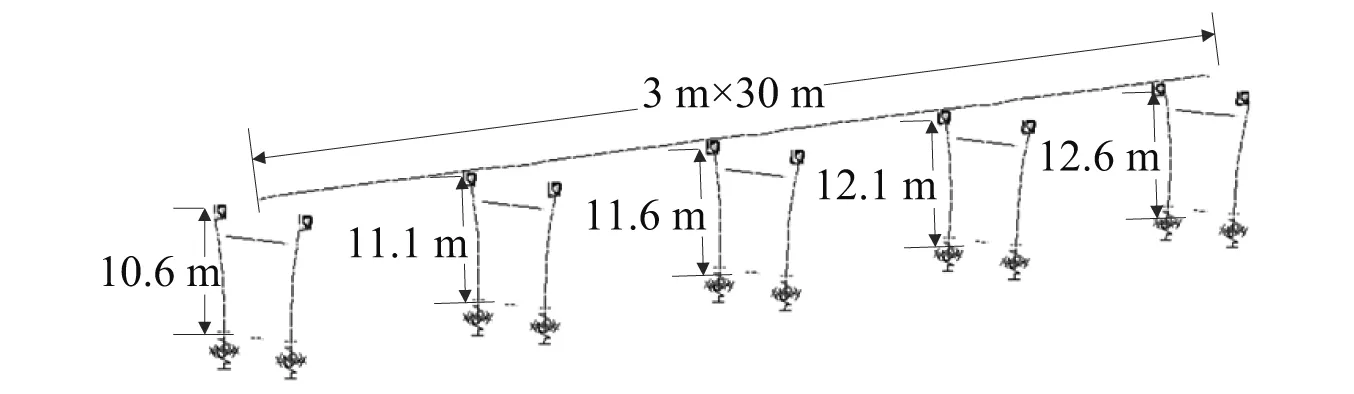
图16 某连续梁桥Fig.16 A continuous girder bridge
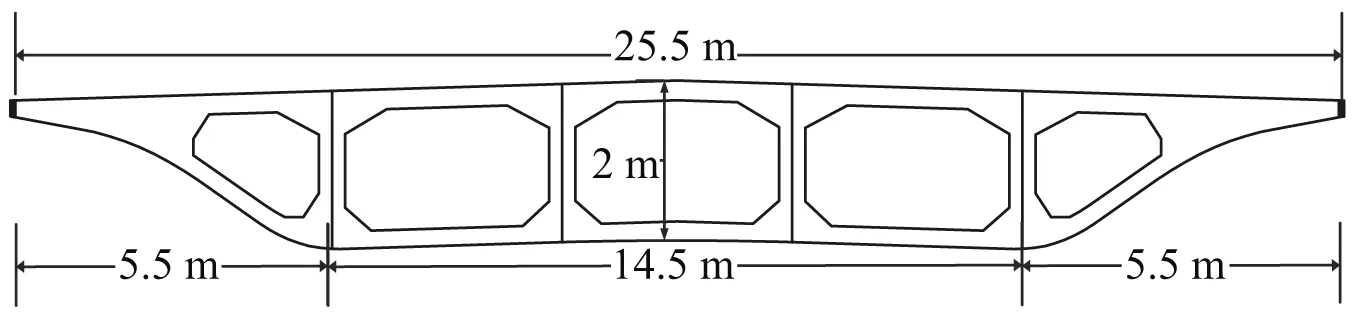
图17 主梁截面示意图Fig.17 Cross section of the girder of the continuous bridge
3.1 有限元模拟
基于SAP2000软件建立全桥的有限元模型。主梁、桥墩采用弹性的框架单元模拟。桩-土相互作用采用3个转动、3个平动的六弹簧单元模拟。因本桥为混凝土结构,阻尼比取为0.05。
SMA索体系采用多段线弹性单元和多段塑性单元并联模拟(见图18)。两种连接单元的组合方法为同一位移处的恢复力叠加。负刚度双曲面隔震装置部分采用Plastic(Wen)单元和斜率为负的线性连接单元模拟;平面减震装置采用Plastic(Wen)模拟;正刚度双曲面隔震装置采用Plastic(Wen)和斜率为正的线单元模拟。
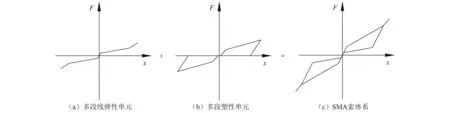
图18 SMA索体系水平剪力-位移关系Fig.18 Lateral force-displacement relationship of SMA-cable system
为了验证减震装置在SAP2000软件中模拟的正确性,图19对比了SAP2000和ANSYS两种软件模拟减震装置所得的滞回曲线。总体来看,两种软件对减震装置计算的恢复力模型基本一致,这说明SAP2000可以很好的模拟减震装置的本构关系。
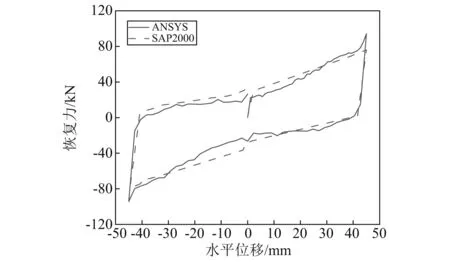
图19 SMA负刚度隔震装置的恢复力-位移关系Fig.19 The force-displacement relationships of SMA-based negative stiffness isolation bearings
3.2 地震波
根据地震安全性评价报告,该桥的基本设防烈度为7度, Ⅱ类场地。从PEER地震数据库选取单一方向分量的3条近场地震波。根据该桥梁所在场地的设计反应谱,基于SeismoMatch软件,对所选的3条地震波进行缩放[29]。3条缩放后地震波的反应谱和设计反应谱对比,如图20所示。将缩放后的地震波作为时程分析的地震波,沿纵桥向输入。本文中的时程分析结果均为纵桥向响应。
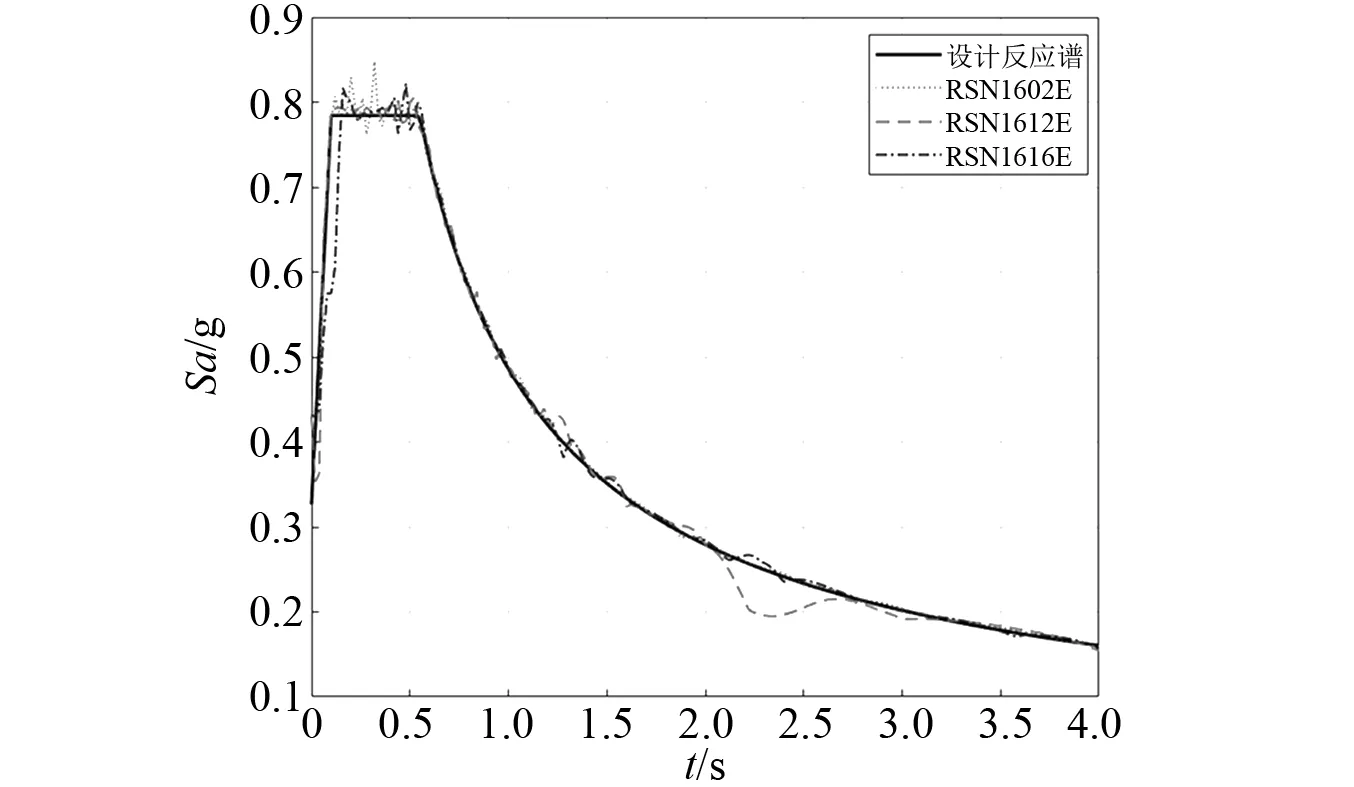
图20 近场地震波Fig.20 Near-fault earthquake accelerograms
3.3 地震响应对比分析
3.3.1 支座位移响应
在三种近场地震动作用下,对于分别采用摩擦摆支座、正刚度、零刚度和负刚度SMA隔震支座的桥梁结构体系,中间墩右侧支座的位移历程曲线如图21所示,支座最大位移如表4所示。
由图21可以看出,在近场地震动作用下,正刚度、零刚度和负刚度SMA隔震装置均能较好的控制支座位移。由表4可知,虽然SMA-负刚度双曲面隔震桥梁的支座位移略大于SMA平面隔震桥梁和SMA正刚度双曲面隔震桥梁;但是和负刚度与普通摩擦摆隔震支座的位移相比,负刚度支座的位移并未增大很多。这表明相对于常用的正刚度SMA隔震装置,采用负刚度理念设计的SMA隔震装置并不会造成过大的位移增长。此外,在RSN1612E地震动作用下,采用传统摩擦摆支座的桥梁体系存在约0.006 m的残余位移,而在SMA辅助的正刚度、零刚度和负刚度隔震桥梁体系中均未发生,这表明它们都具有较好的自复位能力。

图21 近场地震动作用下支座位移时程曲线Fig.21 Displacement time-histories of isolation bearings under near-fault earthquakes
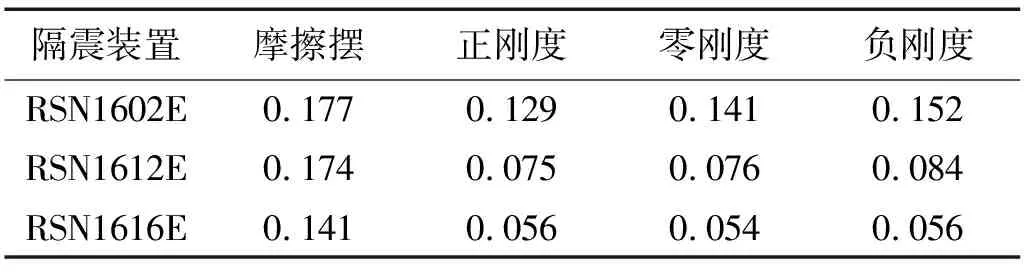
表4 四种隔震桥梁的最大支座位移比较Tab.4 Comparison of maximum bearing displacements of the bridge isolated by four different types of isolator
3.3.2 支座滞回曲线
在三种近场地震动作用下,对分别采用摩擦摆支座、正刚度、零刚度和负刚度SMA隔震支座的桥梁结构体系,中间墩右侧的支座滞回曲线如图22所示。
由图22可知,正刚度、零刚度和负刚度SMA双曲面隔震装置均在近场地震动作用下可有效限制支座的位移。其中,SMA-负刚度双曲面隔震装置支座剪力最小,SMA平面减震装置支座剪力稍大,SMA正刚度双曲面减震装置支座剪力最大。与SMA正刚度相比,SMA负刚度支座的剪力普遍降低,这充分体现了负刚度设计理念的优越性。在RSN1602E地震波作用下,SMA零刚度和负刚度隔震装置的SMA索轻微进入奥氏体强化阶段,可提供与正刚度SMA双曲面隔震装置相类似的限位能力。

图22 近场地震动作用下支座剪力时程曲线Fig.22 Shear force time-histories of piers under near-fault earthquakes
3.3.3 承台底剪力响应
三种近场地震动作用下,四种隔震桥梁结构体系的中间墩右承台底的剪力历程曲线,如图23所示。为显示清楚,截取了波峰和波谷处的部分历程曲线。
由图23可以看出,在近场地震动作用下,正刚度、零刚度和负刚度SMA隔震桥梁结构体系的承台底剪力均比传统摩擦摆支座大。SMA正刚度双曲面隔震桥梁体系产生的承台底剪力最大,其次为SMA平面隔震桥梁体系,而SMA-负刚度双曲面隔震桥梁体系的承台底剪力最小。以中间墩右侧承台底最大剪力为例,与采用摩擦摆支座的桥梁结构体系相比, SMA-正刚度隔震桥梁体系的剪力在三种地震动下依次分别增长55.2%,38.2%和28.1%;而与SMA-正刚度隔震桥梁结构体系相比, SMA-负刚度隔震桥梁体系的剪力在三种地震动下依次分别减小8.4%,9.5%和7.3%。这表明,SMA体系加入摩擦摆支座后,会造成结构内力的显著增加;而引入负刚度理念的SMA-负刚度双曲面隔震装置,可以部分减小传递至基础的地震动内力响应。
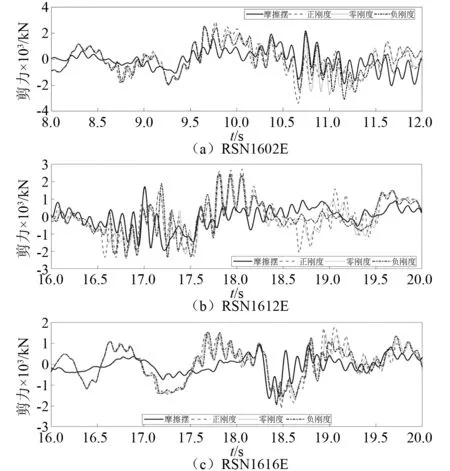
图23 近场地震动作用下承台底弯矩时程曲线Fig.23 Bending moment time-histories of caps under near-fault earthquakes
4 结 论
(1) SMA-负刚度双曲面隔震装置可以为桥梁提供自复位能力。与传统摩擦摆支座相比较,SMA-负刚度双曲面隔震装置可以显著减小桥梁结构的墩梁间相互位移;与SMA-正刚度双曲面隔震装置相比,SMA-负刚度双曲面隔震装置可以减小支座等效割线刚度,增大阻尼比和耗能能力,从而部分减小下部结构的内力响应。
(2)随支座位移的增大,SMA-负刚度双曲面隔震装置的等效割线刚度显著增大,具有较好的强震限位能力。
(3) SMA-负刚度双曲面隔震装置的负刚度的大小取决于曲面半径。曲面半径越小,负刚度效应越大。可以通过调整曲面半径,实现对隔震装置的刚度优化。
(4) 随SMA索截面积的增大,虽然SMA-负刚度双曲面隔震装置的等效割线刚度增大,耗能能力和限位能力增强,但是这也会使得结构的内力响应增大。随竖向荷载的增大,SMA-负刚度双曲面隔震装置的耗能能力增大。
