用于纹理辨识的磁致伸缩触觉传感器研究

赵智忠，索 峰，万丽丽，王博文

(河北工业大学，省部共建电工装备可靠性与智能化国家重点实验室，河北省电磁场与电器可靠性重点实验室，天津 300130)

0 引言

当前机器手已成为科研和生活的热点话题，触觉传感器作为机器手的重要组成部分得到了广泛的关注[1]。触觉传感器可以通过检测物体压力[2]、形状[3]、振动[4]、温度[5]等信息来辅助机器手对物体进行识别。但是目前安装在机器手上的触觉传感器还达不到对物体的表面纹理结构的准确辨识。因此，设计可以准确辨识物体表面纹理信息的触觉传感器，对机器手对于物体的识别有重要的意义。

纹理的准确检测与辨识可以为机器手触觉感知提供重要的帮助。国内外的研究者对纹理触觉传感器做了诸多的工作。文献[6]设计了基于半导体纳米粒子的光学式触觉传感器，通过透射纹理表面得到的应力图像辨识纹理，传感器对于纹理的辨识率可以与人的手指相当。文献[7]设计了可以辨识纹理的光学式触觉传感器GelSight，传感器的灵敏度与分辨率已经超过人手指尖水平。但以上两种光学式触觉传感器都存在体积大的问题，并且对于检测所得到的图像处理也过于复杂。文献[8]利用氧化锌压电丝制作了一种表征纹理间距的压电式触觉传感器。但是这种传感器存在着响应速度慢的问题。文献[9]利用2×2触觉传感器阵列对纹理样本进行检测，将检测结果进行频谱分析并进行对纹理样本的分辨。文献[10]采用液体式触觉传感器进行对日常生活用品纹理的识别。但是这种触觉传感器内部充有液体，为了避免液体泄漏，需要对传感器进行很好的密封，对工艺要求较高，制作成本高。

上述用于纹理辨识的触觉传感器存在着响应速度慢、成本高、对工艺要求高等问题。针对这些问题，本文结合新型磁致伸缩材料铁镓合金(Galfenol)具有机械性能好、响应速度快、成本低等优点[11]，设计了用于纹理辨识的磁致伸缩触觉传感器。根据磁致伸缩逆效应、欧拉-伯努利梁结构动力学理论、磁致伸缩材料线性本构方程、传感器与纹理面接触轨迹等建立触觉传感器输出电压模型。通过提取输出电压峰值与电压信号周期表征物体的纹理属性。并确定传感器工作时最佳偏置磁场值与重复性最低时接触速度大小。

1 触觉传感器结构设计

触觉传感器内部由探针触头、Galfenol材料、霍尔元件、永磁体、硅胶外壳组成，触觉传感器结构如图1所示。Galfenol材料采用取向为<100>的Fe83Ga17片状材料，在此取向下，Fe83Ga17材料具有极高的磁致伸缩性能[12]。Galfenol片状材料长(l)为10 mm、宽(w)为3 mm，厚(h)为0.1 mm。Galfenol材料一端与探针触头相连，另一端固定在传感器外壳上，共同组成悬臂梁结构。探针触头一侧为悬臂梁自由端，固定在传感器外壳一侧为悬臂梁固定端。Galfenol材料两端上方各有一枚永磁体，这两枚永磁体的极性相反，两枚永磁体与Galfenol材料形成闭合磁路，为Galfenol材料提供均匀的偏置磁场。

图1 触觉传感器结构图

触觉传感器的工作原理为：当传感器探针触头划过纹理表面时，探针触头的振动会引起Galfenol材料形状的变化，根据磁致伸缩逆效应，Galfenol材料的磁感应强度会发生变化，霍尔元件将磁场强度的变化转化为电压信号的变化并由信号采集单元输出。

2 触觉传感器的输出模型

传感器的输出电压由霍尔元件检测，霍尔元件检测Galfenol材料表面磁通变化，而Galfenol材料表面磁通变化与内部磁通变化成近似线性关系，可以得到霍尔元件输出电压与Galfenol内部磁通密度的关系：

UH=KHKSB

(1)

式中：UH为霍尔元件输出电压；KH为等效霍尔系数；KS为磁通密度传递系数；B为Galfenol材料内部磁通密度。

触觉传感器选用的霍尔元件型号为SS491B，输出参考电压为2.5 V，为了更好地观察传感器检测纹理时电压信号的变化，利用外电路将其输出参考电压调整为0 V，则传感器输出电压U可以直接表示为

U=UH=KHKSB

(2)

Galfenol磁致伸缩材料的线性本构方程为：

B=dσ+μ0H

(3)

(4)

式中：σ为悬臂梁所受轴向应力；d为磁机耦合压磁系数；μ0为真空磁导率；E为杨氏模量；H为永磁体提供的偏置磁场；ε为悬臂梁长度方向上总应变。

将式(4)带入式(3)得到Galfenol材料的内部磁通密度B为

B=dEε+(μ0-d2E)H

(5)

在图1中，取Galfenol悬臂梁的长度方向为x轴方向、宽度方向为y轴方向、高度方向为z轴方向。对所建立的模型做出以下假设：Galfenol材料悬臂梁为欧拉-伯努利梁；磁场在悬臂梁中沿x轴均匀分布。

由欧拉-伯努利梁结构动力学理论可以得到悬臂梁受力与挠度之间的关系为

(6)

式中：ω为悬臂梁任意一点的挠度；F为施加在探针触头上的力；l为悬臂梁的长度；x为悬臂梁上一点到自由端的距离。

取x=l，得到悬臂梁自由端的挠度与受力关系为

(7)

式中ωf为悬臂梁自由端的挠度值。

将式(7)带入式(6)，可以得到悬臂梁上任意一点挠度与自由端挠度的关系为

(8)

根据材料力学中性层曲率表示公式，x轴上任意一点梁的应变为

(9)

式中：εx为悬臂梁x轴上任意一点应变；z为悬臂梁表面到中性面的垂直距离，为Galfenol材料悬臂梁高度的一半。

对式(9)进行积分，可以得到梁的长度方向总应变为

(10)

根据式(2)、式(5)、式(8)、式(9)、式(10)，可以得到传感器输出电压U与悬臂梁自由端挠度的公式为

(11)

根据式(11)看出传感器输出电压值与悬臂梁自由端挠度有关，悬臂梁自由端挠度反映了悬臂梁振幅的大小，而振幅的大小则由纹理结构而定。传感器在接触微型纹理时需要与纹理表面产生相对滑动，探针触头会在纹理的凸脊上依次划过，这样探针触头在纹理表面滑动的过程中产生的轨迹会形成一个偏移面。如图2所示。

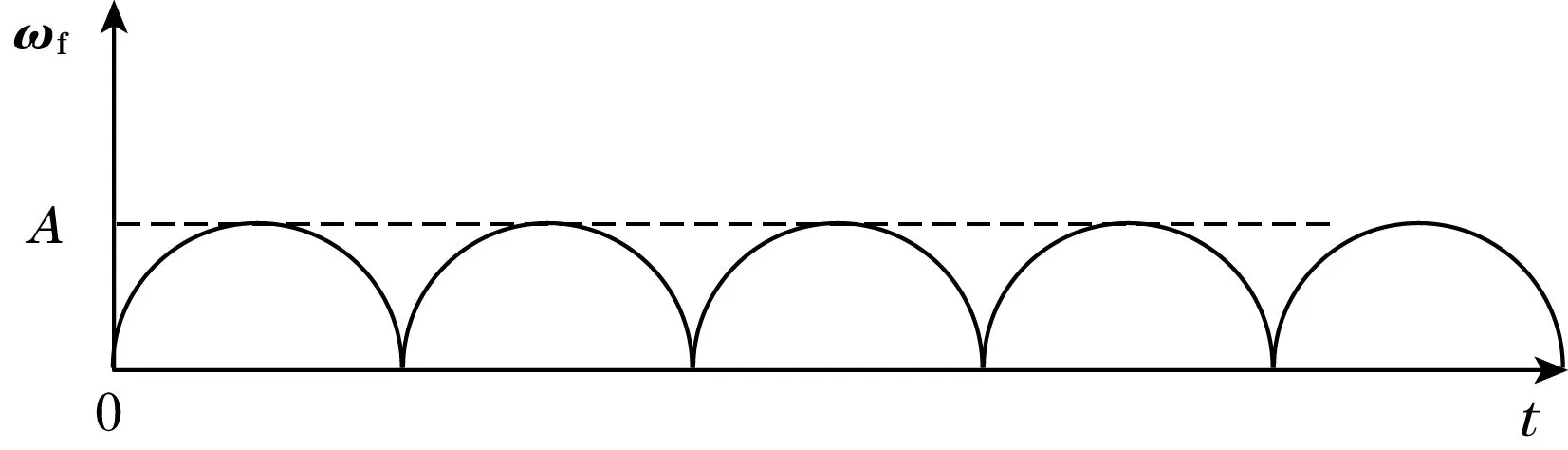
图2 纹理偏移面示意图

在纹理测试中，可以将探针在纹理表面移动的轨迹表示为

(12)

式中：A为纹理高度值；T为探针在划过纹理表面时形成的偏移曲线的周期。

探针触头与纹理表面的接触速度和相邻纹理间距的关系为

(13)

式中：λ为相邻纹理间距；v为探针触头与纹理表面的接触速度。

将式(13)带入式(12)可以得到：

(14)

将式(14)带入式(11)中，可以得到传感器输出电压为

(15)

从式(15)中可以看出，在传感器组成元件及尺寸确定的情况下，确定了传感器与纹理表面接触速度v，则传感器输出电压只与纹理的高度A、纹理的间距λ有关。

3 实验结果与分析

实验平台由机器手、触觉传感器、滑台、电机控制系统、示波器组成，如图3所示。机器手选用的是COBOT机器手，该机器手由双指组成。滑台为ST型电动直线滑台模组导轨，速度在0～5 cm/s可调。在测量纹理时，将纹理表面固定在滑台上，改变电机的转速可以设定纹理面与触觉传感器不同的接触速度。示波器检测触觉传感器的输出电压信号，计算机对输出信号进行处理。纹理检测流程如图4所示。

图3 纹理辨识系统实物图

图4 纹理检测流程图

实验前，需要进行外加偏置磁场测试。偏置磁场会影响传感器的输出特性。模仿人体感受纹理时手指受到力的大小向悬臂梁自由端施加0～2 N的作用力，通过改变永磁体的材料与形状改变偏置磁场大小。5种永磁体提供的偏置磁场分别为1.8、3.2、4.4、5.0、5.3 kA/m。在不同的偏置磁场下传感器受力与输出电压关系如图5所示。

图5 不同偏置磁场下接触力与输出电压关系

测试结果表明，当永磁体提供的偏置磁场强度大于4.4 kA/m时，触觉传感器的输出电压基本不再随偏置磁场的增加而增大。当偏置磁场强度为4.4 kA/m时，触觉传感器的输出与施加在触觉传感器上的力具有很好的线性度，并且传感器的灵敏度也同偏置磁场为5.0 、5.3 kA/m时相当。因此，为了使触觉输出信号明显，具有良好的线性度和灵敏度，本文设计的传感器最佳偏置磁场为4.4 kA/m。

采用3D打印技术打印2组栅状纹理样本，样本的材料为树脂。设计的纹理样本分别从纹理高度值、纹理间距值改变纹理特征。设计的第一组样本保持纹理间距值不变，改变纹理高度值，参数如表1所示。

表1 第一组纹理样本参数值 mm

设计的第二组纹理样本保持纹理高度值不变，改变纹理间距值，参数如表2所示。

表2 第二组纹理样本参数值 mm

对于打印的纹理样本进行实验，设定触觉传感器与被测纹理样本之间的接触速度为2 cm/s，对于表1中各纹理样本分别进行时间为0.2 s的动态接触测试，样本1、3、5测试得到的输出电压随时间变化关系如图6所示。

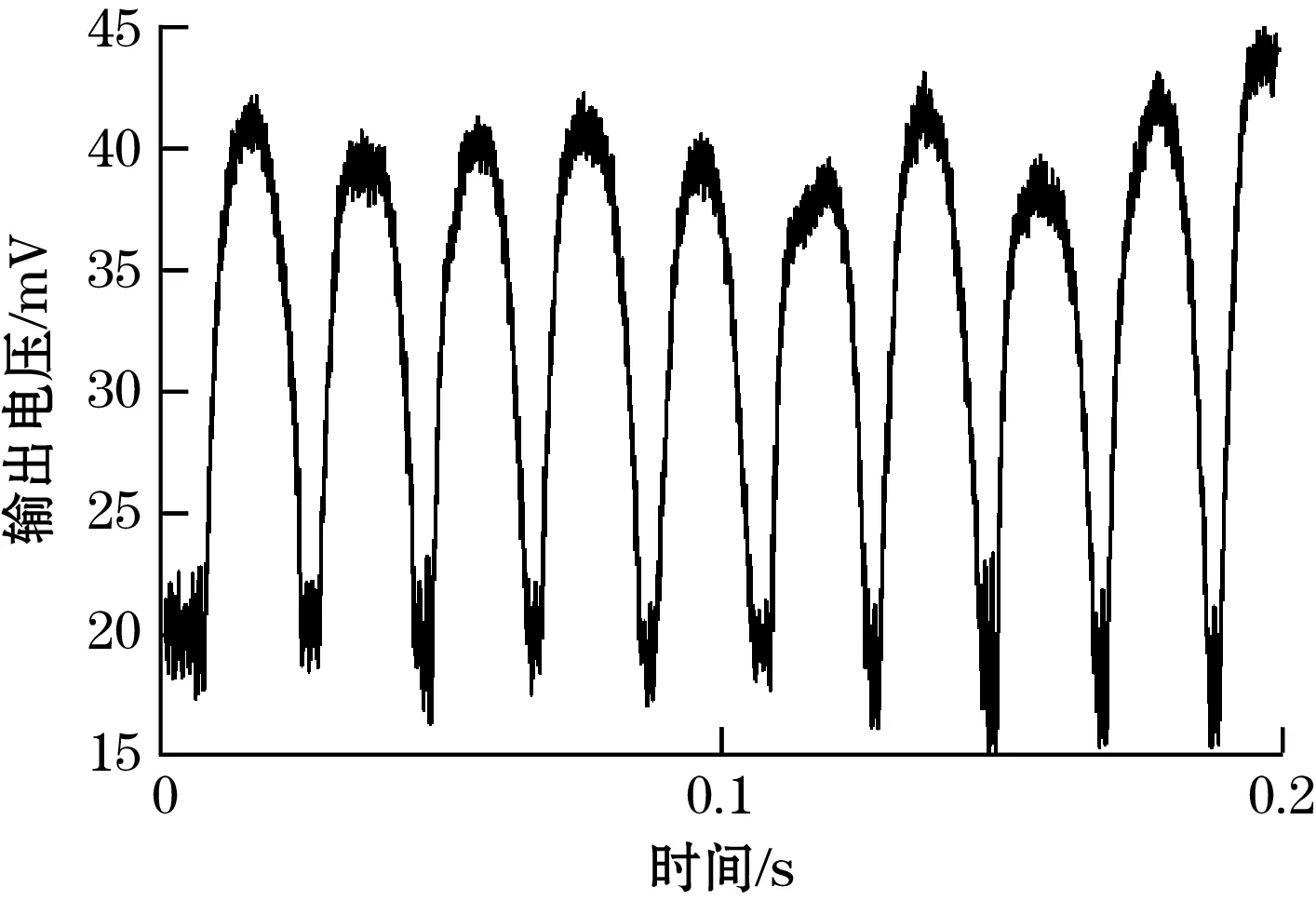
(a)纹理样本1电压波形

(b)纹理样本3电压波形

(c)纹理样本5电压波形图6 传感器对样本1、3、5输出电压实验图

由图6看出在纹理高度增加时，传感器在实验中测得输出电压峰值随之增加。纹理高度与传感器输出峰值电压之间的关系如图7所示。

图7 纹理高度与传感器输出电压峰值关系

由图7可以看出，随着纹理高度值增加，传感器输出电压峰值增加，并且曲线成良好的线性关系。表明可以通过传感器输出电压峰值表征纹理的高度值。

同样对于表2中各纹理样本进行动态接触测试，接触速度为2 cm/s，样本12、13、14在0～0.2 s内得到的输出电压随时间变化关系如图8所示。

(a)纹理样本12电压波形

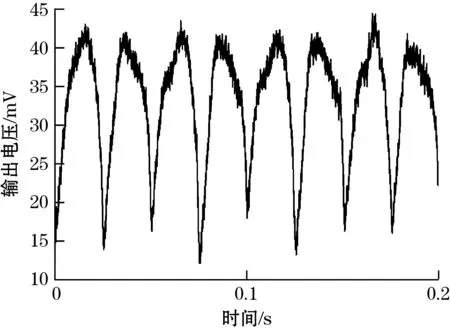
(b)纹理样本13电压波形

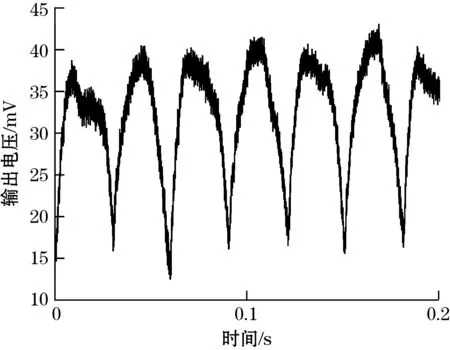
(c)纹理样本14电压波形图8 传感器对样本12、13、14输出电压实验图

由图8可以看出，在纹理高度保持不变时，传感器输出电压峰值基本保持不变，而随着纹理间距的变化，传感器输出电压波形的周期会发生变化。第二组样本输出电压波形周期与纹理间距关系如图9所示。

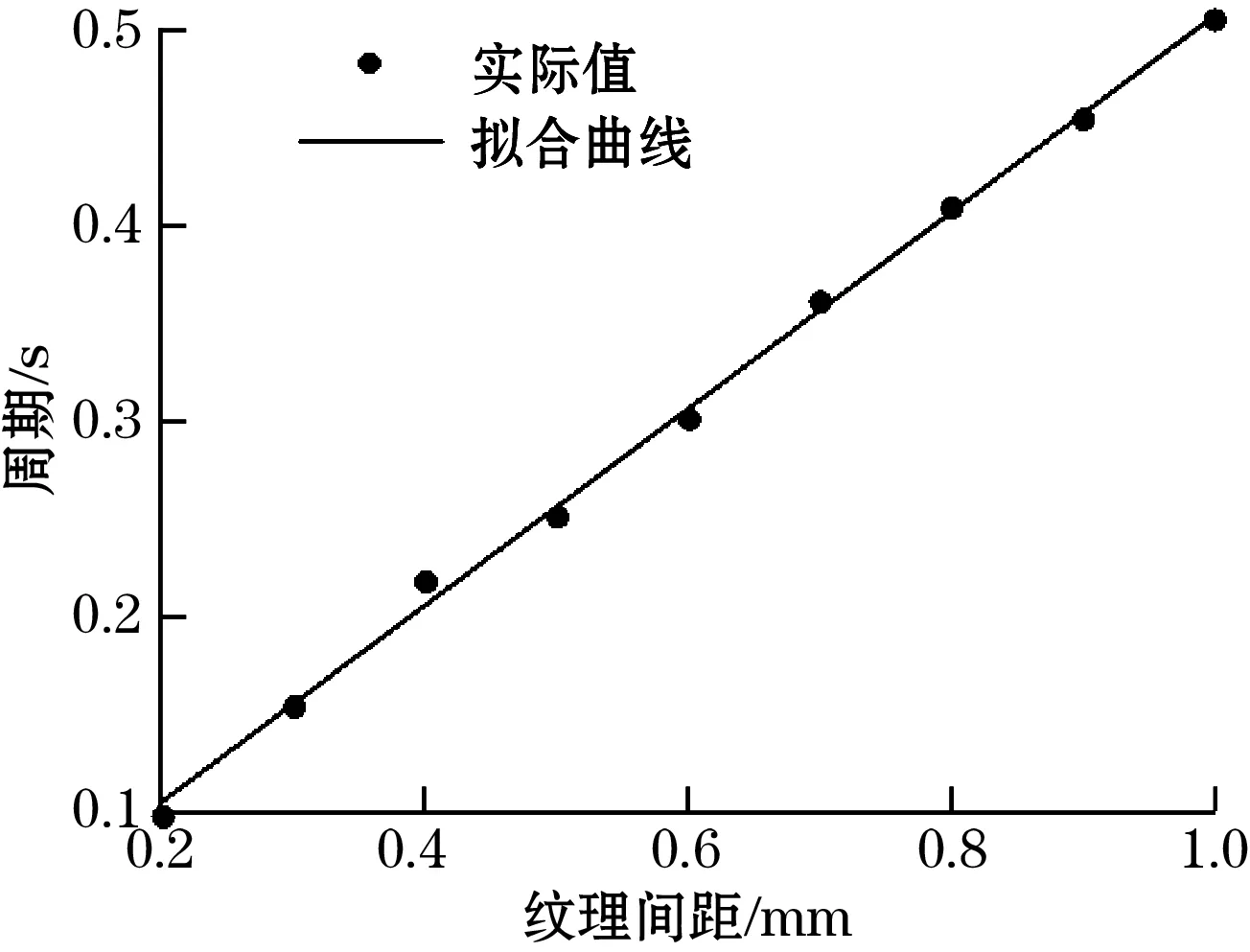
图9 传感器输出电压周期与纹理间距关系

由图9可以看出，随着纹理间距值增加，传感器输出电压周期增加。两者呈近似线性关系。表明可以采用传感器输出电压波形周期表征纹理间距。以此达到辨识不同纹理的要求。

在传感器探测纹理表面时，接触速度将会对实验结果产生影响，为了探究速度对实验的影响，对于样本1进行同方向多次测量，计算传感器的重复性，并探究速度对重复性的影响。重复性指标采用输出最大不重复误差与满量程输出的百分比表示：

(16)

式中：ΔR为输出最大不重复误差；YS为传感器满量程输出。

传感器重复性代表传感器多次测量的误差情况，重复性越小代表传感器多次测量时误差越小。

对于样本1进行在0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0 cm/s速度下的重复性实验，得到重复性与速度关系如图10所示。

图10 接触速度与传感器重复性关系

可以看出在传感器与样本接触速度为0～1.5 cm/s时，传感器重复性在下降，在2.5～4 cm/s时，重复性在上升，在接触速度为1.5～2.5 cm/s时重复性低，并且在接触速度为2 cm/s时传感器重复性达到最低值。这种情况产生的原因为：在接触速度为1.5 cm/s以下时，传感器接触速度较慢，实验受机器手与滑台移动影响大，传感器在多次实验时会产生一定误差。而当接触速度大于2.5 cm/s时，传感器在触觉纹理表面时只会划过纹理表面的凸起部分，这就表示传感器将会无法完全检测到纹理表面结构，因此传感器多次测量将会产生误差，造成重复性下降。因此本传感器使用时最佳接触速度为2 cm/s。

4 结束语

设计并制作了一种用于纹理辨识的磁致伸缩触觉传感器，基于磁致伸缩逆效应、欧拉-伯努利梁结构动力学理论、磁致伸缩材料线性本构方程、传感器与纹理面接触轨迹等建立触觉传感器输出电压模型。确定了传感器最佳偏置磁场为4.4 kA/m。通过对纹理样本检测，将传感器得到的电压信号进行峰值电压与周期提取。峰值电压可以表征纹理的脊高、周期可以表征纹理的间距。表明应用输出电压峰值及输出电压信号周期可辨识纹理结构。通过对不同接触速度对传感器重复性的影响确定了传感器检测时与物体表面的最佳接触速度为2 cm/s。