小口径液体涡轮流量传感器数学模型的研究

2021-06-03郭素娜杨子航

仪表技术与传感器 2021年5期

郭素娜,郑鑫,杨子航,刘旭

(1.河北大学质量技术监督学院，河北保定 071000；2.国家和地方计量仪器与系统联合工程研究中心，河北保定 071000)

0 引言

随着流体力学理论和计算机技术的发展，CFD仿真成为研究传感器内部流场的重要手段。文献[1]利用FLUENT对气体涡轮流量传感器内部流场进行了研究，并用流场的细节解释实验过程中的现象。文献[2]通过CFD仿真预测切向涡轮的叶轮转速，并与实验结果对比。文献[3]基于CFD仿真分析了传感器性能受被测流体黏度变化影响的机理。文献[4]在CFD仿真过程中考虑了机械摩擦力的影响，并建立新的仿真模型。文献[5]提出了一种改进的光纤涡轮流量计。建立了改进型流量计的理论模型。优化后的前导叶片的螺旋角加涡轮的螺旋角等于90°，涡轮的起始体积流量可以达到最小值，灵敏度可以达到最大值，并通过CFD仿真得到了验证。文献[6]利用变温航空润滑油流量标准装置对10支涡轮流量计在多个黏度点下进行校准试验，进一步提出通过关键点雷诺数确定流量选点的校准方法，关键点拟合结果与全数据拟合结果两者差别基本小于±0.33%。

涡轮流量传感器的磁电信号检出器根据电磁感应原理将叶轮的转速转换成了有规律的电信号。文献[7]的研究表明，磁电信号检出器对叶轮产生一个附加阻力矩，但是定量计算此附加阻力矩比较困难。众研究者在建立传感器的数学模型[8-10]时，经常将其忽略不计，或者直接赋予其一个定值。利用这些数学模型对大口径传感器性能进行预测时，由于驱动力矩及各黏性阻力矩较大，而磁阻力矩Tm相对较小，计算过程若忽略磁阻力矩对预测的结果影响不大。但是，对小口径传感器，情况则不同。

本文为考察磁阻力矩Tm大小对小口径传感器性能的影响程度，取一种结构的DN10涡轮流量传感器为研究对象，通过在数学模型中赋予磁阻力矩Tm不同的值对传感器的性能进行预测，并与实验测试进行比较。利用FLUENT软件对传感器内部流场进行仿真，通过流场的信息计算出轴与轴承间的阻力矩Tb和磁阻力矩Tm之和TM，建立适合于小口径涡轮流量传感器的数学模型。

1 涡轮流量传感器实流测试

首先选取4块相同结构10 mm口径液体涡轮流量传感器为实验样机，分别在天津大学流量实验室水流量标准装置上进行实流测试，实验过程采用静态称重法，装置整体的不确定度为0.047 6%(k=2)。依据涡轮流量传感器检定规程，实验测试的流量点为0.2、0.3、0.48、0.84、1.2 m3/h。实验结果如图1所示。

涡轮流量传感器性能受加工精度影响较大，因而相同结构的不同传感器测量结果差别很大。为减小因加工精度带来的测量误差，取4块传感器测试结果的平均值为最终实验结果，如图1中虚线所示。

2 利用数学模型对传感器性能的预测

文献[7]在机翼理论基础上，将黏性边界层理论应用于叶片表面升力系数CL和黏性摩擦阻力系数CD的计算；并对叶片顶端间隙漏流影响和二次流损失所产生的阻力进行计算，建立涡轮流量传感器的黏性数学模型。通过对50 mm口径涡轮流量传感器性能的预测结果与实验数据比较，验证了所建模型的有效性和对传感器特性预测的准确度。

在此，利用文献中的数学模型对10 mm口径涡轮流量传感器性能进行预测，其中Tm分别取0、1、5、10、30 μN·m，预测结果如图2所示。Tm值对传感器性能的影响较大。若在数学模型中对其忽略不计或者任意赋予其某个给定值，将影响对涡轮流量计性能的判定结果。

3 基于CFD仿真求取TM值

3.1 传感器三维仿真模型及网格剖分

根据传感器的实际结构尺寸，用GAMBIT软件建立DN10涡轮流量传感器的三维仿真模型，如图3所示。为了使进口、出口流体流动接近充分发展状态，在前导流件上游和后导流件下游分别增加了5D的前直管段和10D的后直管段。

在剖分网格时，将模型分为7个部分。其中，前直管段、后直管段、前导流件和后导流件几何形状比较规则，采用结构化网格。为了减少网格数量但不影响网格质量，在前后直管段利用增长函数生成体网格，最大aspect-ratio为2。直管段与导流件之间、导流件与叶轮之间及叶轮所在区域结构比较复杂，采用非结构化网格。网格总数为141.7万。

3.2 仿真过程相关参数设定

由于传感器叶轮叶片与导流件叶片间有较强的相互作用，因而采用非稳态仿真方法。

传感器的计算域被分为3部分，即前直管段及前导流件区域、叶轮所在区域、后导流件及后直管段。叶轮所在区域的motion type设定为Moving Mesh(滑移网格)，其余2个区域设定为静止区域，旋转区域和静止区域通过2对interface面连接在一起。选用k-w SST湍流模型。依据实验测试结果设定入口初始条件。

依据叶轮转速和仿真步数计算时间步长。当各项残差均小于10-5时，认为求解方程收敛。保存收敛后的cas和data文件。

3.3 从三维流场获取TM值的方法

由牛顿运动定律可得传感器叶轮的运动方程：

(1)

式中：T为叶轮所受合力矩；J为叶轮的转动惯量；ω为叶轮旋转角速度；Td为流体通过叶轮对叶片产生的驱动力矩；Tr为流体经过叶片表面时产生的黏性摩擦阻力矩；Th为轮毂表面黏性摩擦阻力矩；Tm为磁电信号检出器阻力矩；Tw为轮毂端面与表面流体的黏性摩擦阻力矩；Tb为叶轮轴与轴承之间的黏性摩擦阻力矩；Tt为叶片顶端与涡轮壳体内壁之间流体流动的黏性摩擦阻力矩。

从CFD仿真三维流场中，可以获取合力矩T，驱动力矩Td，阻力矩Tr、Th、Tw、Tt之和，代入式(1)，可得Tb、Tm之和。由于在流场中无法单独获取这两项的值，在下文中将二者合在一起计算，并定义为TM。

3.4 系统误差的求取

由于理论模型、求解方法、实验条件等因素的影响，实验结果、CFD仿真结果和理论模型预测结果之间总存在一定程度的偏差，称为系统误差。把从流场中获取的力矩直接植入理论模型时，系统误差使得数学模型对传感器性能的预测仍未得到满意的结果。

研究过程中，认为对于同一结构的涡轮流量传感器，在相同的流量点和相同的叶轮转速时，驱动力矩、阻力矩和合力矩三者在仿真流场中获取与数学模型计算之间存在的系统误差是相同的。各流量点对应的系统误差如表1所示。

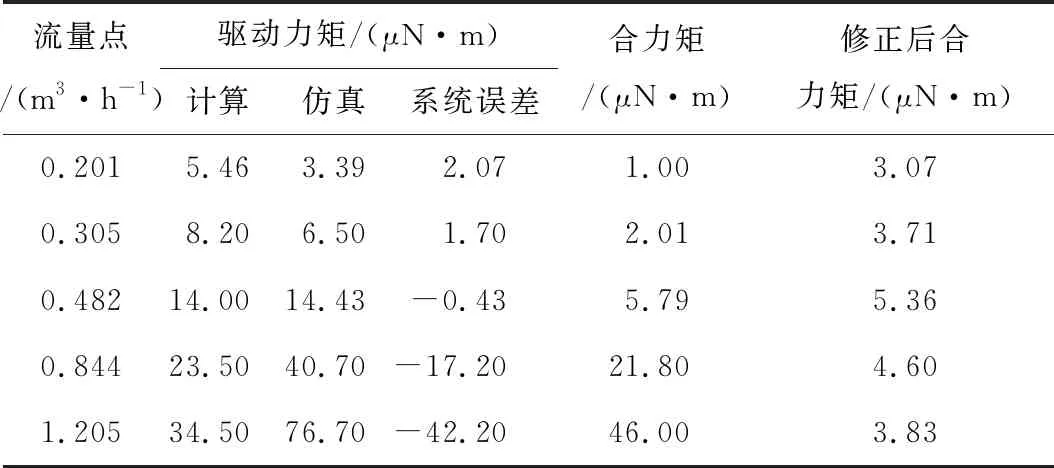
表1 力矩计算结果

研究过程中，需要求取的磁阻力矩是叶轮旋转一周所受磁阻力矩的平均值，因而Tm与叶片的位置无关，而与叶轮的转速有关。根据实验和仿真数据可以拟合出TM的数学表达式：

TM=9.0×10-7+1.35×10-8ω-1.03×10-11ω2

(2)

将式(2)加入文献[9]中数学模型，即完成对现有数学模型的完善，建立适用于小口径涡轮流量传感器的数学模型。

4 完善后数学模型的实验验证

为验证上述方法的有效性和数学模型的准确度，选择4种不同叶轮结构的涡轮流量传感器做实流实验。实验装置和实验方法与上文相同。叶轮结构示意图如图4所示。切角参数η=b/a，其中a为叶片根部的轴向长度，b为叶片顶部的轴向长度。4种传感器的结构参数η分别为1、0.75、0.5、0.25。

利用数学模型预测的结果和实验结果对比如图5所示。由图5可见，修正后的数学模型预测曲线和实验特性曲线趋势相近，并且数值相差不大(平均仪表系数最大误差为1.2%，线性度误差相差0.12%)。因此，所建数学模型的预测结果与实验结果较接近；在结构变化不大时，完善后的数学模型对小口径涡轮流量传感器的性能预测结果与实际测试结果更接近。