基于MSC的低量程SAW压力传感器研究
2021-06-03李媛媛季雪咪
杨 刚,李媛媛,曹 乐,江 蓓,季雪咪
(上海工程技术大学电子电气工程学院,上海 201620)
0 引言
压力检测一直是工程应用和力学方面的热点研究课题。近年来,在狭缝间压力检测[1]、微压力监测[2]、纱线张力性能分析[3]等领域研究开始成为压力检测的重点。压力检测常用传感器类型主要分为压阻式、电容式、电感式和光学式[4-5]。但这类传感器在特殊检测领域存在无法精确检测微小压力的变化和控制复杂环境产生的介入误差的问题[6]。目前,根据声表面波技术所制的传感器凭借精度高、灵敏度高、抗干扰能力强等优势能实现其在低量程压力范围内的检测[7]。
声表面波(SAW)传感器的测量精确度是实现检测的重要条件之一。通过研究发现SAW压力传感器有2个方面因素会影响其在低量程领域的检测精确度。一方面,SAW传感器的叉指换能器(IDT)存在电极内反射问题,易引起频率响应曲线旁瓣干扰,过于严重会使频率响应产生畸变;另一方面,IDT在压电转换中产生部分体声波(BAW),干扰传感器测量精确度[8]。针对传感器存在的这2个关键问题,现研究从传感器结构、IDT位置及IDT结构等方面对传感器改进。例如,文献[9]通过设计谐振梁式的微压力传感器,发现传感器的基片结构会影响其测量灵敏度。文献[10]利用有限元分析方法构建传感器模型,从特征频率、频域、时域等特性分析IDT对频率响应的影响。文献[11-12]的研究利用多条耦合器和双声路对称结构,将沿晶体表面传播的体声波进行分离和消除,抑制三次渡越信号,降低了接收损耗。文献[13]在表面声波纱线张力传感器的研究中采用不同等宽的叉指设计,通过调节叉指宽度改变IDT电极内反射和旁瓣干扰问题。基于此,本文设计一种基于MSC的SAW低量程压力传感器。通过对IDT进行余弦平方函数加权设计,同时加入多条耦合器(MSC)结构,从而达到减少测压过程中因IDT电极内反射导致的频响曲线旁瓣干扰以及抑制和过滤BAW的效果。
1 传感器设计方案和工作原理
1.1 MSC设计方案
MSC的出现为SAW传感器的设计带来了更多的灵活性,并有助于提高器件的部分性能。MSC能够改变SAW在压电基片上传播的声路,减小BAW等虚假信号对声波信号的干扰[14]。同时由于输入与输出均采用余弦平方函数加权的叉指换能器设计,MSC在输入IDT和输出IDT之间调节波传播的耦合度,使输出的频率响应灵敏度提高,从而降低波在传播过程中的损耗。传感器设计示意图如图1所示。

图1 MSC设计方案示意图
假设问询信号激发的声表面波进入能量幅度记为φi,i表示通道。此时,由于通道2没有声能量输入,所以第一个电极声势能φ2=0。激发的声表面波信号从通道1中进入MSC,波在耦合器中传播分为对称和非对称2种模式。2种模式的相位相差π/2,由于衬底是铌酸锂压电基底材料,入射波会在通道1-4和通道2-3的耦合条上感应出声波电势能,分别用φ14、φ23表示。
在对称模式下,2个通道的声波电势相等,相当于电极开路[15]。
φ14=φ23=Aexp(-jkacnp)
(1)
式中:kac为对称模式下机电耦合系数;n为电极数目;p为耦合器节距;A为振幅。
在非对称模式下,2个通道的声波电势大小相等,但是方向相反,相当于电极短路。
φ14=-φ23=Aexp(-jkscnp)
(2)
式中ksc为非对称模式下机电耦合系数。
2种模式相加后,在通道1-4中的声势能为
(3)
在通道2-3中的声势能为
(4)

pNc(ω)=π/(ksc-kac)
(5)
由式(3)和式(4)可以得,当n=0,表面波能量完全在通道1、4中;当n=Nc,能量完全在通道2、3中。因此Nc是表面波能量从一个通道中转移到另一个通道所需的电极条数。它和材料的机电耦合系数成反比。由于ksc和kac都接近于k0,因此ksc+kac≈2k0。当耦合器的指条数等于Nc时,通道1-4的能量将完全耦合到通道2-3中。这就是基于MSC的SAW压力传感器设计的主要依据。
1.2 SAW传感器工作原理
SAW器件的重要工作原理是基于压电效应实现力-电转化,其具有灵敏度高、重复性好、可靠性高以及抗干扰能力强等优势[16]。在文中,SAW压力传感器应用于量程在0~0.2 N范围内的检测,其结构采用双端口延迟线型设计,如图2所示。该传感器由压电基底、金属底座、IDT、MSC、导线、引脚和垫片组成。传感器工作时,外界问询的电信号经输入引脚传播到IDT后,电信号经过压电效应转化为声波信号沿压电基底表面传播[17]。声波信号沿基底表面经过MSC传播到输出IDT,通过逆压电效应转换成电信号输出。

图2 SAW传感器结构示意图
当SAW压力传感器承载压力后,其结构发生形变后,SAW波长也随之发生变化。传播速度以及波长变化共同作用,让频率f发生改变。所以通过测量频率值可以推测接触压力的值。
由SAW理论[18]可以得到
(6)
式中:f为输出频率;vs为SAW传播速度;λ为波长。
由于所设计的SAW传感器的金属极化率为0.5,所以IDT的指长宽度l和指条间隙s相等,即l=s=b0(b0表示没有压力作用下的结果)。假设压力作用下引起小应变δ,则存在:
λ(δ)=2b(δ)=2b0+2δb0=2b(1+δ)=λ0(1+δ)
(7)
v(δ)=v0(1+Kδ)
(8)
式中:λ(δ)为压力作用的波长;λ0为没有压力作用的波速;v(δ)为压力作用的波速;v0为没有压力作用的波速;K为常量。
将式(7)和(8)代入式(6)中,可以得到:
(9)
由于应变δ非常小,可以得到:
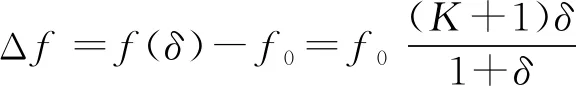
(10)
式(10)中,由于压力作用与应变δ存在对应关系,所以:
Δf≈f0F(K-1)
(11)
通过式(11),本文得到了输出频率的差量和压力呈现线性函数关系,根据此原理,可以根据输出频率的变化量推导出其所受的压力大小。
2 低量程SAW压力传感器设计
2.1 基片材料选择
在检测压力量程为0~0.2 N的范围内,传感器的测量精度会严重影响传感器最终的测量结果。为了探究压电基底材料对于SAW传播的影响,分析了几种可行的压电材料参数,如表1所示。
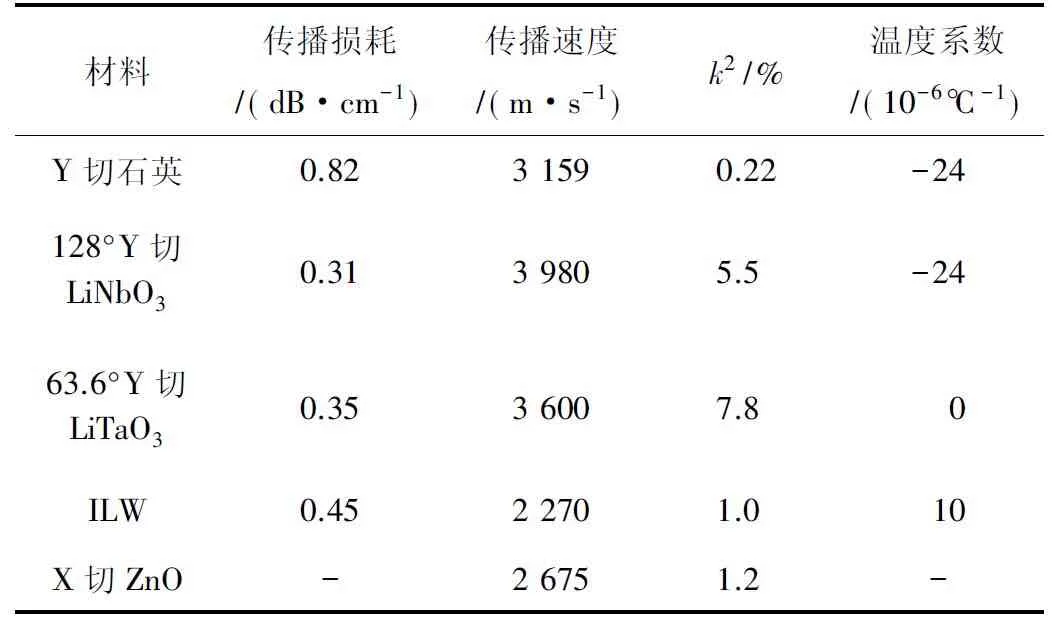
表1 压电基底材料参数
由于该传感器引入MSC设计,其电极数目和压电基底材料的机电耦合系数有很大关系,综合考虑中心频率、延迟、实际结构、功能、性能等综合因素。由表1可以看出128°Y切LiNbO3具有机电耦合系数较好、压电系数大、传播速度快、声衰较小等优势,所以本文采用128°Y切LiNbO3作为压电基底材料。
2.2 IDT位置确定
基片在受力下各点的应力应变存在差异,为了得到最大灵敏度的SAW压力传感器,需要将IDT安放到基片上应力应变最稳定区域,器件结构尺寸如图3所示。

图3 SAW传感器尺寸示意图
利用COMSOL仿真软件对基片进行有限元仿真,在基片的中心施加0.2 N的压力,得到基片的有限元仿真图,如图4所示,其中较深的区域为应力稳定区。从基片的颜色分布可以得到基片上每个位置von Mises应力的变化趋势,如图5所示。图中A、B点应力较小,属于基片上的应力稳定区域,因此将输入和输出IDT分别放置A、B所在位置。通过对基片的材料和尺寸设计仿真得到SAW传感器的基片设计参数,如表2所示。

图4 基片有限元仿真图

图5 基片应力分布示意图

表2 基片设计参数 mm
2.3 低量程SAW传感器设计参数
为抑制SAW传感器的频率响应曲线旁瓣干扰,需对输入输出IDT的结构进行改进。将输入输出IDT均采用余弦平方函数加权包络,并采用假指进行包络填充,设计版图如图6所示。加权的余弦平方函数w(t)为
w(t)=0.08+(1-0.08)cos2(2πtτ)=0.54+0.46cos(πtτ),|t|≤τ
(12)
式中τ为输入IDT的时长。

图6 余弦平方函数加权IDT设计版图
由于在延迟路径上采用了耦合器,耦合器能够改变SAW传输通道和相位反转。因此利用耦合器能改变波传输通道的优势过滤体声波扰动。同时耦合器相位反转实现余弦平方函数加权输入输出IDT间能量转换。
根据多条耦合器的阻带频率确定f0:
(13)
式中;v为声表面波的传播速度;p为多条耦合器的周期。
一般要求耦合器的工作频率f在阻带频率的1/2处,即
f=0.5f0
(14)
由于f=v/λ,所以耦合器的周期,也就是节距p=λ/4=20 μm。耦合器电极宽度a=λ/8=10 μm。
根据耦合器设计原理,当耦合器2个通道的孔径相同时,能量完全转移所需要的金属条数为
(15)

(16)
将s=1/4,θ=π/2带入式(16):

(17)
由于后一项是对称区间上的奇函数,积分值为零。所以式(17)可以写成

(18)
对于压电基底材料为128°Y切LiNbO3,要使得能量最大效率转移需要多条耦合器最小电极数目为114条。经过前文的分析,设计了基于MSC的SAW压力传感器,其设计参数如表3所示。
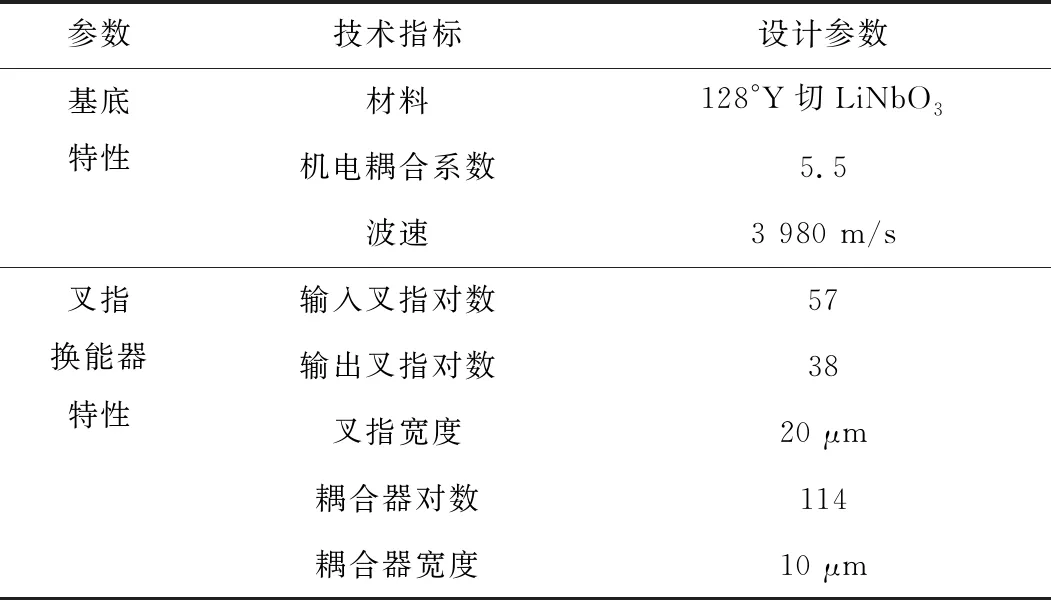
表3 传感器设计参数
3 传感器测试与结果分析
3.1 传感器测试
在前期研究设计的基础上对传感器进行制作和加工,得到基于MSC的低量程SAW压力传感器,如图7所示。

图7 传感器实物图
为检测设计和制备的低量程SAW压力传感器的合理性,需对传感器执行实际环境下的检测环节。传感器由于压力引起基底形变及SAW传播特性改变,最终致使中心频率的偏移。因此采用型号为E5061A的安捷伦网络分析仪测试传感器的频率响应。
因传感器的受压范围在0~0.2 N,选取1~20 g的砝码。在测试设备和环境完善的条件下,以0 g为起点,后一项比前一项多1 g,依次增至20 g,再从20 g起以1 g为差递减至0 g,记录网络分析仪在各项上的频率响应。
由于测试过程中波动较大,待频率响应稳定后得到传感器的频率响应,如图8所示。通过改进余弦平方函数加权IDT和引入MSC的设计。传感器的频率响应曲线在靠近中心频率处的体声波干扰得到有效消除,旁瓣得到合理的抑制。

图8 传感器的频率响应图
每次压力加载后待频率响应波动稳定后多次记录,最终选取均值。其中1组数据结果如表4所示。

表4 频率和压力的测试数据
3.2 传感器结果分析
根据测试数据,通过线性回归分析理论建立输入压力和输出频偏的线性回归最小二乘法模型。定义f0作为SAW的中心频率,f作为输出频偏,则压力和频差间关联用函数表示为
F(Δf)=k0+k1Δf+k2Δf2+k3Δf3+…+knΔfn
(19)
式中:F为传感器承载的压力;Δf为频率偏移量间的差值。
根据最小二乘法模型,通过MATLAB软件对测试结果进行拟合训练,得到拟合曲线如图9所示。最终,SAW压力传感器的输入、输出变量之间的多项式拟合关系为
Δf=0.000 003x6-0.000 166x5+0.002 714x4-0.009 942x3-0.152 688x2+4.683 220x+91.992 021
(20)

图9 SAW传感器频率与压力的关系图
4 结束语
设计了基于MSC的低量程SAW压力传感器。为减少BAW干扰和抑制其输入输出频率曲线的旁瓣,在SAW传播路径上引入多条耦合器,同时于设计中对输入输出IDT进行了余弦平方函数加权设计。经过实验证明,该设计的理论值与实验结果具有较好的一致性,干扰抑制效果明显。
