微纳结构超疏水表面参数影响含不凝气蒸汽冷凝传热的理论分析
2021-06-03贺征宇彭本利苏风民纪玉龙马鸿斌
贺征宇,彭本利,苏风民,纪玉龙,马鸿斌
(大连海事大学船舶与海洋工程学院,辽宁大连116026)
引 言
滴状冷凝具有出色的传热性能,它的传热效率相比于膜状冷凝通常要高出一个数量级[1-2],因此在海水淡化、燃料电池、石油化工、空调系统、电子设备冷却等领域受到了广泛关注。通过制备超疏水表面形成滴状冷凝能够达到强化换热的目的,在烟气冷凝脱硫、空调除湿、微电子元器件冷凝等方面都起到了重要作用。
液滴在超疏水表面形成Cassie湿润状态时,具有接触角大、接触角滞后小的特点,液滴容易从表面脱落,提高液滴脱落频率从而强化换热。超疏水表面结构的改变会影响液滴的尺寸及分布情况,对于冷凝传热的性能有很大的影响[3-6]。对于纯蒸汽的滴状冷凝,Feng等[7]通过实验研究表明致密的表面微纳结构能够形成稳定的Cassie湿润态。Dietz等[8]的研究发现,超疏水表面上液滴尺寸的减小能使传热系数提高2倍左右。同时大量的实验[9-11]也证明了小液滴对于滴状冷凝传热性能的促进作用。然而对于含有不凝性气体的滴状冷凝,Eimann等[12-13]的研究表明,对于混合蒸气的滴状冷凝过程,分布在冷凝表面的大液滴会对流动边界层产生扰动,通过强化显热的传递过程而改善总的传热系数。周兴东等[14]通过实验也发现大液滴的脱落运动会伴随气液界面周期性的振荡与脉动过程,成为强化传热的主要因素。因此不凝气浓度的变化会影响液滴脱落半径对滴状冷凝传热性能的调控作用。
纯蒸汽滴状冷凝传热的研究目前已比较完善,而针对含不凝气蒸汽的滴状冷凝传热模型仍有较大的研究空间。Jiang等[15]参考了化学气液吸收的相关理论,结合目前广泛应用的滴状冷凝模型,建立了基于气液界面热通量平衡的传热模型。Baghel等[16]对纯蒸汽冷凝模型中的相际热阻进行了修正,引入了与不凝气质量分数相关的修正系数,模型计算结果与实验值具有良好的吻合性。
本文将不凝气作为一个独立的热阻,耦合传质模型建立了含不凝气蒸汽的滴状冷凝传热模型。利用竖直壁面上液滴的力平衡,计算得到了超疏水结构表面液滴脱落半径与表面柱间距之间的关系。从单位半径液滴热通量的角度分析了不同过冷度、不同不凝气含量下,超疏水表面结构参数对于滴状冷凝传热性能的影响。
1 液滴脱落半径的确定

Jung等[17]的研究表明,当液滴的凹陷远大于微柱高度时,液滴接触柱间空腔底部从而发生从Cassie态到Wenzel态的转变,如式(1)所示:
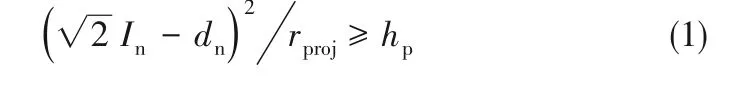
一方面取纳米柱间距In=800 nm,能满足微米级的液滴保持Cassie态。另一方面,对于纳米级的液滴,由于不凝气的存在,液滴核化通常在柱顶发生,而在柱间底部则很少发生[18-19]。因此在本文的计算过程中可以假设液滴始终为Cassie态,改变微米柱间距不会影响液滴的湿润状态。
采用Qi等[20]提出的竖直壁面液滴的力平衡模型,将存在接触角滞后的液滴近似为球冠状,通过壁面对液滴的黏附功与液滴自身的重力矩功相平衡计算液滴的脱落半径,如图1所示。
对于结构表面,液滴与壁面的接触面积为[21]:

通过液滴的黏附功与重力矩功平衡,可以求得液滴的脱落半径为[22]:
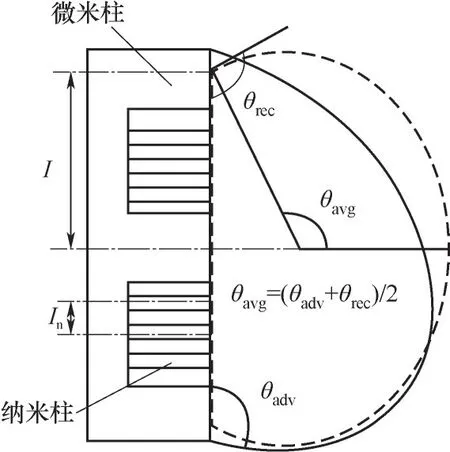
图1 竖直壁面液滴接触角简化图Fig.1 Simplified view of contact angle of a drop on vertical wall
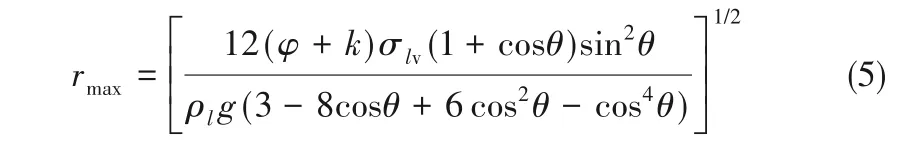
图2为不同过冷度下液滴脱落半径随柱间距的变化关系。为使计算结果更为直观,取I/d为横坐标。从图中可以看出随着柱间距与微柱直径比值的增大,液滴的脱落半径呈减小趋势,且过冷度对脱落半径的影响不大。由式(4)也可以看出表面过冷度仅影响液滴表面张力的大小,表面固液分率值为影响液滴脱落半径的主要因素。
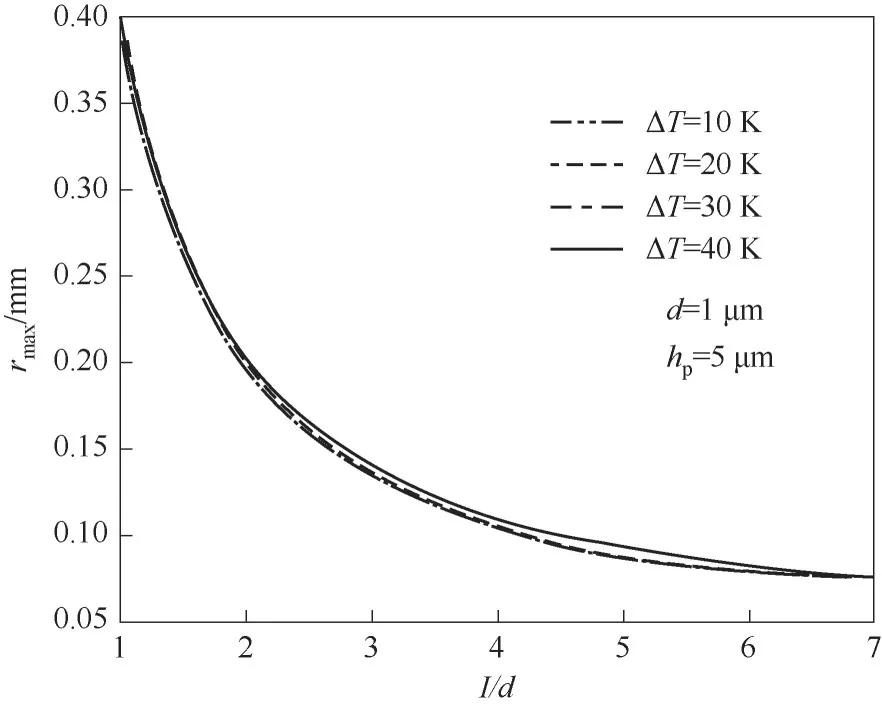
图2 不同过冷度下液滴脱落半径与柱间距的关系Fig.2 Relationship between droplet departure radius and micro-pillar spacing under different surface subcooling degrees
2 含不凝气的滴状冷凝传热模型
2.1 通过单个液滴的传热
对于含不凝气的蒸汽滴状冷凝,取空气作为不凝性气体时,文献的实验结果[23]表明在相同的热通量下,不凝气的存在没有明显改变液滴的分布、脱落半径和表面更新频率。本文假设在液滴的生长过程中,液滴上方的不凝气层处于稳定状态,在纯蒸汽单个液滴导热模型[20,24-26]的基础上串联了一个由不凝气引起的、阻碍传热的热阻Rn,称为当量不凝气热阻。图3为液滴冷凝传热模型及对应热阻的示意图。
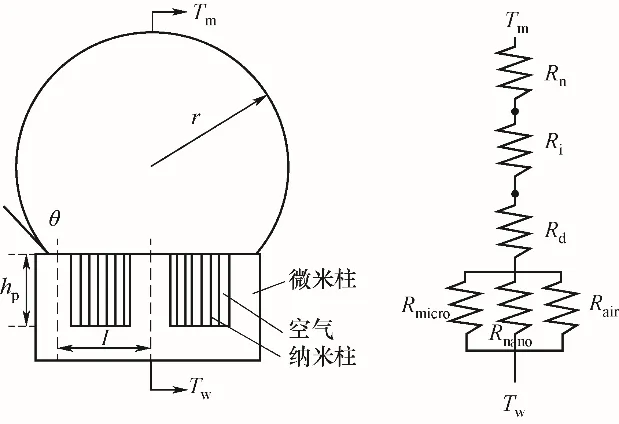
图3 液滴冷凝模型与热阻示意图Fig.3 Schematic view of dropwise condensation model and thermal resistance
不考虑促进层与基底的热阻,单个液滴传热过程的总热阻Rtotal可以表示为:
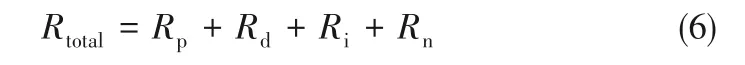
式中,Rp为超疏水表面结构的导热热阻;Rd为液滴导热热阻;Ri为相际传热热阻,分别计算如下[24,27-28]:
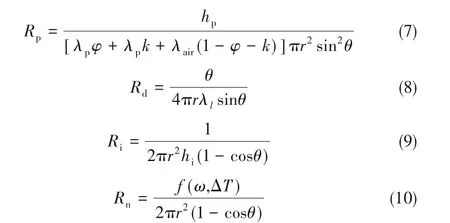
式中,λl、λair分别为冷凝液、空气的热导率。hi为气液界面传热系数[27]:
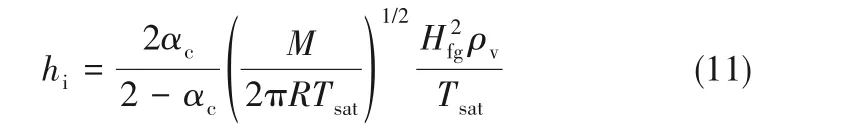
式中,αc为冷凝系数[12,29],本模型由于引入了不凝气热阻,液滴气液界面可看作纯蒸汽的冷凝过程,αc=1。f(ω,ΔT)是一个与不凝气体积分数ω和冷凝表面过冷度ΔT相关的函数,其中ω=(Pm-Psat)/Pm。通过传热模型和Zheng等[30-31]提出的传质模型相耦合,基于Ma等[9]的不凝气浓度为0~5%,过冷度为5~20 K条件下的实验数据,拟合分析得到了相应的实验关联式,可以用来定量地分析不凝气浓度对冷凝换热的影响。当环境压力Pm=0.1 MPa时,f(ω,ΔT)的表达式为:f(ω,ΔT)=ω1.9874ΔT-0.1177(-5.4403ΔT+754.4304)×10-5(12)
通过单个液滴的传热速率为:
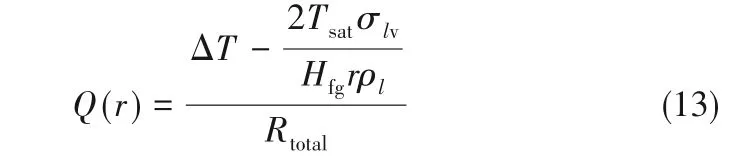
2.2 液滴分布函数
冷凝表面存在两种生长方式的液滴,分别为直接冷凝生长和合并生长的液滴。根据众数平衡原理,直接冷凝生长的液滴分布函数n(r)为[24,32]:

式中,Hfg为汽化潜热。A1、A2、A3是与冷凝液物性、表面过冷度、本征接触角及促进层物性相关的参数,B1、B2是与液滴脱落半径、最小半径及吹扫时间τ相关的参数,分别为[23-24,36]:
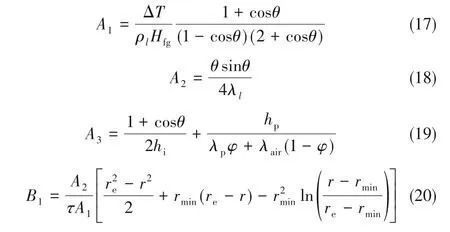
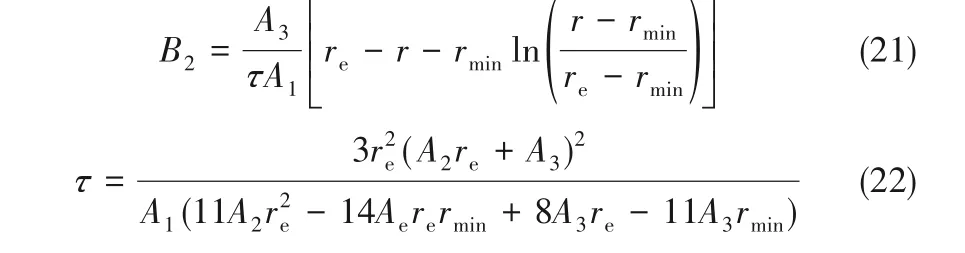
对于主要依靠合并长大的液滴,分布函数采用Rose[1]提出的半经验公式:
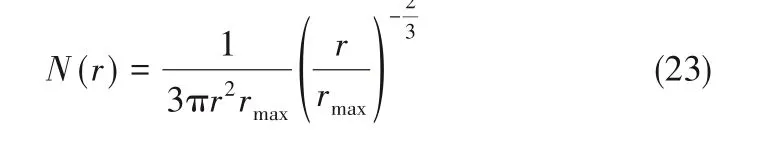
2.3 冷凝表面平均热通量
结合上述单个液滴的传热公式和液滴的尺寸分布公式,可以得到滴状冷凝表面的平均热通量表达式:
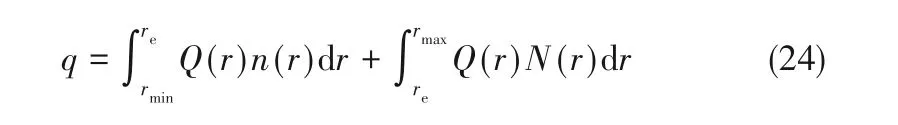
2.4 传热模型可靠性验证
为验证上述传热模型的可靠性,将本模型计算得出的预测值与文献[30,37]的实验结果进行了比较。表1给出了理论计算的相关参数,图4(a)、(b)分别为不凝气含量为14%和97.4%时计算结果与实验数据的误差。结果表明计算值与实验值的误差在相应过冷度下都小于20%,证明了传热模型具有可靠性,能够对高不凝气含量下的冷凝过程进行预测和分析。
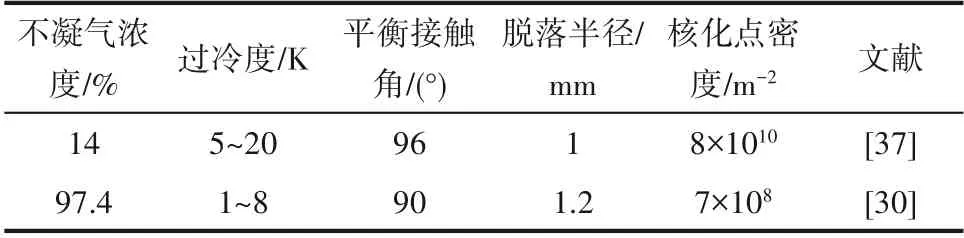
表1 理论计算的参数Table 1 Parameters of the theoretical calculation

图4 传热模型的预测结果Fig.4 Prediction resultsof heat transfer model
3 超疏水表面结构参数对冷凝换热的影响
本文的计算条件为:混合蒸气压力Pm=0.1 MPa,微柱材料为CuO,微柱直径d=1μm,柱高hp=5μm,热导率λp=70 W/(m·K)。核化点密度Ns=2.5×1011/m2。过冷度ΔT=5~20 K。分析了不同不凝气浓度下柱间距对超疏水结构表面换热性能的影响。
3.1 不凝气浓度低于20%时柱间距对传热性能的影响
图5为不凝气浓度低于20%时q/qmax与表面柱间距的关系。其中q为冷凝表面的平均热通量,qmax为在柱间距取值范围内计算得到的最大热通量值。计算条件取过冷度ΔT=5 K,不凝气浓度ω分别为5%、10%、15%和20%。当不凝气浓度一定时,随着I/d值的增大,超疏水表面固液分率值相应减小,表面平均热通量先增大后减小,存在一个使传热量最大的I/d值。随着不凝气浓度的增加,表面热通量的最大值和变化幅度均减小,且I/d的最佳值呈增大趋势。这是由于在低不凝气浓度下,表面微结构的导热热阻是传热的主要热阻,随着I/d值的增大,一方面微结构内部气相部分体积增大,导致微结构总体热阻增大,对传热起抑制作用;另一方面由于液滴分布密度增大,单位半径液滴热通量增大,对传热有促进作用。在两者的共同作用下存在一个I/d的最佳值。
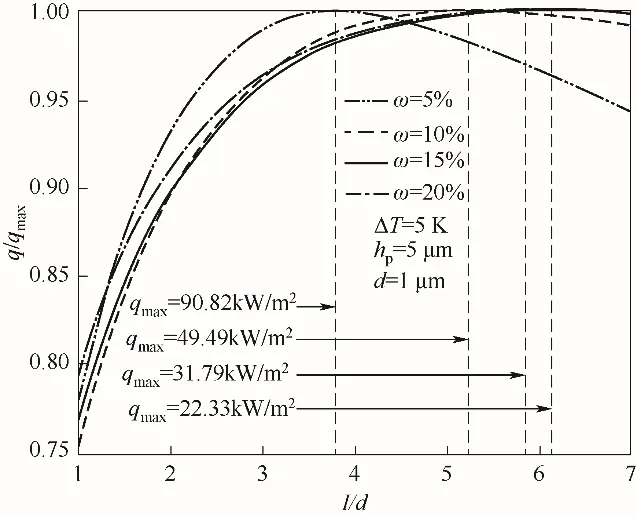
图5 不凝气浓度低于20%时q/q max与表面柱间距的关系Fig.5 Relationship between micro-pillars spacing and q/q max when the concentration of non-condensable gas is less than 20%
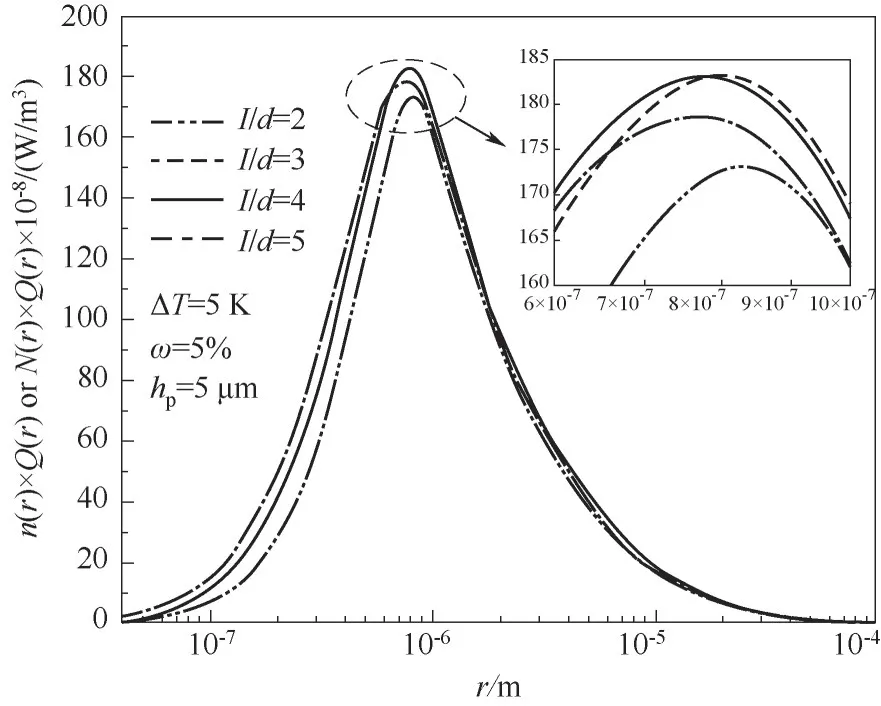
图6 不凝气浓度5%时不同柱间距下单位半径液滴的热通量Fig.6 Heat flux per unit droplet radius with different micro-pillars spacing when the concentration of non-condensable gas is 5%
选取不凝气浓度ω=5%的情况,对单位半径液滴热通量进行分析,如图6所示。I/d取2~5,图中内插小图为图中椭圆部分的放大图。可以看到I/d的值从2增长到3时,由于表面固液分率减小导致液滴分布密度增大,总的热通量也相应增大;当I/d的值从4增长到5时,此时表面微结构热阻的增大更为显著,对传热的抑制作用更强,故总的热通量呈减小趋势。I/d在取值范围内存在一个最佳值。
3.2 不凝气浓度高于20%时柱间距对传热性能的影响
图7给出了不凝气浓度ω分别取20%、40%、60%和80%时q/qmax与I/d的关系。当不凝气浓度高于20%时,可以看到随着不凝气含量的升高,表面热通量的变化率降低,I/d的最佳值呈减小趋势,这与不凝气浓度低于20%时的变化规律相反。这是由于不凝气开始成为主要热阻,此时液滴脱落半径的大小对冷凝传热性能的影响更为显著。
图8为不凝气浓度ω=60%时,单位半径液滴的热通量,I/d取3~6。图中内插小图为图中椭圆部分的放大。可以看出随着I/d值的增大,液滴的分布密度增大,表面热通量也相应增大。同时由于表面固液分率减小,竖直壁面对液滴的黏附功相应减小,液滴的脱落半径rmax相应减小(如图8中小图所示),表面热通量也因此降低。由于在高不凝气浓度下,传热温差主要集中在不凝气侧,因此单位半径热通量(纵坐标)的增大对于传热的促进作用要小于脱落半径(横坐标)的减小对于传热的抑制作用,故随着脱落半径的减小,传热性能呈下降趋势。并且随着不凝气浓度的提高,液滴脱落半径的减小对传热的抑制作用会更为明显。
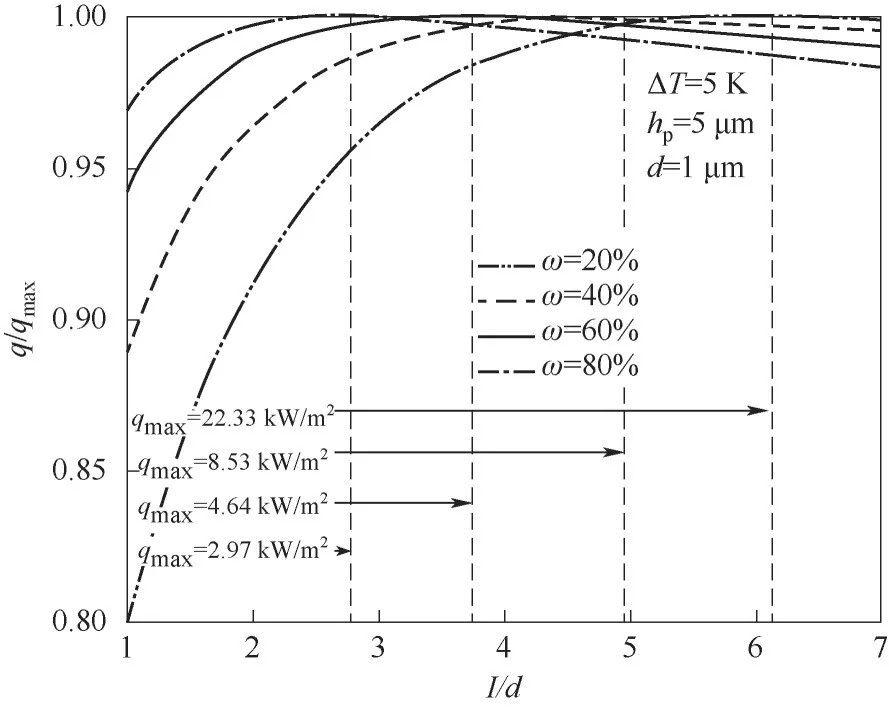
图7 不凝气浓度高于20%时q/q max与表面柱间距的关系Fig.7 Relationship between micro-pillars spacing and q/q max when the concentration of non-condensable gas is more than 20%
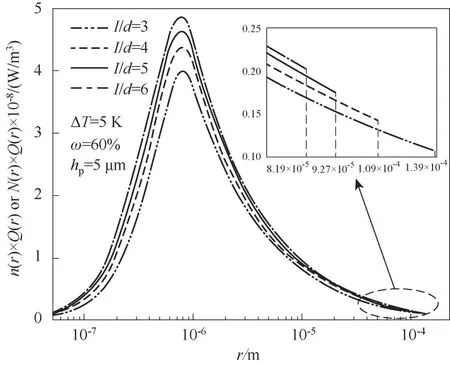
图8 不凝气浓度60%时不同表面柱间距下单位半径液滴的热通量Fig.8 Heat flux per unit droplet radius with different micro-pillars spacing when the concentration of non-condensable gas is 60%
3.3 表面柱间距的最佳值
图9给出了不同过冷度下冷凝表面最佳柱间距随不凝气浓度的变化关系,可以看到当过冷度为5 K时,I/d的最佳值在不凝气浓度低于20%时呈增长趋势,最大值为6.15。通过上述分析可以得知,在低不凝气浓度下,单位半径液滴热通量较大,此时液滴分布密度与表面微结构的导热热阻为影响传热性能的两个主要因素。随着不凝气浓度升高,不凝气热阻增大,表面结构热阻的影响力下降,故最佳柱间距值也相应增大。
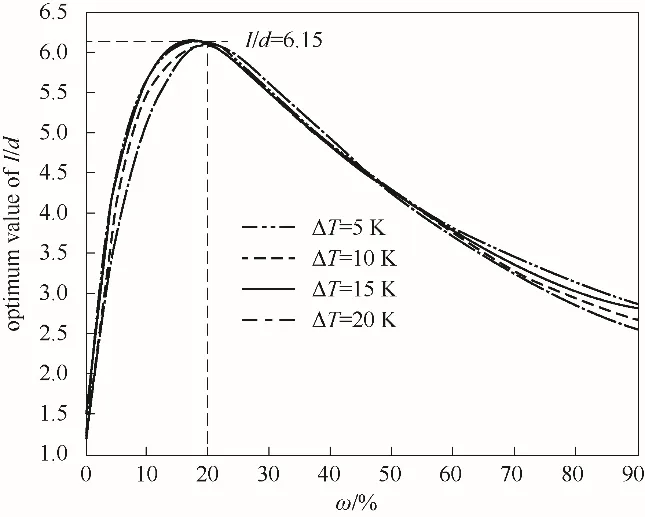
图9 不同过冷度下最佳柱间距随不凝气浓度的变化关系Fig.9 Relationship between optimum value of micro-pillars spacing and concentration of non-condensable gas under different subcooling degrees
当不凝气浓度高于20%后,I/d的最佳值呈减小趋势,这是由于随着不凝气浓度的提高,不凝气开始成为主要热阻,单位半径液滴热通量减小,液滴脱落半径减小对传热的抑制作用开始被放大,此时液滴分布密度和脱落半径成为影响传热性能的主要因素。柱间距的减小使液滴脱落半径增大,故随着不凝气浓度升高,最佳柱间距值相应减小。
从图9还能看出,随着过冷度的增加,最佳柱间距的最大值和所对应的不凝气浓度几乎没有改变,但在高不凝气含量下(ω>60%),高过冷度所对应的最佳柱间距更大。这是由于过冷度的增大会强化换热,同时不凝气热阻也会随过冷度的增大而增大。在高不凝气含量下前者的促进作用更为明显,故最佳柱间距曲线的斜率随过冷度的提高而减小。
4结 论
本文基于竖直壁面上液滴黏附功与重力矩功的平衡,确定超疏水表面不同微纳结构下液滴的脱落半径。通过建立含不凝气的蒸汽滴状冷凝传热模型,在核化点密度Ns=2.5×1011/m2,混合蒸气压力为0.1 MPa的条件下,研究了不同不凝气浓度和过冷度下,超疏水表面结构特性对于滴状冷凝传热性能的影响,得到了以下结论。
(1)超疏水表面微米级圆柱半径一定时,通过改变柱中心距控制表面固液分率,液滴脱落半径随柱间距的增大而减小。
(2)通过对超疏水结构表面热通量的计算,在不同不凝气含量下超疏水表面柱间距对传热性能的影响不同。在低不凝气含量下,增大柱间距来减小表面结构热阻有利于传热性能的提高;而在高不凝气含量下,减小柱间距使液滴脱落半径增大更能强化换热。
(3)超疏水表面微柱直径保持不变时,柱间距存在最佳值,且最佳值随着不凝气浓度的提高呈先增大后减小的趋势。过冷度的增大对最佳柱间距的最大值影响不大。
符号说明
Asl——固液接触面积,m2
d——表面微米柱直径,μm
dn——表面纳米柱直径,nm
Hfg——汽化潜热,J/kg
hi——气液界面传热系数,W/(m2·K)
hp——表面微柱的高度,μm
I——超疏水表面微米柱的中心距,μm
In——超疏水表面纳米柱的中心距,nm
k——纳米柱的固体分数,%
M——水的分子量
Mg——重力矩,N·m
N(r)——合并液滴的密度,m-2
Ns——核化点密度,m-2
n(r)——独立长大液滴的密度,m-2
Q——单个液滴的传热速率,W
q——冷凝表面平均热通量,W/m2
R——传热热阻,K/W
r——液滴半径,m
re——液滴临界半径,m
rmax,rmin——分别为液滴脱落半径、最小半径,m
rproj——液滴投影半径,r
ΔT——过冷度,K
αc——冷凝系数
θ——液滴的表观接触角,(°)
θadv,θrec——分别为液滴的前进角、后退角,(°)
θavg——液滴接触角的计算平均值,(°)
λ——热导率,W/(m·K)
ρ——密度,kg/m3
σ——表面张力,N/m
τ——吹扫时间,s
φ——微米柱的固体分数,%
ω——不凝气含量,%
下角标
air——空气
d——冷凝液滴
i——气液接触界面
l——冷凝液
m——空气-水的混合气
n——不凝气
p——微柱
sat——饱和水蒸气
v——水蒸气
w——冷凝壁面
