有界Heyting 代数的扩张模糊LI-理想
2021-06-03刘春辉
刘春辉
(赤峰学院 数学与计算机科学学院,内蒙古赤峰 024000)
0 引言
非经典数理逻辑是一门涉及数学与计算机科学的交叉学科,对与不同形式的非经典数理逻辑推理系统相对应的非经典数理逻辑代数系统的研究是该理论体系的重要研究方向之一[1]。以荷兰数学家的名字命名的Heyting 代数是一类在直觉模糊逻辑中起关键作用的非经典数理逻辑代数系统,逻辑的排中律在Heyting 代数中通常不必成立。从逻辑层面看,Heyting 代数是对经典二值逻辑命题演算推理系统的基础性推广,经典二值逻辑的命题演算推理系统是Heyting 代数的一个重要且简单的例子。从代数层面看,Heyting 代数是对Boole 代数做一般化处理后得到的一个偏序集,完备Heyting 代数(也称Frame)是无点化拓扑研究领域的一个中心概念[2]。同时,Heyting 代数又与FI 代数、MV 代数、BL 代数和格蕴涵代数等有密切联系。迄今为止,对Heyting代数系统性质和结构的研究已非常深入,研究成果在众多领域得到了十分成功的应用[3-10]。
偏序结构被布尔巴基学派冠名为三大数学母结构之一,滤子和理想概念最早作为偏序集的两类相互对偶的特殊子集被提出。在非经典数理逻辑理论研究中,作为研究非经典数理逻辑代数及与其相对应的逻辑推理系统完备性的2 个重要工具,滤子和理想不断被扩充和推广。文献[11]指出,Heyting 代数的滤子不但可用格论(一类特殊的偏序集)语言加以定义,而且也可用逻辑语言定义。更值得关注的是,2 种形式的定义是相互等价的,表明滤子概念在揭示Heyting 代数系统结构特征过程中发挥了不可替代的重要作用。研究表明,在否定运算满足对合(正则)性质的非经典逻辑代数系统中,各种理想的性质均可借助与之相对偶的滤子的性质获得。所以,对理想理论的研究只有在否定运算不满足对合性质的代数系统框架下才有意义。Heyting 代数恰好是这类代数系统的典型代表之一,然而,Heyting代数一般无最小元0,即无界,忽略了对在Heyting代数中引入理想概念的思考。为弥补这一研究空白,借助于理想概念揭示Heyting 代数及直觉主义命题逻辑推理系统的新途径和新方法,文献[12-13]运用Zadeh 模糊集[14]理论在有界Heyting 代数中引入了模糊LI-理想,并考查了其性质。本文在有界Heyting 代数中引入扩张模糊LI-理想,并讨论其性质、刻画和应用,获得了若干具有理论意义的有趣结果,是对文献[12-13]工作的进一步深化。
1 预备知识
为行文简洁,本节介绍一些关于有界Heyting代数及其模糊LI-理想的基本概念和基本结论。




2 扩张模糊LI-理想


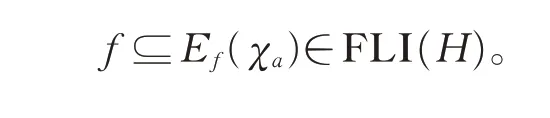

表1 二元运算“→”的定义Table 1 Definition of unary operator“→”





定义7设(H,≤,→,0,1) 为有界Heyting 代数,f∈FLI(H)且κ∈FS(H)。若Ef(κ)=f,则称f是H的关于H上的模糊子集κ的不变模糊LI-理想。
例3设格H={0,a,b,c,1},且H的Hasse 图如图1 所示,H上的二元运算“→”的定义如表2 所示,则(H,≤,→,0,1) 为有界Heyting 代数。定义f∈FS(H),使得f(0)=f(a)=β,f(b)=f(c)=f(1)=α,0 ≤α<β≤1,则可验证f∈FLI(H)为H的关于H上的模糊子集χ1的不变模糊LI-理想。事实上,因为对∀x∈H,有Ef(χ1)(x)=f(x∧1)=f(x),故Ef(χ1)=f。
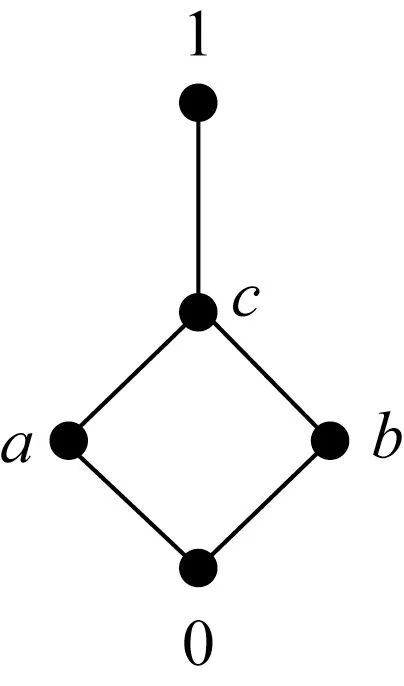
图1 格H 的Hasse 图Fig.1 The Hasse diagram of lattice H

表2 H 上的二元运算“→”的定义Table 2 Definition of unary operator“→”on H
定理6设(H,≤,→,0,1) 为有界Heyting 代数,f∈FLI(H)且κ,ω∈FS(H)。
(1)若κ(1)=1,则f是H的关于κ的不变模糊LI-理想;
(2)如果κ⊆ω且f是H的关于κ的不变模糊LI-理想,则f也是H的关于ω的不变模糊LI-理想。

3 应用扩张模糊LI-理想构造格结构



4 结论与展望
有界Heyting 代数是一类典型的否定运算不满足对合(正则)性质的非经典数理逻辑代数,本文基于此代数框架对模糊LI-理想的相关话题进行了探索和研究。引入了有界Heyting 代数(H,≤,→,0,1)的模糊LI-理想f关于H上的模糊子集κ的扩张模糊LI-理想和不变模糊LI-理想的概念,给出了扩张模糊LI-理想和不变模糊LI-理想的若干重要性质及等价刻画;讨论了扩张模糊LI-理想与生成模糊LI-理想之间的关系;考查了扩张模糊LI-理想在构造格结构过程中的应用,证明了有界Heyting 代数(H,≤,→,0,1)的模糊LI-理想全体之集FLI(H)的三类特殊子集在模糊包含序⊆下均构成cHa。这些结论的获得,为进一步深入理解和把握(有界)Heyting 代数及与之对应的直觉主义命题逻辑推理系统的性质和结构特征提供了极大帮助;也为系统研究否定运算不满足对合(正则)性质的非经典数理逻辑代数系统及其(模糊)理想问题提供了新的方法和途径。
