考虑服务技能约束的家政服务双边稳定匹配方法

孔德财，刘长平，崔杰

（1.淮阴工学院管理工程学院，江苏淮安 223003；2.江苏省智能工厂工程研究中心，江苏淮安 223003）

0 引言

随着经济社会的发展以及城市生活和工作节奏的加快，居民对家政服务呈多样性需求；与此同时，农村人口不断涌入城市，大学毕业生逐年增加，在加剧就业压力的同时也在一定程度上扩大了家政服务人员的规模，由此促进了我国家政服务行业的迅猛发展［1-2］。然而，长期制约家政服务行业蓬勃发展的重要问题之一是，即便雇主给出高工资有时也难以雇到合适的家政服务人员，而家政服务人员也经常因难以找到满意工作而苦恼，具体体现在雇主的高解雇率和家政服务人员的高辞职率［3］。雇主和家政服务人员间无法实现相对稳定的匹配状态，是造成当前家政服务市场混乱无序的重要原因之一。因此，考虑雇主和家政服务人员的双方需求，获得双方稳定匹配，降低搜寻成本，提高匹配满意度，对于维护家政服务市场秩序，促进家政服务行业的健康发展具有重要的现实意义。

GALE 等［4］在研究男女婚恋匹配和大学录取问题时，首次提出稳定匹配概念，并给出了获得稳定匹配的延迟接受算法。ROTH［5］采用实证研究方法，对比了英国国民健康服务（NHS）在不同地区的实习生招聘制度，证实了稳定匹配机制的重要性。SHAPLEY 和ROTH 因在稳定匹配理论及机制设计实践方面的贡献，被授予2012 年诺贝尔经济学奖。关于稳定匹配理论的研究和应用目前已从男女婚恋匹配、大学录取、医院和实习生匹配［6-9］等传统匹配市场扩展至其他服务行业。BARRON 等［10］针对国际货币基金组织中的人员与部门匹配机制缺陷，提出了采用基于延迟接受算法的集中化稳定匹配机制。KORKMAZ 等［11］为解决军队中人员类型与岗位匹配问题，构建了基于层次分析法和稳定匹配算法的决策支持系统。GHAROTE 等［12］采用集中化稳定匹配机制研究了实习生与软件项目需求间的匹配问题，针对软件项目需求具有任意长度无差异偏好列表的特点，建立了再培训和重新安置成本最小化的优化模型，并设计了基于GRASP 的散射搜索算法求解大规模问题。PENG 等［13］针对干散货航运市场中船舶与货物之间的匹配问题，构建了以船货总体效用最大为目标的优化稳定匹配模型，开发了基于Gale-Shapley 算法的价格博弈机制，研究由托运人主导的市场、由承运人主导的市场和均衡市场3 种情景，结果表明，如果弱势参与者以价格博弈机制出价，即使他们处于劣势也可能获得更多收益。袁铎宁等［14］针对手术医生和择期手术患者的一对多双边匹配问题，构建了满足期望水平的医患稳定匹配方案的多目标优化模型。李铭洋等［15］针对具有属性期望的多属性双边匹配问题，依据行为决策理论中的失望理论，构建了以双方主体感知效用最大化为目标的多目标稳定匹配模型。

虽然关于稳定匹配理论的研究取得了一些成果，有些甚至已被应用于现实生活［16-19］，但目前尚未见关于家政服务人员和雇主的稳定匹配研究。因此，关于家政服务人员和雇主的稳定匹配研究具有一定的理论意义和实际应用价值。基于此，笔者在已有稳定匹配理论基础上，提出一种考虑服务技能约束的家政服务双边稳定匹配方法。

1 问题描述

用HSM(a，b，c，d)表示家政服务人员与雇主的双边匹配问题，其中，a表示一名家政服务人员可以匹配的雇主最大数量；b表示雇主需要的家政服务人员最大数量；c表示家政服务人员拥有的家政服务技能数量；d表示雇主需要的家政服务技能数量。本文研究HSM(1，1，n，1)，即一名家政服务人员最多可以为一名雇主服务，一名雇主只雇佣一名家政服务人员，家政服务人员拥有多项服务技能而每名雇主只需要一项服务技能。

设W={W1，W2，…，Wm}为m名家政服务人员组成的集合，其中Wi代表第i名家政服务人员，i=1，2，…，m；E={E1，E2，…，En}为n名雇主组成的集合，其中Ej代表第j名雇主，j=1，2，…，n。在雇主雇佣家政服务人员时，家政服务人员拥有的服务技能只有在满足雇主需要的服务技能时，二者才可能实现最终匹配，因此，需考虑技能匹配约束。设S={S1，S2，…，Sl}为家政服务技能集合，其中Sk代表第k项服务技能，k=1，2，…，l。家政服务人员具备的技能记为矩阵P=[pik]m×l，其中pik=0 或1。pik=0 表示家政服务人员Wi不具备第k项技能；pik=1 表示家政服务人员Wi具备第k项技能，i=1，2，…，m，k=1，2，…，l。雇主需要的服务技能记为矩阵Q=[qjk]n×l，其中qjk=0 或1。qjk=0 表示雇主Ej不需要第k项服务技能，qjk=1 表示雇主Ej需要第k项服务技能，j=1，2，…，n，k=1，2，…，l。

在家政服务人员与雇主的双边匹配问题中，雇主不仅对家政服务人员的服务技能有要求，还会依据家政服务人员的性别、年龄、工作经验等进行总体评价，并对家政服务人员进行偏好排序。同样，家政服务人员在选择雇主时也会考虑工资待遇、工作环境、工作地点等，并进行相应的雇主偏好排序。家政服务人员Wi对雇主Ej的偏好排序记为矩阵R=[rij]m×n，i=1，2，…，m，j=1，2，…，n，其中rij∈{1，2，…，n+1}，若rij∈{1，2，…，n}，则表示家政服务人员Wi将Ej排在第rij位；若rij=n+1，则表示对家政服务人员Wi而言，雇主Ej是不可接受的。雇主Ej给出的家政服务人员Wi的偏好排序记为矩阵T=[tij]m×n，i=1，2，…，m，j=1，2，…，n，其中tij∈{1，2，…，m+1}，若tij∈{1，2，…，m}，则表示雇主Ej将家政服务人员Wi排在第tij位；若tij=m+1，则表示对雇主Ej而言，家政服务人员Wi是不可接受的。若家政服务人员Wi给出的雇主Ej的序值rij越小，则Wi对Ej越满意，反之亦然；类似地，若雇主Ej给出的家政服务人员Wi的序值tij越小，则Ej对Wi越满意，反之亦然。

下面给出偏好可接受对、技能可接受对、可行技能约束匹配、技能约束阻塞对、技能约束稳定匹配等定义。

定义1（偏好可接受对）在HSM(1，1，n，1)中，对于任意的Wi∈W，Ej∈E，若(Wi，Ej)∈W×E满足rij≠n+1 且tij≠m+1，则称(Wi，Ej)为偏好可接受对；否则，称(Wi，Ej)为偏好不可接受对。

在HSM(1，1，n，1)中，若家政服务人员所具备的技能能满足雇主需求，则称家政服务人员和雇主为技能可接受对；否则，称家政服务人员和雇主为技能不可接受对。

定义2（技能可接受对）在HSM(1，1，n，1)中，对于任意的Wi∈W，Ej∈E，若(Wi，Ej)∈W×E满足=1，则称(Wi，Ej)为技能可接受对；否则，称(Wi，Ej)为技能不可接受对。

定义3（可行技能约束匹配）设μ是HSM(1，1，n，1)中的一对一双边匹配，若对于任意的(Wi，Ej)∈μ都是偏好可接受对，且均为技能可接受对，则称匹配方案μ为可行技能约束匹配。

在匹配方案μ中，若家政服务人员Wi和雇主Ej均认为对方优于其在匹配方案μ中的匹配对象，且Wi满足Ej的服务技能需求，则称(Wi，Ej)是技能约束阻塞对。

定义4（技能约束阻塞对）在HSM(1，1，n，1)中，设家政服务人员与雇主的一对一双边匹配μ：W∪E→W∪E，在匹配方案μ中，对于任意的Wi∈W，Ej∈E，若偏好可接受对(Wi，Ej)同时满足以下条件：

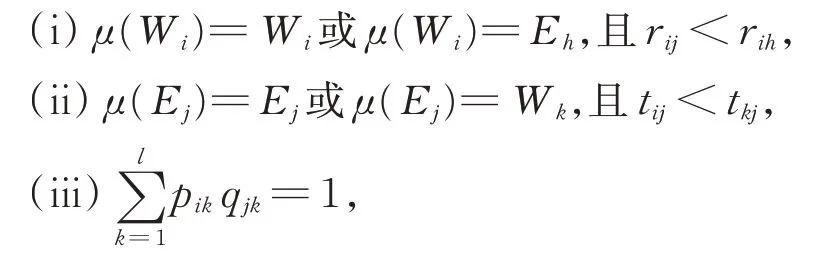
则称(Wi，Ej)是匹配方案μ的技能约束阻塞对。

定义5（技能约束稳定匹配）在HSM(1，1，n，1)中，设家政服务人员与雇主的一对一双边匹配μ：W∪E→W∪E，若匹配方案μ是可行技能约束匹配，且μ中不存在技能约束阻塞对，则称匹配方案μ为技能约束稳定匹配。

本文的目的是依据家政服务人员具备的技能P=[pik]m×l和雇主需要的技能Q=[qjk]n×l，以及家政服务人员和雇主的偏好信息R=[rij]m×n和T=[tij]m×n，采用双边匹配决策方法，获得双方的最优技能约束稳定匹配方案。

2 技能约束稳定匹配决策方法

2.1 家政服务人员和雇主的满意度计算

家政服务人员的满意度记为矩阵A=[αij]m×n，雇主的满意度记为矩阵B=[βij]m×n，i=1，2，…，m，j=1，2，…，n。在现实的家政服务人员与雇主的双边匹配过程中，由于受家政服务人员的心理行为影响，使得其对雇主的满意度与偏好排序值之间呈非线性关系。例如，对排在第1 位的雇主满意度可能为1，对排在第2 位的雇主满意度为0.95，对排在第3 位的雇主满意度为0.75，等等。类似地，雇主对家政服务人员的满意度与偏好排序值之间也存在类似的非线性关系。因此，为更准确地刻画家政服务人员和雇主的满意度，给出了家政服务人员Wi对雇主Ej满意度的计算式：

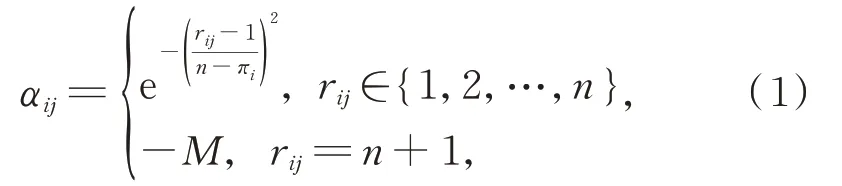
其中，M为足够大的正数，πi表示家政服务人员Wi不可接受的雇主数量。

雇主Ej对家政服务人员Wi的满意度计算式为

其中，ηj表示雇主Ej不可接受的家政服务人员数量。

在式（1）和式（2）中，家政服务人员和雇主的满意度是关于序值的严格单调递减非线性函数。如果家政服务人员Wi认为雇主Ej是可接受的，则0 ＜αij≤1；如果家政服务人员Wi认为雇主Ej是不可接受的，则αij=-M。雇主对家政服务人员的情况类似。

2.2 模型

依据家政服务人员的满意度A=[αij]m×n和雇主的满意度B=[βij]m×n，建立以家政服务人员和雇主总体满意度最大化为目标的数学模型。设xij为0-1 型决策变量，xij=1 表示家政服务人员Wi与雇主Ej形成匹配对；否则，xij=0。进一步，可构建0-1 型双目标整数规划模型，见式（3）～式（11）。

其中，式（3）和式（4）为目标函数，式（3）表示最大化家政服务人员的满意度，式（4）表示最大化雇主的满意度。式（5）～式（11）为约束条件，式（5）和式（6）为匹配数量约束，式（5）表示一名雇主最多需要一名家政服务人员，式（6）表示一名家政服务人员最多为一名雇主提供服务，式（7）为偏好可接受对约束，保证进行匹配的家政服务人员和雇主是偏好可接受的，式（8）为技能可接受对约束，保证在家政服务人员和雇主进行匹配时满足服务技能约束，式（9）为技能约束稳定匹配的约束条件，其中M是足够大的正数，式（10）保证只有可接受对才能成为技能约束稳定匹配，式（11）为决策变量取值约束。

对于任意的HSM(1，1，n，1)，设由式（3）～式（11）的可行解构成的稳定匹配集合为Ω，HSM(1，1，n，1)的所有稳定匹配构成的集合为U。

引理1在式（3）～式（11）中，任意一个可行解对应的匹配方案都是HSM(1，1，n，1)的技能约束稳定匹配，Ω⊆U。

证明设在式（3）～式（11）中，任意一个可行解为X=[xij]m×n，i∈{1，2，…，m}，j∈{1，2，…，n}，与可行解X对应的匹配方案为μ。将式（5）和式（6）作为匹配数量约束，以保证了家政服务人员与雇主的一对一双边匹配，即一名家政服务人员最多与一名雇主匹配，一名雇主最多与一名家政服务人员匹配。因此，μ是HSM(1，1，n，1)中的一对一双边匹配。式（7）和式（8）分别为偏好可接受对约束和技能可接受对约束，保证了μ是可行技能约束匹配。

为证明式（9）能够保证可行技能约束匹配μ是技能约束稳定匹配，可证明满足式（9）中的由任意的Wi∈W和Ej∈E组成的(Wi，Ej)不是技能约束阻塞对。若(Wi，Ej)是偏好不可接受对，即τij=1，则式（9）必成立，显然(Wi，Ej)不是技能约束阻塞对。若(Wi，Ej)是技能不可接受对，即=0，则式（9）必成立，显然(Wi，Ej)不是技能约束阻塞对。

下证若(Wi，Ej)是偏好可接受对和技能可接受对，则式（9）保证(Wi，Ej)不是技能约束阻塞对。

若(Wi，Ej)是偏好可接受对，即τij=0，则式（9）可化简为

引理2在HSM(1，1，n，1)中，任意一个技能约束稳定匹配都是式（3）～式（11）的可行解，即U⊆Ω。

证明设μ是HSM(1，1，n，1)中的技能约束稳定匹配方案。对于任意的Wi∈W，Ej∈E，若(Wi，Ej)∈μ，则令xij=1；否则，令xij=0。由于μ是一对一双边匹配，Wi和Ej无匹配对象或最多有一个匹配对象，因此，式（5）和式（6）成立。此外，由定义5 可知，μ中的匹配对均为偏好可接受对和技能可接受对，因此，式（7）和式（8）必成立。

下证技能约束稳定匹配μ对应的模型解满足式（9）。

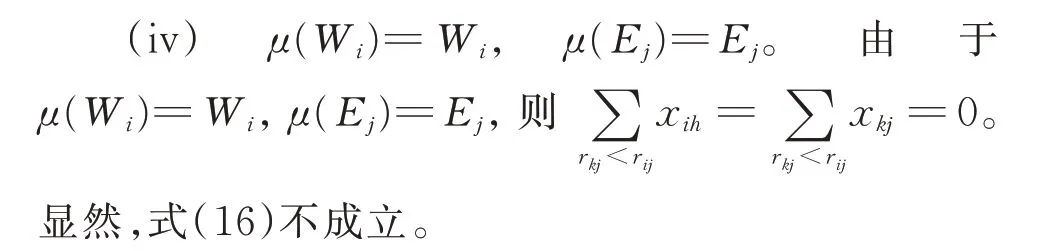
因此，在xij=0 且(Wi，Ej)是偏好可接受对和技能可接受对情形下，若(Wi，Ej)不是匹配方案μ的技能约束阻塞对，则式（9）必成立。由此可证，在技能约束匹配方案μ中，对于任意的Wi∈W，Ej∈E，均能使式（9）成立。

综上可知，任何一个技能约束稳定匹配都是式（3）～式（11）的可行解，即U⊆Ω。

证毕。

由引理1 和引理2，易得

定理1对于任意给定的HSM(1，1，n，1)，均有Ω=U。

2.3 模型求解

式（3）～式（11）是双目标的0-1 整数规划模型，本文采用ε-约束算法求解［20⁃21］。其基本思想是将其中1 个目标函数转换为约束条件，从而将双目标优化模型转换为单目标优化模型进行求解。

下面以目标函数Z2作为约束条件，说明ε-约束算法的具体流程。

令S为目标函数值集合，迭代步长为θ。

步骤5删除S中被占优的点，获得帕累托前沿，算法结束。

依据ε-约束算法理论，式（17）～式（25）的每个最优解都是式（3）～式（11）的帕累托解，因此，用上述算法通过不断迭代，可获得式（3）～式（11）的帕累托前沿。

3 算例分析

某专业、正规、服务管理体系完善的家政服务机构，可提供保姆、医疗陪护、月嫂、育婴师、钟点工、管家等家政服务。在一段时间内有8 名家政服务人员{W1，W2，…，W8}通过网络平台或中介门店寻找工作，每名家政服务人员都希望寻找一份合适的工作；有8 名雇主{E1，E2，…，E8}通过网络平台或中介门店寻求家政服务人员，每名雇主只雇佣一名家政服务人员。8 名家政服务人员掌握的技能包括做饭保洁、医疗陪护、月嫂、家庭护理、育婴护理5 种，分别用S1，S2，S3，S4，S5表示，每名家政服务人员掌握其中的一项或几项技能，8 名家政服务人员掌握的具体技能和8 名雇主需要的服务技能分别为

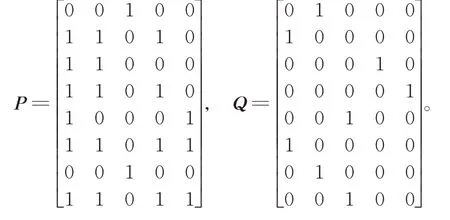
家政服务人员依据8 名雇主提供的工资待遇、食宿条件、工作环境等对各项指标进行总体评价并给出偏好排序值R=[rij]8×8。雇主依据8 名家政服务人员的工作经验、年龄、技能水平等对各项指标进行总体评价并给出偏好排序值T=[tij]8×8。

由式（1）和式（2），分别得到家政服务人员和雇主的满意度为

依据家政服务人员满意度和雇主满意度，建立式（3）～式（11）所示的双目标优化模型，并采用ε-约束算法求解模型。取迭代步长θ=0.1，以目标函数Z2为约束条件进行求解：

最后，对模型进行迭代求解，得到帕累托最优解和对应的目标函数值，见表1。

表1 技能约束稳定匹配方案Table 1 Skill constraints stable matching schemas

家政服务中介机构可根据实际情况从中选择最优稳定匹配结果。例如，若选择家政服务人员最满意的稳定匹配，则为方案μ1；若选择雇主最满意的稳定匹配，则为方案μ6；若选择双方满意度差值最小的稳定匹配，则为方案μ2。

4 结论

针对家政服务行业中家政服务人员与雇主的双边匹配问题，提出了一种基于稳定匹配理论的双边匹配决策方法，主要贡献体现在：（1）针对家政服务市场需考虑技能匹配约束的特点，给出了技能约束稳定匹配的定义；（2）给出了匹配双方序值与满意度的非线性计算式；（3）构建了考虑稳定性和满意度的技能约束匹配优化模型，并证明了模型的合理性。提出的决策方法弥补了已有家政服务人员与雇主双边匹配中未考虑匹配稳定性不足的问题，为解决现实家政服务行业中雇主的高解雇率和家政服务人员的高辞职率问题提供了一种新方法和新途径。