基于多隐层小波卷积极限学习神经网络的滚动轴承故障识别
2021-06-02黄重谦
黄重谦
(广西科技师范学院 机械与电气工程学院 , 广西 来宾 546199)
0 引言
滚动轴承是煤矿旋转机械的重要部件,其工作状态直接影响着整机的工作性能。因此,及时对煤矿旋转机械滚动轴承进行状态监测与故障识别,具有重要意义[1]。煤矿旋转机械工作环境恶劣,实际采集到的滚动轴承振动信号受环境噪声干扰明显,且由于传递路径比较复杂,信号呈现出明显的非线性和非平稳性,导致轴承故障特征提取较困难。
多隐层自动编码网络[2]能自动地从滚动轴承振动信号中学习有价值的特征,克服了传统基于“人工特征提取+模式识别”方法受主观影响大的缺陷[3],在滚动轴承故障识别领域取得了较大突破。文献[4]在缺少滚动轴承故障信息的情况下,利用多隐层玻尔兹曼网络取得了较高的识别准确率;文献[5]提出的融合多隐层自动编码网络能更有效、更稳健地对滚动轴承的多种故障进行识别。自动编码网络[6]不需要标记数据,其训练过程为非监督过程,因此,可将自动编码网络的思想应用到极限学习网络[7],得到极限学习自动编码器(Extreme Learning Auto-Encoder,ELAE)。利用ELAE的特征表达能力,将其作为多隐层极限学习自动编码神经网络的基本单元[8]。但ELAE为全连接网络,需要学习的参数众多,训练时间较长,学习到的信号特征的平移不变性较差,受噪声影响较大,且标准ELAE使用sigmoid激活函数,泛化能力较弱[9]。针对上述问题,本文提出一种基于多隐层小波卷积极限学习神经网络(Multi Hidden Layers Wavelet Convolution Extreme Learning Neural Network,MHLWCELNN)的滚动轴承故障识别方法,实验结果表明该方法具有较高的可行性和有效性。
1 多隐层小波卷积极限学习神经网络
1.1 一维卷积神经网络
一维卷积神经网络(1D-CNN)[10]具有局部连接和权值共享特性,可有效降低网络过拟合风险,其工作原理如图1所示。

图1 1D-CNN工作原理Fig.1 The working principle of 1D-CNN
以卷积层为例,设输入的轴承振动信号为x,则卷积层输出为
Ccn=f(x*Wcn+bcn)
(1)
式中:Ccn为输出特征图;f为激活函数;“*”为卷积符号;Wcn为滤波器权重;bcn为偏置向量。
1.2 自动编码器
1D-CNN为有监督模型,需要大量的带标签样本,而实际工业应用中轴承振动信号无标签样本多。自动编码器(Auto-Encoder,AE)为无监督模型,训练过程只需要无标签样本,AE结构如图2所示,包括输入层、隐层和输出层,其单元个数分别为m,L,m。

图2 AE结构Fig.2 The structure of AE
AE隐层的输出h为
h=sigmoid(W·x+b)
(2)
式中:W为隐层的权重;b为隐层的偏置。
AE输出层的输出y为
y=sigmoid(W′·h+b′)
(3)
式中:W′为输出层的权重;b′为输出层的偏置。
AE的损失函数E一般为
(4)

AE的参数更新策略为
(5)
式中:R为AE训练时的迭代次数;η为AE的学习率。
AE为全连接网络,训练参数较多,且其激活函数为sigmoid函数,泛化能力较弱,另外,AE的参数训练采用BP算法,很容易陷入局部最优。
1.3 小波卷积极限学习神经网络
极限学习机(Extreme Learning Machine,ELM)是一种单隐层神经网络,通过求解矩阵的Moore-Penrose广义逆,进而确定输出权重,训练速度较快。因此,综合1D-CNN,AE,ELM和小波函数的优势,构造小波卷积极限学习神经网络(Wavelet Convolution Extreme Learning Neural Network,WCELNN)。
(1) 将AE和ELM结合,构造ELAE。ELAE为3层无监督网络,其结构与图2类似。ELAE隐层的输出与AE隐层的输出相同,ELAE输出层的输出为
y=hT·β
(6)
式中β为隐层到输出层的输出权重向量。
ELAE的优化函数为
(7)
(8)
式中:I为单位矩阵;A为常数;H为隐层矩阵。
(2) 将ELAE和1D-CNN结合,构造卷积极限学习神经网络(Convolution Extreme Learning Neural Network,CELNN),其结构如图3所示。
CELNN隐层第k个节点的输出hk为
hk=sigmoid(Wk*x+bk)
(9)
式中:Wk为隐层第k个节点的卷积核权重矩阵;bk为隐层第k个节点的偏置。
(3) 将CELNN和小波函数结合,构造WCELNN。由于高斯小波函数在时域、频域均具有良好的分辨率,故激活函数使用高斯小波函数:
(10)
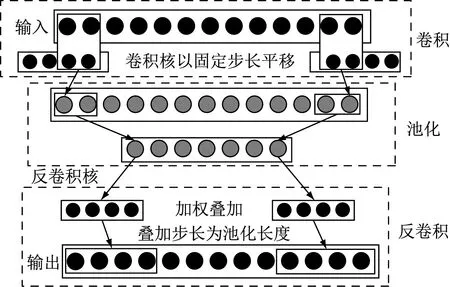
图3 CELNN结构Fig.3 The structure of CELNN
式中t为时间。
WCELNN隐层第k个节点的输出hk为
hk=ψ[(x*Wk-ck)./ak]
(11)
式中:ak和ck分别为小波节点的尺度向量和平移向量;“./”表示按元素相除。
WCELNN输出层的输出为
(12)

根据ELM训练方法,WCELNN的优化函数可表示为
(13)
(14)
WCELNN不使用BP算法,其输出权重计算较为简单,运算速度较快。
2 基于MHLWCELNN的滚动轴承故障识别
MHLWCELNN堆叠多个WCELNN,能进一步提高网络学习到的特征的质量。利用无标签的滚动轴承振动信号样本训练第1层WCELNN,得到第1隐层特征;将第1隐层特征输入第2层WCELNN,得到第2隐层特征;依此类推。MHLWCELNN结构如图4所示。

图4 MHLWCELNN结构Fig.4 The structure of MHLWCELNN
基于MHLWCELNN滚动轴承故障识别步骤如下:① 采集不同工况下的滚动轴承振动信号并进行样本划分。② 将训练样本输入MHLWCELNN进行训练。③ 使用测试样本对训练好的网络进行测试。
3 实验验证:基于XJTU-SY数据集
3.1 实验数据描述
为验证MHLWCELNN的有效性,以XJTU-SY滚动轴承数据集[11]为对象进行实验。实验轴承为LDK UER204滚动轴承。限于计算资源,在XJTU-SY数据集中选取9种不同的轴承工况数据:正常(a,b)、内圈轻微故障(c)、内圈中度故障(d)、内圈重度故障(e)、外圈轻微故障(f)、外圈中度故障(g)、外圈重度故障(h)、滚珠轻微故障(i)、滚珠中度故障(j),最后得到每种工况下的8 000个样本,随机选取70%作为训练样本,其余作为测试样本,每个样本1 024个采样点,即1 024维。
各种工况下的轴承时域信号如图5所示,可见振动信号受噪声干扰严重,难以进行有效区分。

(a) 工况a

(c) 工况c
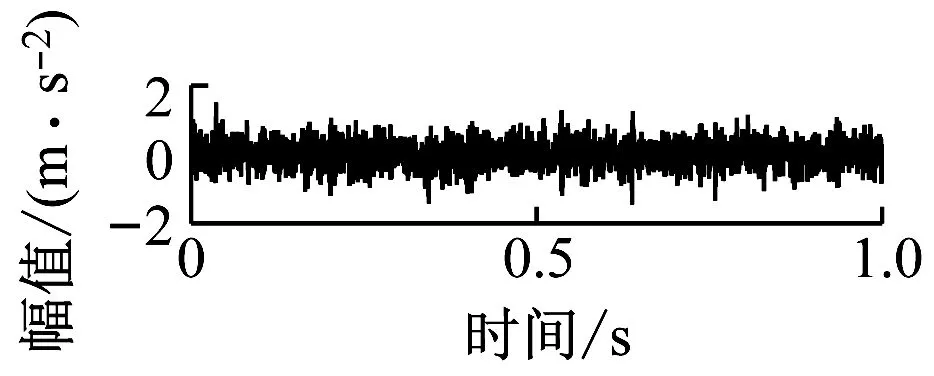
(e) 工况e

(g) 工况g

(i) 工况i
3.2 故障识别与分析
为验证MHLWCELNN的优势,采用多隐层自动编码神经网络(Multi Hidden Layers Auto Encoder Neural Network,MHLAENN)、多隐层稀疏自动编码神经网络[12](Multi Hidden Layers Sparse Auto Encoder Neural Network,MHLSAENN)、多隐层降噪自动编码神经网络[13](Multi Hidden Layers Denoising Auto Encoder Neural Network,MHLDAENN)、多隐层收缩自动编码神经网络[14](Multi Hidden Layers Contractive Auto Encoder Neural Network,MHLCAENN)和多隐层极限学习自动编码神经网络(Multi Hidden Layers Extreme Learning Auto Encoder Neural Network,MHLELAENN)等方法进行对比分析,输入均为1 024维信号样本,各网络结构均为1 024-512-256-128-64-32-10。共进行10次试验,不同方法的识别结果见表1。
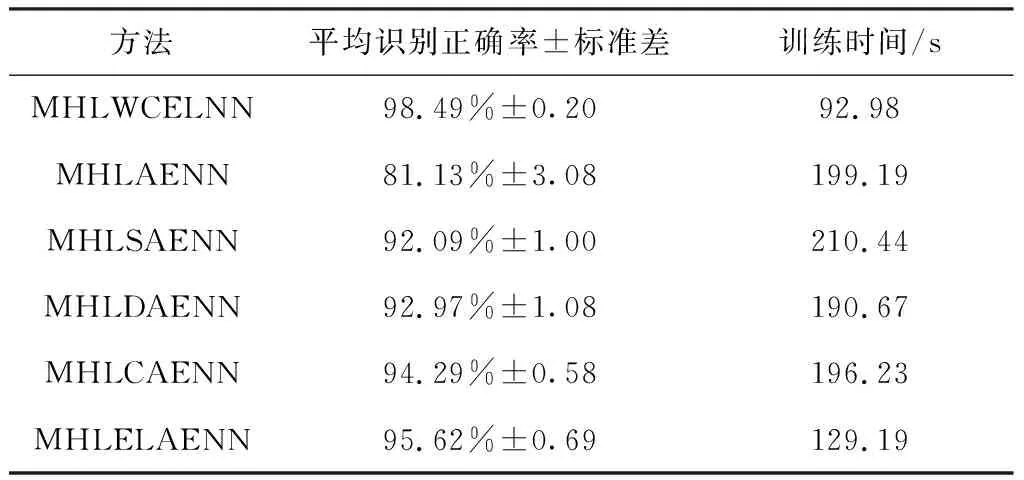
表1 不同方法的识别结果(基于XJTU-SY数据集)Table 1 Identification results of different methods (based on XJTU-SY data set)
由表2可知,MHLWCELNN具有更高的识别准确率和更小的标准差,能较为稳定地识别出滚动轴承的故障类型。这几种方法中,MHLAENN方法的故障识别率最低,仅81.13%;MHLSAENN加入了稀疏项限制,可捕捉输入数据中较重要的信息;MHLDAENN加入了降噪机制,一定程度上提高了网络对噪声的鲁棒性;MHLCAENN加入了收缩项限制,使网络对输入信号的小扰动具有一定的抗干扰性。MHLSAENN,MHLDAENN和MHLCAENN较MHLAENN都取得了更高的故障识别率。MHLELAENN 利用ELAE优秀的特征表达能力和快速的网络收敛能力,故障识别率达到了95.62%,训练时间仅129.19 s。本文提出的MHLWCELNN采用局部连接和权值共享机制,大大减少了需要学习的参数,故训练时间较短,受噪声影响较小,且使用小波激活函数,具备一定的时频聚焦特性,能有效学习轴承振动信号的时频特征,故障识别率高于其他方法。
3.3 基于不平衡数据集的故障识别率
为验证MHLWCELNN对不平衡故障样本的有效性,设计了一种不平衡数据集,正常与故障工况的训练样本比例为8 000∶4 000,实验共进行10次,采用MHLCAENN,MHLELAENN方法作为对比。
准确率、召回率、F1值作为评估指标,经常被用到分类效果的评测上。其中F1值可在准确率和召回率之间取得平衡,让两者同时达到最高。因此,采用F1值定量评价3种方法基于不平衡数据集的分类效果,F1值计算公式为
(15)
式中:F1值在[0,1]之间,0代表最差,1代表最好;P为准确率;Q为召回率。
不同方法的F1值见表2。

表2 不同方法的F1值Table 2 F1 values of different methods
由表2可知,MHLWCELNN的F1值较高,验证了MHLWCELNN对不平衡数据集的有效性。
3.4 激活函数对MHLWCELNN识别率的影响
激活函数对MHLWCELNN的故障识别率有一定影响,采用不同激活函数时MHLWCELNN的识别率见表3。从表3可知,高斯小波、Morlet小波和Mexican hat小波的故障识别效果好于其他激活函数,高斯小波在时域、频域均有较高的分辨率。
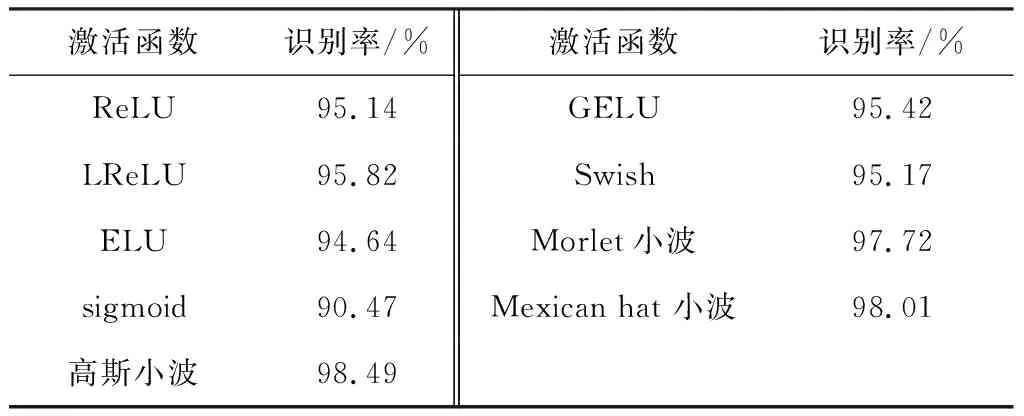
表3 不同激活函数对MHLWCELNN识别率的影响Table 3 Effects of different activation functions on identification accuracy of MHLWCELNN
4 实验验证:基于西储大学数据集
4.1 实验数据描述
以西储大学轴承数据集为对象,在测试轴承上通过电火花加工形成不同故障尺度的凹坑,限于计算资源,从西储大学轴承数据集中选取7种不同的轴承故障工况数据:正常(A)、内圈轻微故障(B)、内圈中度故障(C)、外圈轻微故障(D)、外圈中度故障(E)、滚动体轻微故障(F)、滚动体中度故障(G),每种工况的样本数量为8 000。7种轴承故障工况下的时域信号及相应的频域信号如图6所示。从图6可知,故障信号受噪声干扰严重,难以直接从时域图中对滚动轴承的故障类型及程度进行有效区分。

(a) 工况A,时域信号

(c) 工况B,时域信号
(e) 工况C,时域信号

(g) 工况D,时域信号

(i) 工况E,时域信号

(k) 工况F,时域信号
(m) 工况G,时域信号
4.2 故障识别与分析
采用MHLWCELNN等6种方法进行对比实验,结果见表4。
从表4可知,MHLWCELNN具有更高的识别准确率和更小的标准差,能较为稳定地识别出滚动轴承的不同故障类型,进一步验证了MHLWCELNN的优越性。

表4 不同方法的识别结果(基于西储大学数据集)Table 4 Identification results of different methods (based on the data set of Western Reserve University)
4.3 训练集占比对故障识别准确率的影响
训练集和测试集的样本比例对MHLWCELNN的轴承故障识别准确率有一定影响。若训练集样本比例过低,会引起MHLWCELNN欠拟合;若训练集样本比例过高,则会引起MHLWCELNN过拟合。欠拟合和过拟合均会影响网络的识别准确率。训练集样本占比为60%~90%时,MHLWCELNN的故障识别率如图7所示。
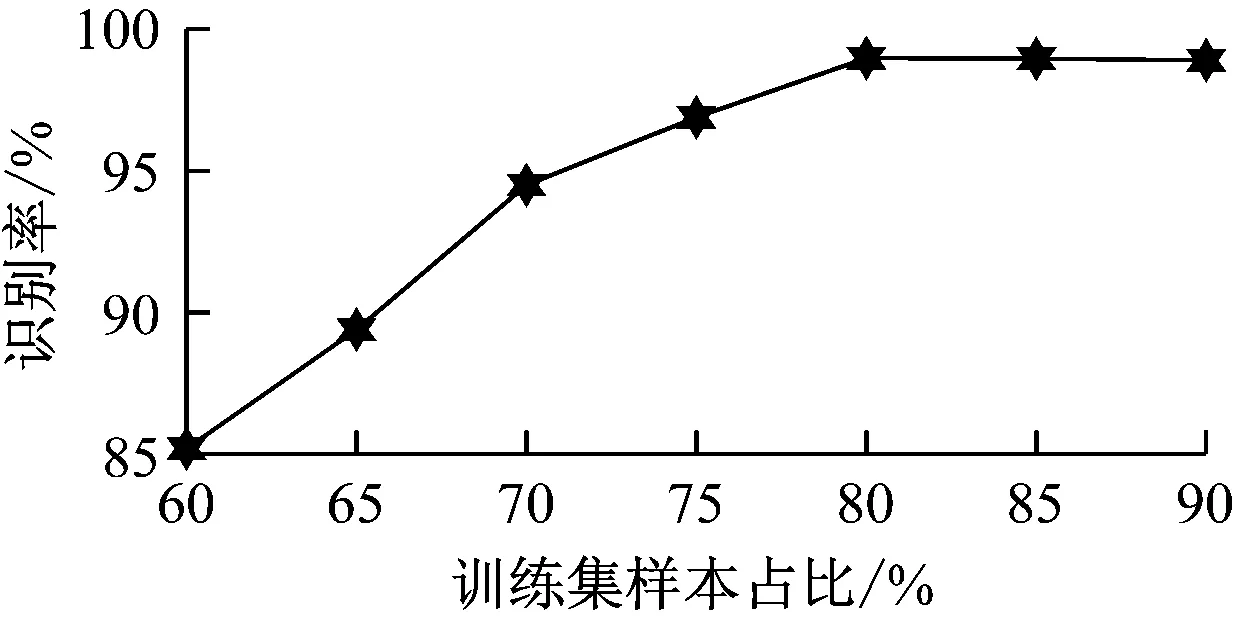
图7 训练集样本占比对故障识别准确率的影响Fig.7 Effect of proportions of training set on fault identification accuracy
从图7可知,训练集样本占比为60%~80%时, MHLWCELNN的故障识别率随训练集样本所占比例增加而增加;当训练集样本占比超过80%时,故障识别率不再上升,故设置训练集样本占比为80%较合适。
5 结论
提出了一种基于MHLWCENN的滚动轴承故障识别方法,该方法学习能力和泛化能力强,且具有局部连接特性和权值共享特性,更适用于非线性和非平稳性轴承振动信号。基于XJTU-SY数据集和西储大学数据集的实验结果表明:
(1) 与MHLAENN,MHLSAENN等相比,MHLWCELNN能有效学习轴承振动信号的时频特征,具有更高的识别准确率和更小的标准差。
(2) MHLWCELNN的F1值高于MHLCAENN,MHLELAENN,验证了MHLWCELNN对不平衡数据集的有效性。
(3) 高斯小波、Morlet小波和Mexican hat小波的故障识别效果好于其他激活函数,高斯小波在时域、频域均有较高的分辨率。
(4) MHLWCELNN的故障识别率随训练集样本所占比例增加而增加,当训练集样本占比超过80%时,故障识别率不再上升,故设置训练集样本占比为80%较合适。
