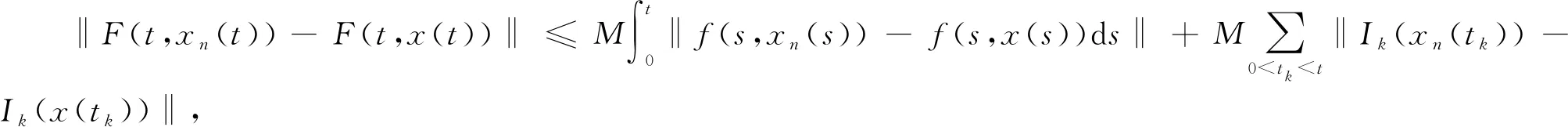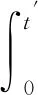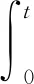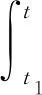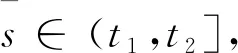中立型变时刻脉冲发展方程mild解的存在唯一性

陶 书，马维凤，陈鹏玉

(西北师范大学数学与统计学院，甘肃 兰州 730070)

1 引言与研究背景

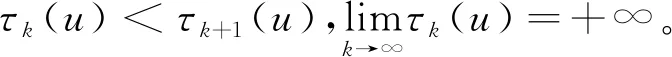
N(t):Ω→Ω，u→N(t)u=u+Ik(u)

其中Ik:Ω→Ω，进而脉冲时刻不固定的脉冲微分方程可用如下模型：

(1)

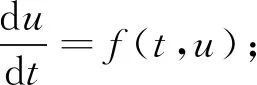
近年来，脉冲微分方程理论在种群动力系统，传染病动力学系统，微生物模型等领域应用广泛[2-3]。一般来说，脉冲微分方程系统的解是分段连续的，不连续点发生脉冲现象。对模型(1)来说，不同的解在不同时刻发生间断，这个特征使其研究起来比较困难，正因为如此，脉冲微分方程引起了国内外众多学者的研究兴趣[4-10]，Marlene等应用上下解的单调迭代方法给出了问题⑴解的存在性条件[6]；Benchohra等利用Schaefer不动点定理研究了问题⑴解的存在性[7]；Mouffak研究了含中立型脉冲微分方程初值问题解的存在性[8]。在半群理论下，脉冲发展方程的研究也有了重要突破，有限维空间中的基本理论参见[2-3]，此外，彭云飞等研究了脉冲发展方程初值问题mild解的存在性[9-10]。

在上述理论和结果的启发下，本文Banach空间E中讨论如下中立型变时刻脉冲发展方程初值问题

(2)

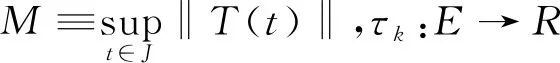
2 预备知识及引理

设E是按范数‖·‖构成的Banach空间，记C(J,E)是定义于J取值于E的连续函数全体按最大值范数‖u‖c:=max{‖u(t)‖:t∈J}构成Banach空间，定义PC(J,E)={x:J→E,x(t)在J′上连续,在每个τk(x(t))点左连续且x(t+)=x(t)+Ik(x(t))}，其按上确界范数‖x‖PC=sup{‖x(t)‖:t∈J}构成Banach空间。

定义2.1若f:J×E→E满足条件：

(ⅰ)对所有的x∈E，f(t,x)关于t可测；

(ⅱ)对几乎所有的t∈J，f(t,x)关于x连续，即存在ρ>0，对任意的x,y∈E，有

‖f(t,x)-f(t,y)‖≤ρ‖x-y‖

则称f是L1-Carathéodory函数。

定义2.2若x:[0,a]→E满足下列条件：

(ⅰ)对任意t∈[0,a]，(t,x(t))∈J×E；

(ⅱ)对任意t∈[0,a]，t≠τk(x(t))(k∈Z+)，函数x(t)是连续的，且

(ⅲ)若t∈[0,a]，t=τk(x(t))，t≠0，函数x(t)左连续，即x(t+)=x(t)+Ik(x(t))，

且对每个j∈Z和δ>0，s≠τj(x(t))，t

tk)Ik(x(tk))，t∈J

是初值问题(2)的mild的解。

引理2.3(Krasnoselskii不动点定理)设E是Banach空间，Ω⊂E是有界凸闭集，若T,S:Ω→E满足：(ⅰ)对任意的x,y∈Ω，有Sx+Ty∈Ω；(ⅱ)算子S是压缩的；(ⅲ)T在Ω上是全连续的。则T+S在Ω内至少有一个不动点。

3 主要结果

对任意0

(H1)f是L1-Carathéodory函数，且存在r>0，使得对每个x∈Ωr及t∈J，有

‖f(t,x)‖≤p1‖x‖+p0

其中p1，p0为常数；

(H2)存在常数Lg≤1及r>0，使得对任意的0≤t1≤t2≤a，x,y∈Ωr，有

g(t1,x)≤g(t2,x)，‖g(t,x)-g(t,y)‖≤Lg‖x-y‖，

(H3)函数τk∈C(J,E)，k=1,…,m是不增函数，且存在r>0，对任意的x∈Ωr，有

0<τ1(x1)<τ2(x2)<…<τm(xm)

(3)

(H4)存在r>0对所有的t∈J，x∈Ωr，有

定理3.1若假设条件(H1)～(H5)成立，且

(4)

则初值问题(2)在[0,a]上有唯一mild解x(t)∈PC(J,E)。

证明首先，定义积分算子F:PC(J,E)→PC(J,E)：

(5)

和算子S:C(J,E)→C(J,E)：

(Sx)(t)=g(t,x(t))-T(t)g(0,x0)，t∈J

(6)

令H=F+S，则问题(2)的解等价于算子H的不动点。下证H有不动点。

具体分为以下三步：

(Ⅰ)存在r>0，对任意的x,y∈Ωr，Sx+Fy∈Ωr，反设不成立，对任意的r>0，x,y∈Ωr，有‖Sx(t)+Fy(t)‖>r。由条件(H2)，(H1)和(H5)可知，对任意的x,y∈Ωr，t∈J，有

x(t))-T(t)g(0,x0)‖+‖T(t)x0‖+

其中‖g(a,x0)-g(0,x0)‖=G，从而

r<‖(Sx)(t)+(Fy)(t)‖≤(Lg+Map1+mML)r+(Lg+M)‖x0‖+Map0+MG

上式两端同时除以r，且当r→∞时取极限，得1

(Ⅱ)证明S是压缩的，存在r>0，对任意的x,y∈Ωr，t∈J，有

‖(Sx)(t)-(Sy)(t)‖=‖g(t,x(t))-g(t,y(t))‖≤Lg‖x-y‖

(Ⅲ)证明F全连续。设{xn}是一个收敛序列，且在PC(J,E)中收敛到x，则

‖F(t,xn(t))-F(t,x(t))‖PC≤M‖f(s,xn(s))-f(s,x(s))‖L1+mML‖xn-x‖PC→0(n→∞),

故‖F(t,xn(t))-F(t,x(t))‖→0(n→∞)。且存在r>0，对任意的x∈Ωr，同(Ⅰ)用反证法有

因此F:Ωr→Ωr连续。对任意的ε>0，令

对任意的x∈Ωr，t∈J，由(H1)得

M(p1‖x‖+p0)a≤M(p1r+p0)ε

由T(t)的紧性知，(FεΩr)(t)={(Fεx)(t):x∈Ωr}为E中的相对紧集，由(5)式知，存在r>0，对任意的x∈Ωr，t∈J，有

即(FεΩr)(t)为(FΩr)(t)中的相对紧的M(p1r+p0)ε网，故(FΩr)(t)为E中的逐点相对紧集。

另一方面，存在r>0，对任意的x∈Ωr，t′,t″∈J，t′

tk)Ik(x(tk))‖≤‖T(t″)-T(t′)‖‖x0‖+

由T(t)(t≥0)的等度连续性可知，上式右端趋于零(当t″→t′时)，且与t′与t″的取值无关，从而(FΩr)(t)={(Fx)(t):x∈Ωr}等度连续，故由Arzela-Ascoli定理可得FΩr相对紧，从而F:Ωr→Ωr全连续。

综上，H在PC(J,E)上存在不动点。定义方程

rk,1(t)=τk(x1(t))-t，t≥0

由条件(H3)知rk,1(0)≠0，t∈J，k=1,…,m。若rk,1(t)≠0，k=1,…,m，则t≠τk(x1(t))，t∈J，k=1,…,m，那么

是初值问题(2)的mild解。

当t∈J，r1,1(t)=0时，由于r1,1(0)≠0且r1,1是连续的，故存在t1>0，使得

r1,1(t1)=0，r1,1(t)≠0，t∈[0,t1]

因此，由条件(H3)可得，rk,1(t)≠0，t∈[0,t1]，k=1,…,m。

定义方程

rk,2(t)=τk(x2(t))-t，t>t1

若rk,2(t)≠0，t∈(t1,a]，k=1,…,m，则

是初值问题的(2)的mild解，且满足

当r2,2(t)=0，t∈(t1,a]时，由条件(H3)可知

由于r2,2是连续的，故存在t2>t1，使得r2,2(t2)=0，r2,2(t)≠0，t∈(t1,t2]，故由条件(H3)可得

rk,2(t)≠0，t∈(t1,t2]，k=2,…,m

L1(t)=τ1(x2(t)-g(t,x2(t)))-t

(7)

由条件(H3)得

因此由(7)式得非负最大值点s1∈(t1,t2]，有

由于

则

与(3)式矛盾!从而r1,2(t)≠0，t∈(t1,t2]。

归纳得，初值问题(2)在(tm,a]上存在mild解，记为xm+1(t)∈PC(J,E)，且有如下形式:

构造函数x(t)如下:

显然x(t)∈PC(J,E)，且满足定义2.1的条件，因此，

tk)Ik(x(tk))，t∈J

为初值问题(2)在[0,a]上的mild解。

下证唯一性，设x,y∈PC(J,E)均为初值问题(2)的解，对任意的t∈(tk,tk+1]，有

mML‖x(t)-y(t)‖PC

对上式取上确界，可得

故

‖x(t)-y(t)‖PC≤

令z(t)=‖x(t)-y(t)‖，从而由Bellman不等式可知，在(tk,tk+1]上有z(t)=0，即x(t)=y(t)。因此，初值问题(2)在[0,a]上有唯一解x(t)∈PC(J,E)。