中国证券市场多元金融上市公司的复杂网络动态拓扑结构研究

牛晓健，刘红怿

(复旦大学 经济学院，上海 200433)

一、引言

当代金融发展的历史是一部金融创新的历史。人类社会在经历了漫长的易物交易阶段后，就开始了不断金融创新的历程，从货币的演变到纸币的使用，再到银行等金融机构的创建和初级证券的发行，人类为了逃避监管或为谋取利润降低风险而创造出越来越复杂的金融衍生产品。金融创新的进程中，资金流通速度不断加快，与之相伴的是各类金融机构的联系也愈发紧密，大有“牵一发而动全身”之势。金融危机与此相伴相生，从1929年的大萧条、1987年的股市“黑色星期一”，到1997的亚洲金融危机，再到2007年美国次贷危机，金融创新驱使下的金融机构的杠杆率居高不下。在相对稳定期利润放大的同时，也在波动期增加了风险，系统性金融危机在全世界范围内出现频率增高，破坏性增强。随着全球化进程的逐步推进，更多的国家与地区加入到了全球金融市场中，渐渐放开了对投资的资本限制和对金融机构的监管标准，大型金融机构在全球布局和国际游资在全球新兴市场的大量涌入和突然撤出，会给这些尚没有完善监管法律法规和相应人才储备的国家和地区带来快速的繁荣，也会令这繁荣瞬间破灭。在来去迅捷的游资的影响下，金融系统中的“蝴蝶效应”也更加强烈，一家地区银行的违约有可能演变成导致全国金融市场乃至全球金融市场动荡的大风险，而金融系统受到破坏也往往会影响到实体经济，造成国内生产总值增速放缓。各个金融监管机构再也不能只是“管好自己”的工作，系统性金融风险也应进入管理者的视野。与之相应的是如何防止一场突发性金融危机从局部动荡向整体崩盘的发展，这也已经成为世界各国金融管理的重点。尽可能地对金融系统中的各类金融机构的内在联系有一个客观总体的研究，是做好系统性金融风险防范的前提。

近年来在自然科学领域兴起的复杂网络理论被逐渐引入对金融风险的研究，该理论在研究金融风险的传播机制、危机的传导过程、风险压力测试等方面取得了大量有价值的成果。借鉴该理论的研究方法，本文对2009年和2019年两个年度的多元金融类上市公司股票进行不同阈值下的复杂网络建模，以单只股票为网络节点，股票收益率时间序列相关性为边的权重，通过控制变量法进行检验，分析在这段时间跨度内的网络结构变迁，探讨可能的原因，并同时结合公司间的实际关联，在此基础上为股票市场的投资和监管提出相应的政策建议。

二、文献综述

20世纪50年代末，两位匈牙利数学家Erdös和Rényi提出了第一个复杂网络模型——ER随机图模型，其网络的构成方法是任意两节点之间都以某一概率P随机连边,这也拉开了复杂网络理论的系统性研究的序幕。在这之后的40年里，ER随机图模型一直是研究复杂网络的基本模型。在20世纪末，对复杂网络的研究发生了重要的转变，拥有大量节点和边的实际网络渐渐成为主要研究对象。Watts和Strogatz提出了小世界网络模型，小世界网络模型介于规则网络和随机网络之间，通过将规则网络中的每条边以一个给定的概率p连接到一个新节点上构造而成[1]。Barabási和Albert提出了BA网络模型即无标度网络，在网络的构造中引入了增长性和择优连接性：增长性指网络中不断有新的节点加入进来，择优连接性则指新的节点进来后优先选择网络中度数大的节点进行连接[2]。BA网络是无标度网络(scale-free networks)模型，其节点度服从幂律分布。

Watts等人提出的“小世界”效应和Barabási等人提出的“无标度”性质拉开了复杂网络研究的新纪元，复杂网络的研究在过去几年中得到了迅速发展，其研究者来自图论、统计物理、计算机、生态学、社会学以及经济学等各个不同领域。对复杂网络的定性特征与定量规律的深入探索、科学理解以及可能的应用，已成为网络时代复杂科学研究中一个极其重要的挑战性课题。

建立在规则网络和随机网络基础上的复杂网络理论自诞生以来，就因为其简洁直观性和对现实模拟的贴近被广泛应用于各大学科领域，尤其是在金融市场这样一个体积大、联系复杂而紧密的系统中。Kim等人通过建立股票价格变化相关性加权网络，发现网络中节点影响能力的绝对值分布服从无标度模式[3]。Bonanno等人认为复杂网络可以用来过滤噪声，网络的拓扑特性显示了金融网络的实际相关特性[4]。Lee等人提出了阈值的概念，认为阈值在0.4和0.6之间时，复杂网络具有无标度性，并通过建立韩国证券市场股票价格相关性的复杂网络进行了实际验证[5]。

自朱涵将小世界、集团化和无标度等复杂网络的概念向国内学界介绍以后[6]，我国在复杂网络理论的应用上有了显著的进展[7]。近年来国内学者开始将复杂网络理论应用在中国证券市场上，李平、汪秉宏等人探索了港股恒生指数的波动类型[7]。黄伟强，庄新田等人以上证180指数和深证100指数成份股为研究标的，分析了沪深市场股票关联网络的拓扑性质和聚类结构[8]。兰旺森，赵国浩研究了中国股市煤炭、电力板块内部的复杂网络结构，发现其具有无尺度特性，且分析了其中的核心节点，抽取了一个对整体网络影响极大的高度耦合的中心网络[9]。宋宜飞，邵峰晶等人建立了上海A股股票市场的无向网络和有向网络，发现其具有小世界特性，并通过社团分析发现股票网络中存在较明显的社团结构，且同一板块股票关联性较强，可以解释证券市场中的股票同涨同跌现象，同时，一些在网络中占据核心地位的股票会很容易将自身的价格波动传递到网络中的其他股票[10]。

目前针对国内证券市场的复杂网络研究显示，股票市场的复杂网络具有明显的小世界特性，且往往具有社团化结构，社团内公司股票价格同涨同跌现象明显，一些在网络拓扑结构中重要节点的公司的股票价格会更容易影响其他股票，由核心公司股票组成的局部网络往往已经涵盖了整体网络的大部分信息，为现实中“指数成分公司”的选择提供了复杂网络理论基础上的验证。但值得注意的是，目前关于证券市场复杂网络结构的变动多是一个时间段内的稳态研究，大多是研究网络拓扑结构的静态属性，对于同一类型网络在较长时间跨度上的结构变动则研究较少，而实际经济生活中各家公司的经营状况处于一个动态变化的过程中，这些基本面的变化势必影响到其股票价格的变化，对复杂网络结构特性的变化分析，有助于我们更好地理解现实中的网络动态结构，同时也为证券市场的投资者和相关监管部门提供一个新的视角。

三、多元金融类上市公司的复杂网络构建

近年来随着金融脱媒化的不断演进，非传统类金融公司在企业的投融资、金融市场中发挥越来越重要的作用，为探索非传统金融类上市公司的网络结构，本文的研究选取在A股上市的多元金融类公司，主要包括非银行、保险、证券类金融公司，这些主营业务是为实体经济公司提供金融服务，如信托、融资租赁、小额贷款、供应链金融、股权投资等，有一些也同时开展自己的实体业务和金融投资业务。选择的背景是考虑到国内已经有多项针对传统金融如商业银行、证券公司、保险公司等的复杂网络研究，都发现了其内部的小世界特性，而对非传统类金融上市公司的研究相对较少，但是其在我国投融资体系中作用不可小觑，不论是投融资规模还是数量都呈现快速增长态势，其在系统性风险传播中的作用也在逐步增强。

本文数据来源是在东方财富网得到“多元金融”类在2009年度和2019年度上市公司名册，在Wind数据库中获得其在相应年度的价格数据时间序列，删去年度内新上市的公司和价格数据缺失10日以上的公司。2009年度共有16家上市公司，244个交易日；2019年度25家上市公司，244个交易日。通过中值插入法补全时间序列后，以收盘价计算股票对数收益率时间序列的相关性：

R(t)=lnP(t)-lnP(t-Δt)

取Δt=1 day，计算股票i与股票j的相关性为：

当相关性超过阈值时，则认为以这两家公司为节点的边存在，否则不存在，相关性越大，边的权重越大。设定两个不同阈值0.4和0.5。将相关性超过阈值的组合的其中一家公司命名为source，另一家公司为target，并将相关性的数值作为weight。将处理所得数据序列导入Gephi软件用Force Atlas 2(1)力引导布局，通过模拟物理中的引力和斥力，使得网络中的节点和边达到力平衡状态，产生图紧凑可读性强。算法进行无向加权复杂网络建模。

文中各图中，不同度数的节点颜色不同，节点的大小与其度数成正比，边的粗细代表其权重(即连接的两个节点公司股票的相关度)。

图1、图2是当阈值=0.5时的复杂网络拓扑结构示意图。

图1 阈值=0.5时2009年度多元金融公司网络拓扑结构

四、多元金融类上市公司复杂网络动态拓扑结构研究

(一)网络结构统计特性异同

表1为阈值设定为0.4时对2009和2019年的多元金融板块复杂网络的特性统计，表2为阈值设定为0.5时的特性统计。从两表易知多元金融板块的复杂网络随着时间推移，呈现出连接愈发紧密的趋势。

表1 阈值=0.4时的复杂网络统计特性

表2 阈值=0.5时的复杂网络统计特性

由于公司节点数目的变化，暂不考虑平均度和平均加权度的差异，在阈值=0.4时，两年度的网络统计特性没有太大差异，而当阈值为0.5时，二者在图密度和平均聚类系数两项上出现了较大差别，2019年度的复杂网络节点间相互连通性更强，网络中的平均路径更短。

如上复杂网络拓扑结构的变化，我们结合多元金融类上市公司的经营环境来寻求现实可能的原因。早在2009年，国内统一的金融监管框架尚未建立，在金融领域“九龙治水”的情况下，金融业呈现分业经营、分业监管的格局，尤其是非传统金融领域，当一个金融子行业出现风险问题，采用的政策举措可能是“一刀切”，进而限制该子行业领域所有的公司发展，例如信托业历史上就存在若干这样的时期。而这种政策措施会有利于其他金融子行业，企业投融资的需求是长期存在的，每当一个投融资渠道不顺畅，就会转向其他渠道，因此可能出现这些金融子行业“此消彼长”的发展态势，其业绩会出现相应的差异化，而这逐步体现在其公司股票价格上。例如，对于信托行业的严监管可能导致银行表外业务、委托贷款以及金融租赁市场、非标金融产品市场的快速发展，造成金融监管“按下葫芦浮起瓢”，监管的实际效果大打折扣。在复杂网拓扑络构上体现为各家上市公司股票价格的关联性不是很强，甚至还会出现背离情况。

近年来，这一长期困扰金融监管部门的痼疾得到了有效解决，2018年4月27日《关于规范金融机构资产管理业务的指导意见》(以下简称《资管新规》)由中国人民银行、中国银行保险监督管理委员会、中国证券监督管理委员会、国家外汇管理局以“银发〔2018〕106号”联合印发，这是规范金融机构资产管理业务的纲领性的政策法规，对各类金融机构均限定杠杆倍数、消除多层嵌套、“双十限制”等，并进一步明确要减少通道业务，旨在通过统一监管标准防止监管套利。在《资管新规》这一重要法规出台以后，传统的监管套利问题得到解决。在近年来宏观“去杠杆”的背景下，各类金融子行业面对同样的政策环境，其经营环境基本一致，业绩表现也不存在过去的“此消彼长”的状况，由公司基本面决定的股票价格变化也逐步趋同化,这在其十年间的公司节点网络结构的变化上得到很好的验证。

(二)检验

由于两个年度间上市公司数量的变化，网络节点数量也发生了变化，使用控制变量法，首先应该考虑节点的增加，再考察2009年度原有节点间的结构变动。

2019年比2009年新增了9家公司，将其去除后在阈值为0.5时考察网络结构变动的情况，结果如表3。

表3 去除新增节点后阈值=0.5时的复杂网络统计特性

由表3可知原有节点间的网络结构发生了很大变动，接下来用公司节点的介数来衡量其在网络中的重要性。节点的介数指复杂网络中所有最短的路径通过该节点的比例，介数越大，可以认为该节点在整个网络结构中越重要。

由表4、表5可知，不同公司在网络中的重要性发生了很大变动，有些公司的重要性提高，如sh600318，有些公司的重要性降低，如sz000563，同时也有节点的重要性未发生明显变化，如sh600817，其介数在2009和2019年度均为0，是典型的“边缘节点”。

表4 阈值=0.5时2009年度公司节点介数分布

表5 阈值=0.5时2019年度公司节点介数分布(去除新增点)

公司节点重要性的变动意味着在证券市场中，即使面对同样的监管环境，各家公司的经营状况也是处于不断变化的过程中，公司的业绩也会出现差异，其基本面的变化将会在其公司股票上得到体现，这也就意味着积极的投资者需要实时观察研究目标公司的经营状况，适时调整自己的投资组合，当资产组合中的节点公司股票关联程度过高时，需要更改配置比例乃至资产种类。若投资者的组合中持有大量该板块的“核心节点公司”，则建议不应再持有该板块的其他节点公司，即使一定要加大对该类公司的配置，也建议考虑持有“边缘节点公司”，以降低整个组合的系统性风险。

由表6可知，新增公司在2019年度的复杂网络中构成了几个重要节点，尤其是sh600643，其介数值是位于第二位的sz000415的近三倍。

表6 2019年度阈值=0.5公司节点介数分布

在删去节点sh600643后，网络结构变化如表7所示。

表7 去除节点sh600643后2019年度阈值=0.5时的复杂网络统计特性

图3 阈值=0.5时2020年度3月多元金融上市公司复杂网络拓扑结构

由表7易知复杂网络的图密度降低幅度较大，重要节点公司sh600643的消失减少了传播路径，但聚类系数未受到大幅影响，网络结构的小世界特性未遭破坏，节点公司sh600643没有对网络结构造成“大而不能倒”的影响。这意味着在同板块内部投资中，即使刻意回避了“核心节点公司”，包含较多同板块节点公司股票的资产组合也会有很大的系统性风险，研究结论进一步支持多元化分散投资。

那么外部宏观环境的剧烈变化，例如突发的股市崩盘是否会对板块的复杂网络拓扑结构造成严重影响,投资者又应如何应对这种冲击？2020年新冠疫情在全球的蔓延导致了资本市场的大幅震荡，美股在不到一个月的时间里4次触发熔断机制，资本全球化使得中国市场也无法独善其身，中国证券市场也发生了较大波动，下文对2020年3月这25家公司股票的相关性复杂网络拓扑结构进行研究，总计22个交易日。

从图3中可以发现，2020年3月多元金融类上市公司的复杂网络拓扑结构中，处于边缘的游离节点的个数较之2019年明显增多。这说明，在市场的剧烈波动时期，该网络公司股票之间的关联程度降低了。

由表8可以看出，受宏观冲击的2020年3月的复杂网络，在统计特性上其实更接近节点数目相对较少的2009年度的复杂网络。网络连通完整性显著降低，但依旧保留了小世界特性。接着通过介数分析2020年3月复杂网络中的节点属性。

表8 阈值=0.5时2020年3月多元金融类上市公司股票复杂网络统计

对比表9和表6，可以看出公司节点介数的变化，在表9中介数大于10的6个重要节点中，有两个重要公司节点是新加入的，在2019年度阈值为0.5的复杂网络中，公司sh600599的介数为0，而在2020年3月，其值达到了11.79。公司sh600139的2020年3月介数为30.06，在2019年度，它没有任何一条边达到阈值为0.5的统计标准。通过网络结构图，可以发现，这两个节点并非如公司sh600901一样，是典型的“中心节点”。典型“中心节点”相连节点多，且边的权重也偏大，统计特性上，sh600901和sz000563的节点度数均为18，而考虑到边的权重后，其加权度数分别为13.79和13.69。相较之下，节点度数同为18的sh600139的加权度数仅为12.72，而节点度数为14的sh600599，其加权度数仅为8.22，也是相同度数节点中最低的一个。其较高的介数应是由该节点和边缘节点的联系得来的，边缘节点度数小，相连边的权重也偏低，往往只和靠近中心的一两个节点相连，而这些靠近中心的节点则通过这种连接获得了一些“最短路径”，从而在介数统计中占有优势。为了验证，本文将介数为0～5的边缘节点去除后，再次构建2020年3月份的复杂网络拓扑结构。

表9 阈值=0.5时2020年3月份公司股票节点介数分布

与之前的复杂网络拓扑结构有所不同，图4中股票节点颜色模块化的依据不是节点的度数，而是节点的介数。结合表10和图4，可以发现，去除边缘节点后的2020年3月份的复杂网络是一个连接十分紧密的小世界网络，图密度达到了0.964，而在这个网络中，原先介数较高的sh600139和sh600599变成了所谓的“边缘节点”，去除了完整网络中边缘节点的情况下，它们在介数上的损失远超过那些完整网络中的典型“中心节点”，这印证了前文的推测，即它们是通过与边缘节点的连接在介数统计中占有优势。

表10 阈值=0.5时去除边缘节点后2020年3月份复杂网络统计特性

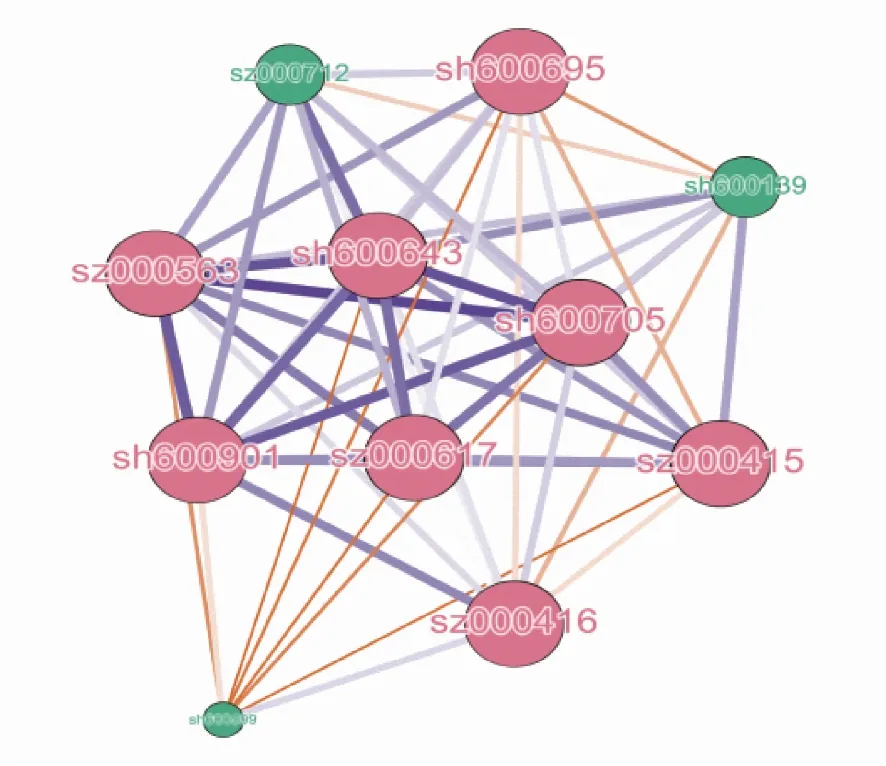
图4 阈值=0.5时去除边缘节点后2020年3月多元金融上市公司网络拓扑结构

以上研究表明，当市场遭到外部剧烈冲击时，“核心节点公司”和“边缘节点公司”的投资组合在风险分散上要优于“次级核心节点公司”和“边缘节点公司”的组合。巨大的冲击大幅降低了金融市场各组成公司间的关联性，尤其是板块中核心节点公司和边缘节点公司间的联系，在这种情况下，两者组合的系统性风险比在市场平静时的风险更低。而对于监管者来说，“次级核心节点公司”的这一性质可以使其成为相关监管部门监控系统性危机发展程度的重要观测对象。

对比2019年度和2020年3月份的复杂网络建模结果，我们可以发现sz000415、sz000416、sz000563、sh600901、sh600643、sh600705和sz000617这七个节点在这两个时期的复杂网络中都具有较高的度数与介数，它们对于整体网络的结构是否有重大影响，本文接下来进一步验证。去除以上七个核心节点后，对2019年度和2020年3月份的多元金融板块进行复杂网络建模。

对比表11和表2发现，去除核心节点后的2019年度复杂网络，图密度和平均聚类系数都有显著下降，而平均路径长度有所增加，核心节点的去除使得整个网络少了许多“捷径”，这一点反映在了表中统计特性的变化上。

表11 阈值=0.5时去除核心节点后2019年复杂网络统计特性

对比表12和表8，可以看出去除核心节点后对2020年3月份网络结构的影响与2019年度类似，且在程度上比2019年更为严重，在金融市场的动荡时期，联系紧密的核心节点对于整个网络的重要性提高了，综合来看，核心节点公司的移除会令网络更加分散化，联通程度更低。

表12 阈值=0.5时去除核心节点后2020年3月份复杂网络统计特性

综合上述，在证券市场处于平稳发展时期，投资者持有同一类型的多家公司股票，是较不理性的投资选择，尤其是仅持有该板块的“核心节点公司”。而当市场遭受较大外部冲击时，同板块内的投资组合的系统风险有所降低，“核心节点公司”和“边缘节点公司”的组合变得更有吸引力。对于证券市场的监管和稳定，“核心节点公司”是重中之重，而在危机时期，“次级核心节点公司”的监管也应被纳入重点范围，这就好比在城市爆发传染病时期守住出城的干道。

多元金融类上市公司股票的复杂网络拓扑结构，是否映射了现实经济生活中所代表公司之间的联系，我们对此进行探讨。一般而言，公司之间的联系主要有以下几种方式：一是企业之间由融资或者履约关系而产生的借贷或者担保关系，如牛晓健、崔璨的研究所揭示的河北担保圈问题[11]；二是企业之间交叉持股关系，几个企业互相持有对方的股权，从而在股东结构上产生一定的关联，如牛晓健、罗盛君等对中国证券市场240家国有上市公司的交叉持股复杂网络研究[12]。三是企业之间的生产经营上的供应链关系，例如上下游企业之间的商品或服务供销关系。通过查询Wind资讯和“企查查”等第三方工商登记查询的平台，我们未能获得多元金融类上市公司在这三个方面可能的详细关联的数据资料。

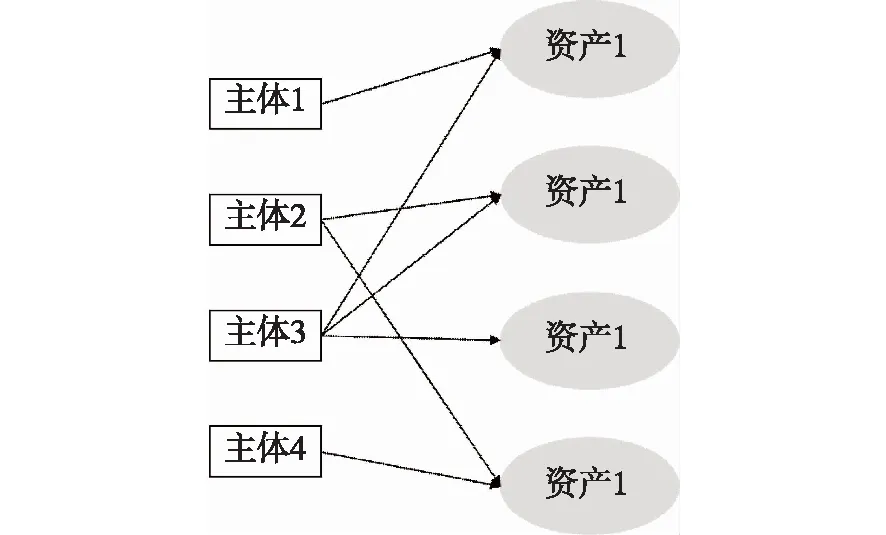
图5 基金-债券网络示意图

那么，多元金融类上市公司在复杂网络拓扑结构上的关系还有一种可能性，就是被类似的投资机构所共同持有，从而在价格的波动上呈现一定的相关关系，例如牛晓健、梁晓明运用复杂网络方法，通过构建基金-债券双层网络结构，探究了中国债券市场抵御风险冲击的能力，及其与市场参与者的行为和市场特征的关系[13]。研究发现，市场参与者所面临的杠杆率限制与收益率压力会交叉影响，形成正反馈机制，降低债市抵御风险的能力，而市场参与者的主动择时策略会影响上述能力。投资者面临的杠杆率限制越严格、收益率压力越大，市场流动性越差，债券市场抵御风险的能力越弱。完全分散化的投资者暴露于更多的风险来源中，反而降低了债券市场抵御风险的能力。但是由于数据的可得性有限，我们目前尚不能建立类似牛晓健、梁晓明的持有机构—股票的二分网络(图5)[13]，这也是本文今后进一步深化研究的一个方向。

五、结论与政策建议

本文通过对两个时期的多元金融板块复杂网络建模，研究了网络动态拓扑结构，对静态结构复杂网络研究做出了有益补充。由本文的研究可知，多元金融类上市公司内部的复杂网络拓扑结构呈现出较为明显的小世界特性，该网络拓扑结构在2009—2019年的时间跨度中有了很大的变化，除了新增上市股票的原因外，较为早期的股票间相关关系的变动也是一大因素。网络中上市公司股票间相关关系的变动，可能是因为《资管新规》等监管法律法规和宏观去杠杆等经济政策的影响，也可能是因为公司自身的经营状况的改变，使得其在行业中的相对重要性有了变化。在统一监管的政策框架下，从较长的时间跨度上看，网络拓扑结构总体向着节点联系越发紧密、平均路径长度更短的方向发展。板块内部资产组合的系统风险会随着节点关联性的提高而变得越来越大。

在剧烈的系统性危机的冲击下，证券市场板块内部的网络拓扑结构也会发生改变，总体来说，随着网络联通度的降低，边缘节点公司的增多，节点公司的重要性也会发生变动，一些本来无关紧要的节点公司会通过与边缘节点公司间的独特联系而跃升到次级核心节点的位置。因为在证券市场相对稳定的时期，图密度较大，网络联通程度更完整，边缘节点公司往往也会和一级核心节点公司有微弱的关联。此时，板块内部资产组合的系统风险有所降低，尤其是板块内“核心节点公司”和“边缘节点公司”的投资组合。

限于数据资料的可得性，我们尚未发现多元金融类上市公司股票复杂网络拓扑结构与其基本面在担保关系、借贷关系、供应链关系、股权关系等方面联系的依据，这也是本研究进一步深化的方向。

在股票板块的小世界复杂网络中，几个重要节点公司的所有连接往往呈现了大部分的网络信息，因此使得“指数成分股”的选择具有理论依据。而通过本文研究也能发现，一个网络中的节点公司重要性处于变动之中，“指数成分股”也应该及时更新，方能最好地反映市场的真实情况，有利于监管与投资。如果“指数成分股”长期不变，有可能造成资源的大量浪费和投资者的损失。企业发展是动态的，网络结构也是动态的，金融监管也应相应地变化。

在一个复杂网络中，节点公司的重要性有着较为明显的分级结构，重要的核心节点公司在网络中关联多并且联系密切，往往为网络提供了大部分的“捷径”，即使在网络遭到冲击的金融动荡时期，核心节点公司间的联系也较少受到破坏，资金和风险都会在这些链接迅速传播，这是金融市场监管的重点，在危机发生初期将波动控制在核心节点公司中有助于节省社会资源；次级节点公司在金融相对稳定时期没有突出的作用，但在动荡期却会变成核心节点公司和边缘节点公司间连接的纽带，对次级节点公司的监管有助于判断危机形势进而阻遏危机进一步发展，而边缘节点公司是整个网络中的最后一环，它们被波及意味着危机已经发展到全局性，此时精确地局部注入资金进行网络修复已不可能，必须在宏观上对整个网络进行重建，在这个过程中，股票节点公司的重要性排序有可能出现较大变动。对于投资者来说，过于集中于一个板块内部的资产组合会带来极大的系统风险，跨板块投资是消除风险的一个选择。而在整个市场都遭遇外部冲击的危机中，这种集中于板块内部的系统风险会有所降低，如果持有板块内部“核心股”的话，将“边缘股”加入投资组合会比加入“次级核心股”更能降低风险。