博彩性投机行为会影响流动性风险溢价吗？

张金清，李建宇

(复旦大学 金融研究院，上海 200433)

一、引言

在实证资产定价领域，如何解释因子组合的溢价一直是被关注的焦点问题。最传统的解释是风险补偿理论。近年来，一些学者提供了另一种解释思路，尝试从行为金融的角度去解释因子收益率溢价。例如，陆蓉和杨康发现，有限关注可以解释特质波动率溢价的成因[1]；朱红兵和张兵的研究结果表明，投资者的博彩行为可以解释MAX溢价的成因[2]。

风险补偿理论同样被用于解释流动性风险溢价的成因。然而，通过观测2015年股灾前后股票收益率的变动情况，本文发现投资者的博彩性投机行为也可能会影响A股市场上的流动性风险溢价。在2015年股灾前夕，股票市场空前繁荣，许多股票的收益率呈现出右厚尾、高偏度的特征。然而，在股灾爆发后，市场流动性急剧恶化，这些高偏度的股票遭受了严重的冲击。本文计算了在股灾爆发前两个月各个行业股票的平均偏度，结果显示，“信息运输、软件和信息技术服务业”公司的股票具有最高的偏度。图1展示了在股灾前后，这一行业股价指数的变动趋势。可以看出，在流动性危机爆发后，这一行业的的股票相较于市场平均水平出现了更大幅度的下跌。

在已有文献的研究中，股票收益率的偏度常常被用作刻画投资者的博彩性投机行为，博彩性投机指的是投资者购买彩票型股票的行为，Barberis和Huang结合前景理论，将彩票型股票定义为能够以很低的概率带来高额收益率的股票[3]。

图1 2015年股灾前后信息技术行业指数与A股市场指数变动趋势 注：图1选取了2015年4月15日至8月15日信息技术行业指数与A股市场指数的数据，为了比较两指数的变动趋势，本文选择以2015年4月15日为基期对数据进行调整。信息技术行业指数是所有按2016年证监会行业分类归属于“I”的股票的加权平均价格，A股市场指数是所有A股市场上股票的加权平均价格。另外，本文在图中标记了股灾爆发的时间点，以纵向虚线表示

由于高流动性风险的股票会在流动性恶化时发生更大程度的下跌，如果市场上具有很高的流动性风险溢价(即高流动性风险的股票具有更高的期望收益率)，那么在流动性恶化时，高流动性风险的股票会发生剧烈的波动。此外，由于博彩性投机行为在个体投资者中更加常见[2，4]，考虑到中国A股市场特殊的投资者结构，个体投资者的博彩性投机行为可能会对市场造成巨大的影响。因此，在中美贸易冲突和COVID-19疫情接连给市场流动性造成冲击的背景下，明确博彩性投机行为是否会增强流动性风险溢价，对降低流动性危机对市场的冲击有重要意义。

目前，关于流动性风险溢价的成因，已有文献主要提供了两种解释思路：一是将市场流动性作为状态价格变量引入跨期资本资产定价模型(ICAPM)，因而投资者会倾向于持有收益率变动方向与市场流动性变动方向相反的股票，以对冲市场流动性恶化的风险。在这一框架下，Pástor和Stambaugh、Lin等人分别证实了美国股票市场和债券市场上流动性风险溢价的存在性[5-6]。二是从偿付约束的角度解释溢价的成因，认为受到偿付约束的投资者为了避免在流动性恶化时陷入偿付危机，更倾向于持有低流动性风险的股票。Acharya和Pederson结合流动性调整的资本资产定价模型(La-CAPM)，阐释了偿付约束对流动性风险溢价的作用机制[7]。周芳和张维则以此为基础检验了中国A股市场上流动性风险溢价的存在性[8]。

总的来说，以上两种研究思路都仅从风险补偿的角度对流动性风险溢价的成因进行解释，认为流动性风险溢价是对投资者承担风险的补偿。在已有研究中，几乎没有文献讨论过博彩性投机等非理性行为对流动性风险溢价的影响，而现实情况表明，在市场流动性恶化时，进行博彩性投机的投资者可能会遭受更大程度的损失。这可能是由博彩性投机者购买“低价值”股票和进行短期投资的偏好所致。具体地来解释，一方面，彩票型股票是那些在过去出现过高额收益率的股票，这些股票的基本面特征往往难以匹配其较高的股价。在流动性恶化时，这些股票的股价更可能出现大幅下跌，给投资者带来损失；另一方面，个体投资者在进行博彩性投机时，会倾向于进行更加短期的投资[9]，那么，在流动性恶化时，这些投资者频繁变现股票的行为就会带来高额的交易成本。在这两方面因素的作用下，博彩型投资者更可能在流动性恶化时遭受更大程度的损失。因此，博彩型投资者可能会更偏好低流动性风险(即在流动性恶化时表现更好)的股票，并对高流动性风险的股票要求更高的收益率溢价。本文则从这一现实情况出发，分析博彩性投机行为对流动性风险溢价的影响。

本文选取2007年1月至2019年12月中国A股市场的股票数据，使用股票收益率的偏度和特质波动率作为衡量博彩性投机程度的代理变量。首先，根据双变量分组法和Fama-MacBeth回归方法，研究博彩性投机行为对流动性风险溢价的影响[10]。然后，通过Hou和Loh拆分方法，评估博彩性投机对流动性风险溢价的解释力度[11]。最后，通过分组的方式，分析博彩性投机行为对流动性风险溢价的影响机制。

相较于已有研究，本文可能的创新和贡献在于：第一，已有文献几乎没有讨论过博彩性投机等非理性行为对流动性风险溢价的影响，本文从这一角度进行分析，发现博彩性投机行为显著地增强流动性风险溢价；第二，本文利用Hou和Loh拆分方法，量化地评估博彩性投机对流动性风险溢价的解释力度，发现博彩性投机行为可以解释流动性风险溢价的54.95%，远高于其他传统定价变量的解释力度；第三，本文进一步分析博彩性投机行为对流动性风险溢价的影响机制，研究发现，投资者购买低价值股票的倾向和进行短期投资的倾向强化博彩性投机行为对流动性风险溢价的影响。

二、假设提出

(一)博彩性投机行为对流动性风险溢价的影响

在对中国市场流动性风险溢价的研究中，周芳和张维，王茵田和文志瑛分别在股票市场和债券市场上检验了溢价的存在性[8,12](1)本文也检验了中国A股市场流动性风险溢价的存在性。结果表明，基于流动性风险构造的多空组合可以实现年化17.45%的超额收益率，因篇幅原因，在正文中不再详细列出，读者可以登陆本杂志官网查看附录。。在引言中，关于流动性风险溢价的成因，本文回顾了已有文献提出的两种解释思路。第一种解释由Pástor和Stambaugh提出，他们认为市场流动性是一个重要的状态价格变量，因而投资者会倾向于持有收益率变动方向与市场流动性变动方向相反的股票，以对冲市场流动性恶化的风险[5]。第二种解释由Acharya和Pederson提出，他们从偿付约束的角度解释溢价的成因，认为受到偿付约束的投资者为了避免在流动性恶化时陷入偿付危机，更倾向于持有低流动性风险的股票[7]。

在已有研究中，绝大多数文献都从风险补偿的角度解释了流动性风险溢价的成因，然而，几乎没有学者对其他可能影响流动性风险溢价的因素进行分析。通过观测2015年股灾前后股票的偏度与收益率的关系，本文发现，在流动性恶化时，彩票型股票更可能发生更大程度的下跌。具体而言，这可能是由两方面因素导致的：一方面，彩票型股票的基本面价值可能无法匹配其股价，当市场流动性恶化时，这些股票可能会出现更大程度的下跌；另一方面，彩票型股票的投资者更可能进行短期投资，当流动性恶化时，这些投资者可能会承受高额的交易成本，加剧他们的损失。

基于这一现实情况，本文认为：进行博彩性投机的投资者会更加厌恶流动性风险，对高流动性风险的股票要求更高的溢价，进而，在博彩性投机的影响下，中国A股市场的流动性风险溢价显著地加强。由于更高的流动性风险溢价意味着流动性危机期间更剧烈的波动，因此，本文希望明确博彩性投机行为是否会增强A股市场的流动性风险溢价，故提出第一个假设。

假设H1：博彩性投机行为会显著地增强中国A股市场的流动性风险溢价。

为了对假设H1进行实证检验，本文借鉴已有文献的方法，以股票收益率的偏度和特质波动率作为衡量股票博彩特征的代理变量。偏度指的是股票收益率的三阶中心矩。Barberis和Huang提出，如果投资者具有与前景理论相一致的效用函数，即他们会偏好可能带来高额收益的小概率事件，那么他们会倾向于购买收益率偏度更高的彩票型股票，或者说高偏度的股票更容易引发投资者的博彩性投机行为[3]。特质波动率是股票的收益率序列对因子定价模型回归的残差标准差。Kumar认为，彩票型股票除了有更高的偏度之外，也有更高的特质波动率[13]。在此后的研究中，绝大多数文献都使用偏度和特质波动率作为衡量股票博彩特征的指标。Green和Hwang使用偏度作为博彩性投机的代理变量，分析了博彩性投机行为对IPO首日收益率的影响[9]。郑振龙和孙清泉使用偏度和特质波动率作为博彩性投机行为的代理变量，证实了中国A股市场存在明显的博彩性投机偏好，且博彩型股票具有更低的期望收益率[4]。Bali等人、朱红兵和张兵同时使用偏度和特质波动率作为代理变量进行实证检验，证实了博彩性投机行为是促成MAX异象的主要原因[2，14]。因此，对应于假设H1，本文使用偏度和特质波动率作为博彩性投机的代理变量，提出两个等价的假设。

假设H1a：股票收益率的偏度会影响流动性风险溢价：在偏度较低的股票组合中，不存在显著的流动性风险溢价；而在偏度较高的股票组合中，存在显著为正的流动性风险溢价。随着股票组合偏度的提高，流动性风险溢价也越来越显著。

假设H1b：股票的特质波动率会影响流动性风险溢价：在特质波动率较低的股票组合中，不存在显著的流动性风险溢价；而在特质波动率较高的股票组合中，存在显著为正的流动性风险溢价。随着股票组合特质波动率的提高，流动性风险溢价也越来越显著。

(二)博彩性投机影响流动性风险溢价的机制

假设H1意味着博彩性投机行为会显著地增强流动性风险溢价，进而加剧流动性恶化时市场的波动。因此，明确博彩性投机行为影响流动性风险溢价的具体机制，有助于提出更有针对性的政策建议。本文希望结合已有文献的研究结果，从彩票型股票自身的特征以及彩票型股票投资者的投资行为特点切入，研究博彩性投机行为影响流动性风险溢价的具体机制。

从彩票型股票自身的特征考虑，朱红兵和张兵指出，彩票型股票往往是“低价值”的股票，这些股票的基本面特征往往难以匹配其较高的股价[2]。在流动性恶化时，这些股票的股价更可能出现大幅下跌，给投资者带来损失。在进行实证检验时，朱红兵和张兵使用市净率指标来衡量股票是否是“低价值”的，他们的研究发现，在高市净率的股票组合中，MAX异象更显著[2]。借鉴这一思路，本文提出第二个假设。

假设H2：博彩性投机者具有购买低价值股票的倾向，这种倾向强化了博彩性投机行为对流动性风险溢价的影响。换言之，在市净率较高的股票组合中，博彩性投机行为对流动性风险溢价的影响更加显著。

从彩票型股票投资者的投资行为考虑，Green和Hwang指出，个体投资者在进行博彩性投机时，往往会进行更加短期的投资[9]。那么，在流动性恶化时，这些投资者频繁变现股票的行为就会带来高额的交易成本，放大他们的损失。本文使用换手率指标衡量投资者的短期投资偏好，并提出第三个假设。

假设H3：博彩性投机者具有进行短期投资的倾向，这种倾向强化了博彩性投机行为对流动性风险溢价的影响。换言之，在换手率较高的股票组合中，博彩性投机行为对流动性风险溢价的影响更加显著。

三、流动性风险指标构造与变量选取

(一)数据来源

本文的股票收益率、公司市值、会计指标、无风险收益率等数据均来自于CSMAR数据库。本文选取的股票样本为全部A股股票，剔除ST、PT股票数据后，最终剩余2944只股票。因子收益率根据流通市值加权。本文的数据均经过了1%的Winsorize缩尾处理，以避免极端值的影响。本文选取的数据样本区间为2007年1月至2019年12月，样本区间从2007年开始是因为股权分置改革对中国A股市场的流动性影响很大，不利于流动性风险指标的估计，直至2006年底股权分置改革全面完成。

(二)流动性风险指标构造

本文借鉴Pástor和Stambaugh以及Lin等人的思路构造个股的流动性风险测度指标[5-6]。张峥等人的实证结果表明，在中国股票市场上，Amihud指标要优于其他低频的流动性代理指标[15-16]。因此，本文使用Amihud非流动性代理指标构造流动性风险。具体而言，第i支股票在第τ个交易日的Amihud指标由式(1)给出。

(1)

其中，ri,τ为第i支股票在第τ个交易日的收益率，volumni,τ为第i支股票在第τ个交易日的交易金额(千万元)。将个股的非流动性按流通市值加权平均得到市场非流动性水平。

(2)

借鉴Pástor和Stambaugh以及Lin等人构造市场流动性新息(或扰动)的方法[5-6]，结合样本数据，本文选择如下时间序列方程来拟合市场流动性序列。

(3)

其中，ΔILLIQM,τ=(Mτ/M1)(ILLIQM,τ-ILLIQM,τ-1)，eτ为扰动项。

(4)

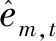
图2 市场流动性信息变动趋势注：图2的数据区间为2007年1月至2019年12月，图中两处阴影部分分别代表2008年金融危机以及2015年股灾

(三)变量选取

除了按照上述方法构造的流动性风险测度指标(Beta)外，本文选取的变量还包括：(1)传统定价指标，包括市值(Size，千万元)、账面市值比(BM)、Amihud指标(Amihud)和换手率(Turnover)，(2)股票博彩特征指标，包括股票的收益率偏度(Skew)。

股票i在第m个月的偏度按如下方法计算：

(5)

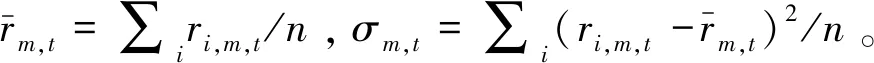
(6)

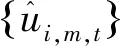
表1的子表1报告了在样本区间内所有样本股票的统计特征，其中Return为月度收益率，Size的单位为千万元(2)本文在表1中报告的指标都未经过处理，在应用这些指标进行实证分析时，本文对这些变量都进行了1%的Winsorize缩尾处理。。表1的子表2报告了各个变量之间的Pearson相关系数。子表2的结果表明本文选取的两个股票博彩特征指标(Skew和IVOL)之间具有一定的相关关系(19.40%)，即两个指标刻画了共同的股票特征，与Kumar的发现一致[13]。市值与偏度(特质波动率)呈负相关，说明博彩行为更可能发生在小市值的股票中。流动性风险指标与Amihud指标的相关性不高(相关系数为0.41%)，说明股票的流动性和流动性风险刻画了股票不同的性质。

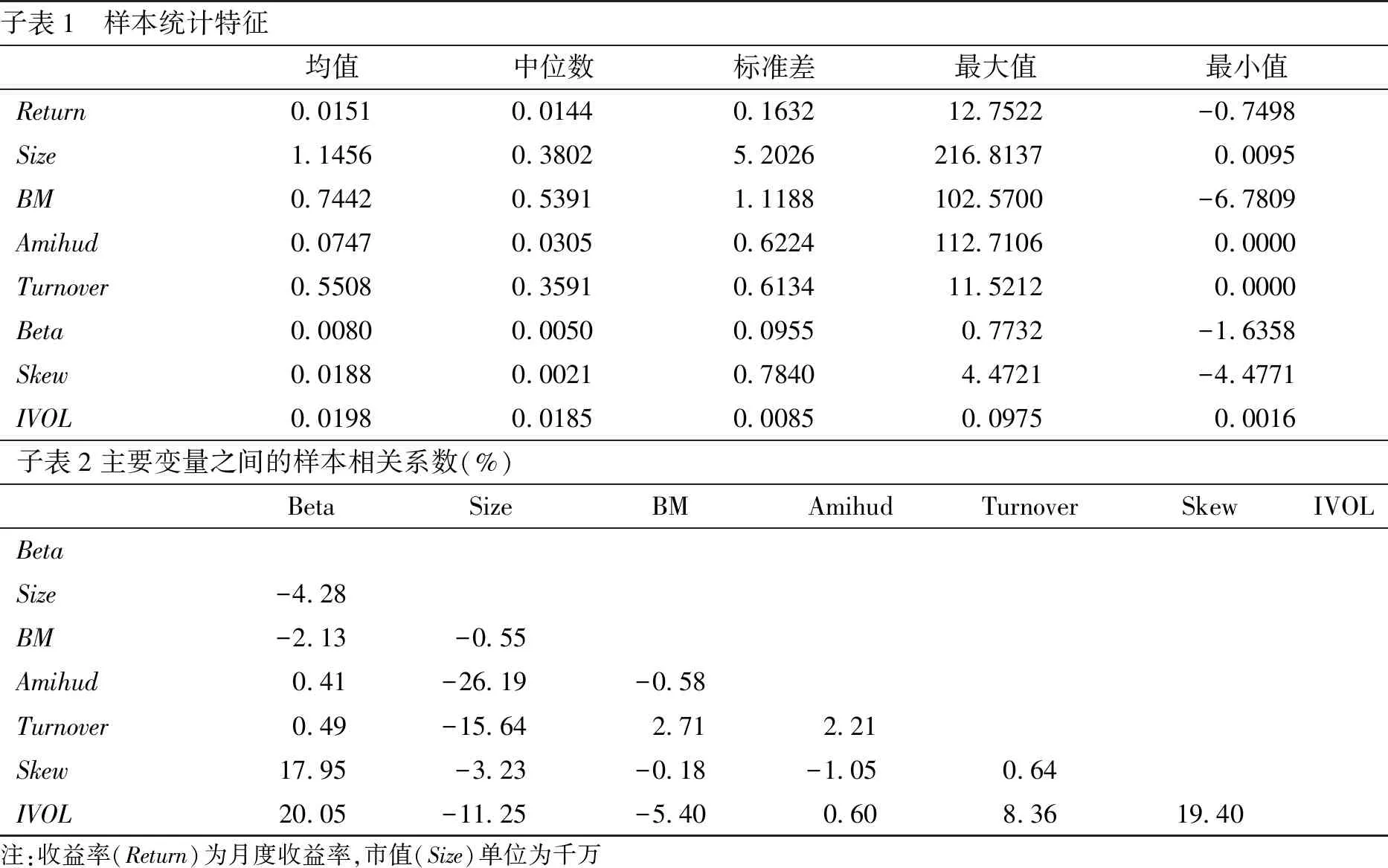
表1 变量的描述性统计

四、博彩性投机行为与流动性风险溢价

在这一部分中，本文希望对第二部分提出的假设H1进行实证检验。利用双变量分组和Fama-MacBeth回归两种方法，探究博彩性投机行为是否增强了中国A股市场上的流动性风险溢价。而后，为了更加量化地评估博彩性投机行为对流动性风险溢价的影响程度，本文通过Hou和Loh拆分方法，评估以偏度和特质波动率衡量的博彩性投机行为对流动性风险溢价的解释力度[11]。

(一)双变量分组分析

本文希望根据双变量分组方法，检验股票组合的流动性风险溢价是否会随着博彩特征的增强而更加显著。双变量分组分析方法先后根据两个变量(下称第一分组变量和第二分组变量)将全部股票分为5*5个股票组合，进而检验当第一分组变量变化时，基于第二分组变量构造的因子组合的超额收益率变动情况。具体而言，在每个月末，先基于股票的偏度(或特质波动率)将股票等分为五组，再按流动性贝塔的大小对每个组合进行第二次五等分，共形成25个投资组合，并在每个偏度(或特质波动率)分组下构造流动性风险的多空组合，每个组合内的股票按照流通市值加权构造资产组合。最后，将构造的25个资产组合和5个多空组合的收益率序列对三因子模型回归，计算超额收益率。

表2展示了基于偏度-流动性风险进行双变量分组的实证结果。结果显示：流动性风险溢价的大小和显著性水平随股票组合偏度的提高而上升，经三因子调整后的超额收益率从0.2114%递增至1.5146%。在偏度最低，即博彩特征最弱的股票组合中，流动性风险溢价并不显著；而在其余四个博彩特征较强的股票组合中，流动性风险溢价均表现显著。表2的结果验证了假设H1a：在收益率偏度较低的股票组合中，不存在显著的流动性风险溢价，而在偏度较高的股票组合中，存在显著为正的流动性风险溢价。随着股票组合偏度的提高，流动性风险溢价也越来越显著。

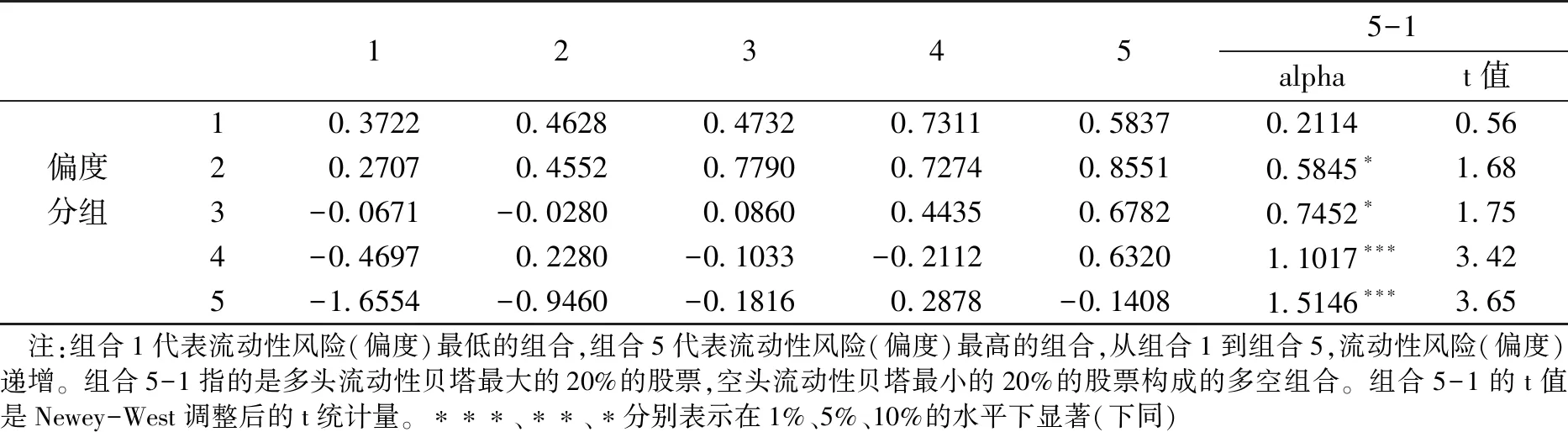
表2 基于偏度-流动性风险双变量分组分析的超额收益率

从第二个股票博彩特征特质波动率出发，本文对假设H1b进行了检验。表3的结果表明，流动性风险溢价的大小和显著性随股票组合特质波动率的上升而增加，经三因子调整的超额收益率从0.2702%单调递增至2.0859%。在特质波动率最小，即博彩特征最弱的股票组合中，流动性风险溢价并不显著；而在其余四个博彩特征较强的股票组合中，流动性风险溢价均表现显著。因此，表3的结果验证了假设H1b。

表3 基于特质波动率-流动性风险双变量分组分析的超额收益率

(二)Fama-MacBeth回归

双变量分组的结果表明，在中国A股市场上，博彩性投机行为会影响流动性风险溢价.但是，这种影响可能是由流动性风险与其他变量的相关性导致的。因此，本文利用Fama-MacBeth回归分析方法，检验在控制其他传统定价变量后，博彩性投机行为对流动性风险溢价的影响是否依然稳健存在。

Fama-MacBeth方法由Fama和MacBeth提出，该方法提供了一种在控制其他定价变量后检验核心解释变量与股票期望收益率之间关系的思路[10]。具体来说，在每个月末，使用所有符合要求的样本股票拟合如下回归，得到各斜率系数的时间序列。

Returni,t=β0+β1Betai,t-1+β2Betai,t-1·Skewi,t-1+x′i,t-1γ+εi,t

(7)

Returni,t=β0+β1Betai,t-1+β2Betai,t-1·IVOLi,t-1+x′i,t-1γ+εi,t

(8)

其中，Skew和IVOL分别为偏度和特质波动率，xi,t-1为一组控制变量，包括市场风险系数、市值、账面市值比、非流动性和偏度(特质波动率)。而后，取斜率系数序列的均值作为Fama-MacBeth回归的结果。在这一部分中，本文关注的重点是Fama-MacBeth回归中流动性贝塔与偏度(或特质波动率)交叉项前的回归系数β2，β2显著为正则意味着流动性风险溢价会随着股票博彩特征的增强而增强。

Fama-MacBeth回归的结果展示在表4中。Skew和IVOL以及各控制变量前的斜率系数的方向均与已有金融理论相一致。除账面市值比外，其他的定价变量均具有显著的定价效力，这与Liu等人的实证结果一致[17]。模型1表明，在控制传统定价变量后，高流动性风险的股票会有更高的期望收益率，即中国A股市场上存在显著的流动性风险溢价(3)本文在附录A中更加细致地检验了流动性风险溢价的存在性。。本文重点关注流动性风险溢价与股票博彩特征之间的关系：在模型2、3、4、5中，Beta前的系数不再显著为正，说明当不存在明显的博彩性投机行为时(即控制Skew和IVOL较低时)，不存在显著为正的流动性风险溢价；交叉项前的系数显著为正，说明流动性风险溢价随博彩特征的增强而显著增大，与前文双变量分组的结果保持一致。因此，Fama-MacBeth回归的结果表明，在对传统定价变量进行有效控制的前提下，假设H1a和H1b依然成立。

表4 Fama-MacBeth回归结果

(三)Hou和Loh拆分方法

在上文中，本文通过双变量分组和Fama-MacBeth回归方法，证实了博彩性投机行为会增强流动性风险溢价。在此基础上，本文希望评估博彩性投机行为对流动性风险溢价的解释力度。Hou和Loh提出了一种拆分方法，用来评估各种潜在解释变量对因子收益率溢价的解释能力[11]。Hou和Loh利用这一方法估计了各种潜在解释变量对特质波动率溢价的解释能力，并指出这种方法可以用于解释其他因子收益率溢价[11]。陆蓉和杨康使用这一拆分方法，在中国A股市场上评估了一些变量对特质波动率的解释力[1]。因此，本文也将沿用这一思路，计算博彩性投机对流动性风险溢价的解释力。

Hou和Loh拆分方法本质上是在Fama-MacBeth回归的基础上，将因子收益率溢价拆分为可以由潜在解释变量解释的部分和无法由潜在解释变量解释的部分。具体而言，Hou和Loh拆分方法可以分为三个步骤。

第一步与Fama-MacBeth回归相似，在第t个月末，用股票收益率对前一个月的流动性风险进行回归。

Returni,t=αt+γtBetai,t-1+εi,t

(9)

第二步，用股票的流动性风险对潜在的解释变量Candidate回归。

Betai,t-1=at-1+δt-1Candidatei,t-1+μi,t-1

(10)

第三步，将第一步得到的回归系数γt拆分成可以由潜在解释变量Candidate解释的部分和无法由潜在解释变量解释的部分。

(11)

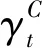
根据这一方法，本文评估了偏度和特质波动率对流动性风险溢价的解释力度，实证结果展示在表5中，其中模型3同时将偏度和特质波动率作为潜在解释变量。在表5的步骤1中，Beta前的系数显著为正，说明中国A股市场存在显著的流动性风险溢价效应。步骤3中的拆分结果表明，偏度和特质波动率可以分别解释流动性风险溢价的28.19%和36.40%，同时将偏度和特质波动率作为潜在解释变量时，可以解释流动性风险溢价的54.95%，这一结果在统计意义上非常显著。

此外，本文还分析了传统定价变量(市值、账面市值比和Amihud指标)对流动性风险的解释力度，以便与表5的结果形成对照。对这三个变量的Hou和Loh拆分结果展示在表6中。结果表明，市值、账面市值比、Amihud指标对流动性风险溢价的解释力度分别为4.23%、5.09%、2.31%，明显低于偏度和特质波动率对流动性风险溢价的解释力度。因此，根据Hou和Loh拆分结果，博彩性投机行为对流动性风险溢价的解释力在经济意义和统计意义上都非常显著。

表5 对偏度和特质波动率的Hou and Loh拆分结果

表6 对市值、账面市值比、流动性的Hou和Loh拆分结果

五、博彩性投机行为对流动性风险溢价的影响机制

鉴于博彩性投机行为会对流动性风险溢价造成如此显著的影响，本文希望进一步研究博彩性投机行为影响流动性风险溢价的具体机制，以便为降低流动性危机对市场的冲击提出更加有效的建议。

在第二部分中，本文结合已有研究，对博彩性投机行为影响流动性风险溢价的机制进行了分析。从彩票型股票自身的特征来看，彩票型股票的基本面可能无法匹配其较高的股价，从进行博彩性投机行为的投资者来看，这些投资者可能具有更加短期的投资倾向。因此，在流动性恶化时，彩票型股票更可能出现更大程度的损失。换言之，投资者购买低价值股票的倾向和进行短期投资的倾向强化了博彩性投机行为对流动性风险溢价的影响。在这一部分中，本文希望通过分组的方式，对假设H2和H3进行验证。

为了对假设H2进行实证检验，本文在每个月末，根据股票的市净率构造投资组合，进而观测是否在高市净率(即低价值)的股票组合中，博彩性投机行为能够更显著地增强流动性风险溢价。具体而言，在每个月的月末，按照股票的市净率由高到低将全部样本股票等分为十组。而后，在每个组合中拟合回归式(7)和回归式(8)，得到每个组合中回归系数的时间序列，并按Fama-MacBeth回归的思路求取均值。如果在市净率较高(即价值较低)的股票组合中，博彩性投机行为能够更显著地增强流动性风险溢价，那么假设H2得以验证，投资者购买低价值股票的倾向会强化博彩性投机行为对流动性风险溢价的影响。相应的分组结果展示在表7中。

在表7中，从组合1到组合10，组合的市净率依次增加，本文重点关注在低价值的股票组合中，博彩性投机行为对流动性风险溢价的影响程度(即表7的后几行交叉项的显著性水平)。结果表明，博彩性投机对流动性风险溢价的影响存在异质性效应，在高市净率的组合中，博彩性投机对流动性风险溢价的影响(即交叉项前的系数)显著为正，而当市净率较低时，博彩性投机行为对流动性风险溢价的影响并不显著。表7的结果验证了假设H2，博彩性投机者具有购买低价值股票的倾向，这种倾向强化了博彩性投机行为对流动性风险溢价的影响。

为了对假设H3进行检验，本文按照相同的思路，在每个月末根据股票的换手率进行分组，检验在高换手率的股票组合中，博彩性投机行为对流动性风险溢价的影响是否会更加显著。分组的结果展示在表8中。表8的结果表明，在不同的换手率分组下，博彩性投机对流动性风险溢价的影响存在异质性效应，在高换手率的组合中，博彩性投机对流动性风险溢价的影响显著为正，而当换手率较低时，博彩性投机行为对流动性风险溢价的影响并不显著。表8的结果验证了假设H3，投资者进行短期投资的倾向加强了博彩性投机行为对流动性风险溢价的影响。

表7 不同市净率分组下博彩性投机行为对流动性风险溢价的影响程度

表8 不同换手率分组下博彩性投机行为对流动性风险溢价的影响程度

六、结论

本文基于对2015年股灾前后股票的偏度和收益率之间关系的观测，研究了博彩性投机行为对流动性风险溢价的影响。本文选取2007年1月至2019年12月中国A股市场的股票数据，使用股票收益率的偏度和特质波动率作为衡量博彩性投机程度的代理变量，首先，根据双变量分组法和Fama-MacBeth回归方法，研究了博彩性投机行为对流动性风险溢价的影响，然后，通过Hou和Loh拆分方法，评估了博彩性投机对流动性风险溢价的解释力度，最后，通过分组的方式，分析了博彩性投机行为对流动性风险溢价的影响机制。本文的结果表明：第一，博彩性投机行为显著地增强了流动性风险溢价，在博彩特征较强的股票组合中，存在显著的流动性风险溢价，而在博彩特征不明显的股票组合中，流动性风险溢价并不显著，随着股票博彩特征的增强，流动性风险溢价的大小和显著性递增。第二，根据Hou和Loh拆分的结果，博彩性投机可以解释流动性风险溢价的54.95%，远高于其他传统定价变量对流动性风险溢价的解释力度。第三，博彩性投机者具有购买低价值股票的倾向和进行短期投资的倾向，这两种倾向强化了博彩性投机行为对流动性风险溢价的影响。

鉴于博彩性投机对流动性风险溢价造成的重大影响，本文提出如下建议：要引导投资者树立价值投资观念，正确认识彩票型股票，抑制投资者的短期投机倾向；通过加大机构投资者在市场中的参与程度，降低个体投资者的博彩性投机行为对市场的冲击。通过这些举措，减弱博彩性投机行为对流动性风险溢价的影响，以降低流动性恶化时的市场波动。