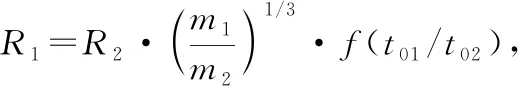基于量纲分析的燃料云雾半径计算

2021-06-02徐启明解立峰王永旭凤文桢宋先钊

兵器装备工程学报 2021年5期

徐启明，解立峰，王永旭，凤文桢，宋先钊，李斌

(1.南京理工大学化工学院，南京 210094； 2.中国兵器科学院宁波分院，浙江宁波 315103)

燃料抛撒形成云雾现象的研究在军事和工业上都有着重要的关注度。其在军事上一直是燃料空气炸药的(Fuel Air Explosive， FAE)重要研究方向，在工业上也可为预防可爆燃料云雾的形成和计算安全距离提供参考，同时相关研究成果可应用于消防灭火弹[1-2]。

目前对于燃料云雾抛撒规律的研究以实验为主，方伟等[3]利用高速摄影观测不同密度燃料抛撒过程，发现燃料密度的增加有利于燃料云雾的发展。郭学永等[4]系统研究了各种参数，如长径比、比药量和壳体材料等对于云雾膨胀半径的影响，给出了这些参数对于膨胀半径的影响规律，但是没有根据这些参数推出理论模型。Zabelka[5]根据中心药爆炸后驱动力和气动阻力的地位变化，将云雾扩散分两个阶段：近场阶段和远场阶段。其中近场阶段驱动力主导，燃料做加速运动，远场阶段阻力主导，燃料做减速运动。张奇等人[6]通过对加速阶段和减速阶段分开进行分析，代入一些相关参数证明了燃料分散最终半径符合相似定律。

上述研究分析了各类参数对于燃料云雾半径的影响，但并未给出一般性公式，每次改变装药质量都需要重新进行实验，而大装药质量的燃料抛撒实验由于成本高昂且实验复杂而难以进行，陈嘉琛[7]为了研究云雾场分布的尺度效应，在2 kg云爆装置实验的基础上，以模拟替代了7 kg、13 kg和100 kg云爆装置的实验研究。而且燃料云雾抛撒实验过程复杂，影响因素多，导致可用的数据和规律较少，陈明生[8]对大体积扇形装药结构燃料抛撒问题进行了系统研究，但是对于相似装药结构下其他装药质量的燃料云雾半径还没有足够数据进行表征。抛撒过程的研究涉及爆炸力学、流体力学、计算力学、动态测试技术等多个复杂学科[9-10]，目前所给出的模型大多为经验公式，不适用于普适实验。

量纲分析作为一种研究手段，不仅可以快速地找出问题一般性规律，暴露出主导控制参量，还可以在分析时简化研究，建立起左右两端量纲相同的模型[11-13]。本文通过量纲分析的手段，推导相似弹体结构及装药条件下云雾抛撒半径的变化模型，并通过实验验证了该模型的适用性。

1 相关参数的推导

本文中涉及参数及其符号见表1。

云雾抛撒过程可分为3个阶段，分别是加速运动阶段、减速运动阶段和湍流运动阶段[14]。其中加速阶段会在几毫秒内结束，由于目前设备和实验条件的限制，对加速阶段难以准确细致的观测到。通过实验数据能发现，抛撒云团到后期一般呈现为扁平圆柱形[15-16]，以中间弹体为对称轴对称。在本文中将其视为二维平面情况进行分析计算，忽略重力加速度的影响。

表1 文中涉及参数

将每毫秒云雾抛撒半径变化不超过0.1%视为达到终点，取达到这个状态时所需时间为t0。对于从0到t0时刻的云雾半径变化，从已有的抛撒实验可以看出，不同质量燃料云雾半径变化过程是相似的，都是由陡峭转向缓慢的变化，且t0是随着装药质量的增加而非线性增加的，故认为将t/t0相同时的云雾半径进行对比分析更为合理。选取两组实验参数及实验条件基本相同的数据，分别是300 kg液固燃料的抛撒和80 kg液固燃料的抛撒，通过高速摄像机读取燃料云雾半径变化如图1所示，将数据对时间进行求导，得到燃料抛撒时的速度变化，然后以t/t0为横坐标，u纵坐标进行作图(见图2)，从图2可以看出，从初始点开始，抛撒基本就处在减速阶段[17]，且加速度的绝对值一直在减小，直至终点时趋向于0。观察速度变化图形，考虑到中心装药、燃料量及读取数据时的误差等，分析认为t/t0可以作为一个相似数。

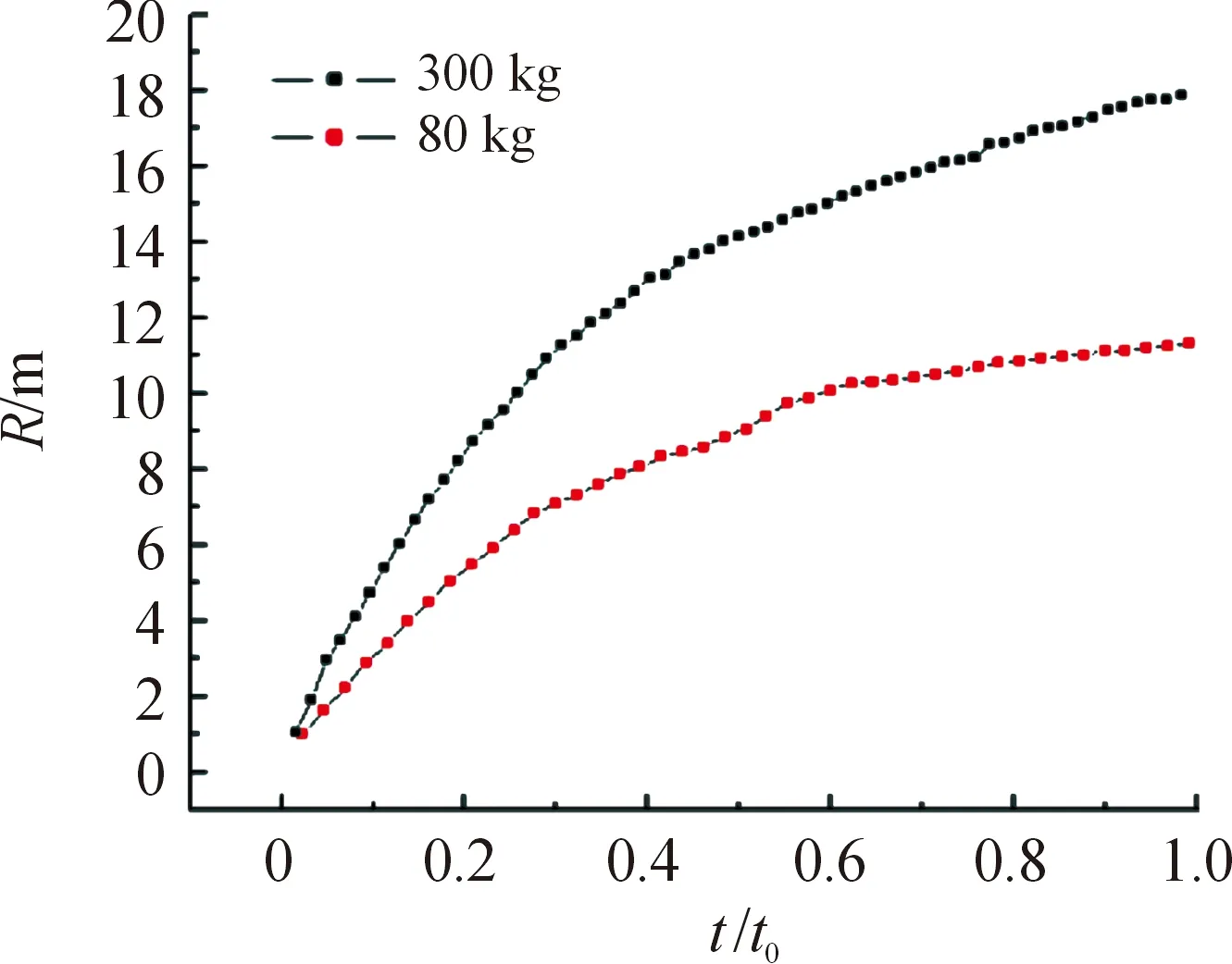
图1 300 kg和80 kg燃料云雾半径曲线

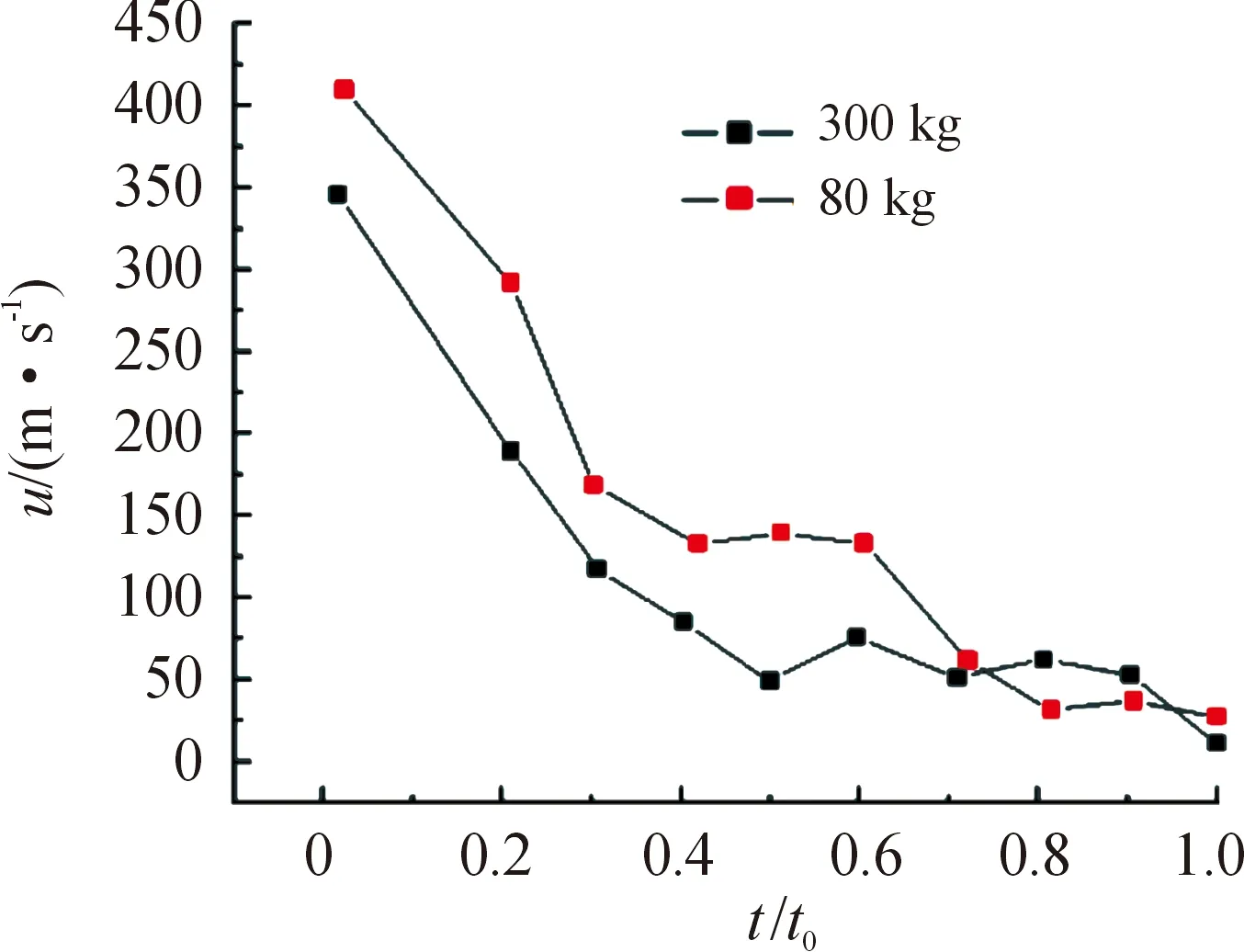
图2 300 kg和80 kg燃料云雾u的关系曲线

2 量纲分析及方程推导

量纲是物理量的种类属性，目前学术界给出的相似数基本都是无量纲数，如Laplace数和Taylor数等，本文使用的理论基础定理是量纲分析的一个重要定理，此定理的基本定义有以下3个[18]，分别是：

基本定义1:目前公认的量纲一共只有7个，所有其他的物理量都是这几个基本量的导出量；

基本定义2:量纲一致性定律，只有量纲保持一致的物理量才能在公式中进行相加减；

基本定义3:任何物理量写成量纲式一定是几个基本量纲的幂次乘积形式。

在相似装药结构下对云雾尺寸进行分析，认为影响因素有r0、m、M、t/t0、ρ、u0、F、E，本次将模型近似为在平面情况下进行思考[19]，故不考虑当地重力加速度g。且对于云雾变化缓慢一段不再代入分析，故不考虑雷诺数Re。基于Gurney方程，假定爆炸是瞬态的，中心装药爆炸的总能量完全转化为燃料颗粒和爆炸产物的动能[20]。

于是有R=f(r0、m、M、t、ρ、u0、F、E、t/t0)，涉及的基本量纲有3个，分别是[L]、[M]和[T]。将本次分析涉及的量纲列表，如表2所示。

表2 分析中涉及的量纲

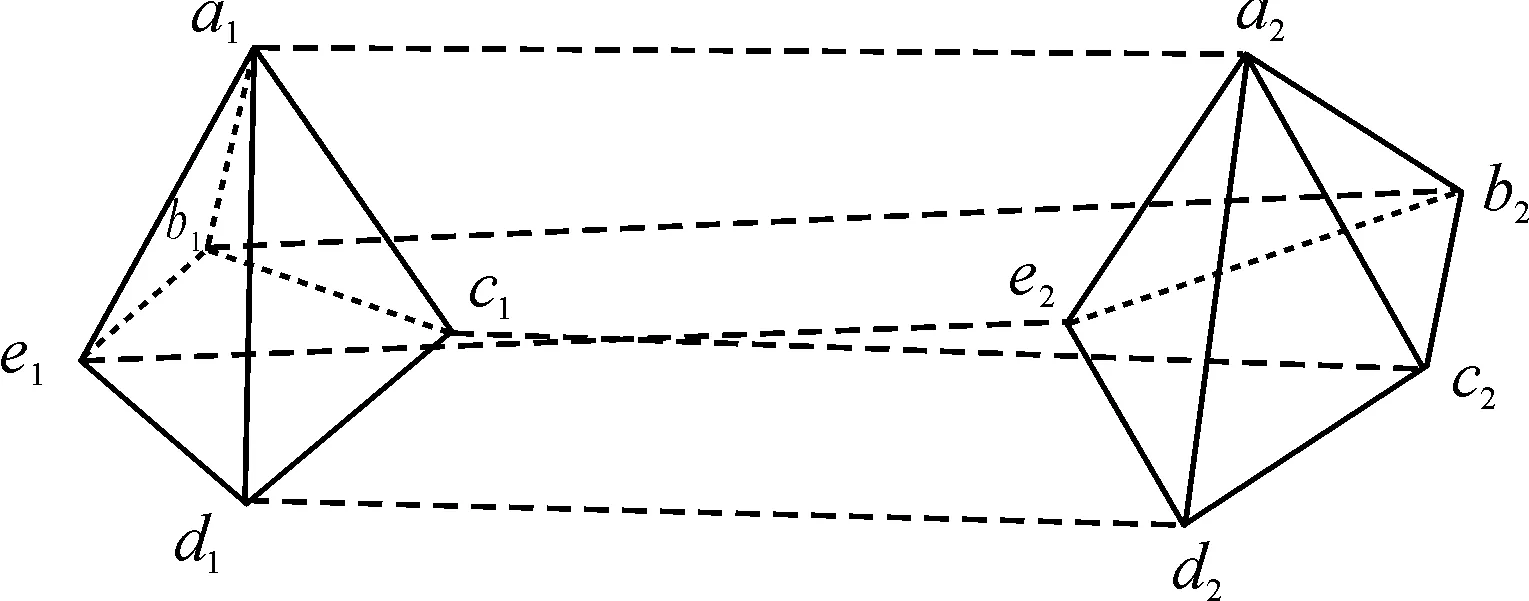
取任意量燃料为一燃料单元，抛撒过程中单元中燃料颗粒由于速度差异会不断变形，但是其总体质量不会发生变化，符合拉格朗日条件下的质量守恒，抛撒过程中任一云雾单元会出现如图3所示的变化。

根据拉格朗日情况下的质量守恒，我们假定在实时构型下所选定的单元密度为ρ，体积为dv，则在运动过程中有ρ0·dV=ρ·dv，u=dR/dt，其中ρ0和dV为单元初始密度和体积[21]，有：

ρ=ρ0(1-div·u)

(1)

即有：ρ=Ψ(R)。

ρ0, dV, u0 ⟹ ρ, dv, u

认为中心装药爆炸后，能量全部用于燃料加速，对于某一单元有：

(2)

可知F=Φ(E，u0，t)，联系上述分析认为参量F、u0、ρ是可以由其他参量表示的导出量，故进行无量纲分析时这几个参量可以舍去[22-24]。

取r0、m、t为基本量纲，则其他物理量有如下表示：

根据量纲齐次原则，可以得到：

1+a1=0，b1=0，c1=0；a2=0，1+b2=0，c2=0；2+a3=0，1+b3=0，-2+c3=0；a4=0，b4=0，c4=0。

(3)

在确定了装药条件后，式(3)中r0、u0、E、m可以视为常数，此时对于相似装药结构有，

(4)

对于2种参数基本相同的确认弹体，有，

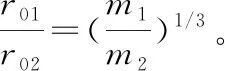
可对式(4)进行化简如下：

(5)

因此，对于相似装药结构的燃料云雾半径比，便转化为质量比的立方根和时间比的关系式，对于其中的时间比，目前没有准确的理论公式进行表征，在本文中通过实验室已有数据确定一个经验公式。不同质量燃料t0的有关参数如表3所示。

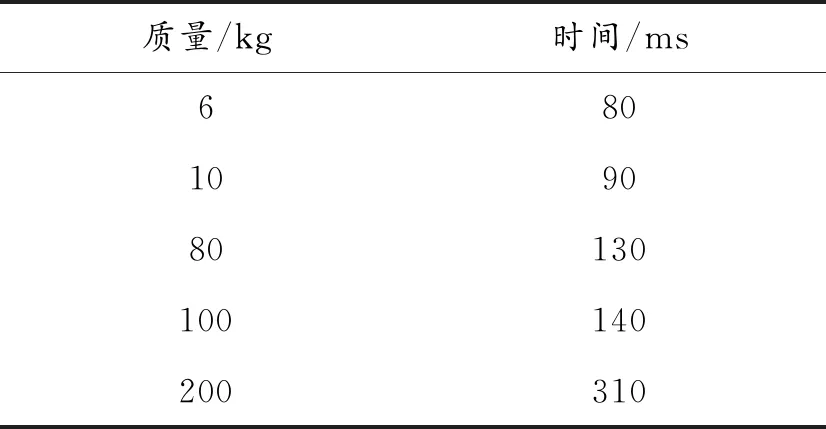
表3 不同质量燃料t0的有关参数

经验公式为t01/t02=e0.004 206·(m1-m2)，其准确度为0.99。

3 实验及分析

实验选取3组燃料量数据，分别为300 kg、80 kg和10 kg，其中300 kg和80 kg为作为算例，10 kg是实验。保证实验条件类似，3组实验装填燃料都是含铝液固燃料，壳体均采用铝质材料，且上端板厚度大于侧板，中心装药为TNT压装药柱，3种弹体具有相同的长径比和比药量。

其中10 kg装置如图4所示，弹体由中心管、侧部弹体、上下加厚端板组成，由雷管引爆传爆药柱在上端来激发TNT，其中弹体总重15 kg，侧面采用0.3 cm铝板制成，上下端板为1.5 cm的加厚铝板。燃料量为10 kg，比药量为1%，弹体高为40 cm，底部半径为10 cm，为防止燃料膨胀，弹体有一定留空，本次试验炸高为1.5 m。

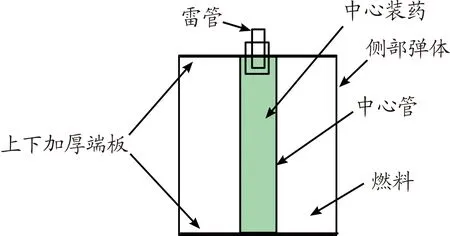
图4 试验战斗部示意图

对于本次实验，取2 ms、10 ms、90 ms时刻的高速摄像机拍摄照片如图5所示。

由图5可以看见，2 ms时，刚刚起爆，各个部分没有速度差异，呈现的云雾类似于圆柱形，能够看见有白色的尖峰出现[25]。10 ms，云团经过一段时间的发展，出现扁平状。90 ms时，云雾边缘发散，出现明显湍流运动，此时云雾分散速度及加速度已经趋向于0[26]，形状类似帽子形。

图5 10 kg抛撒照片

10 kg试验及其计算值如图6所示，云雾半径在t/t0=0.3前随时间变化较快，t/t0=0.3时变化减慢，这一阶段驱动力小于气动阻力，随后液体云雾发生了剥离破碎及挥发，进入湍流运动阶段并扩散[27]。

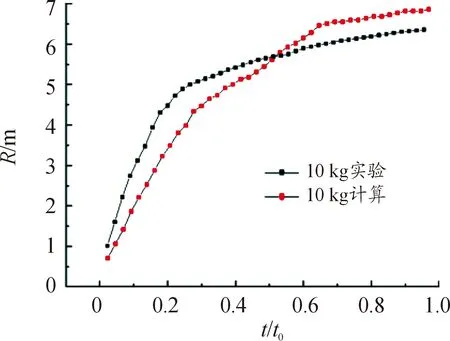
图6 10 kg试验及其计算值曲线

利用300 kg和80 kg的数据中云雾抛撒时间及其相对应的抛撒半径，选取相应5个点(见表4)代入推导公式中进行高斯拟合。

表4 拟合所用数据

得到最终公式为：

[3.458×(sin(e0.004 206×(m1-m2)-3.14))+0.043 77×((e0.004 206×(m1-m2)-10)2)+0.966 2]

(6)

通过拟合出来的公式，我们基于80 kg的数据进行10 kg燃料云雾半径计算，结果如图6所示。

图6中10 kg计算值是基于80 kg算例用公式计算得到，故其曲线与图1中80 kg算例相似，在t/t0=0.5附近有异常上升，认为符合情况。从图6可以看出，2条曲线在t/t0=0.55附近有重合，在0.55前取3个点，0.55附近取一个点，0.55后取3个点，求得平均相对偏差为12.8%，在接近抛撒终点时相差7.9%。可以认为推导的燃料云雾抛撒半径公式符合云雾抛撒的一般规律及趋势，且一致性较好。