基于进化BP神经网络的磨削温度预测研究∗

孙为钊 周 俊

（上海工程技术大学机械与汽车工程学院 上海 201620）

1 引言

磨削加工是现代机械制造中的一种重要工艺技术。由磨削加工可以得到比较满意的尺寸精度、形状精度、表面质量等。由于磨削加工的时间较短以及加工的金属层较薄，在磨削加工过程中产生的热量很大一部分会集中在磨削区内，在工件表面形成局部高温。特别是当温度在超过某一临界值，就会引起表面热损伤，从而降低零件的使用性能和可靠性。因此，研究磨削温度场分布对控制磨削温度具有重要意义。

国内对磨削温度的预测有了一定的研究。马占龙［1］、宋慧东［2］等利用BP算法对磨削温度进行了预测，所得结果与实验结果比较接近。蒋天一［3］等利用改进型BP神经网络对球面磨削的最高温度进行了预测，所得结果较传统的单一BP神经网络有了较大提升。马生彪［4］利用RBF和BP神经网络分别对磨削温度进行了预测并进行了比较，结果表明，RBF神经网络的误差和训练次数均低于BP神经网络，证明了RBF网络比BP神经网络更具优越性。

一系列研究表明，虽然使用神经网络预测所得到的结果与实验值比较接近，但是仍然存在一些不足。单一的神经网络预测模型存在预测时间长，模型不易收敛，容易陷入局部极小值等缺点。引入遗传算法是为BP神经网络的选择较优的初始权值和阈值，避免BP神经网络在训练时陷入局部极小值并且提高网络的收敛速度。本文采用遗传算法优化BP神经网络可以解决这些缺点并在预测时更加接近仿真温度值。

2 磨削温度场的数学模型

砂轮上的磨粒与工件接触，切削而产生点热源，将每一个与工件接触磨粒所产生的热源集合起来，最终形成面热源。模型如图1所示。假定它是一个持续而又均匀的面热源，其单位时间单位面积内发热量为［5～6］

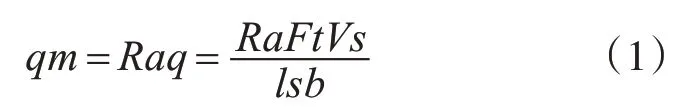
式中：ls为接触弧长；Ft为切向磨削力；Ra为热量分配比；Vs为砂轮速度；b为磨削宽度。

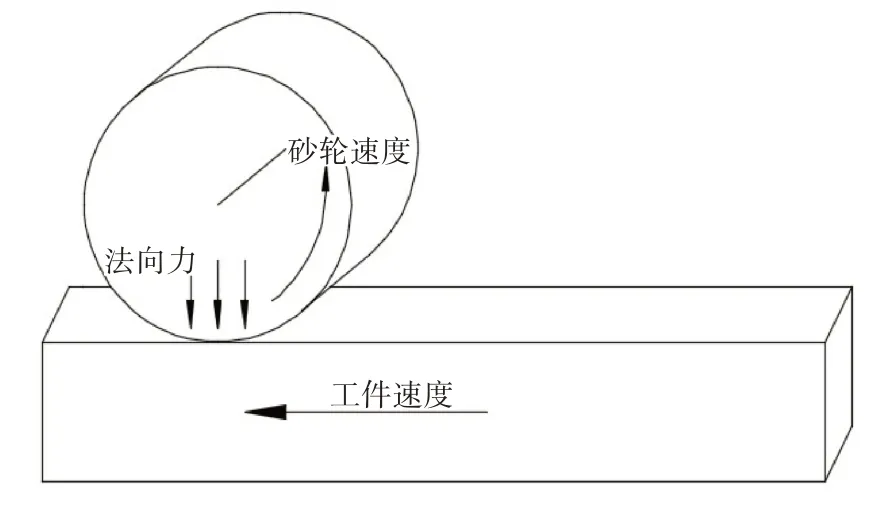
图1 平面传热模型

平面干磨条件下热量分配比［7］：

式中：λ1为工件的热导率；λ2为砂轮的热导率。

假设磨削过程中砂轮无磨损，砂轮与工件的接触弧长ls即为面热源的长度：

式中：ds为砂轮直径；ap为磨削深度。

磨削温度场是1个三维瞬态热传导问题，其场变量θ（x，y，z，t）在直角坐标中应满足如下微分方程［8］：

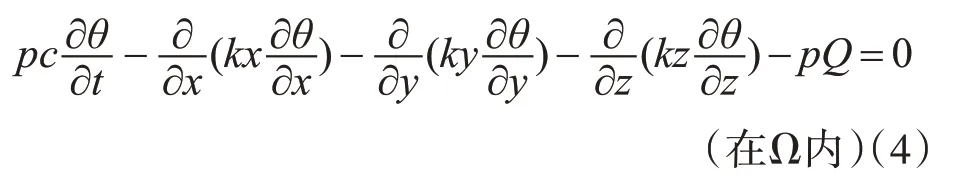
边界条件：

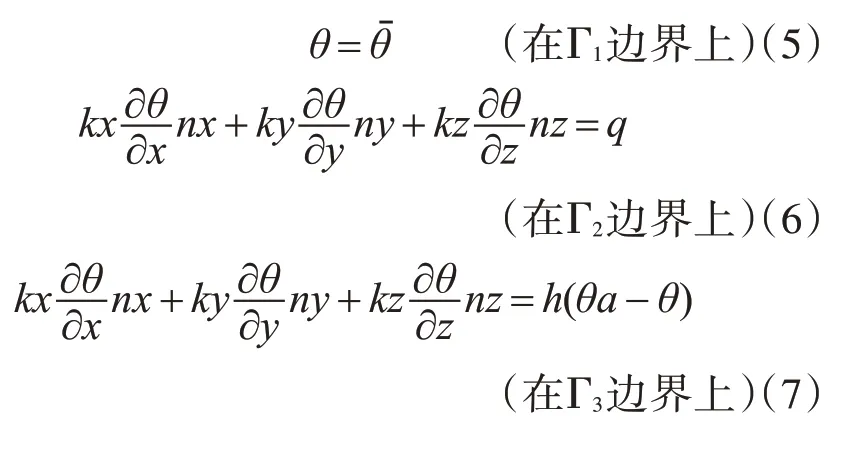
式中：p为材料密度；c为材料比热；t为时间；kx，ky，kz分别为材料沿x，y，z方向的热传导系数；Q（x，y，z，t）为物体内部的热源密度；nx，ny，nz为边界外法线的方向余弦；θˉ=θˉ（Γ，t）为Γ1边界上的给定温度；q=q（Γ，t）为Γ2边界上的给定热流量；h为放热系数；θa=θa（Γ，t）在自然对流条件下，θa是外界环境温度；在强迫对流条件下，θa是外界的绝热壁温度。边界应满足Γ1+Γ2+Γ3=Γ，其中，Γ是Ω域的全部边界。

3 磨削温度场有限元仿真

工件材料选择钛合金，磨削方式选用平面干磨削，磨削参数选择砂轮转速为25m/min、磨削深度为0.3mm、进给速度为30cm/s，冷却为空气自然冷却。由于磨削时间较短，且空气是热的不良导体，可以假定工件的表面是绝热的。由于磨削加工金属层较薄，所以发生相变的表层深度很浅，相变潜热带来的热量变化与磨削所产生的热量相比较小，所以忽略相变潜热带来的影响。取25℃的室温作为工件的起始温度。

工件性能参数以及边界条件及相关参数如表1、表2所示。

表1 工件性能参数

表2 边界条件及相关参数

创建一个长30mm、宽10mm、高4mm的实体模型，单元类型选用20节点的二次六面体八节点单元，即Solid90单元。然后进行网格划分。因为工件表层与深层的温度梯度相差较大，且工件表面会发生相变，对精度要求相对较高，所以要求工件表面的网格划分得更细更密。而精度要求随着深度增加反而将低，底层网格可以稀疏一些。图2所示为网格划分结果。经仿真得到第10时间步磨削温度分布图如图3所示，从图中可以看出工件表面温度最高达到213.166℃。

图2 网格划分结果

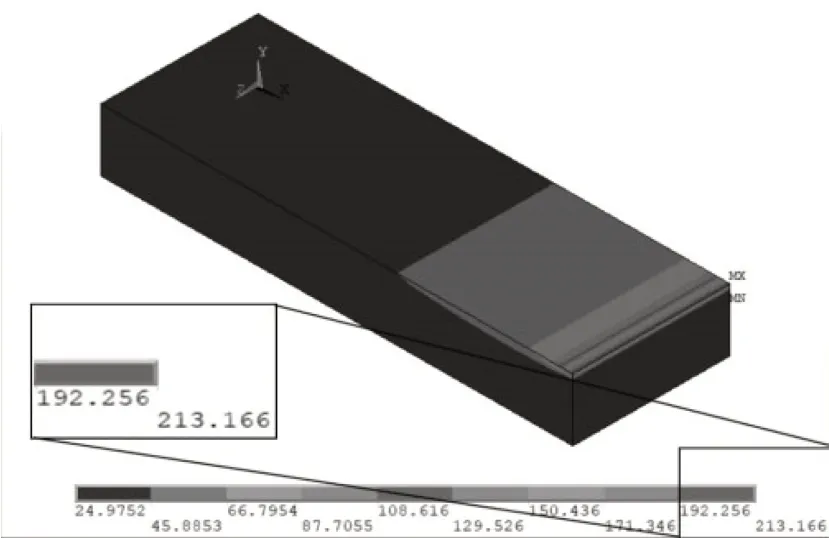
图3 第10时间步的温度分布图

4 基于GA-BP神经网络的磨削温度预测

4.1 表面温度预测模型的建立［9～10］

遗传算法能够在全局搜索最优值，为BP神经网络提供最优的初始权值、阈值。本文提出的磨削温度预测模型结构如图4所示，遗传算法主要内容如下：

1）种群设置：对初始种群及种群规模的设置，在所设范围内寻找最好的权值和阈值。本文初始种群规模为50。

2）对初始种群编码：选择合适的编码方案、长度等。本文编码方案为实数编码，编码长度为36。

3）选择适应度函数：适应度是唯一判断遗传算法优劣的标准。本文将预测输出和期望输出之间的误差平方和的倒数作为个体适应度。

4）遗传算子的设置：选择适应度较大的个体，并留到下一代；赋予合适的交叉和变异的概率。

对于BP神经网络，关键是输入节点和输出节点，隐层节点个数等的确定。

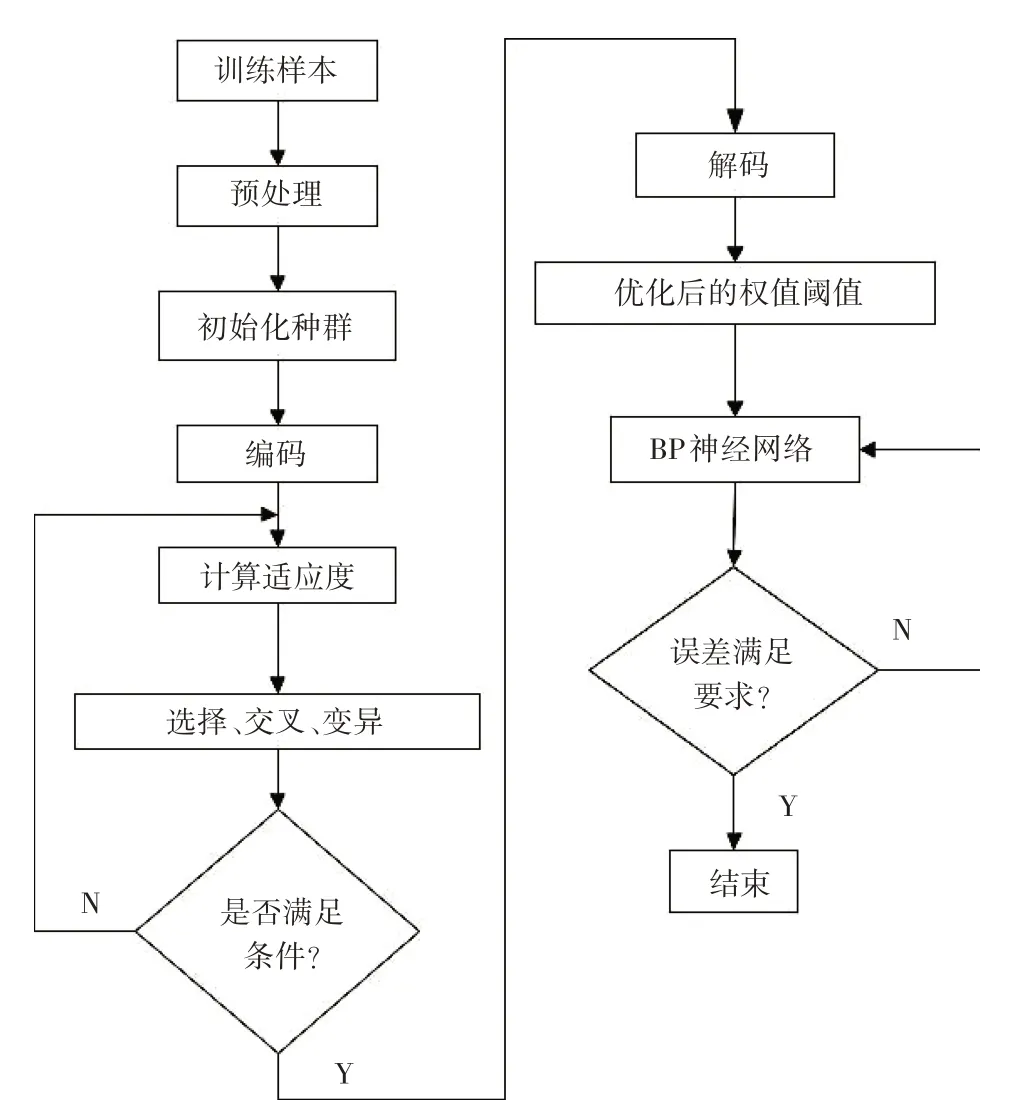
图4 GA-BP预测模型结构

4.2 网络层数的确定

BP网络属于多层前馈网络，数量较多的隐层能够提高网络的精度，但会增加训练时间并降低泛化能力［11］。因此，隐层层数应尽量较少，预测的精度可由隐层节点数量来保证。因此本文确立了单隐层的BP神经网络结构。

4.3 各层节点数

1）输入、输出层节点数

磨削加工中，有很多参数都会影响磨削温度的大小，而本文以工件转速、磨削深度和进给速度三个影响因数作为预测模型的输入，以磨削温度作为输出参数。因此神经网络模型输入层节点数为3，输出层节点数为1。

2）隐层节点数

目前，并没有统一的公式或者理念确定隐层节点数，一般通过比较模型预测的效果来确定BP网络隐层节点的个数［12］，输入节点数较少时，只能通过经验公式来确定隐层节点数。当输入节点较少时，隐层节点数的经验公式有［13］：

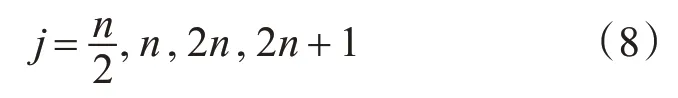
式中：j为隐层节点数，n为输入节点数。本文中输入节点数为3，则合适的隐层节点数为2，3，6，7。经试验比较，本文选择的网络结构为3-7-1［14］。

4.4 测试数据选取

采用仿真获得的温度值，如表3所示。随机选取其中的第5，8，14，17，20，23组数据作为测试样本不参加神经网络的训练，将其他数据输入网络进行训练，训练完成后，对选取的测试样本进行预测。

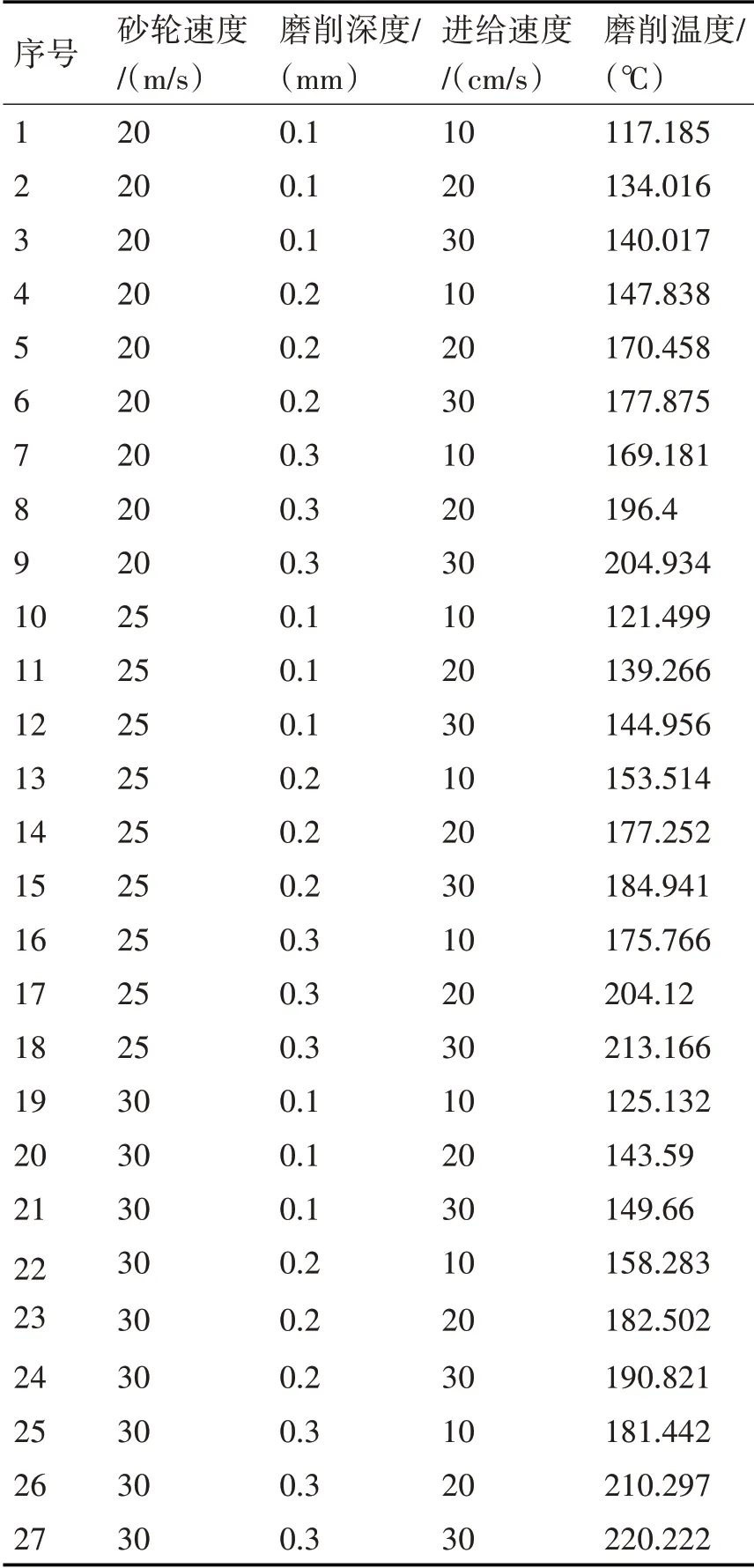
表3 训练及测试样本数据

4.5 磨削温度预测

利用Matlab工具箱‘GAOT’对遗传算法搭建与训练，BP神经网络部分自行编写。神经网络隐层神经元激活函数采用S型函数‘tansig’，输出层神经元激活函数采用线性函数‘purelin’，网络的训练函数采用LM函数，LM算法具有很快的收敛速度［15］。在图5所示的适应度曲线中，适应度随着遗传代数的增加逐渐变大，进行到35代左右，适应度达到一个较大值，说明样本对环境的适应度已经很高了。由于BP神经网络的初始权值和阈值已经经过遗传算法的优化，在对模型进行训练时，GA-BP模型收敛速度非常快，训练误差在第四步就已经达到最优值，结果如图6所示。将抽取的测试样本输入网络，结果如表4所示。BP神经网络预测值平均相对误差为3.37%，GA-BP预测值的平均相对误差为1.85%。

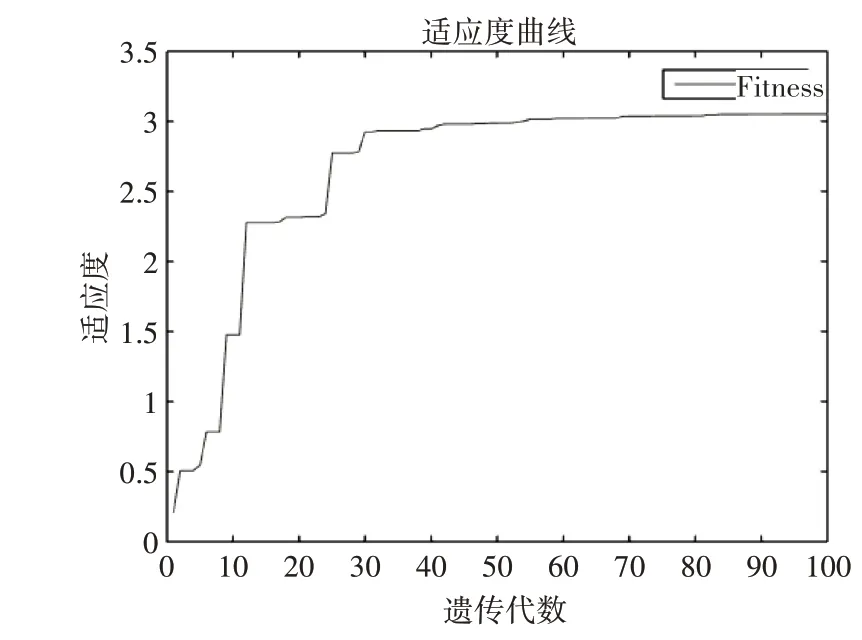
图5 适应度曲线

图6 网络训练结果

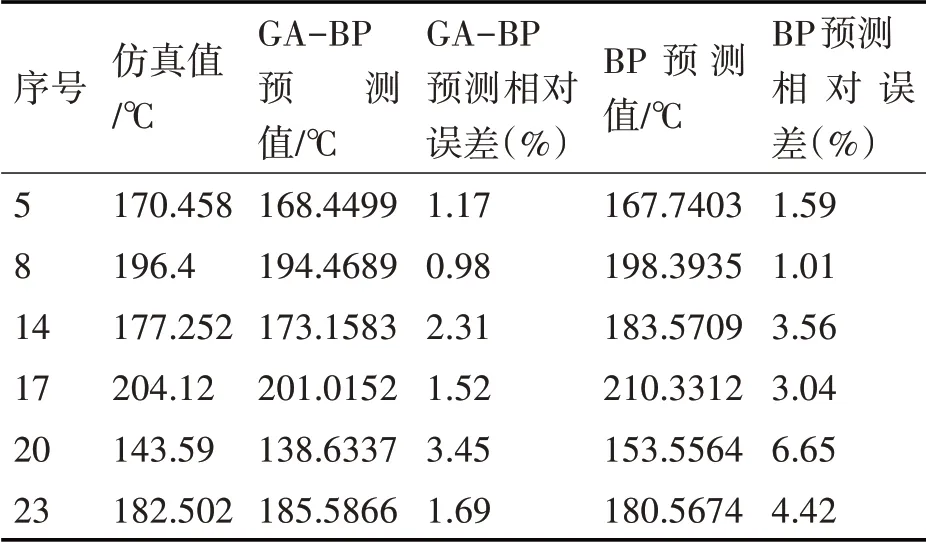
表4 磨削温度预测值

4.6 磨削温度预测系统设计

本文使用Matlab语言设计开发了简易的磨削温度系统。系统主要有两个部分构成：第一部分为系统说明以及参数显示；第二部分为BP和GA-BP神经网络的温度预测显示。系统界面如图7所示。

此系统便于操作人员提前获知较为准确的磨削加工的最高温度，并与以往实际磨削加工的温度以及操作经验进行比较来判断是否需要调整磨削参数来降低温度。这样便能够提高了操作效率以及生产效率，并降低损失。

图7 磨削温度系统

5 结语

本文利用有限元仿真得到了磨削温度场的分布情况，并且采用BP和GA-BP预测模型对磨削温度进行了预测，通过比较表明了GA-BP预测模型具有较高的准确性，也证明了在预测磨削温度方面的可行性。

在此基础上开发出来的磨削温度预测系统可以对操作人员有更好的帮助。因此对GA-BP神经网络预测模型应用到实际生产加工中有一定的理论指导作用。