云计算任务调度双精英种群文化基因改进算法∗
2021-06-02杨春花
杨春花 刘 娟
(乌鲁木齐职业大学信息工程学院 乌鲁木齐 832000)
1 引言
云计算是一种通过虚拟化技术将所需要的各种资源以任务的形式整合在虚拟资源池上,以便于使用者能够根据自身需求来获取相应的服务[1]。云计算环境中存在着诸多不同类型的计算任务,基于某种需求,若任务调度不够优化,会浪费整体的计算时间并且降低资源利用率。云计算资源调度问题的核心内容在于如何有效运用资源,提高云计算的计算效率,缩短计算时间。云计算任务调度需要同时兼顾计算效率和资源利用率。显然,这两个优化目标之间存在着一定的矛盾性,会增加问题优化的难度。此外,云计算在实际的计算过程中,不仅能处理计算任务规模较小的优化任务,同时,也应针对任务量较大的优化任务,具有较高的运算能力和求解效率。但云计算通常随任务量的增加,难度成几何倍增长。由此可知,现实中的云计算任务调度问题极难求得令人满意的解。
针对上述问题,国内外的研究学者提出了不同方式的云计算资源调度算法,其中占主流的方式为通过智能优化算法对云计算资源调度模型进行优化,在提高计算速度的同时,更加有效地节约计算所需资源。文献[2]提出一种基于改进粒子群算法的云计算资源调度策略,提高了云计算的计算速度。针对云计算中的任务调度问题,查英华[3]等提出了一种任务调度的增强蚁群算法。针对云计算环境下内置任务调度方法的低效问题,申丽君[4]等提出一种基于改进免疫进化算法的任务调度算法。为提高基于人工智能算法在优化云计算资源调度模式时,出现资源利用率低的问题,卓涛[5]等通过将随机向量策略引入到人工蜂群算法中,提高算法的收敛精度。此外的求解方法还有布谷鸟搜索算法[6]、基于改进惯性权重的粒子群算法[7]、模糊聚类算法[8]、蚁群优化-蛙跳算法[9]和改进贪婪算法[10]。上述优化策略均是通过单一策略对人工智能算法进行改进,在优化具有任务量较大的云计算任务时,算法的优化精度并不高,难以平衡资源利用率和计算时间。
针对上述问题以及云计算资源调度模型的特点可知,采用传统的人工智能算法难以求得最优解。同时,针对具有单一改进策略的人工智能算法而言,改进后的算法往往难以平衡算法的全局搜索能力和局部勘探能力,导致算法在迭代后期早熟收敛。针对此问题,本文基于兼顾考虑计算时间成本和资源花费成本的云资源任务调度优化模型,提出了一种云计算任务调度双精英种群文化基因算法。为了验证本文所提改进算法的有效性和高效性,本文针对改进算法进行了测试函数对比试验和实际算例的仿真对比实验,试验结果表明,本文提出的文化基因改进算法具有更佳的算法性能。
2 云计算任务调度问题的优化模型
云计算任务调度问题是一个多目标的优化调度问题。其中两个优化目标分别为计算时间成本最小和资源花费成本最低[11]。云计算的计算过程中,需考虑在最短时间得到最优结果,同时云计算任务调度需要兼顾考虑计算资源的合理配置,计算节点使用的不平衡程度能够反映计算资源的配置情况。因此,将计算时间成本最小记为Tmax,资源花费成本最低记为Bdegree。具体的云计算资源调度优化模型为

式(2)中,M={1 ,2,3…m}为任务集合,含m个不同的任务;N={1 ,2,3…n}为计算所需全部节点,其中节点个数为n;tij表示第i个任务在第j个计算节点上执行所花费的时间成本;eij是决策变量,为第j个计算节点上执行第i个任务,若是,则eij=1,否则,eij=0。
最大任务的执行时间Tmax采用下述公式计算得到:
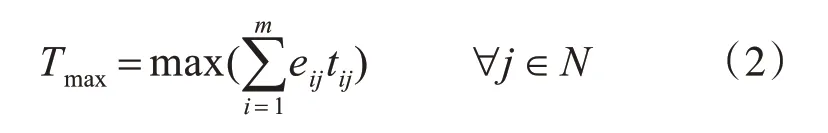
不平衡程度Bdegree的数学表达式如下所示:

式(3)中,enum={e1,num,e2,num,…,en,num}为节点几何中n个不同节点执行次数的集合,E(X)为集合X的方差。
上述优化模型求得最优需使得任务完成时间最短,即:

式中,cost为最短的任务完成时间。
3 改进的文化基因算法
3.1 文化基因算法
文化基因算法是Pablo Moscat于1989年首次提出的一种模拟文化进化的群智能算法[12]。它是一种基于种群的全局搜索与基于个体的局部启发式搜索相结合的混合优化算法,其与遗传算法有着较大的类似。
为提升文化基因算法的优化性能,本文提出了一种文化基因改进算法,记为IMA(Improved Me⁃metic Algorithm)。通过混合全局搜索策略提高算法的全局搜索能力。通过引入模拟退火策略和爬山算法提高算法的局部开发能力。
3.2 粒子群算法
粒子群算法是模拟鸟群捕食的仿真优化算法[13]。设种群规模为N,维数为D,第i个粒子的坐标位置向量为,速度向量为,个体极值为,粒子群全局极值记为
基本粒子群群算法更新迭代计算公式如式(5)所述。
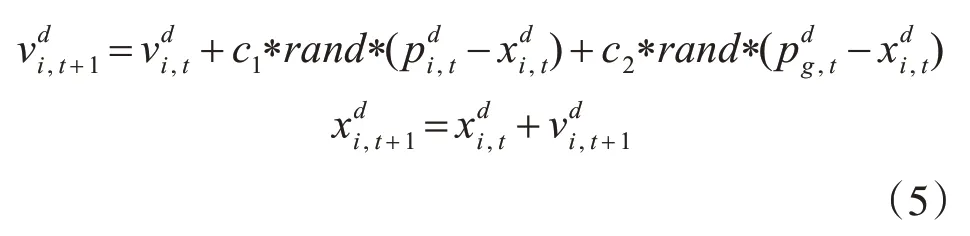
式中i=1,2,…,N,t为维度,d表示迭代次数,c1,c2为随机权重,rand为0~1之间的实数。
3.3 遗传粒子群算法
粒子群算法因其具有强大的全局搜索能力,故而适合于作为文化基因全局搜索的搜索算法。由粒子群算法的迭代计算公式可知,粒子群算法在求解过程中,全部的个体均受局部极值点的吸引,朝局部极值点的方向进行移动,不利于其保持种群多样性。相比于粒子群算法,遗传算法在保持种群多样性上有明显的优势,遗传算法在迭代过程中,通过交叉变异的方式,不断生产新的个体,并不断对种群中的全部个体进行贪婪选择,使得算法的迭代过程中,不会丧失种群多样性。因此本文将遗传进化机制引入粒子群算法中。具体的遗传粒子群算法的计算步骤如图1所示。
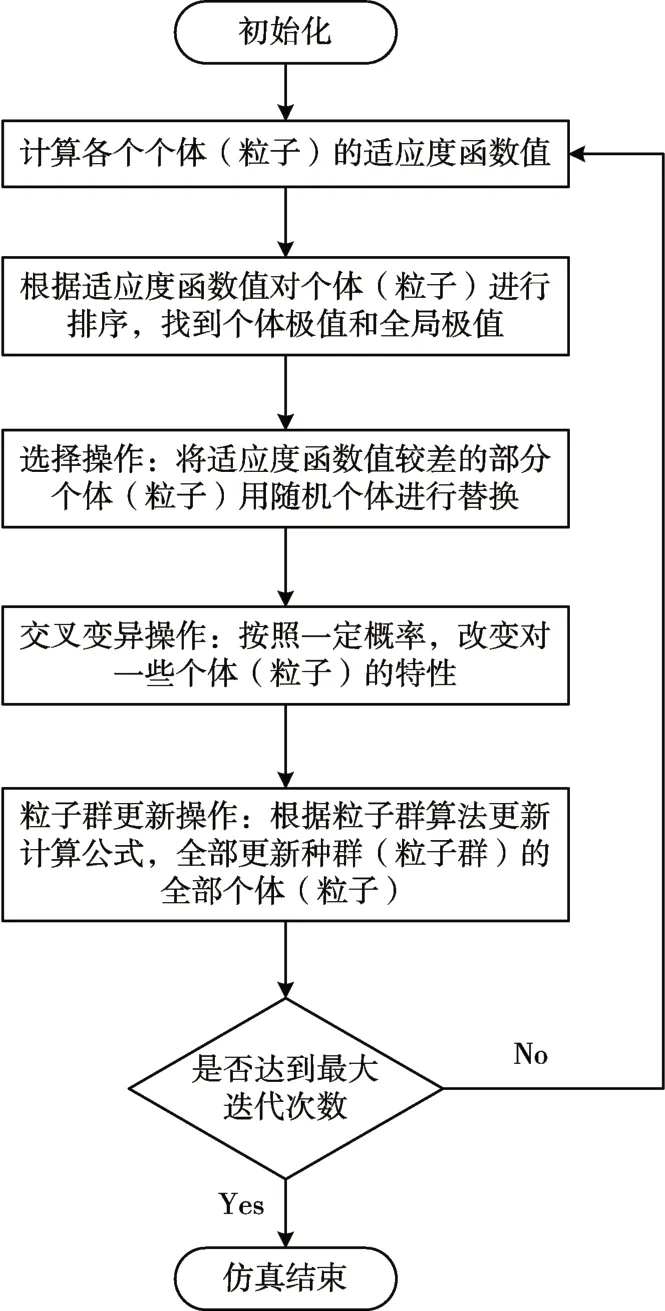
图1 遗传粒子群全局搜索算法
3.4 双精英种群进化机制
由于进化环境和初始种群都有一定的局限性,经过相当长时间以后,精英群体因其长期进化而积累一定的自身优势,从而对整个种群形成了一定程度的“统治”。此时,整个种群就会显现出进化缓慢或停滞的不利状态,这种状态也被称之为平衡状态。为此,本文通过双精英种群策略对其进行改进。双精英种群进化机制是一种并行机制,它使两个精英种群同时进化,并在迭代过程中不断进行信息交互,将每次迭代所产生的最优个体保存在其中一个种群中,将适应度值较差的个体保存在另外一个种群中,从而跳出局部最优[14]。具体的双精英种群最优粒子被交换的示意图如图2所示。
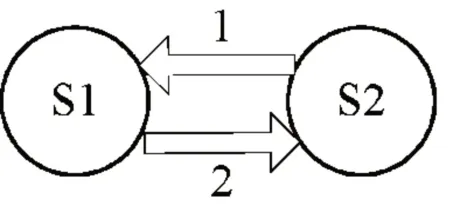
图2 双精英种群最优粒子被交换的示意图
双精英种群文化基因算法进化流程如下所述:
Step1:初始化文化基因种群,规模为m。
Step2:计算种群中全部个体的适应度函数值。
Step3:对种群中全部个体按适应度值大小进行排序,求解到局部极值点和当前全局极值点。
Step4:采用遗传粒子群算法对整个种群进行全局搜索。先将遗传算法中的选择、交叉、变异算子作用于整个种群的全部个体,然后将粒子群更新规则作用于整个种群的全部个体。
Step5:选择种群中m个个体中的2N个精英个体以构成两个精英种群,分别记为精英种群1和精英种群2。
Step6:采用爬山算法和模拟退火算法对两个精英种群进行局部搜索。精英种群1采用爬山算法进行进化,精英种群2采用模拟退火算法进行进化。
Step7:分别计算两个精英种群的各个精英的适应度函数值。
Step8:两个粒子群进行信息交流,也即交换其最优粒子。
Step9:判断是否达到最大迭代次数,是则转为Step10,否则转为Step2。
Step10:将迭代计算的优化结果输出。
3.5 爬山算法和模拟退火算法
爬山算法是一类具有较强局部开发能力的人工智能优化算法,算法在求解过程中,通常从当前最优解出发,通过尝试改变当前最优解的位置寻求适应度值更高的最优解,并在迭代过程中不断进行贪婪选择,直到达到最大迭代次数,输出当前求解的最优解[15]。
模拟退火算法(SA)最早由Kirk-patrick等应用于组合优化领域。模拟退火算法基于金属热力学降温过程,在这个降温过程中不断产生新解并根据Metrolips准则来判断是否接受该解,从而最终获得更佳的优化解。
爬山算法和模拟退火算法都是一种局部搜索能力很强的优化算法,因而适合作为文化基因算法的局部搜索算法。
4 仿真实验
4.1 基于测试函数的仿真对比
本文采用两种不同的测试函数对本文提出的改进的文化基因算法(IMA)、全局搜索采用粒子群算法且局部搜索采用模拟退火算法的普通文化基因算法(MA)和粒子群算法这三种不同的智能优化算法进行对比测试。以下是具体的测试结果。
1)De jong函数,极值点为0.0。De jong函数的数学表达式为
具体的De jong函数的仿真测试结果如图3和表1所述。
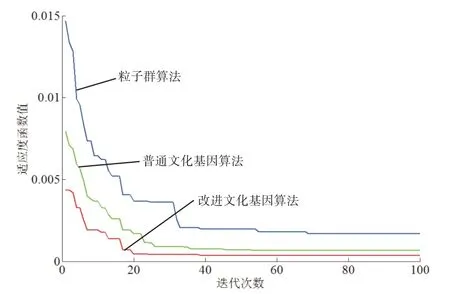
图3 采用De jong函数的仿真测试收敛曲线
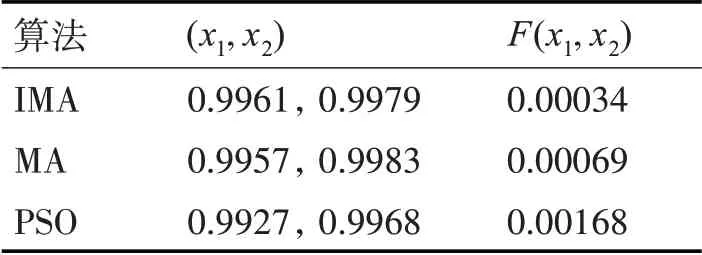
表1 采用De jong函数的仿真测试结果
由图3和表1可知,相比其他两种算法而言,本文所提改进文化基因算法(IMA)求解的结果最优,寻优得到的最优解为(x1,x2)=(0.9961,0.9979);最优解函数值为F(x1,x2)=0.00034。
2)Schaffer函数,极值点为0.0。其数学表达式为
具体的Schaffer函数的仿真测试结果如图4和表2所述。

图4 采用Schaffer函数的仿真测试收敛曲线
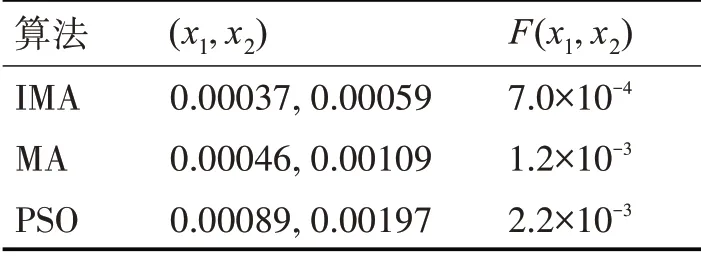
表2 采用Schaffer函数的仿真测试结果
由图4和表2可知,本文所提改进文化基因算法(IMA)的求解结果同样最优,寻优得到的最优解为(x1,x2)=(3.7×10-4,5.9×10-4);最优解函数值为F(x1,x2)=7.0×10-4。
4.2 基于实际算例的仿真对比
本文采用云计算任务调度问题的实际算例对本文提出的改进的文化基因算法(IMA)和普通文化基因算法(MA)这三种不同的粒子群算法进行对比测试。本文选用的云计算任务调度问题的实际算例有4个计算节点和10个任务。以下是具体的测试结果。
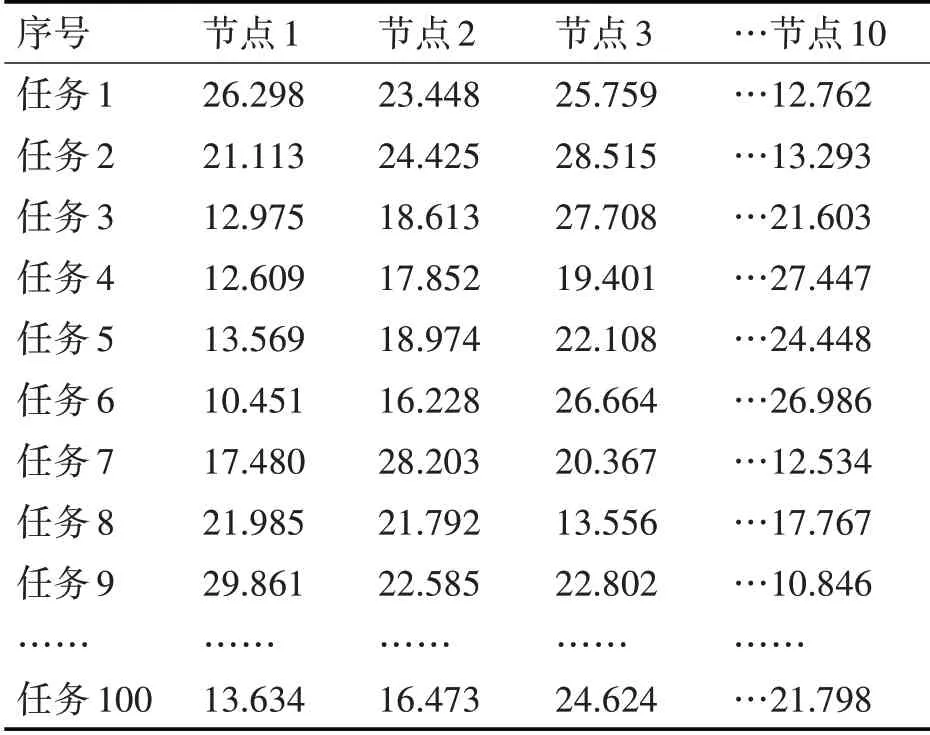
表3 云计算任务调度问题的估算执行时间表
具体的云计算任务调度问题的寻优收敛曲线如表4图5和图6所述。

表4 云计算任务调度问题优化的仿真测试结果
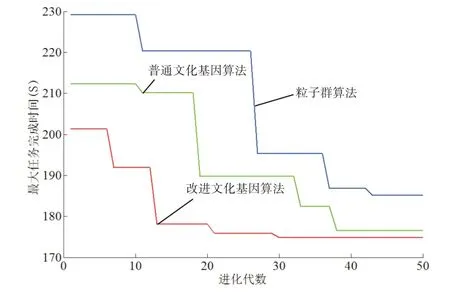
图5 云计算任务调度问题最大任务完成时间的寻优收敛曲线
由图5和图6可知,相比于其他算法,文化基因改进算法(IMA)最优,求解得到的任务执行节点序列为e=[7 6 8 7...9,]估算的最大任务完成时间为174.7872。与此同时,粒子群改进算法(IPSO)寻到的计算节点使用的不平衡程度最小,为0.4444,其任务执行节点序列各个节点执行次数的集合为
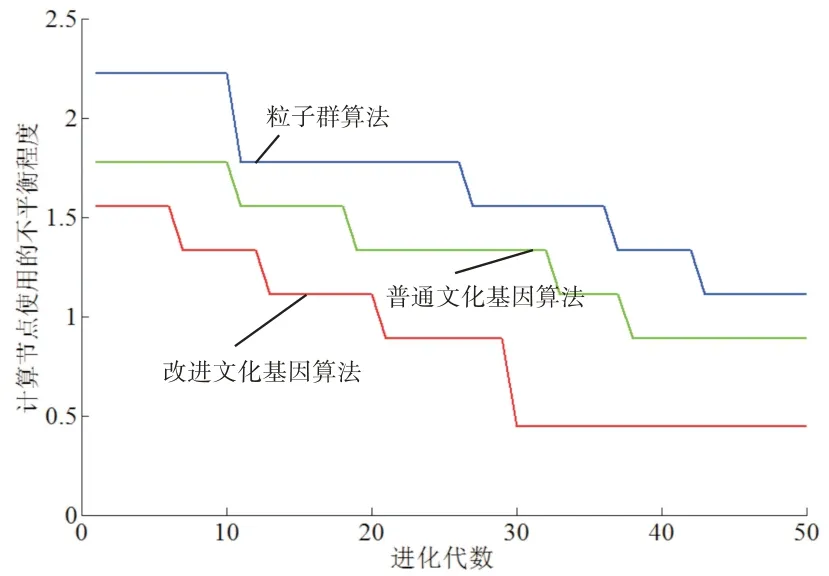
图6 云计算任务调度问题计算节点使用的不平衡程度的寻优收敛曲线
5 结语
本文基于云计算任务调度问题的优化模型,提出了一种基于双精英种群文化基因改进算法。首先,在粒子群算法的基础上,引入了遗传进化机制,以便于更好地维持种群多样性,从而提升其全局搜索算法全局收敛的性能;其次,为一定程度地抑制文化基因算法陷入平衡状态不易优化的缺陷,本文通过双种群精英策略对其进行改进,提高算法的局部开发能力,防止算法在迭代后期陷入局部最优,早熟收敛。最优,本文通过测试函数对比试验和实际算例仿真实验,以时间花费和资源花费为目标函数,对本文所提改进文化基因算法分别进行验证。从实验结果可知,本文提出的文化基因改进算法的寻优性能更佳,能够更有效地解决云计算任务调度问题。
