一种深度降噪自编码器的语音增强算法∗
2021-06-02刘鹏
刘 鹏
(山西工程技术学院信息工程与大数据科学系 阳泉 045000)
1 引言
传统的语音增强算法(如子空间法、谱减法和维纳滤波法),作为一种非监督方法大都基于语音和噪声信号复杂的统计特性来实现降噪,但在降噪过程中不可避免地会产生“音乐噪音”,导致语音失真[1]。考虑到噪声对清晰语音产生影响的复杂过程,在带噪语音与清晰语音信号间基于神经网络建立非线性映射模型来实现语音增强已成为当前研究的一个热点。
Xugang Lu,Yu Tsao等学者采用逐层预训练(layer-wise pre-training)堆叠自编码器(Stacked AutoEncoder)后微调(fine tuning)整个学习网络的方法,建立了深度降噪自编码器(Deep Denoising AutoEncoder,DDAE),完成了带噪语音的降噪,并验证了增加降噪自编码器的深度,有助于提高语音增强的效果[2]。但是,由于深度降噪自编码器是对训练集中带噪语音与清晰语音对的一种统计平均,在缺乏足够样本量的数据集上进行训练,极易产生神经元的联合适应性(co-adaptations),进而导致过拟合。为此,文献[3]提出了DDAE的集成模型(Ensemble Model),将训练数据聚类后分别训练多个DDAE模型,然后在训练数据集上通过回归拟合来建立多个DDAE的组合函数。但是,集成模型需要训练和评估多个DDAE模型,这将花费大量的运行时间和内存空间。研究表明,集成模型通常只能集成5~10个神经网络,超过这个数量将很快变得难以处理[4]。Yong Xu,Jun Du等学者选用Dropout训练的深度神经网络(DNN)模型实现了带噪语音增强。选用Dropout训练所得的深度网络可以看作是每轮训练所得网络的集成,但由于Dropout所引入的噪声扰动(perturbations)在一定程度上破坏了带噪语音中噪声的特性关系,因此完全采用Drop⁃out训练对于测试数据集噪声类型与训练集相同的情形,增强效果不佳[5]。研究表明[6~7],带噪语音中不同类型语音分段(segment)对语音整体的可懂度影响不同,中均方根分段(短时信噪比小于整体均方根但不小于-10dB整体均方根的分段)影响了带噪语音整体的可懂度。因此,我们提出了基于语音分段类型来分类训练DDAE模型的语音增强算法。
本文算法首先将训练数据集的带噪语音与清晰语音对进行短时分段处理后,划分为中均方根分段训练子集和非中均方根分段训练子集。然后,中均方根分段训练子集选用Dropout方法训练DDAE(即随机选出部分神经元参加训练),非中均方根分段训练子集选用非Dropout方法训练DDAE(即所有神经元均参加训练)。这样,使得训练好的DDAE模型既可以减少Dropout所引入的扰动对带噪语音噪声特性的破坏又可以增强对带噪语音可懂度关键分段(中均方根分段)语音特性学习的鲁棒性,避免陷入过拟合,提高了语音可懂度增强的效果。
2 理论概述
2.1 深度降噪自编码器
自编码器(AutoEncoder,AE)是一种以无监督的方式来学习数据编码的人工神经网络。如图1所示,自编码器的网络结构特点是输入层神经元数目和输出层相等,隐藏层神经元数目小于输入层和输出层,网络学习是以重构自身输入为目的(而不是预测目标值),通常用于数据降维和特征提取。自动编码器总是由两部分组成:编码器和解码器。它们可以被定义为式(1)所示的转换,其中X是输入数据集,Z是压缩编码,X′为输出数据集,ϕ是编码转换,ψ是解码转换。
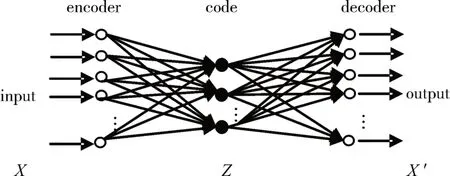
图1 自编码器的网络结构
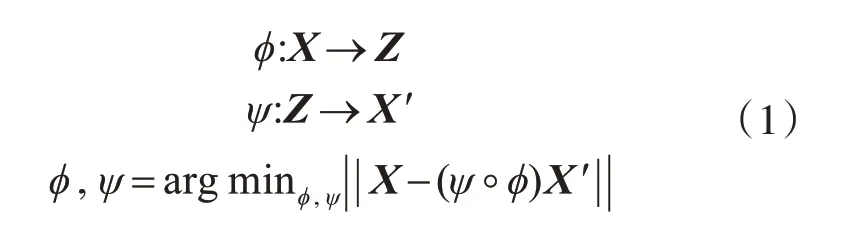
降噪自编码器(Denoising AutoEncoder,DAE)是针对部分输入数据中含有噪声的情形,训练的目的是尽量输出不含噪的输入数据,以增强自编码器所提取的数据特征对所加入噪声的鲁棒性。因此,DAE的模型训练可分为四步。
1)加入噪声:将原有输入数据x加入某种形式的噪声后得到带噪数据x͂。
2)编码:将带噪数据x͂作为输入层数据经过式(2)转换到隐藏层。其中,z是编码数据,W是编码权重矩阵,b是编码偏置向量,σ是编码激活函数(这里选取为sigmoid函数)。

3)解码:将隐藏层数据经过式(3)转换到输出层。其中,′是输出数据(降噪后数据),W′是解码权重矩阵,b′是解码偏置向量,σ′是解码激活函数(这里选取为sigmoid函数)。

4)确定并最小化损失函数:降噪自编码器经过训练以尽量减少输出数据(降噪后数据)与原有输入数据的差别,训练目标同样是使损失函数最小化。降噪自编码器的损失函数可参照式(4)和式(5)确定。

Xugang Lu,Yu Tsao等学者在DAE模型的基础上采用逐层预训练的方式,将多个自编码器堆叠后微调整个学习网络,建立了深度降噪自编码器(DDAE)模型。实际上,DDAE模型在本质上也是一种深度神经网络(DNN),已有学者基于DNN模型开展了语音增强研究[8~10],因此,同样可以选用Dropout训练方式来快速训练DDAE模型。
2.2 Dropout训练
Dropout训练是在DNN训练开始前固定一组超参数来随机决定网络中的神经单元(输出单元除外)是否包括在本轮训练的网络中,通常一个输入神经元被包含在本轮训练网络的概率为0.8,一个隐藏神经元其相应的概率为0.5[4]。因此,Dropout训练的结果是原有DNN子网络的集成,而且,在训练过程中共享了模型参数。Dropout训练可以降低神经元的联合适应性(co-adaptations),在某种程度上,它避免了模型产生过拟合。Dropout训练之所以有效在很大程度上得益于它给隐藏单元所带来的掩码噪声(masking noise),这在一定程度上相当于增加了训练数据集的规模[4]。
3 基于语音段分类训练DDAE增强算法
3.1 模型概述
本文所提出的基于语音段分类训练DDAE模型的语音增强算法框架如图2所示,这一系统由训练和增强两个阶段构成。
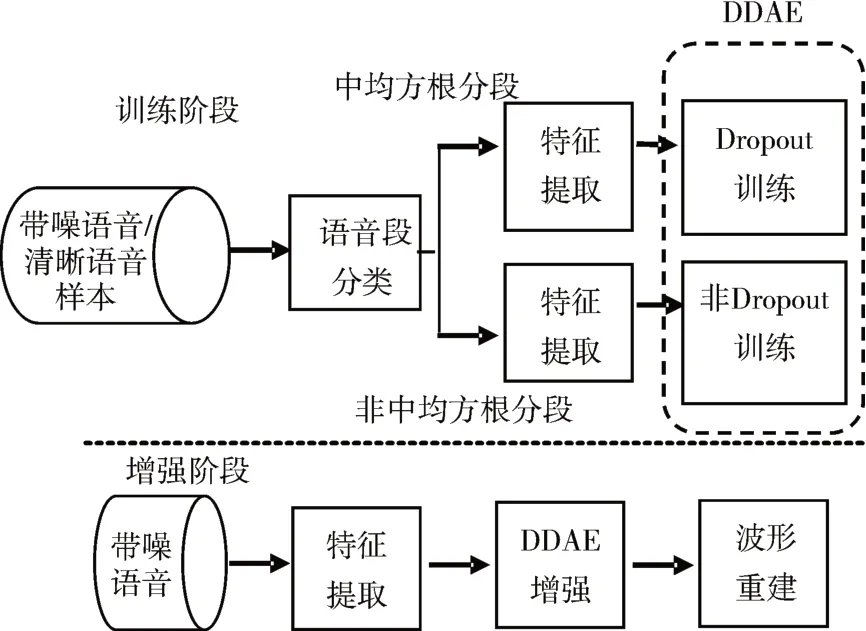
图2 基于语音段分类训练DDAE增强算法框架
在训练阶段,采用DDAE作为从带噪语音特征到清晰语音特征的映射函数。训练阶段的具体工作如下。
1)将训练集中的带噪语音与清晰语音样本对进行短时分段处理后,按照语音分段短时信噪比与整体均方根的关系,将原有训练数据集重新划分为中均方根分段训练子集和非中均方根分段训练子集。
2)将训练子集中带噪语音分段与清晰语音分段进行快速傅里叶变换后,提取其频谱的对数幅度特征,分别作为DDAE模型的输入与输出。
3)在依据语音分段的不同类型所构建的两种训练子集上开展DDAE模型训练。中均方根分段训练子集选用Dropout方法训练,非中均方根分段训练子集选用非Dropout方法训练。
在增强阶段,利用训练好的DDAE模型对带噪语音特征进行处理,预测出清晰的语音特征,进而波形恢复出清晰语音,实现语音增强。增强阶段的具体工作如下:
1)将测试集中的带噪语音进行短时分段处理后,提取带噪语音分段的频谱对数幅度特征。
2)将所提取的带噪语音分段的频谱对数幅度特征,作为已训练好的DDAE模型的输入值,通过DDAE模型获得相应的输出值,即增强后语音分段的频谱对数幅度特征。
3)将增强后语音分段的频谱对数幅度,结合带噪语音的相位信息,依据文献[5]中的方法完成增强语音的波形重建。
3.2 语音段分类
将训练集中的带噪语音与清晰语音样本对加窗进行短时分段处理(本文中窗长16ms,重叠50%)。假设带噪语音中的语音信号稳定,噪声信号与语音信号无关,按照式(6)计算带噪语音分段m的先验信噪比ξ(m)。
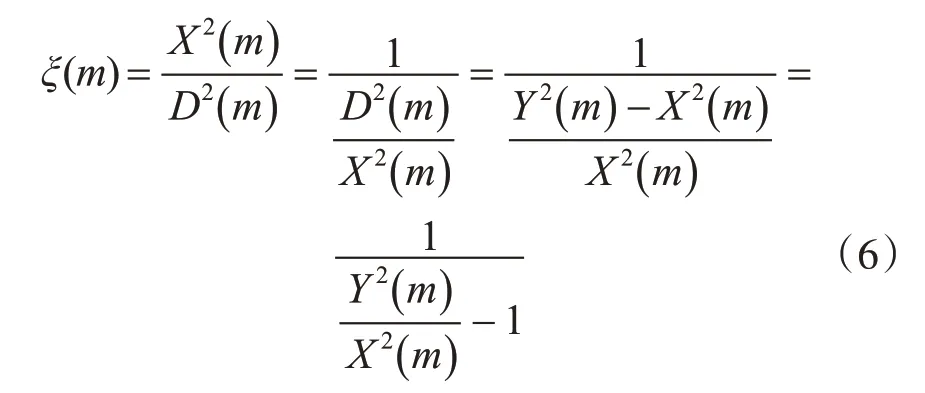
其中Y(m)为带噪语音的功率,X(m)为与之对应的清晰语音的功率,D()m为噪声信号的功率。带噪语音分段先验信噪比的相对均方根依据式(7)计算得出,M为带噪语音的分段个数。
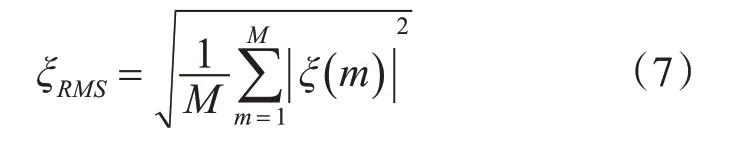
最后,依据式(8)确定出带噪语音短时分段中的中均方根分段,进而将训练集划分为中均方根分段训练子集和非中均方根分段训练子集。

3.3 基于语音段分类训练的DDAE模型
本文中的DDAE模型由1个输入层,5个隐藏层(每层500个神经元)和1个输出层构成。DDAE模型的输入向量和输出向量分别如式(9)和式(10)所示。其中,和分别表示输入和输出的第m帧第k个频带的谱幅度。
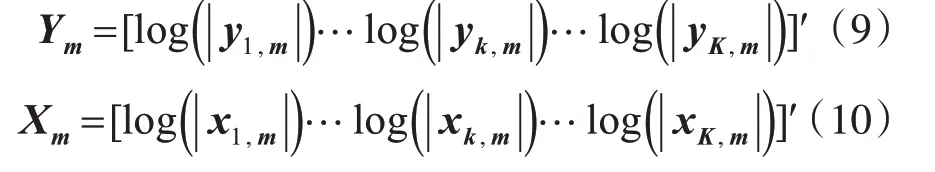
为了将两种训练方式在同一个DDAE模型上实现,模型基于Inverted Dropout进行了改进训练,在训练阶段其正向传播的过程如式(11)所示。
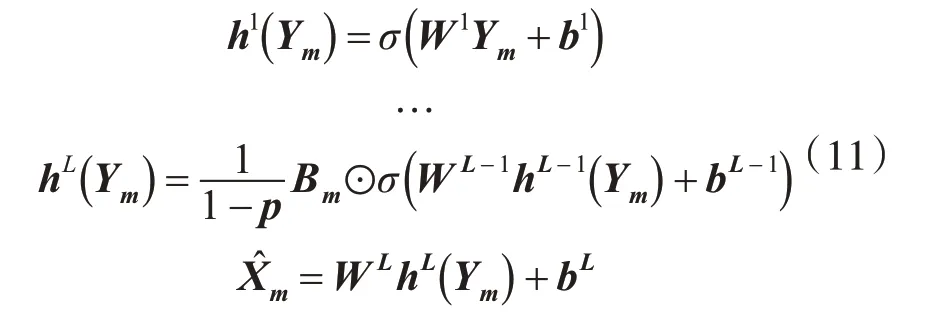
其中,p为Dropout训练中神经元的舍弃概率,当选用Dropout方式训练时p=0.5,当选用非Dropout方式训练时p=0。Bm是如式(12)所示的m维向量。
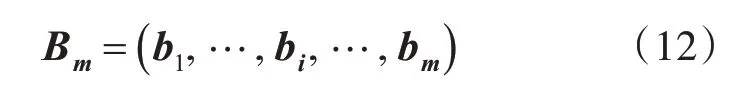
当选用Dropout方式训练时Bm中的各元素bi是伯努利(Bernoulli)随机变量,其取值为0的概率是p,其取值为1的为概率是1-p;当选用非Drop⁃out方式训练时bi的值均为1。式(11)中σ(.)为Logistic sigmoid激活函数。DDAE模型的损失函数按照式(13)定义。
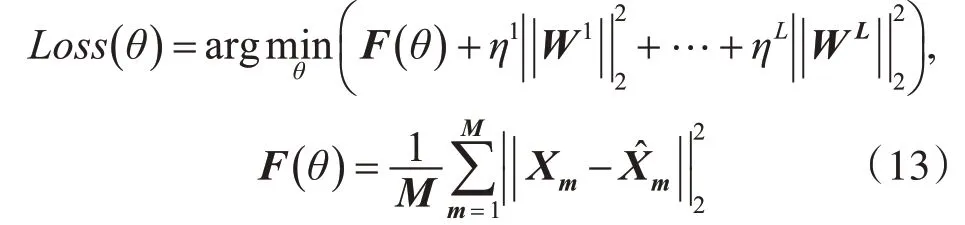
在语音增强阶段,已经完成参数训练的DDAE模型的正向传播过程如式(14)所示。

其中,为测试集中带噪语句m分段频谱的对数幅度,为使用分类训练好的DDAE模型增强后的语音频谱对数幅度。
4 实验结果与分析
为研究所提出算法对带噪语音可懂度的增强效果,基于TensorFlow深度学习框架开展了仿真实验。清晰语音材料来源于IEEE句子库[13],背景噪声选用NOISEX-92标准库中的babble,car,street和train四种噪声类型,实验中分别以-15dB、-10dB和-5dB三种信噪比加入噪声。实验中信号的采样频率统一在8Kz,量化精度为16bit。
实验中训练集由IEEE句子库的60组句子(共600个句子),按照12种加噪条件(4种噪声类型×3种信噪比)产生的带噪语音和对应的清晰语音构成。因此,训练数据集共有12个加噪条件子集,每个加噪条件子集有600个样本对,共计7200个样本对。
实验中测试集由IEEE句子库的剩余12组句子(共120个句子),按照12种加噪条件(4种噪声类型×3种信噪比)产生的带噪语音组成。因此,测试数据集共有12个加噪条件子集,每个加噪条件子集有120个样本,共计1440个样本。
4.1 语音可懂度评价
语音可懂度评价选用归一化协方差(Normal⁃ized Covariance Metric,NCM)评价法[14]。实验中把测试阶段样本处理后的归一化协方差NCM平均值作为其相应条件下语音可懂度评价值。为了进行实验效果的对比,选取了子空间法和原有DDAE方法(每轮训练中所有神经元均参加训练)对测试集中的样本数据进行了语音增强,并将其增强语音与本文算法增强语音的可懂度进行了对比。表1~表3给出了实验中语音可懂度的NCM评价结果。
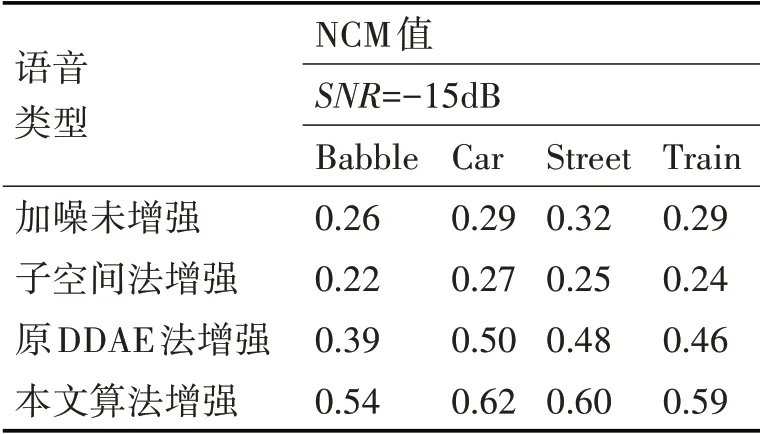
表1 信噪比SNR=-15dB,不同条件下语音的NCM值
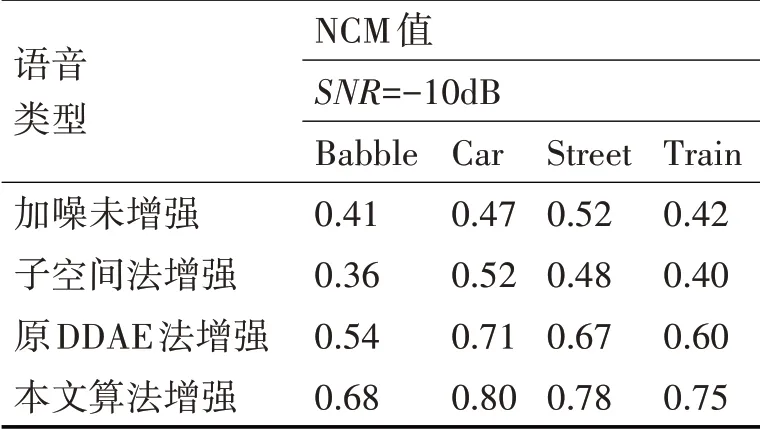
表2 信噪比SNR=-10dB,不同条件下语音的NCM值

表3 信噪比SNR=-5dB,不同条件下语音的NCM值
4.2 可懂度评价结果分析
带噪语音的NCM数值越大说明其主观可懂度越高[15],从表1~表3语音NCM测试值的对比可以看出:本文算法处理相较于其他三种对带噪语音的处理(加噪未增强,子空间法增强和原有DDAE法增强)提高了增强后带噪语音的可懂度。
由于中均方根分段影响了带噪语音整体的可懂度,中均方根分段训练子集选用Dropout方法训练DDAE,这相当于增加了此种训练数据集的规模,降低了神经元的联合适应性,在一定程度上防止了DDAE模型陷入过度拟合,使得语音可懂度的增强效果得以提高。
5 结语
本文提出了一种基于语音分段来分类训练DDAE模型的语音增强算法。该算法首先将训练数据集的带噪语音与清晰语音对进行短时分段处理后,划分为中均方根分段训练子集和非中均方根分段训练子集。然后,中均方根分段训练子集选用Dropout方法训练DDAE(即随机选出部分神经元参加训练),非中均方根分段训练子集选用非Dropout方法训练DDAE(即所有神经元均参加训练)。使得DDAE模型在尽可能减少Dropout所引入的扰动对带噪语音噪声特性破坏的同时,提高了对带噪语音可懂度关键分段(中均方根分段)语音特性学习的鲁棒性,提高了增强语音的可懂度。在模型实验中,选取了NCM评价法将本文算法在语音可懂度性能上开展了实验验证。结果表明,本文算法有效提高了增强语音的可懂度。
值得注意的是,虽然选用Dropout训练在一定程度上相当于增加了训练数据集的规模,但是,当训练集的样本数量极少时,同样有可能会导致Dropout失效[4]。我们将在后期对本文算法训练集的最小规模进行实验探究。
