基于混合蚁群分布估计算法的可重入流水车间调度∗

钟臻怡 杨家荣 吕 伟

（上海电气集团股份有限公司中央研究院 上海 200070）

1 引言

半导体制造是现今最复杂的制造过程之一，具有多约束、可重入性、多目标、换模等特点，大多数半导体制造过程调度问题已被证明为NP-hard问题，因而给半导体晶圆制造系统建模和优化调度带来极大的复杂性，使其成为学术界的研究热点。

关于带换模约束调度问题前人有很多研究。Weng等［1］在调度问题中加入了关于工件加工顺序的换模，并以最小化总加权完成时间为目标，提出了一个有效的启发式算法。Arnaout等［2］针对换模时间与机器以及工件加工顺序有关的非等同平行机调度问题提出了两阶段蚁群优化算法，并与禁忌搜索算法等其他启发式算法对比，结果表明所提算法的有效性。Arnaout等［3］对上一篇文献所提做了改进，结果表明改进能够提高算法的绩效。Vallada和Ruiz［4］使用遗传算法来解决换模时间与机器以及工件加工顺序有关的非等同平行机调度问题，并与目前为止的最优方法进行比较，验证了遗传算法的有效性。Ying等［5］针对换模时间与机器以及工件加工顺序有关的调度问题提出了模拟退火算法，该算法运用了严格搜索策略以降低搜索难度，使算法能够更快地找到最优邻域。Fleszar等［6］将关于机器和工件顺序的换模加入到非等同平行机调度问题中，以最小化makespan为目标，运用基本蚁群算法（ant colony algorithm，ACO）对该调度问题进行求解。在Costa等［7］研究的非等同平行机调度问题中，换模时间也与工件加工顺序有关，并且同时考虑了进行换模操作的有限人力资源，其中，换模的时间与工人的操作熟练度有关，随后提出了三种遗传算法，实验结果表明混合遗传算法的效果最好。Wang等［8］研究了非等同平行机调度问题，该调度问题以最小化延迟工件数量和最大完工时间为目标，换模时间等约束都均与工件加工顺序相关，并且针对小规模问题提出了数学整数规划模型，针对大规模问题提出了一个指派规则。

上述文献在问题域方面主要考虑了基于工件加工顺序的换模约束、基于机器和工件加工顺序的换模约束、换模时间随着机器和工件加工顺序变化而变化等问题，有些还同时考虑了人力资源等。近年来，为了确保晶圆的加工质量，在实际生产中也会运用到参数调整。目前已有学者将参数调整作为一种特殊的换模考虑到调度问题中。Cai等［9］研究单机调度问题，在带有普通换模的多工件族单机调度问题的基础上，考虑了参数调整相关约束，并且提出了简单的启发式算法。

通过对上述研究现状分析可知，很多文献都没有考虑参数调整约束特征。且多以平行机为研究对象，在本文中，为了同时兼顾半导体晶圆制造的可重入性，将研究带有参数调整过程的可重入流水车间调度问题。

蚁群算法在车间调度问题中应用广泛［10～12］，但是容易陷入局部最优，为了提高蚁群算法的全局搜索能力，本文将分布估计算法［13～14］引入到蚁群算法中。

2 问题描述

在具有L个层次的J个步骤的可重入流水车间调度中，有来自I个工件族的工件待加工，工件族i中的工件加工时间是pi。若第l层的第j台机器，自从最后一次加工工件族i的工件，连续加工了ni个或者更多的不属于工件族i的工件，那么，在下一时刻在该台机器上加工工件族i时，必须先进行一次参数调整。在同一台机器上连续加工不同的工件时，需要进行换模操作。本文研究带换模约束的可重入流水车间调度问题，试图在参数调整次数与换模次数之间寻求一个均衡点，以实现系统最小makespan为调度目标。

本问题的假设如下：

1）来自同一工件族的工件之间不需要进行换模；

2）每次参数调整之前必须进行换模；

3）对于调度问题中的第一个工件，不管它属于哪一个工件族，都不需要进行参数调整，也就是说对于每种工件族在0时刻都有一个隐含的试运行；

4）工件加工没有优先级，即一旦工件的一个工序开始加工，则此工序不允许中断；

5）各个工序之间没有有限缓冲或者搬运时间；

6）一台机器在同一时刻至多只能加工一个工件，且一个工件在任意时刻至多只能在一台机器上加工。

3 数学模型

相关参数符号如下：

I为一组工件族，用i表示工件族序号；

L为一组待加工的层次，用l表示待加工层次序号；

J为一共有J个待加工步骤或机器，用j表示加工步骤序号；

为第l层的第j个步骤中一组调度的位置，用k表示调度位置的序号；如果工件族i的某一工件的第l层的第j个加工步骤在该层的该步骤中是第k个加工的，那么该工件在该层该步骤的位置用k表示；

pi为工件族i中的工件加工时间；

si为工件族i中的工件准备时间；

qi为工件族i进行参数调整需要的时间；

mi为工件族i所具有的工件数。

决策变量定义如下：

Ci，l，j表示工件族i在第l层的步骤j的完成时间。

根据上述问题描述、模型假设、参数以及决策变量，对所研究的带换模约束的可重入流水车间调度问题建模如下：

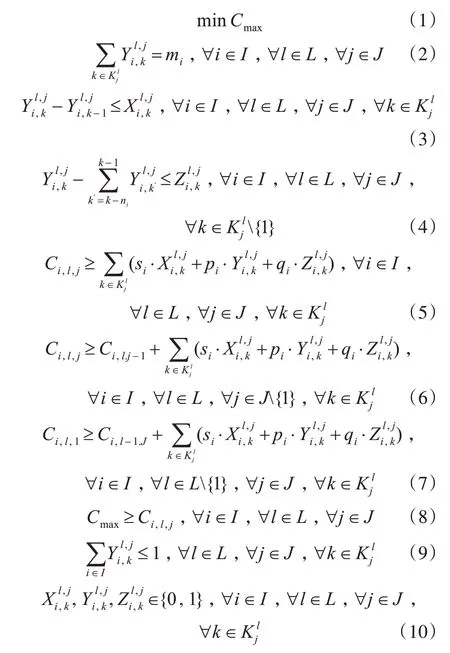
约束（2）表示每个工件族总的加工工件个数不超过每个工件族可加工的工件总数；约束（3）决定工件族i的第l层的步骤j上的k位置上是否需要执行换模过程。每台机器上的第一个工件在加工之前不需要换模，工件计数从0时刻开始，因此，设此外，任何具有负数标识的都设为0；约束（4）判断工件族i的第l层的步骤j上的k位置上加工之前是否需要进行参数调整。如果机器j在第k-ni到k-1这ni个位置上没有加工过与工件i同族的工件，那么机器j加工第k位置上的工件族i的工件之前需要进行参数调整方可加工该工件，否则可能导致产品出现质量问题，另外，在0时刻存在一个隐含的参数调整过程，所以约束（4）从k=2开始；约束（5）表明了加工族开始时间要求；约束（6）表明了工件族加工顺序要求，直到某个工件族的某一层的前一工序完成后，后一工序才能开始加工；约束（7）表明了工件族加工顺序要求，直到某个工件的某一层的最后一道工序完成后，后一层的第一道工序才能开始加工；约束（8）表明了Cmax的时间要求；约束（9）表明了每个位置至多只能有一个工件族可以加工；约束（10）表明了决策变量的范围。

4 算法构建

4.1 编码

4.1.1 节点

搜索空间中节点的构成如下：（a，pi，si，qi，ni，i，b），a表示工件族i中工件的序号，a∈[0，ci]，ci表示每个工件族中工件的个数，pi表示工件族的加工时间，si表示工件族的准备时间，qi表示工件族的参数调整时间，ni表示工件极限值，i表示工件族序号，I表示工件族数量，b表示节 点 编 号，，节 点 总 数 为，节点用πb=（a，pi，si，qi，ni，i，b）表示，节点集合为

4.1.2 路径

蚂蚁根据状态转移概率遍历搜索空间的所有节点，依次存入禁忌表Tabu中。可选节点集合Allowed=π-Tabu。禁忌表Tabu中所有节点构成了蚁群的一条运动路径，确定了各个层次各台机器上加工工件的顺序，也就是蚁群算法的一个解。在本问题中，有个节点需要被访问，假设已访问R-1个节点，则禁忌表表示在该台机器上已访问的节点集合，表示该台机器上总的可选节点，Allowed=π-Tabu表示当前第R个即将访问的节点的可选节点集合。

4.2 启发强度

首先引入如下记号：

m为蚁群中蚂蚁数量；

dxy为路径节点x和y之间的距离，反映由x到y的启发强度。

将m只蚂蚁随机放在m个节点上作为起点，每只蚂蚁以所在节点为中心，计算其他可选节点的可能性，可能性越大，该路径上的启发强度就越高。启发强度记为dxy由式（11）计算得出：

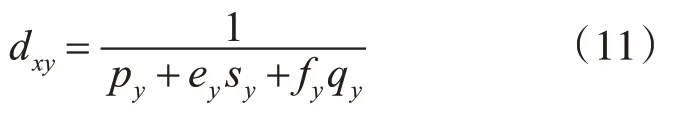
当节点y中的工件需要换模时，取ey=1，则d xy较小；否则ey=0。当节点y中机器最近加工的ni个工件都不来自节点y中的工件族i时，取fy=1，则dxy较小；否则fy=0。

4.3 状态转移规则与随机概率规则

蚂蚁k根据状态转移规则选择下一个要访问的节点y。状态转移规则为

其中，ηxs(t)和dxs(t)分别表示t时刻节点x和s之间的信息素强度和启发强度。α和β分别反映了蚂蚁运动过程中所积累的信息素和启发信息在选择路径中的相对重要性。

随机概率规则给出了蚂蚁k在t时刻位于节点x进行某次移动时选择前进到节点y的概率：

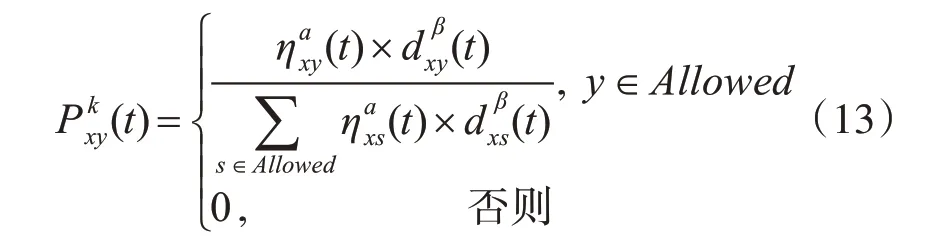
当(t)大于等于随机概率值时，蚂蚁选择节点y为下一前进方向。

为了改进现有蚁群算法容易陷入局部最优解的问题，把分布估计算法中的全局优化思想引入蚁群算法。首先在状态转移规则中考虑各个节点之间的概率分布因子对蚂蚁搜索的影响，则状态转移规则为

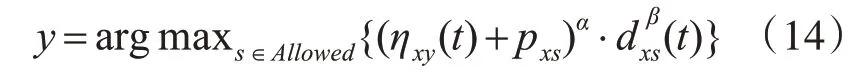
其中，pxs表示节点x与s之间被访问的次数。

随机概率规则为

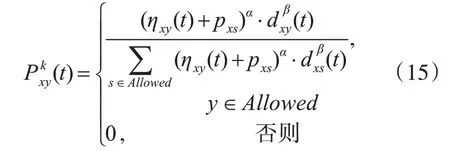
4.4 信息素的衰减与释放

信息素随着时间不断释放与衰减，释放主要源自于蚂蚁运动时在路径上留下的信息素的加强；衰减主要源于模拟生态的信息素挥发。具体根据式（16）调整［15］：

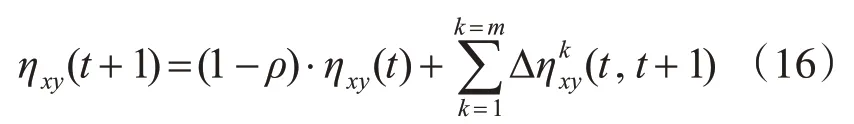
4.5 算法具体步骤

步骤1：初始化相关参数。

步骤2：将迭代次数t初始值设定为0。

步骤3：随机选择每只蚂蚁的初始节点。

步骤4：计算每只蚂蚁每个当前时刻的可选工序集以及对应启发强度，根据本文所提出的概率转移规则选择前进的节点，直到所有蚂蚁遍历所有节点。

步骤5：更新信息素。

步骤6：令t=t+1，如果达到最大迭代次数T则停止，否则转到步骤3。

5 仿真实验分析

5.1 参数设计

本实验结果通过makespan值和CPU时间来衡量，且设定最大迭代次数为100。

本实验测试了蚁群算法和所提出的混合蚁群分布估计算法（hybrid ant colony algorithm with esti⁃mation of distribution algorithm，ACO-EDA）求解各种不同规模的带换模和参数调整的可重入流水车间调度问题的性能。问题实例随机产生如下：I={3 ，5，7} ，M={4 ，6，8} ，J={3 ，4，5} ，L={1，2，3}；每种工件族的加工时间、换模时间和参数调整时间以及参数调整极限值分别由[45，65]，[5，10]，[45，65]，[3，5]离散均匀分布随机产生。I，M，J，L共有3×3×3×3=81种规模，对每种规模随机产生和测试10个不同的实例，故本实验共产生和使用810个测试实例。蚁群算法的参数设置：初始信息素量为5，蚂蚁数量为I*M，迭代次数T=100，α=2，β=5，γ=0.3。

本文算法采用以下计算机配置进行实现。CPU：英特尔奔腾双核T2130 1.86GHz；内存：896MB；电脑系统：Windows XPprofessional；编程语言：C++。

5.2 实验结果

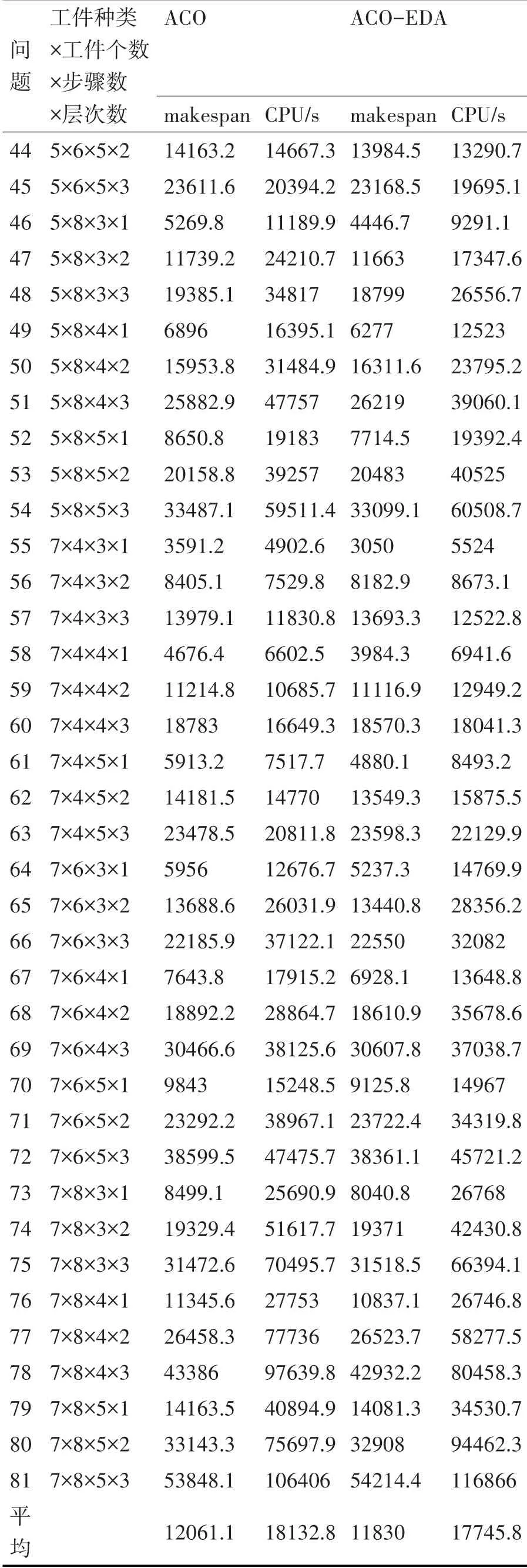
实验结果如表1所示，表1中的数据（除最后一行外）都是实验中相同规模的10个实例的平均性能。

从表1中可以看出，ACO和ACO-EDA在运行时间方面差不多，但是ACO-EDA几乎在各种规模均能比ACO产生更好的解，这是由于EDA考虑了全局信息，将全局信息融入ACO使得ACO-EDA在解的质量方面优于ACO。

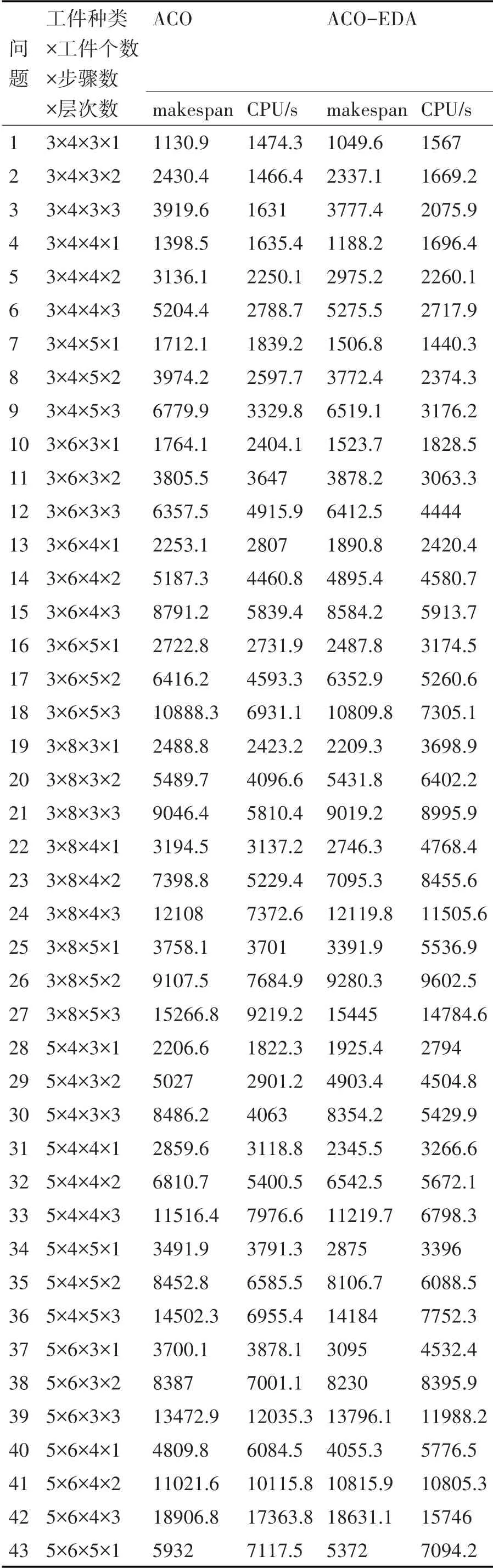
表1 不同规模问题的实验结果

44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81平均5×6×5×2 5×6×5×3 5×8×3×1 5×8×3×2 5×8×3×3 5×8×4×1 5×8×4×2 5×8×4×3 5×8×5×1 5×8×5×2 5×8×5×3 7×4×3×1 7×4×3×2 7×4×3×3 7×4×4×1 7×4×4×2 7×4×4×3 7×4×5×1 7×4×5×2 7×4×5×3 7×6×3×1 7×6×3×2 7×6×3×3 7×6×4×1 7×6×4×2 7×6×4×3 7×6×5×1 7×6×5×2 7×6×5×3 7×8×3×1 7×8×3×2 7×8×3×3 7×8×4×1 7×8×4×2 7×8×4×3 7×8×5×1 7×8×5×2 7×8×5×3 14163.2 23611.6 5269.8 11739.2 19385.1 6896 15953.8 25882.9 8650.8 20158.8 33487.1 3591.2 8405.1 13979.1 4676.4 11214.8 18783 5913.2 14181.5 23478.5 5956 13688.6 22185.9 7643.8 18892.2 30466.6 9843 23292.2 38599.5 8499.1 19329.4 31472.6 11345.6 26458.3 43386 14163.5 33143.3 53848.1 12061.1 14667.3 20394.2 11189.9 24210.7 34817 16395.1 31484.9 47757 19183 39257 59511.4 4902.6 7529.8 11830.8 6602.5 10685.7 16649.3 7517.7 14770 20811.8 12676.7 26031.9 37122.1 17915.2 28864.7 38125.6 15248.5 38967.1 47475.7 25690.9 51617.7 70495.7 27753 77736 97639.8 40894.9 75697.9 106406 18132.8 13984.5 23168.5 4446.7 11663 18799 6277 16311.6 26219 7714.5 20483 33099.1 3050 8182.9 13693.3 3984.3 11116.9 18570.3 4880.1 13549.3 23598.3 5237.3 13440.8 22550 6928.1 18610.9 30607.8 9125.8 23722.4 38361.1 8040.8 19371 31518.5 10837.1 26523.7 42932.2 14081.3 32908 54214.4 11830 13290.7 19695.1 9291.1 17347.6 26556.7 12523 23795.2 39060.1 19392.4 40525 60508.7 5524 8673.1 12522.8 6941.6 12949.2 18041.3 8493.2 15875.5 22129.9 14769.9 28356.2 32082 13648.8 35678.6 37038.7 14967 34319.8 45721.2 26768 42430.8 66394.1 26746.8 58277.5 80458.3 34530.7 94462.3 116866 17745.8问题工件种类×工件个数×步骤数×层次数ACO makespan CPU/s ACO-EDA makespan CPU/s

图1、2、3分别描述了两个算法在I=3，I=5，I=7时的270个问题的平均进化曲线。纵轴表示每个算法的270个例子的平均makespan值。从各图中均可以看出，两种算法的初始解十分接近，然而不同之处在于，ACO收敛速度更快，ACO-EDA虽然收敛速度不如ACO，但是最终解的质量优于ACO。这是由于ACO虽然收敛速度快，但是容易陷入局部最优，而ACO-EDA考虑了全局信息，从而进行全局优化。

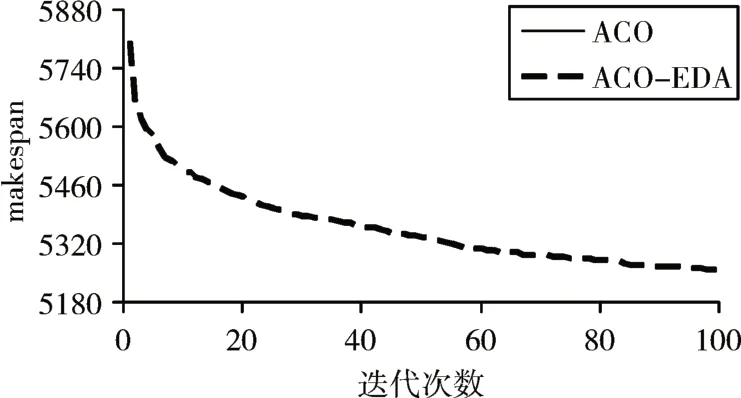
图1 I=3时的进化曲线

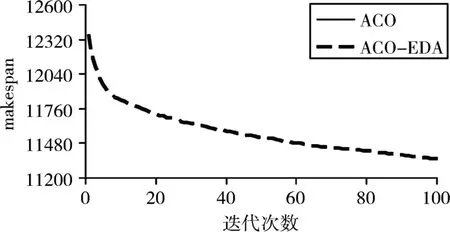
图2 I=5时的进化曲线

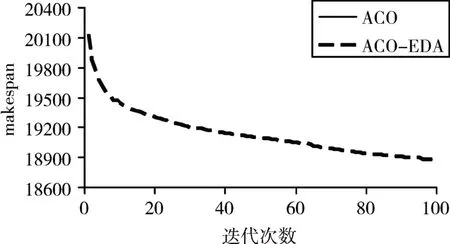
图3 I=7时的进化曲线

6 结语

本文对带换模约束的可重入流水车间问题进行了研究，提出了混合蚁群分布估计算法，将分布估计算法引入到蚁群算法中。首先对该问题进行了问题描述，并以系统makespan最小化为目标建立数学规划模型，随后对蚁群算法进行了针对本问题的编码设计和启发强度设计，并将分布估计算法引入到蚁群算法中，提高了蚁群算法的全局搜索能力。最后实验结果证明混合蚁群分布估计算法在运行时间差不多的情况下，几乎在各种规模下均能比蚁群算法产生更好的解，说明了引入分布估计算法的有效性。