基于语言直觉模糊集的应急物流预案决策
2021-06-01刘利枚龚尹励曹文治
刘利枚,龚尹励,曹文治,杨 艺+
(1.湖南工商大学 大数据与互联网创新研究院,湖南 长沙 410205;2.湖南工商大学 新零售虚拟现实技术湖南省重点实验室,湖南 长沙 410205)
0 引言
突发事件要求决策者需在短时间内制定应对策略,完善而有效的应急预案可为决策者在时间紧迫的情况下制定有效的处置措施并提供有力的帮助。为确保理想地处置突发事件,尽可能将突发事件所造成的损失降到最低,对应急预案的有效性进行预先评估十分必要。应急物流管理是突发事件应急管理的重要研究内容之一,加强应急物流预案决策问题研究,有助于完善和改进应急物流体系。应急物流预案决策模型可以有效判定预案的关键内容与薄弱环节,基于决策模型的应急物流决策研究对提升应急物流管理水平和决策水平具有重要意义。
在应急预案决策过程中,由于应急问题具有复杂性和模糊性,决策者较难提供精确数值形式的预案评价值,通常采用语言术语信息[1]作为评价值,如“差”、“一般”或“好”等。近年来,随着模糊集理论的快速发展和应用,语言术语集和模糊集融合衍生了一系列模糊语言术语集,如犹豫模糊语言术语集[2]、比率犹豫模糊语言术语集[3]、概率犹豫模糊语言术语集[4]、语言直觉模糊术语集[5]、语言区间直觉模糊术语集[6]等。相比定量数据分析决策方法[7-9],基于定性语言术语集构建的多属性决策方法的灵活性和适用性更强,相关决策方法被用于解决各领域的多属性决策问题[10-21]。在应急预案决策方面,基于直觉模糊集和语言术语评价信息的转换关系,Chen等[12]构建了直觉模糊应急预案决策方法;通过利用语言术语信息测度应急预案属性之间的支持度,Xiong等[13]提出考虑属性关联的民航应急预案决策方法;Wu等[14]建立了基于概率犹豫模糊语言偏好关系和信任推荐机制的应急决策模型,以解决H7N9流感病毒应急预案决策问题;Zhou等[15]将构建的概率犹豫模糊语言术语应急决策方法用于解决地震应急救援方案决策问题;Xu等[16]构建了基于广义非对称语言偏好关系的大型群体应急决策方法,通过火灾爆炸事故算例分析表明方法的合理性;尹念红等[17]提出基于多粒度语言信息表征的公共工程突发事件应急决策方法;李磊等[18]提出基于信息公理和多粒度语言值的铁路应急预案评估方法;张倩生等19]构建了基于相对信息熵和语言加权算子的网络舆情突发事件群决策模型;Zhang等[20]提出基于模糊语言术语信息粒度的群共识应急决策模型,用于解决液氨泄漏应急决策问题;常建鹏等[21]提出基于犹豫模糊语言术语集的铁路应急预案群决策模型。
上述研究表明,应急决策偏好的表征形式由定量信息向定性的语言术语信息发展,相关的语言模糊应急决策方法已经在地震、火灾、航空、医疗、公共工程、铁路运输、网络舆情、化学事故等突发事件应急问题中得到应用。然而,在突发事件应急物流预案决策研究中,基于语言术语信息表征的群决策方法研究较少。基于上述分析,本文拟引入由定性语言术语集和区间直觉模糊集相结合所形成的语言区间直觉模糊集[6],提出用于集结语言区间直觉模糊数组的集结算子,构建专家客观权重模型,并构造基于字典序关系的逼近理想解法(Technique for Order Preference by Similarity to Ideal Solution,TOPSIS),进而构建应急物流预案群决策方法,以增强应急预案决策的科学化水平。
1 理论基础
本章主要对语言区间直觉模糊集的相关概念进行回顾,为后续的研究内容奠定基础。
定义1[1]设S={sθ|θ=0,1,…,h},其中h为正整数,sθ为一个语言变量的可能取值,且满足:①若θ>δ,则sθ>sδ;②存在补算子neg使得neg(sθ)=sh-θ。则称S为离散的语言集。
例如,h=8时的语言集S={sθ|θ=0,1,…,h}={极差,很差,差,略差,一般,略好,好,很好,极好}。为方便语言之间的计算,文献[22]将离散的语言集拓展成连续的语言集S[0,h]={sθ|θ∈[0,h]}。
定义2[23]设X为给定的集合,则X上的直觉模糊集
I={〈xi,uI(xi),vI(xi)〉|xi∈X}。
(1)
式中uI(xi)和vI(xi)分别表示元素xi属于集合I的隶属度和非隶属度。二元组(uI(xi),vI(xi))被称为直觉模糊数(Intuitionistic Fuzzy Number, IFN),方便起见,将直觉模糊数简记为β=(uI,vI),uI,vI∈[0,1],uI+vI≤1。
定义3[3]设X为给定的集合,则X上的语言直觉模糊集为
A={(x,suA(x),svA(x))|x∈X}。
(2)
式中:suA(x)∈S[0,h]为语言隶属度,svA(x)∈S[0,h]为语言非隶属度。对于任意x∈X,uA+vA≤h。二元组(suA(x),svA(x))被称为一个语言直觉模糊数,简记为α=(suA,svA),suA,svA∈S[0,h],u+v≤h。若suA,svA∈S,则称α为原始的语言直觉模糊数,否则称为虚拟的语言直觉模糊数。

(3)
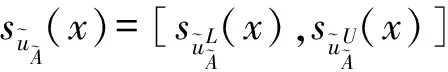
文献[6]定义了LIVIFNs之间的4种运算法则,下面将已有的4种运算法则通过T-模和S-模的方式给出,具体如下:

[sh·TA(c1/h,c2/h),sh·TA(d1/h,d2/h)]);
[sh·SA(c1/h,c2/h),sh·SA(d1/h,d2/h)]);
式中:SA和TA分别为单位区间上的代数(Algebraic)S-模和T-模,满足SA(x,y)=1-(1-x)(1-y);TA(x,y)=xy,fA:[0,1]→[0,∞]和gA:[0,1]→[0,∞]分别为SA和TA的生成元,满足fA(x)=-ln(1-x),gA(x)=f(N(x)),N为单位区间上的标准否定函数,且满足N(x)=1-x。

(1)语言区间直觉模糊加权平均算子定义为
(4)
(2)语言区间直觉模糊加权几何算子定义为
(5)

(6)


2 应急物流预案群决策模型的构建
语言区间直觉模糊集是语言术语集与区间直觉模糊集的融合形式,其不仅能够通过定性表征的方式呈现评估对预案的偏好,还能从隶属度、非隶属度和犹豫度3个维度全面直观表征评估者偏好的不确定性。基于此,本文建立基于语言区间直觉模糊偏好表征的应急物流预案决策评估方法,该方法的核心内容包括提出语言区间直觉模糊集结算子、构造专家权重优化模型,以及在语言区间直觉模糊环境下拓展TOPSIS方法。
2.1 应急物流预案群决策问题描述与预案的评价指标体系
为方便表述,用以下符号描述应急预案决策问题中涉及的相关集合与变量:

(2)预案集X={x1,…,xm}为m个候选的应急物流预案集合,其中xi∈X表示第i个应急物流预案,i=1,2,…,m;C={c1,…,cn}为针对应急预案的n个评估指标的集合,其中cj∈C表示第j个指标,j=1,2,…,n。
根据应急物流预案评价指标体系的构建思路和原则,以及国内外应急预案和相关领域的研究成果,郭子雪[24]构建了应急物流预案评价指标体系,如表1所示。

表1 应急物流预案评价指标体系[24]
2.2 指标评估值的集结
2.2.1 现有算子的不足
目前,已有的语言区间直觉模糊集结算子主要包括定义6中的LIVIFWA算子和LIVIFWG算子,两类算子基于AlgebraicS-模和T-模构建,下面通过例子和定理分析两类算子的不足。

(1)通过定义5中的运算法则可得:
[s10×(4/10)0.6,s10×(4/10)0.6])=([s3.402,s3.402],
[s5.771,s5.771]);
[s10×(2/10)0.6,s10×(2/10)0.6])=([s1.927,s1.927],
[s3.807,s3.807])。

由例1可知现有运算法则和算子存在如下不足:


针对算子失效现象,有如下定理:

(7)
(8)
文献[25]通过例子揭示了基于Algebraic T-模和S-模定义的直觉模糊运算和算子的缺点,并引入ukasiewiczT-模和S-模[26]定义了直觉模糊集的运算法则和算子,ukasiewicz运算和算子能够有效克服Algebraic运算和算子的不足。本文为克服LIVIFWA算子和LIVIFWG算子的不足,引入ukasiewicz T-模和S-模,定义语言区间直觉模糊集的ukasiewicz运算法则和集结算子。

其中SL和TL分别为单位区间上的ukasiewicz S-模和T-模,满足SA(x,y)=min{1,x+y},TA(x,y)=max{0,x+y-1},fA(x)=x和gA(x)=1-x分别为SA和TA的生成元。

(9)

(10)


(11)

(12)

证明幂等性显然成立,下面证明(2)和(3)。根据定义7和定理2可得:








上述分析表明,L-LIVIFWA算子可以有效克服LIVIFWA算子和LIVIFWG算子的不足。因此,本文将利用L-LIVIFWA算子对专家组的个体评价矩阵进行集结,在集结个体矩阵之前,需要获取专家组的权重向量。
2.3 专家权重的确定
专家权重的确定方法主要有客观赋权法、主观赋权法和主客观组合法。在群体决策过程中,某个个体与综合评价结果偏差越大,其偏离群体的共同意愿越远,相应地赋予专家较小的权重,从而减弱该专家对群体一致性的影响;反之,偏差越小,越能代表群体意愿,其决策意见的力度也应该越大,则相应地赋予该专家较大的权重。本文提出一种主观权重和客观权重联合赋权的方法。
λk∈λ,k=1,2,…,t。
(13)
式中θ为重要度因子,满足0≤θ≤1,对于所有k=1,2,…,t,重要度因子具有如下特点:


为给专家分配合理的权重,构建基于群体共识测度的权重优化模型。
下面提出语言区间直觉模糊数之间的距离测度,并定义个体矩阵与综合矩阵之间的距离测度,进而构建基于群体共识测度的专家客观权重优化模型。

(14)


(15)

定义12应急物流预案群决策中的群体共识测度定义为
Con=1-maxkd(Dk,D)。
(16)

群体共识衡量专家之间达成协议的最终决定水平,群体共识越高,一致性越高,决策结果越可靠。因此,通过最大化群体一致性,建立一个优化模型来获取专家的权重,模型M1如下:
maxCon=1-maxkd(Dk,D)。

(17)
根据定义10,模型M1可以转换为模型M2:
s.t.
0≤θ-≤θ≤θ+≤1;
i=1,2,…,m,j=1,2,…,n,k=1,2,…,t。

2.4 基于字典序关系的语言区间直觉模糊TOPSIS方法
TOPSIS[27]首先明确正、负理想评估值,然后确定候选预案的评估值与正、负理想评估值的距离,越靠近正理想值的同时越远离负理想值的预案为最佳预案。然而,根据当前语言区间直觉模糊集的排序方法,会出现无法确定正、负理想评估值的情形,为此提出一种基于字典序法的语言区间直觉模糊TOPSIS方法。

=([saij,sbij],[scij,sdij])
(18)
首先,介绍语言区间直觉模糊TOPSIS方法的3个核心阶段:

i=1,2,…,m,j=1,2,…,n。
(19)


(20)

(3)计算方案xi(i=1,2,…,m)的贴近度
(21)
贴进度COi越大,相应预案xi(i=1,2,…,m)的实际表现越优;反之,贴进度COi越小,预案xi(i=1,2,…,m)越差。
不难发现,在阶段(1)中,语言区间直觉模糊数的排序方法扮演着重要的角色,其作用在于锁定正理想值和负理想值。然而,由例3可见定义7排序方法的局限性。

Farhadinia[28]将字典序方法拓展到犹豫模糊环境下,基于记分函数构建了犹豫模糊字典序方法,用于犹豫模糊数的排序;Beliakov等[25]提出区间模糊数的波动函数(或称区间长度),进而基于区间中心和波动函数定义了区间模糊的排序方法。在此基础上,为了克服定义7中排序方法的局限,本文提出语言区间直觉模糊数的波动函数,引入字典序的概念,构建了语言区间直觉模糊字典序关系。


(22)

(23)
式中:Unc([sa,sb])=b-a为隶属度波动函数;Unc([sc,sd])=d-c为非隶属度波动函数。
定义14[29]设X=(x1,…,xn)∈n和Y=(y1,…,yn)∈n为实数域上的两个数组,欧几里得空间上的字典序关系(记为 X=(x1,…,xn) (24) 当且仅当存在1≤i≤n,使得xj=yj对j (25) 基于排序向量,定义语言区间直觉模糊数的字典序关系。 上述结果表明,语言区间直觉模糊字典序方法可以有效克服定义7中排序方法的局限性。下面描述L-LIVIFWA算子与字典序关系的单调性。 (26) 综上可知,语言区间直觉模糊字典序关系具有良好的性质,其不仅能够高效区分和锁定各指标下的正负理想值,还能使L-LIVIFWA算子满足单调性。 基于前面所提集结算子、专家权重优化模型和TOPSIS方法,构建应急物流预案群决策方法,主要步骤如下: 步骤2执行2.3节中的权重优化模型,求解专家的综合权重向量λ*=(λ1,…,λt)T。 步骤4执行语言区间直觉模糊TOPSIS方法,获取方案的贴近度。 步骤5根据贴近度的值获取方案xi(i=1,2,…,m)的排序。 本节构建的应急物流预案群决策方法主要由语言区间直觉模糊集结算子、基于群共识度的专家权重模型、语言区间直觉模糊数的排序方法3部分构成,从评价信息的合理融合、群体共识度的最大化、相异模糊数的区分3方面突出决策方法的特点。 本章采用所构建的群体决策方法解决森林火灾事故的应急决策问题,以验证所提方法的合理性和有效性,并通过对比分析现有算子表明本文方法的科学性。 表2 专家评价矩阵 采用本文所提方法获取最优应急物流预案,具体步骤如下: 步骤2基于表2中的评价信息及专家的主观权重向量,假设预设的参数范围为0.5<θ≤1,将上述信息带入模型M2,通过Lingo软件求解模型,获取客观权重向量λobj=(0.20,0.48,0.32)T、综合权重向量λ=(0.39,0.36,0.25)T和最优参数θ*=0.59。 表3 基于L-LIVIFWA算子获取的综合评价矩阵 续表3 步骤4执行TOPSIS方法: (3)计算方案xi的贴近度: CO1=0.835,CO2=0.249, CO3=0.613,CO4=0.484。 步骤5根据贴近度的值获取方案xi(i=1,2,3,4)的排序x1≻x3≻x4≻x2,最优预案为x1。 例5分别应用文献[6]提出的两类算子(LIVIFWA/LIVIFWG算子)和本研究所提出的L-LIVIFWA算子对属性评价信息进行集结,并对比通过这些算子所获取的应急物流预案决策结果。 表4 评价信息及决策结果 根据表4可得: 例5的结果表明,当应急群决策过程中出现极端评价信息干扰时,文献[6]中的两类算子无法获取合理的决策结果,相比之下,L-LIVIFWA算子能够有效克服极端值的干扰,从而获取较为科学的决策结果。 本文基于语言区间直觉模糊偏好表征的应急物流预案群决策方法主要从集结评价信息算子、优化专家权重的共识模型、综合评价信息的排序3方面展开研究。 (1)信息集结 已有的语言区间直觉模糊集结算子在遭遇极端信息时,会产生集结结果失效的现象,并失去算子关于排序关系单调的性质,这些不足大大提高了决策失误发生的可能性。算例表明L-LIVIFWA算子能有效克服算子失效现象,并满足序关系的单调性,合理集结专家的个体评价矩阵。 (2)专家权重 群体共识度低会影响群体决策结果的可靠性。以距离测度为工具的群体共识测度能够衡量个体与群体之间的一致性,以群共识最大化为目标的优化模型能够合理获取专家的客观权重,综合权重的重要度因子使决策者能够较灵活地调整主客观之间的侧重比例。 (3)综合评价信息排序 在针对不同语言区间直觉模糊数进行排序时,如果这些模糊数的隶属度区间中心和非隶属度区间中心均相同,则基于记分函数和精确度函数的排序方法无法对这些模糊数实施排序。字典序关系的提出有效解决了该问题,增强了TOPSIS中正负理想值的区分性能。 本文虽然通过L-LIVIFWA算子和共识测度对应急物流预案的信息集结、专家权重建模进行了分析,并构建了有效的决策模型,但是在现实情况下,应急物流预案的指标之间可能存在关联性,本文只考虑了属性之间相互独立的情况,因此,未来可以在此基础上对该问题进行深入研究,进一步考虑预案指标之间关联下的应急物流预案决策。










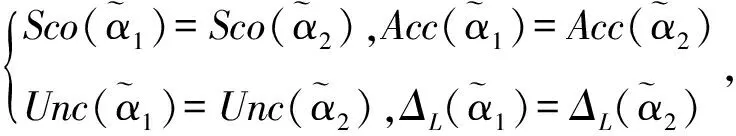


2.5 应急物流预案群决策方法


3 算例分析与对比分析
3.1 算例分析








3.2 对比分析






4 结束语
