基于犹豫模糊DEMATEL与风险屋的供应链风险管理
2021-06-01何丽娜王国涛
何丽娜,王国涛,刘 珏
(西南交通大学 机械工程学院,四川 成都 611730)
0 引言
在全球市场下,各企业的社会分工越来越具体,产品生产从原材料到用户消费形成一条完整的供应链。然而,由于不确定性因素的影响以及供应链成员之间的密切联系,一个或多个风险因素可能破坏整个供应链的正常运行,因此有必要对供应链风险及其处理方式进行深入研究。
供应链风险管理的目的是采取有效的风险处理方式,最大限度地降低风险造成的影响,然而不同的风险处理方式消耗的成本不同,对风险的处理效率也不同。因此,在资源有限的情况下,识别出关键风险处理方式对企业高效开展风险管理具有重要的意义[1]。由于风险处理方式是为解决风险事件,风险事件因风险因素的存在而发生,建立合理的模型分析这三者之间的映射关系,并将风险因素的信息传递给风险处理方式,是供应链风险管理的关键问题之一。
风险因素是风险处理方式的驱动因素,而且各风险因素间存在互相影响,准确识别风险因素的重要度是供应链风险管理的基础。Chopra等[2]指出已经确定的供应链风险与其他风险之间的关系会形成新的潜在风险,从而对供应链造成危害。因此,对供应链风险因素之间关联关系的识别和分析是供应链风险管理中的第二大问题。
为分析供应链风险因素之间的关联关系,袁悦[3]采用模糊层次分析法评估阿里巴巴并购饿了么的风险。层次分析法可以使系统变量之间的关系简洁化,但其定量数据较少,定性成分较多,不易令人信服;决策与试验评价实验室(DEcision—MAking and Trial Evaluation Laboratory, DEMATEL)方法通过系统中各要素之间的逻辑关系和直接影响矩阵,可以计算出每个要素对其他要素的影响度和被影响度[4]。Song等[5]采用粗糙DEMATEL方法分析持续性供应链风险,但缺乏对犹豫度的考虑。
供应链风险管理过程中涉及较多主观评价信息,现有研究一般采用模糊理论处理评价中的主观性。王浩伦等[6]采用三角模糊软集处理基于失效模式和后果分析(Failure Mode and Effect Analysis, FMEA)的风险管理中的模糊信息;胡辉等[7]提出区间直觉模糊理论,在直觉模糊集中加入了非隶属度的概念,并应用区间数表达区间模糊信息,然而这些模糊信息处理方式难以处理元素隶属度为多个取值的情况[8];Torra[9]提出的犹豫模糊集方法允许元素的隶属度有多个选值,可以解决这一问题;耿秀丽等[8]基于犹豫模糊集改进FMEA风险评估,表明采用犹豫模糊语义术语集合更符合专家的决策偏好。
基于以上分析,本文将犹豫模糊集与DEMATEL、风险屋(House of Risk, HoR)进行集成,构建了犹豫模糊DEMATEL-HoR模型。首先,采用犹豫模糊DEMATEL分析风险因素之间的关联关系,并确定风险因素的重要度;然后构建多阶段犹豫模糊HoR模型,分析风险因素与风险事件、风险事件与风险处理方式之间的关联关系,从而将风险因素的重要度逐步传递到风险事件、风险处理方式中,最终确定风险处理方式的优先度,为供应链风险管理提供有效的决策依据,以便公司更加快捷合理地配置资源。
1 基于犹豫模糊集的群评价语义量化
1.1 犹豫模糊集的定义和量化
定义1[9]假设对某项评价对象的所有可能评价语义组成一个集合L,则有L={li|i=1,2,…,n},其中li是语义的第i个等级程度。设某专家对该项评价的犹豫语义为RL,则RL是L的一个有序子集,即RL∈L。
二元语义网络是一种有效的语义词计算方法,可以将语义术语转化为数字,对语义数据进行计算,从而将二元语义网络广泛应用于专家系统和模糊逻辑控制等领域[10]。
设λ∈[0,n]为一个数字集,令i=round(λ),i∈[0,n]。为了量化犹豫语义,引入函数Δ使数字集与语义集一一对应[11]:
Δ[0,n]→L×[0.5,-0.5);
Δ(λ)=(li,αi)。
(1)
式中:i=round(λ),li=round(λ),αi=λ-i,αi∈[0.5,-0.5),round为取整算子,α为符号转移值。
反之,反函数Δ-1将一个语义转化为对应的数值:
Δ-1:L×[0.5,-0.5)→[0,n];
Δ-1(li,αi)=i+αi=λ。
(2)
1.2 基于粗糙集的群评价信息处理
为了方便计算比较语义,应用粗糙集处理量化后的语义信息。粗糙集采用区间及上下近似的方法进行信息处理,无需提供问题所需处理的数据集合之外的任何先验信息,因此对问题不确定性的描述或处理比较客观。
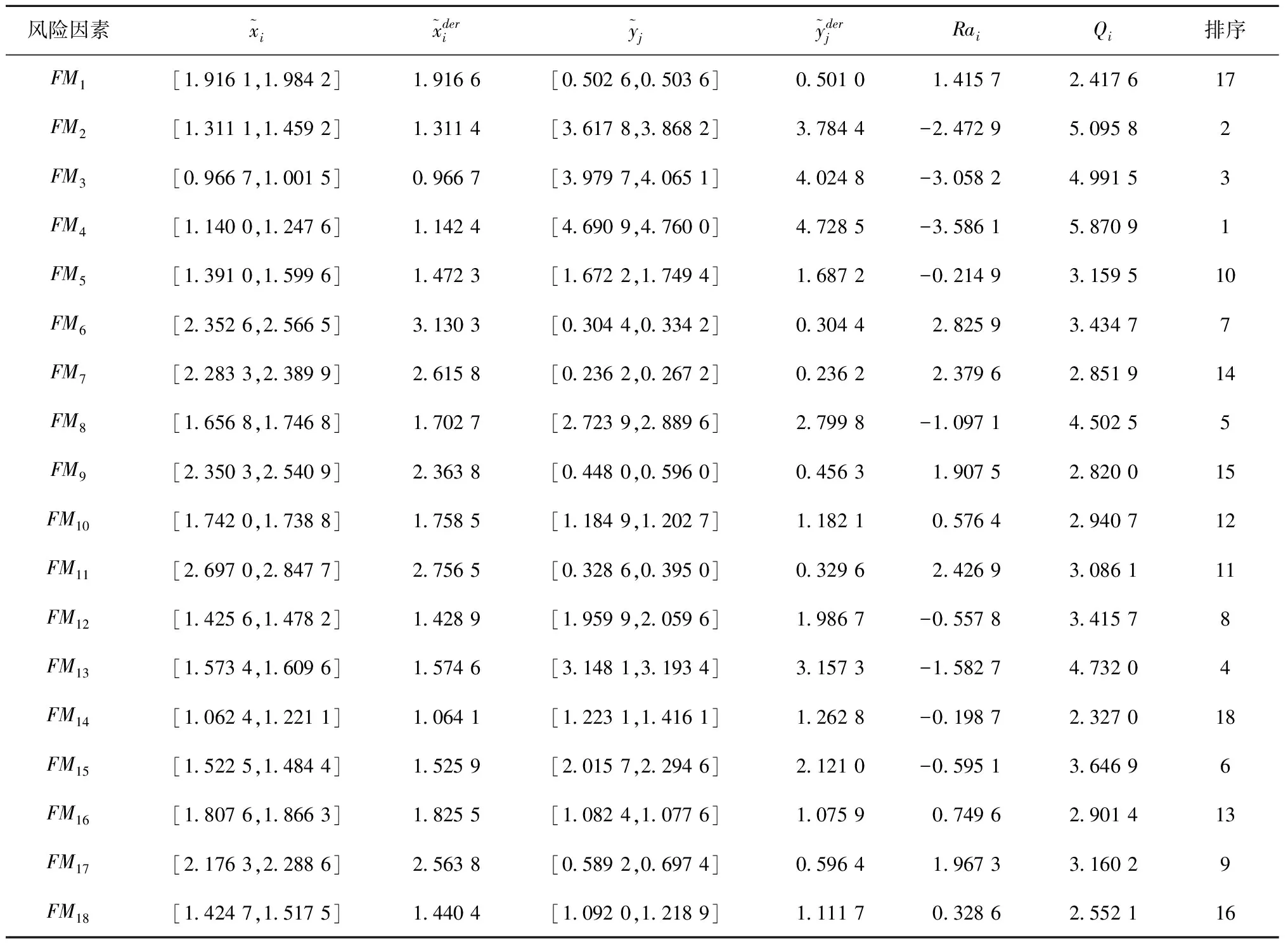
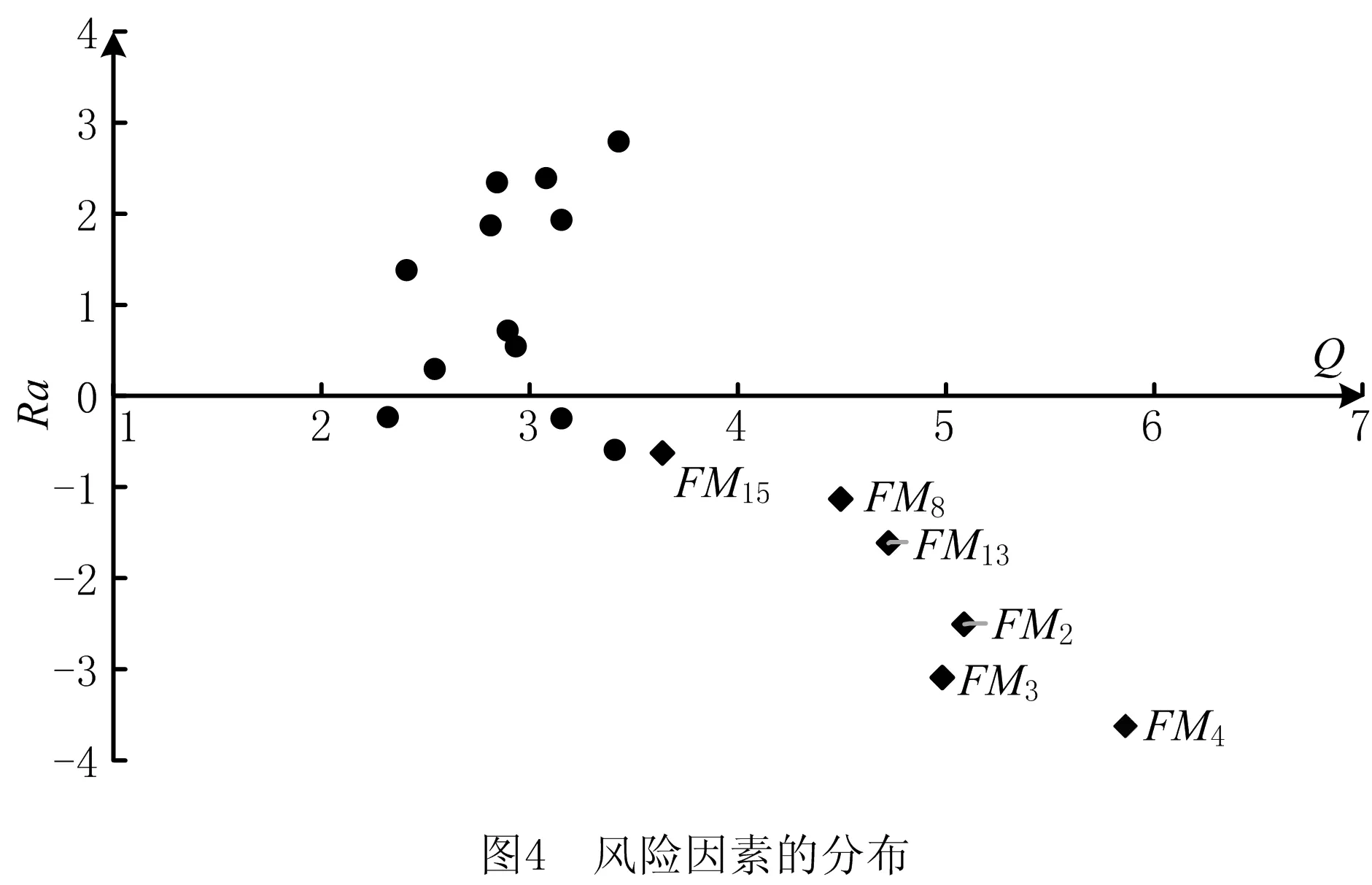
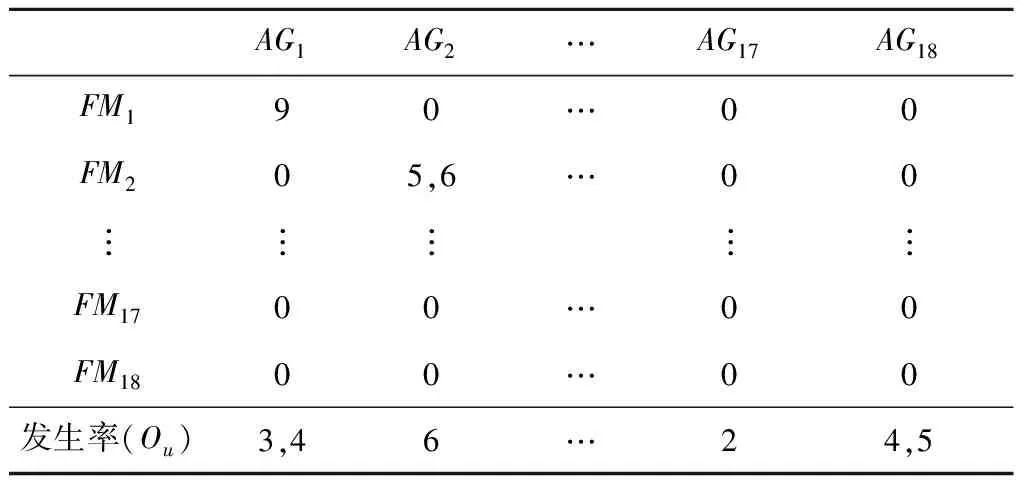
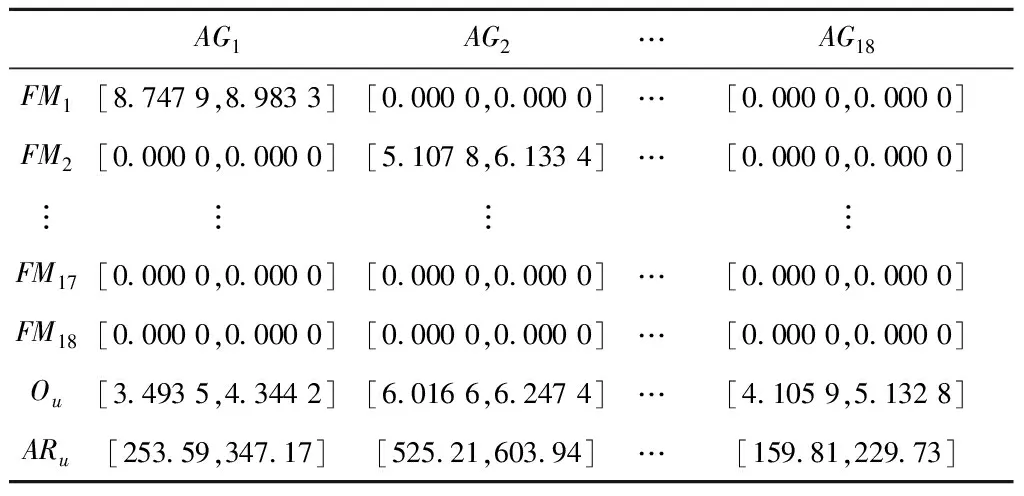
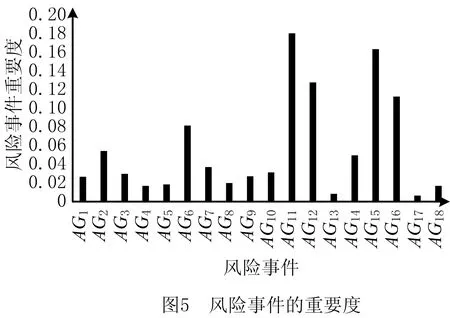
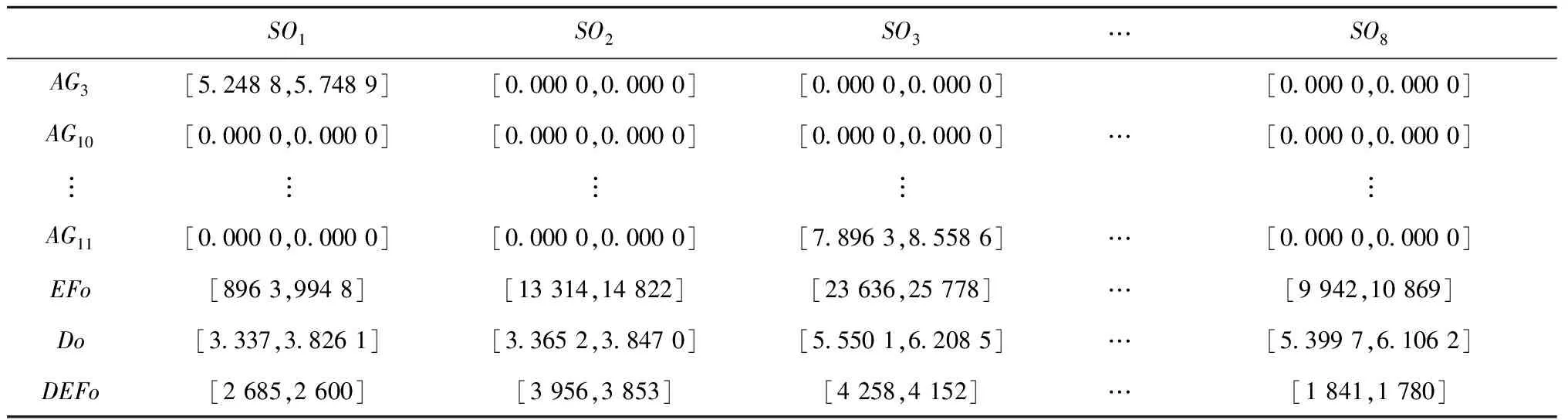
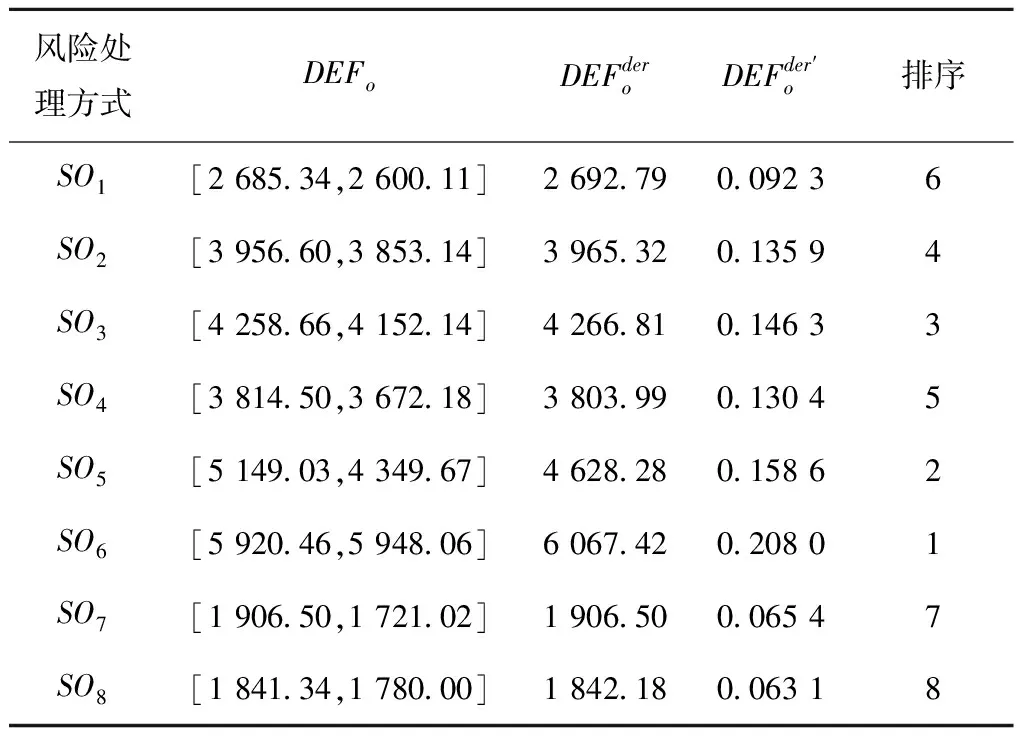
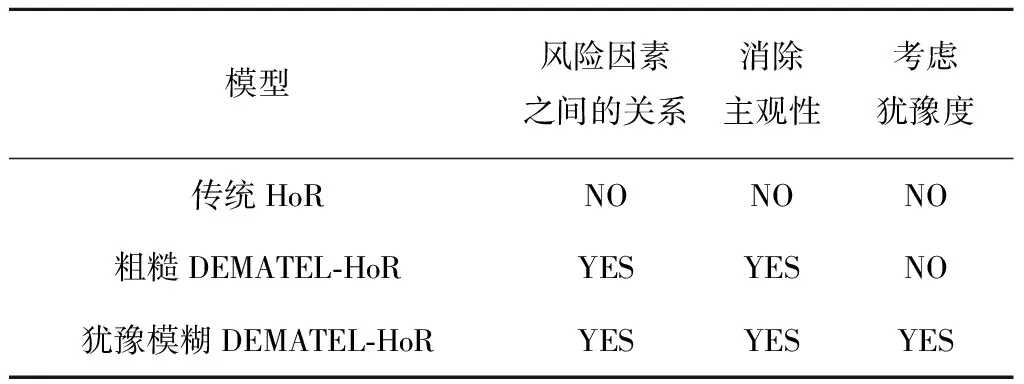
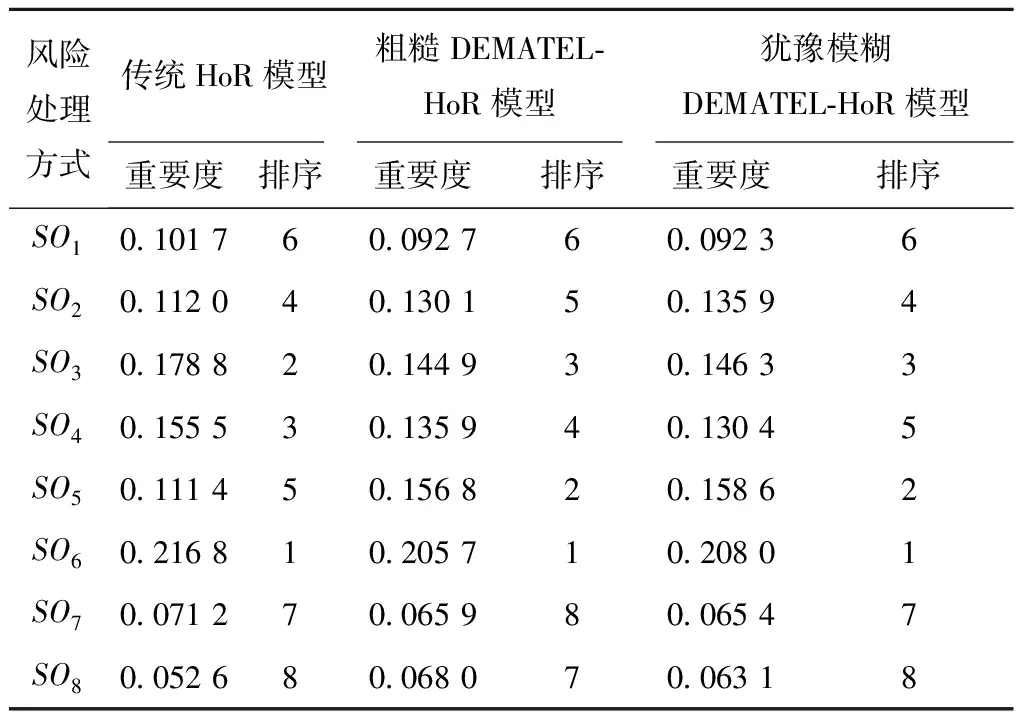
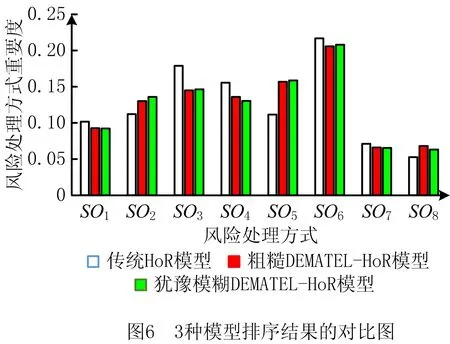
定义2[12]假设集合U是评价信息表中所有对象组成的论域,共分为m个类,m个类组成集合J,J={e1,e2,…,em},且存在e1 定义元素ek的下近似域为 (3) 元素ek的上近似域为 (4) (5) 式中:xi和yi分别为上下近似域中的元素;NU和NL分别为上下近似域中的元素总数。 根据式(3)~式(5),J中的所有元素可以转化为粗糙数 采用粗糙集的方式对量化的语义Δ-1RL(υi)进行处理,将Δ-1(RL(υi))={l1,…,ln}转化为粗糙数集合,然后用式(6)得到该语义的粗糙区间数 (6) 假设ωk为第k个专家的权重,采用式(7)对某项评价对象的群评价信息进行集成: (7) 采用犹豫模糊DEMATEL的方法分析风险因素之间的关联关系,并确定其重要度,具体步骤如下: 步骤1构造并量化风险因素的直接关联矩阵。 假设有m个风险因素,集合为{FMi|i=1,2,…,m},其中FMi表示第i项风险因素。有n位专家,其权重集合为{ωk|k=1,2,…,n},第k位专家应用表1中的语义集1和语义集2分别评估m个风险因素的重要度以及风险因素之间的关联程度,得到风险因素直接关联矩阵 表1 评价语义集 Δ-1(Rk)= 用式(7)对群评价信息进行处理,得到供应链风险因素的群评价直接关联矩阵 步骤2直接关联矩阵的归一化。 以矩阵各行向量元素之和的最大值为标准对直接关联矩阵R进行归一化: (8) (9) 步骤3计算综合影响矩阵。 将归一化后的直接关联矩阵N按照上下限分解为 (10) (11) 步骤4计算综合影响矩阵T的行粗糙数和列粗糙数。 综合影响矩阵T的行粗糙数 (12) 综合影响矩阵T的列粗糙数 (13) 步骤5粗糙数精确化。 为了准确直观地对风险因素的重要度进行对比,将粗糙数转化为精确数,具体步骤如下[5]: (1)归一化处理 (14) 按式(15)计算修正值 (15) (16) 步骤6计算风险因素的重要度。 假设风险因素重要度的向量集为Q,则有 (17) 另外,根据风险因素FMi的影响度及被影响度的差值Rai,可将风险因素分为两类。其中 (18) 当Rai为正数时,FMi为原因型因素;当Rai为负数时,FMi为结果型因素。 质量屋(House of Quality, HoQ)是一种直观的矩阵框架表达形式,其通过定量分析实现输入信息到输出信息的转换。基于HoQ理论,根据风险因素、风险事件、风险处理方式之间的关系,本文提出犹豫模糊HoR模型,从而实现风险因素到风险处理方式的信息转换和传递,如图1所示,其中风险因素集为{FMi|i=1,2,…,m}、风险事件集为{AGu|u=1,2,…,ag}、风险处理方式集为{SOo|o=1,2,…,so}。 由专家应用表1中的语义集2对风险因素和风险事件的关联关系进行评价,构建一阶段犹豫模糊HoR模型,如图2所示。 图中Ciu表示风险事件AGu与风险因素FMi之间的相关程度;Ou表示风险事件AGu的发生率,由专家用表1中的语义集3做出判断。 用式(1)~式(7)对一阶段犹豫模糊HoR中的Ou和Ciu分别进行二元语义转化和粗糙化处理,得到相应的粗糙数,其中 令风险事件AGu的重要度为ARu[1], (19) 然后,对风险事件重要度进行归一化: (20) 根据风险事件和风险处理方式之间的关联关系,构建二阶段犹豫模糊HoR模型,如图3所示。 图中Euo表示风险处理方式SOo与风险事件AGu的关联程度,由专家采用表1中的语义集2表达;Do表示第SOo项风险处理方式的实施难度,由专家利用表1中的语义集4针对风险处理方式所耗费的资源和时间进行评价。 用式(1)~式(7)对Euo和Do分别进行二元语义转化、粗糙化处理,得到相应的粗糙数形式,其中 令EFo为风险处理方式SOo的初始重要度, (21) 对于风险处理方式SOo,若其实施难度Do较小,则应赋予较高重要度。应用Do对风险处理方式SOo的初始重要度EFo进行修正,以确定最终重要度DEFo, (22) (23) 某印度尼西亚大型国有肥料公司共有3个生产工厂,主要生产各种肥料,包括尿素、重过磷酸钙(Triple Super Phosphate, TSP)、有机肥料等。该工厂生产的主要原料为天然气及各种化学试剂,如硫、氯化钾等。下面以该公司的供应链风险分析为例验证本文所提方法的有效性。 5名供应链风险管理专家根据公司的历史供应链风险管理资料、专业知识和经验对供应链的风险因素、风险事件进行分析评价,最终确定的主要风险因素和风险事件如表2所示。 表2 风险因素与风险事件项目表 续表2 5位专家的评价权重分别为{ω1=0.3,ω2=0.2,ω3=0.2,ω4=0.2,ω5=0.1}。各个专家分别使用语义集1、语义集2评价风险因素的重要度及其之间的关联联系,从而得到直接关联矩阵Rk。用式(1)和式(2)对语义进行量化,第1位专家的评价结果如表3所示。 表3 专家1的直接关联矩阵 用式(3)~式(6)对评价信息进行粗糙处理,用式(7)得到风险因素直接关联矩阵的群评价矩阵R,如表4所示。 表4 风险因素的群评价直接关联矩阵 用式(8)和式(9)对群评价矩阵R进行归一化处理,得到矩阵N,然后根据式(10)和式(11)得到综合影响矩阵T,如表5所示。 表5 风险因素的综合影响矩阵 表6 风险因素的重要度 以Qi为横坐标,Rai为纵坐标,绘制风险因素的分布图,如图4所示。图中位于纵轴上半轴的因素为原因型因素,位于纵轴下半轴的风险因素为结果型因素,前6项关键风险因素用菱形标记。 从图4可见,风险因素的重要度排序为FM4>FM2>FM3>FM13>…>FM1>FM14,最重要的风险因素是FM4(没有具体的采购规格),且为结果型因素,易受其他因素的影响;FM6(自然灾害)为原因型因素,容易影响其他因素。 4.3.1 一阶段风险屋 5位专家分别采用语义集2、语义集3评价风险事件发生的频率、风险因素与风险事件之间的关联程度。例如:专家1对需求大幅增大(FM1)和原材料不足(AG11)的评价为联系紧密,用式(1)和式(2)对语义进行量化,则专家1所构建的一阶段HoR如表7所示。 表7 专家1构建的一阶段HoR模型 用式(3)~式(6)对表7中的数据进行粗糙处理,然后用式(19)计算风险事件的重要度,如表8所示。用式(14)~式(16)可得风险事件重要度的精确数,并用式(20)进行归一化处理,分析结果如表9和图5所示。 表8 一阶段粗糙HoR模型 表9 风险事件的重要度和排序 由图5可见,各风险事件之间的重要度差异较大,其重要度排序为AG11>AG15>AG12>…>AG13>AG17,其中最关键的风险事件为AG11(原材料不足),其次是AG15(配送中心产品短缺)。 4.3.2 二阶段风险屋 由于各风险事件重要度存在差异,公司应该集中资源解决重要风险事件,针对前10项风险事件开展风险处理。经过5位专家的研究和分析,共列出8项风险处理方式(如表10),并采用语义集2、语义集4分别评价风险事件与风险处理方式之间的关联度,以及风险处理方式的执行难度,从而构建二阶段HoR。采用式(1)~式(6)对相关评价信息进行量化并进行粗糙处理,如表11所示。 表10 风险处理方式 表11 二阶段粗糙HoR模型 用式(21)和式(22)依次计算风险处理方式的初始重要和最终重要度,如表11所示。用式(14)~式(16)将粗糙数转化为精确数,并用式(20)进行归一化处理,结果如表12所示。则风险处理方式的重要度排序为SO6>SO5>SO3>SO2>SO4>SO1>SO7>SO8。其中最关键的风险处理方式为SO6(与运输公司更好地协助),其次是SO5(授权企业资源计划(Enterprise Resource Planning, ERP)系统)等。从结果可以看出,虽然SO6比SO5实施难度更高,占有的资源更多,但是SO6比SO5的排序靠前,部分原因是SO6比SO5更能解决一些关键风险事件。 表12 风险处理方式的重要度及排序 为了验证犹豫模糊DEMATEL-HoR集成模型的有效性,本文将传统HoR模型、粗糙DEMATEL-HoR模型与本文方法进行对比,3种方法在风险因素相关性、模糊信息处理上存在差异,如表13所示。 表13 不同研究模型的对比 分别应用传统HoR模型、粗糙DEMATEL-HoR模型对本案例中的风险因素、风险事件和风险处理方式进行分析,结果如表14和图6所示。 表14 3种模型的排序结果 在传统HoR模型中,SO5(授权ERP系统)与SO3(与实力强大的供应商合作)和SO4(引进先进库存管理方法)的排序发生了变化,其原因主要是传统HoR模型没有考虑风险因素之间的关系,导致风险因素的重要度分析不全面。另外,传统HoR模型缺乏对模糊信息的处理,也会出现分析结果不一致的情况。 从图6可见,粗糙DEMATEL-HoR模型与犹豫模糊DEMATEL-HoR模型的结果相差不大。在粗糙DEMATEL-HoR模型下,SO2(改善员工工作环境)和SO4(引进先进库存管理方法)的排序发生了变化,原因主要是粗糙DEMATEL-HoR模型缺乏对犹豫度的考虑。 综上所述,犹豫模糊DEMATEL-HoR集成模型一方面可全面分析风险因素之间的关联关系,另一方面可有效、准确处理风险管理中的模糊信息,为开展供应链风险管理提供了系统化的决策依据。 针对现有供应链风险管理方法的不足,本文从模糊信息处理、供应链风险之间的关联关系,以及供应链风险与风险事件、风险处理方式之间的转换关系出发,提出基于犹豫模糊DEMATEL与HoR集成模型的供应链风险管理方法,其主要特点如下:①采用基于粗糙思想的犹豫模糊集群评价方法可合理表达专家的评价犹豫度,并解决模糊集隶属函数主观性强的问题;②基于犹豫模糊DEMATEL可有效分析风险因素之间的相互关系,并确定其重要度;③采用犹豫模糊HoR模型实现风险因素、风险事件及风险事件处理方式之间的系统化映射,并将风险因素的重要度传递到风险事件处理方式中,从而确定风险事件处理方式的排序。最后,通过案例分析及对比验证了所提方法能够为供应链风险管理提供更全面、有效的决策依据。 然而,本文涉及较多的主观评价,且未考虑历史数据对供应链风险管理的作用,后续研究将关注数据驱动的供应链风险管理。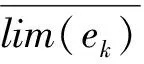
2 基于犹豫模糊DEMATEL的供应链风险因素重要度分析
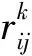

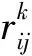
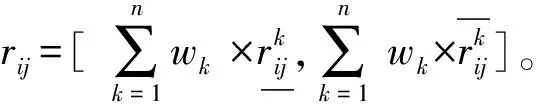
3 基于犹豫模糊风险屋模型的风险处理方式重要度分析
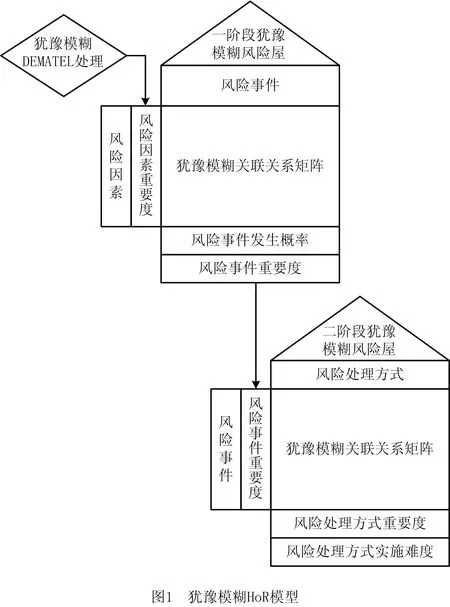
3.1 一阶段犹豫模糊风险屋模型
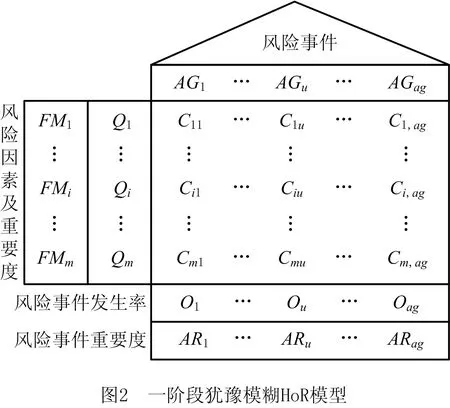
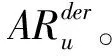
3.2 二阶段犹豫模糊风险屋模型
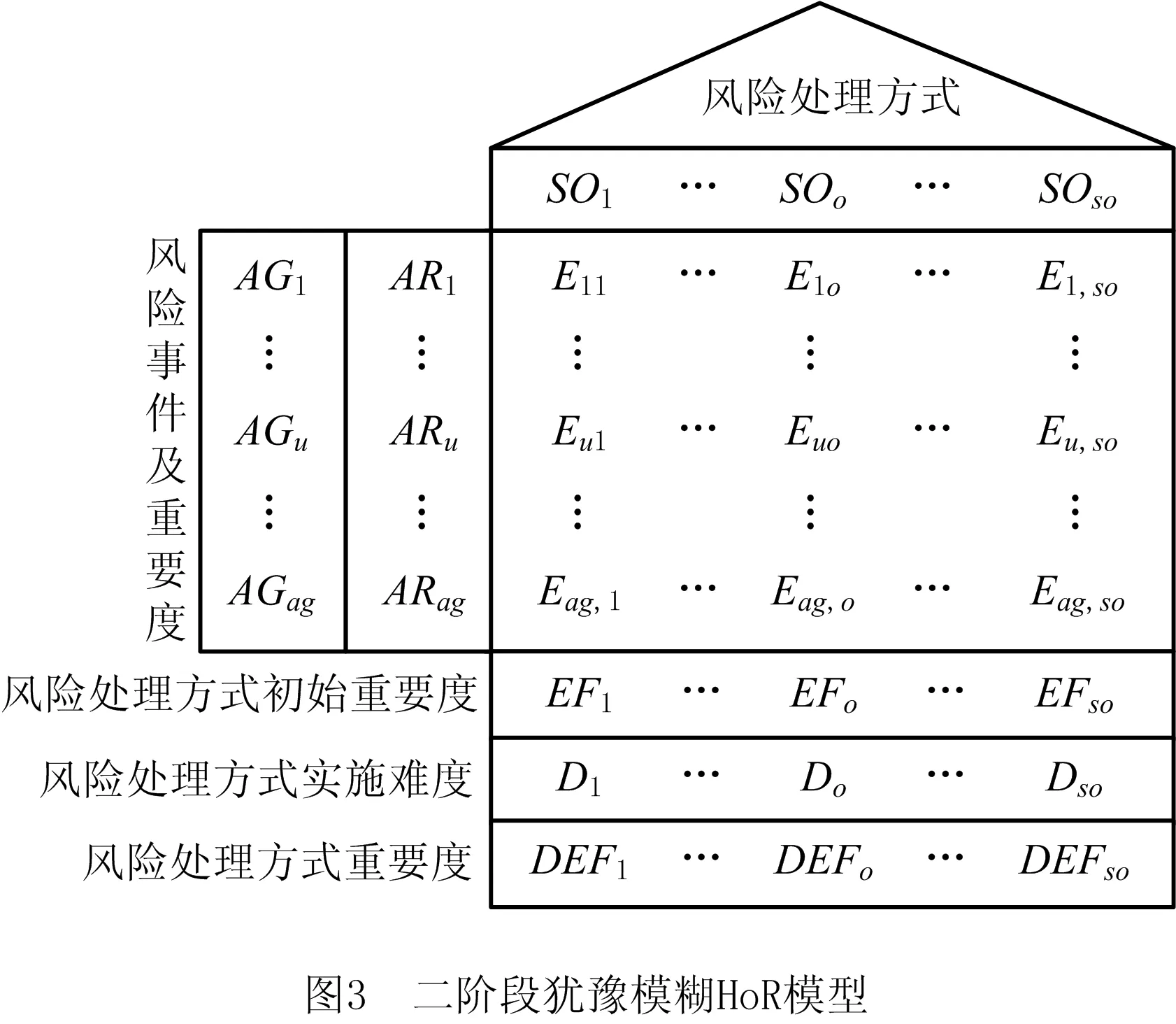
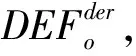
4 案例分析
4.1 风险识别


4.2 风险评估
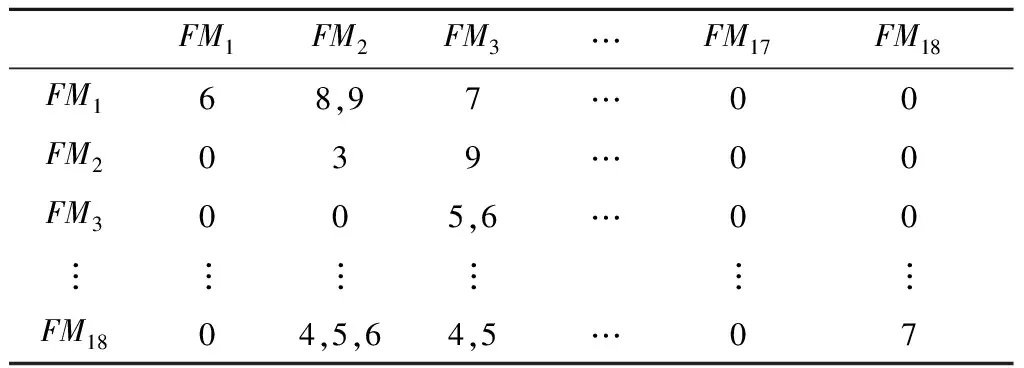
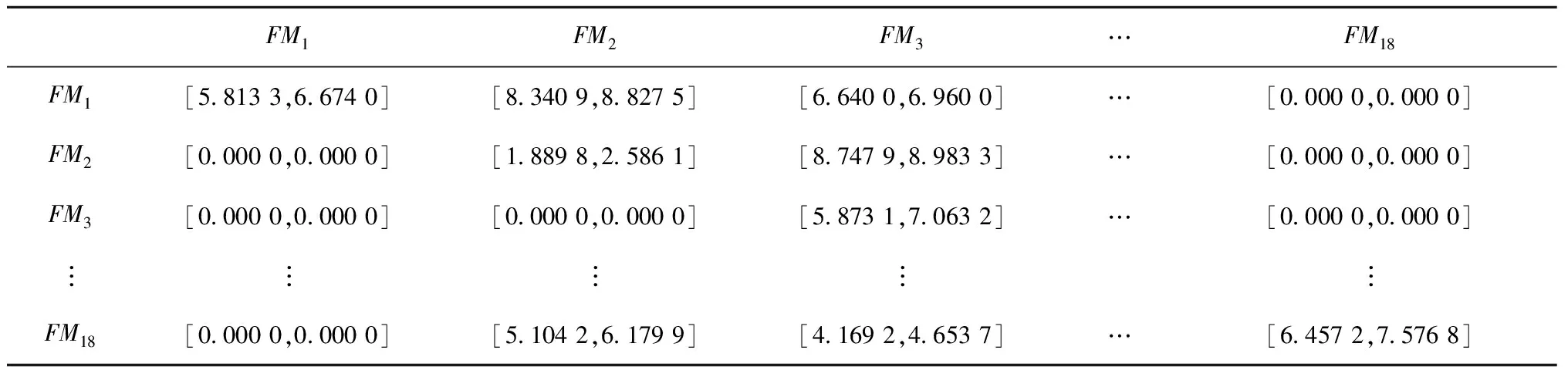
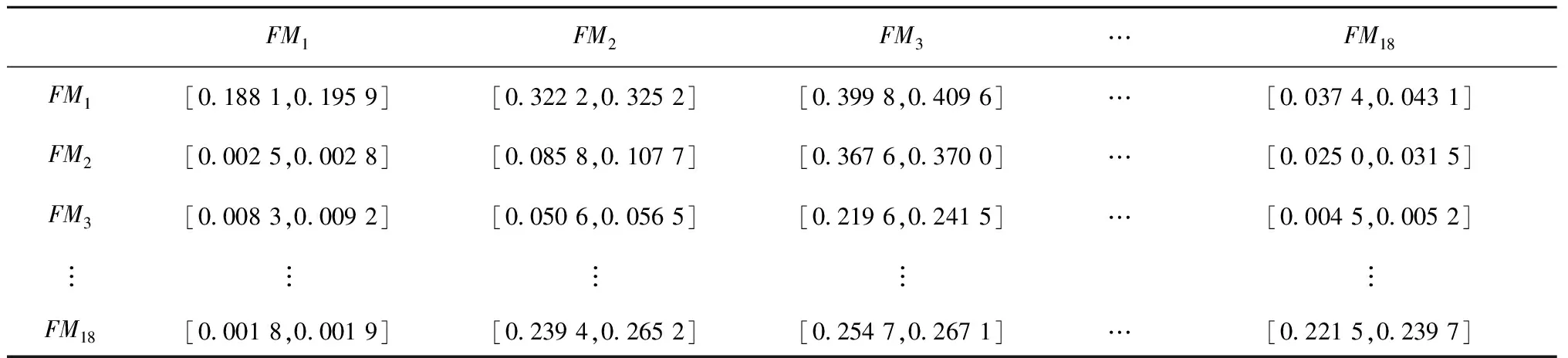
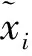
4.3 风险处理方式重要度计算


5 方法比较分析
6 结束语
