下穿隧道对邻近桩基承载力与沉降的影响

王超雄，胡裕琛，莫品强，高新慰

(1. 中冶集团武汉勘察研究院有限公司，湖北 武汉 430080; 2. 中国矿业大学 深部岩土力学与地下工程国家重点实验室，江苏 徐州 221116； 3. 中国矿业大学 力学与土木工程学院，江苏 徐州 221116)

0 引 言

进入21世纪以来，中国进入城市化建设的快车道，城市化进程不断加快，城市规模不断扩大，造成市政工程管道不断修建、城市绿化面积减少、交通堵塞、空间拥挤等“城市综合症”。为解决这一问题，中国城市发展需向三维立体式发展。城市隧道和地下综合管廊的开发利用是作为解决“城市综合症”和实现城市可持续发展的有效手段[1]，但由于城市空间的限制和修建数量的增长，不可避免地涉及到“穿越工程”和“近接工程”。隧道和综合管廊施工通常采用暗挖法，开挖会涉及到土体原位应力的卸载释放问题[2]，造成原有的土体应力平衡状态破坏，导致土体应力重分布和新的沉降变形，对周围环境产生破坏。城市中心区域的建筑物通常采用桩基础承担上部荷载，开挖造成的应力扰动必然会破坏桩-土之间的平衡，对桩基的稳定性和安全性产生消极影响。

隧道开挖对桩基影响的工程问题起始于20世纪70年代，之后研究较少，由于目前中国大力兴建地下隧道，此工程问题逐渐突出。本文通过整理前人的传统研究成果及小孔扩张-收缩理论研究现状，分析现有结果的优点和缺点，提出应用有限介质小孔扩张-收缩理论在浅埋隧道开挖对桩基影响的前景，为之后的研究提供参考。

1 隧道-桩基相互作用的分析方法

隧道开挖施工过程中不可避免地会对周围地层产生扰动，破坏桩-土之间原有的应力平衡。隧道开挖使单桩桩基附加位移，使群桩桩基产生非均匀沉降，这会对建筑物的使用产生影响。目前对于该问题的研究方法可分为两阶段分析法、整体分析法和室内模型试验3种方法。

1.1 两阶段分析法

两阶段分析法是隧道-桩基相互作用问题中应用最为广泛的求解方法。该方法将计算过程分为2个阶段。在阶段一通过经验总结或理论计算得到隧道开挖时造成的无桩位置处土体沉降位移，在阶段二将阶段一得到的位移附加至桩身部分，建立相应的力学模型得出桩基的力学行为反应。

在第一阶段中隧道开挖引起的土体位移求解方法主要为经验法和理论计算，主要成果如表1所示。在阶段一中的经验总结主要为Peck[3]通过对大量的工程案例实测数据进行统计分析，拟合出地表沉降计算公式。在此过程中Peck首次提出“地表沉降槽”的概念，分析地层位移是由于隧道开挖形成的地层损失引起。之后Jacobsz等[4]归纳总结大量的室内离心试验，得出地表沉降槽的范围是Peck曲线分布的1.5倍，因此对Peck公式进行了修正。在阶段一的理论计算方面，将土体假设为半无限空间弹性体进行求解。Loganathan等[5]提出“等效地层损失”的概念，求解出不排水条件下盾构隧道施工引起的土体自由位移场。Verruijt等[6]提出任意泊松比下均质半无限弹性空间中土体位移场的解析解。

表1 隧道开挖引起土体位移的经验公式与理论解析Tab.1 Empirical Formula and Theoretical Analysis of Soil Displacement Caused by Tunnel Excavation

阶段二的求解是将阶段一求解得到的土体自由位移场转化为附加应力施加于桩身，求解过程为将桩基等效为一根地基梁，将桩基分为n个点，采用麦克劳伦方程和有限差分法求解，常用的力学模型有Winkler地基模型、Pasternak地基模型、Kerr地基模型和边界元软件等。图1为模型示意图。

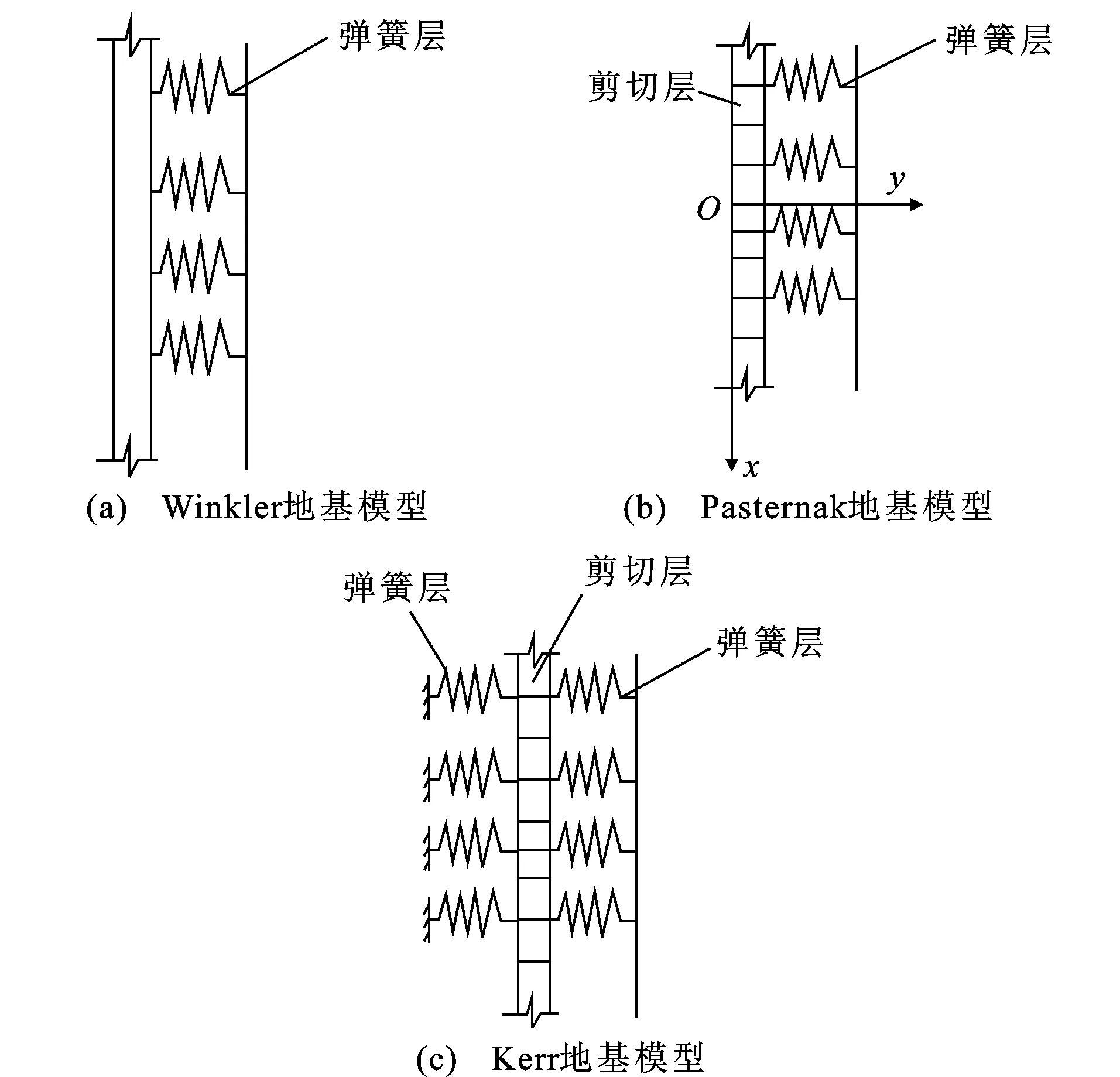
图1 隧道-桩基相互作用时的地基模型Fig.1 Foundation Models Considering Interaction Between Tunnel and Pile Foundation

Loganathan等[7]在阶段二采用边界元程序GEPAN进行计算，将阶段一求解的土体自由位移场附加至桩身，得到隧道开挖对群桩的影响。黄茂松等[8]在阶段二采用Winkler地基模型得到隧道开挖对群桩的轴力。张治国等[9-10]在阶段二采用Pas-ternak地基模型，得到了隧道开挖对单桩水平位移的影响，并采用Kerr地基模型分析了弹簧参数和剪切层厚度对单桩水平位移的影响。

两阶段分析法通过将隧道-桩基之间相互作用简化分为2个阶段，得到隧道开挖对桩基的水平位移、轴力、弯矩等力学反应，计算简便而被广泛使用。隧道-桩基相互作用是一个复杂的三维动态问题，此方法的假设是在二维平面内进行求解，对于隧道掘进过程中桩基的动态反映难以求解，不能完全反映隧道-桩基相互作用问题。

1.2 整体分析法

计算机技术的进步推动了求解岩土工程问题的进程。通过计算机的计算能力将隧道和桩基视为一个整体进行分析。该方法的整体思想是化整为零，集零为整。通过将物体切分为有限个单元，采用变分原理和加权余量法进行求解，之后将得到的单元解积分为整体的求解结果。与两阶段分析法相比，整体分析法可以将隧道-桩基相互作用作为一个整体考虑，整体的结果较为合理。

朱逢斌等[11]根据苏州轻轨穿越桩基的实际工程，采用ABAQUS有限元软件建立了三维有限元数值模型，讨论了不同竖向集中荷载作用下，盾构隧道开挖引起的承载基桩中水平位移和桩身轴力的力学反应。郭孝坤[12]用三维有限元研究了隧道下穿单桩桩基过程中桩基不同弹性模量、桩长、桩身上部荷载对桩身沉降和轴力的影响。韩进宝等[13]运用位移控制法对邻近桩基受隧道开挖影响进行了三维有限元数值模拟分析。图2为隧道开挖的变形模型，其中g0为隧道收缩的间隙参数。采用PLAXIS有限元软件进行分析，并与试验结果对比。结果表明：相同位置处的桩身轴力和弯矩随着桩长与隧道埋深比Lp/Htun的增大而增大，但Lp/Htun>1时，桩身轴力的趋势呈现先增大后减小；Lp/Htun>1.2时，桩身的弯矩值几乎不变。分析了桩长与隧道的埋深比受隧道-桩基水平距离、地层损失比、土体固结桩基内力和变形、弯矩的影响。

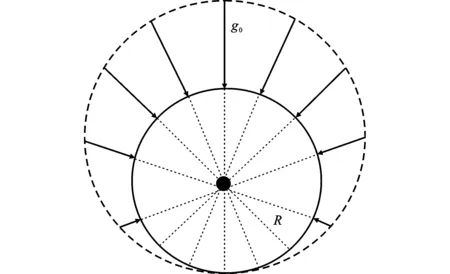
图2 隧道开挖的变形模型Fig.2 Deformation Model of Tunnel Excavation

1.3 室内模型试验

在隧道开挖穿越桩基的实际工程案例中，由于桩基已经埋入土体使用，在桩身上安装测试元件较为困难，大多学者开始进行室内模型试验，根据相似原理将隧道穿越桩基工程采用离心机手段进行缩减，在模型桩上贴测试元件获取数据。Jacobsz等[4]通过离心机模型试验模拟在密实干砂土体中隧道开挖对挤土桩的影响，利用模型中水的体积模拟隧道的地层损失，并研究了不同隧道-桩基间距下桩基的力学反应，给出了位于土体不同区域的桩基所受到的影响。A，B，C区域将会发生大变形，其中A区域为桩基沉降最严重的区域，D区域为土体的弹性小变形，如图3所示，φ为土体内摩擦角。

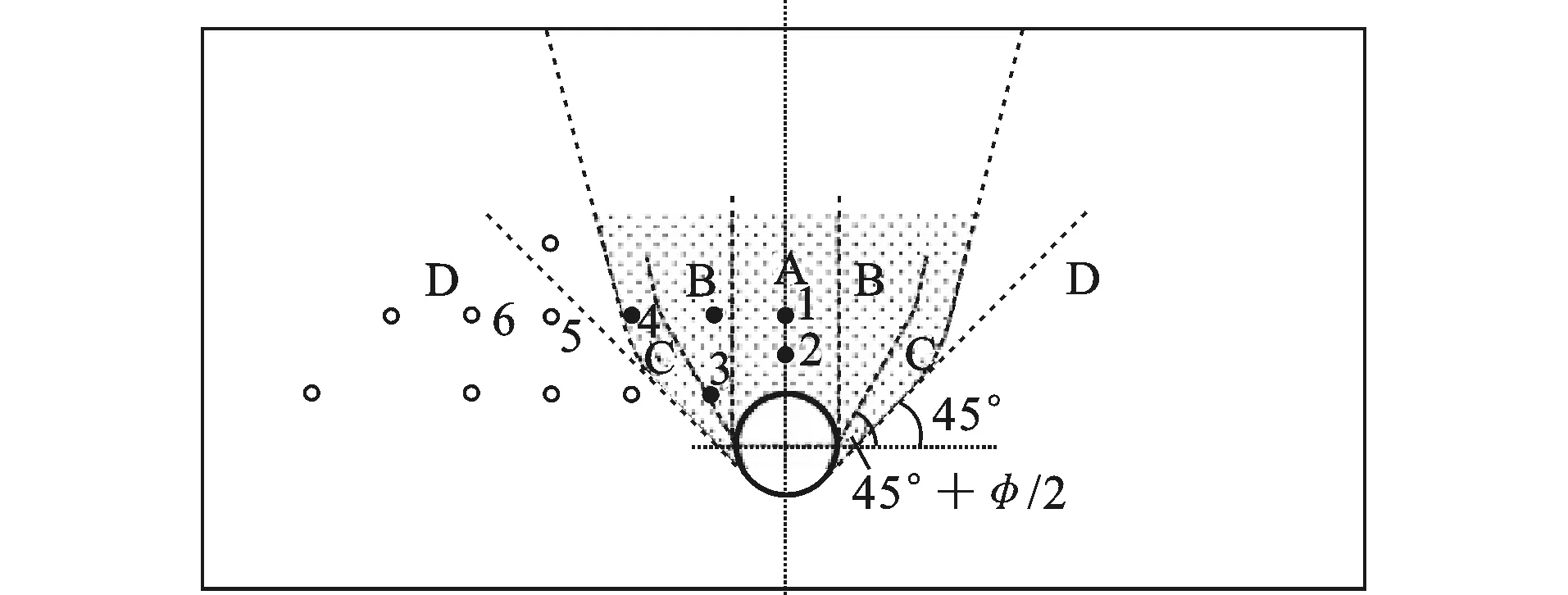
图3 隧道开挖对土体沉降的影响区域Fig.3 Influence Zones for Tunnelling-induced Soil Settlement

Lee[14]等采用离心机研究了饱和砂土中隧道开挖引起的桩基影响，并对在不同工况下邻近隧道开挖的单桩响应进行研究。试验得到了桩身轴力和弯矩沿着桩身长度的分布，当地层损失比为3%～3.5%时，桩身的轴力和弯矩明显增大。隧道浅埋开挖时，桩端产生的正弯矩和负弯矩大致相同，但当隧道深埋开挖时，桩端产生的负弯矩较大；当隧道-桩基间距较小时，桩身在不同深度处的单位摩阻力大小取决于桩身的法向应力和桩土之间的相对位移。

Marshall[15]通过离心模型试验研究了隧道开挖对挤土桩的影响。试验主要分为2个阶段，阶段一先将桩基打入土体形成挤土桩后在桩基上部增加荷载，使得土体原来的应力场发生改变，在此基础上，将隧道进行开挖，得出桩基的承载力衰减系数、沉降位移及周围土体的应力场和位移场。在地层损失比为0.5%～1%时，桩基沉降主要发生在隧道正上方的土体区域，当地层损失比为1.75%时，将会对桩基产生影响，桩端部分土体持力层将会发生应力重分布，桩基开始产生沉降，承载力降低，当地层损失比增加至5%时，桩基产生大变形，承载力有较大损失。

孙庆等[16]采用离心机试验研究了隧道开挖在黏土中引起的沉降和对桩基的影响，通过3组离心试验对不同的隧道-桩基间距情况进行分析。结果表明：隧道在近接侧穿越桩基时桩身最大轴力和弯矩都发生在隧道起拱线附近，而且桩基反应都是随着隧道-桩基间距的增加而减小。隧道-桩基间距Xpile较小时桩基沉降较为明显，但当Xpile>2.5R时桩基沉降可忽略不计。

Franza等[17]采用离心模型试验模拟了在高桩结构下的隧道开挖问题，隧道模型建立采用刚性的内芯，隧道端部使用一个柔性橡胶膜密封，控制隧道外边的液体体积模拟隧道地层损失，模拟隧道开挖对桩基和上部结构的影响。结果表明：隧道开挖产生的土体沉降应当使用修正高斯曲线进行拟合；桩基在工作状态下，上部荷载相同，桩基沉降随着隧道-桩基间距增大而减小。这与文献[4]，[14]，[15]试验结果相一致。

离心机能够将桩基、隧道和原位土体尺寸通过相似比进行缩减，同时可以克服由于模型尺寸缩小造成的自重应力损失，所以较之现场测量具有更高的可操作性。相似模拟试验的尺寸缩减也会带来尺寸边界效应的影响，使得结果在定量分析中会有一定的误差。

2 小孔扩张-收缩理论及应用

小孔扩张-收缩理论提供了解决复杂岩土工程问题的实用方法，因此在解决隧道-桩基相互作用问题时也可以作为解决方法之一。目前小孔扩张-收缩理论的研究主要体现在2个方面：①小孔扩张-收缩理论解析解的理论求解；②小孔扩张-收缩理论在工程问题中的应用。

2.1 岩土介质小孔扩张-收缩理论

岩土介质小孔扩张-收缩理论是研究岩土体在小孔扩张和收缩过程中所引起的应力、应变、孔隙水压力的变化。在理论推导过程中，需要将土体假设成均匀连续介质，借助连续介质原理和相应的本构模型求解，求解的难易程度取决于小孔扩张-收缩理论的边界假设(边界为位移不变或应力不变或有限边界或无限边界等)、土体假设的变形状态(大应变或小应变)及使用的本构模型(弹性模型、弹塑性模型、塑性模型、黏弹性模型、黏弹塑性模型、弹-脆性模型等)。自1945年Bishop等[18]最早提出，经过多年发展已求解出大量的解析解。Vesic[19]采用Mohr-Coulomb屈服准则和非关联流动法则，引入剪胀角来描述土体的剪胀特性，同时采用对数应变来考虑塑性区的大变形，提出了理想弹塑性土体中柱形和球形孔扩张的统一解，并采用Hill增量法严格推导了的原位状态小孔扩张解，建立了土体塑性半径随时间的变化关系。Collins[20]采用剑桥模型，考虑了土体体积应变速率和剪切应变速率，对正常固结和超固结黏土的小孔扩张过程进行分析，得到了超孔隙水压力和有效应力分布的解析解。Mo等[21]根据统一砂黏土理论模型(CASM)分别推导了排水条件下柱形和球形小孔扩张统一解。俞茂宏根据双剪统一强度理论求解了柱形和球形小孔扩张解析解。随着小孔扩张理论解的发展，不少学者对小孔收缩问题也进行了大量的研究，给出了在排水和不排水条件下基于Mohr-Coulomb屈服准则和临界土力学状态理论的应力、应变理论解[22]。Mo等[23]基于CASM模型，考虑土体开挖的大应变假设，推导了不排水条件下小孔收缩的统一理论解。

2.2 小孔扩张-收缩理论在桩基工程和隧道工程的应用

大量小孔扩张-收缩理论解析解为解决实际工程问题打下了良好的基础。Bishop等[18]在发现岩土介质开挖深孔所需压力与孔扩张所需压力之间存在一定的比例关系后，首次提出小孔扩张与静力触探试验之间具有相似性。目前小孔扩张-收缩理论已经成功解释了原位静力触探试验(Cone Penetration Test，CPT)中锥尖贯入阻力的大小，如图4所示，其中d为桩直径，qc为锥尖贯入阻力，α为锥尖角度。

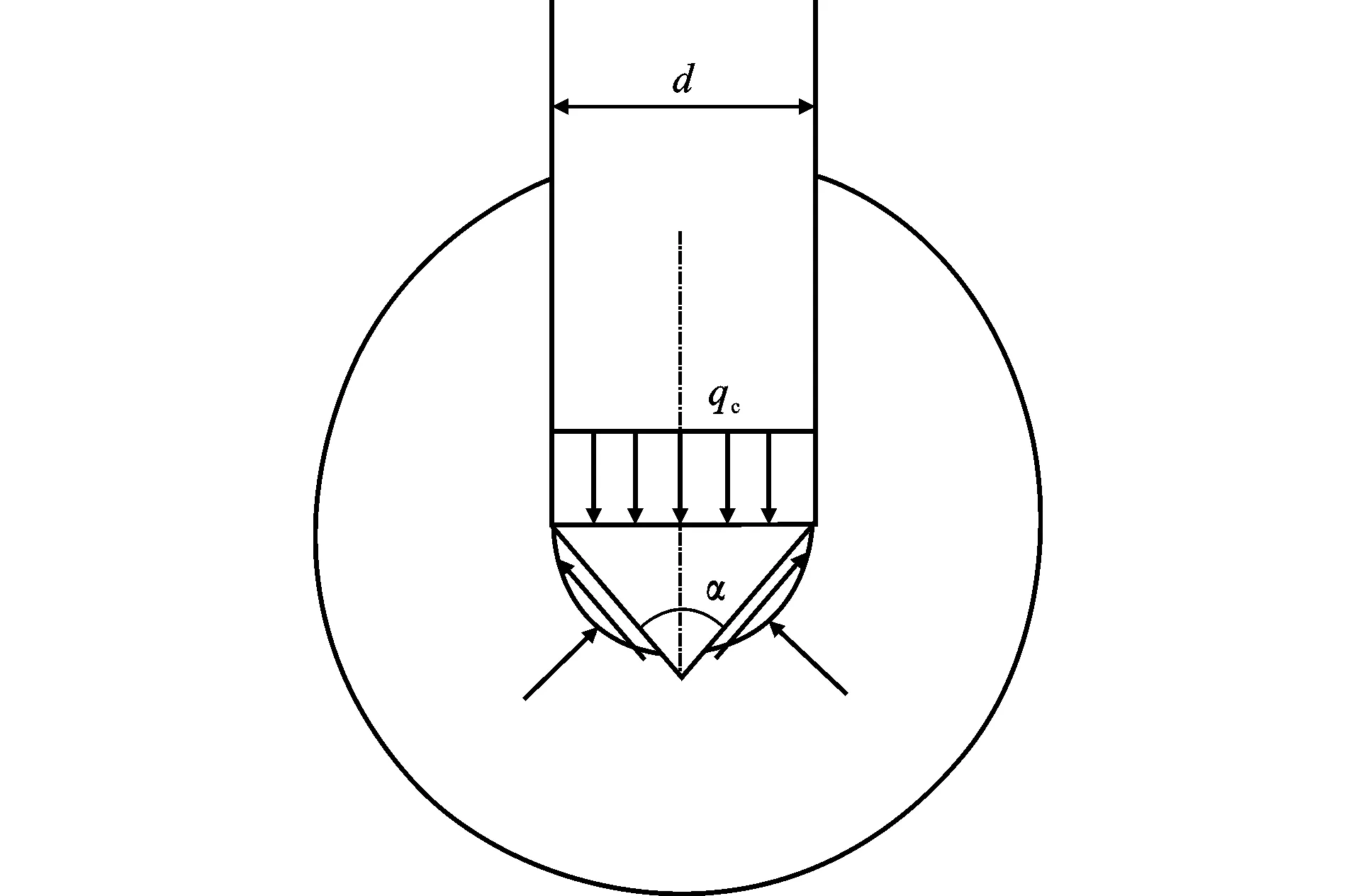
图4 锥尖贯入阻力和小孔扩张孔压关系Fig.4 Relationship Between Cone Tip Resistance and Cavity Expansion Pressure

Suzuki等[24]采用二维有限元软件在饱和砂土模拟静力触探试验(CPT)过程，考虑圆锥锥面的法向应力的角度与圆锥顶点角度的几何关系，得到了球孔扩张孔压与贯入阻力的关系，并与试验结果进行验证。桩基在打桩过程中会将周围的土体挤向四周，形成挤土效应。由于挤土桩和静力触探试验的几何相似和力学相似，桩端承载力看作球形小孔扩张，桩侧阻力可看作柱形小孔扩张进行计算。Yasufuku等[25]建立桩端承载力、小孔扩张压力和土体摩擦角的关系。

隧道开挖过程可以看作是土体从原位状态卸载的工程问题，小孔扩张-收缩理论模型可以很好地分析这一问题。将隧道开挖假设为理想轴对称图形，对于隧道掘进段的求解分为2个部分：①土体掘进方向的端部采用球形小孔收缩；②隧道轴线部分假设为柱形小孔收缩，如图5所示，其中D为隧道外径，衬砌安装在工作面后方距离P处，δ，δ1，δ2分别代表拱背处、未衬砌处和衬砌处径向土体变形。

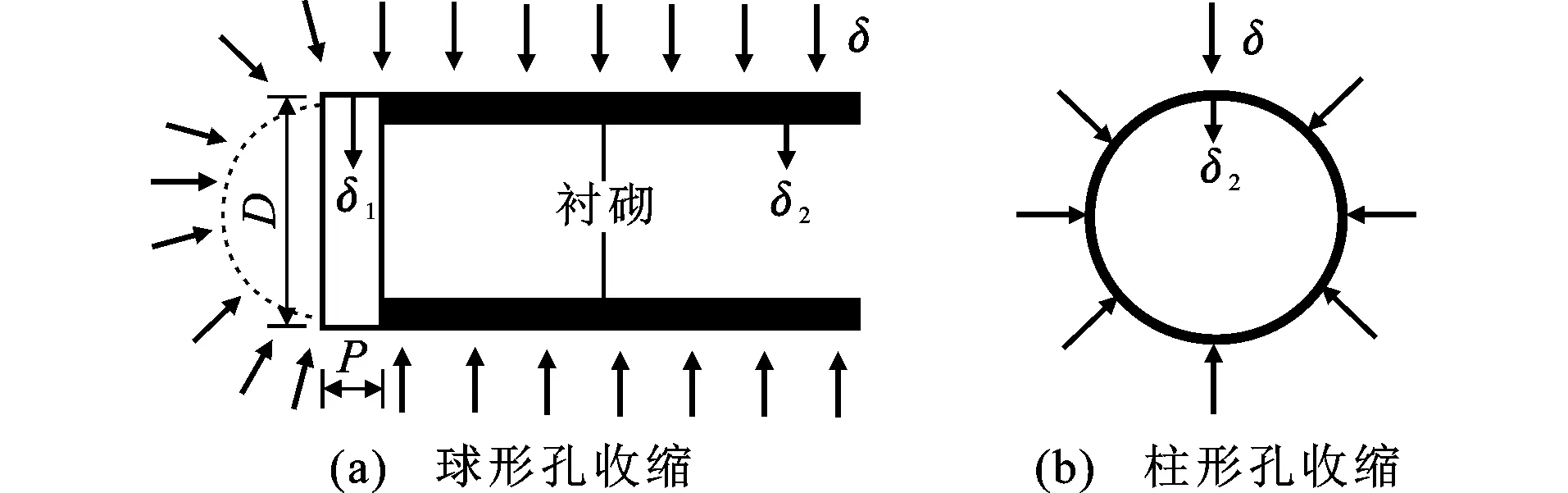
图5 小孔收缩在隧道工程的应用Fig.5 Application of Cavity Contraction Method in Tunnel Engineering

Mair等[26]假设土体为理性线弹性材料的Treasca材料，预测黏土中隧道开挖引起的地面变形和孔隙压力变化。Yu等[27]分别采用原始剑桥模型、修正剑桥模型和CASM模型对伦敦不饱和黏土预测了隧道开挖对土体的超孔隙水压力、土体应力的影响。Mo等[23]预测了不排水条件下隧道开挖引起的土体应力和超孔隙水压力的影响，并分析了土体的状态参数对土体应力变化的影响。结果表明：土体的状态参数对径向有效应力和切向有效应力的影响较小；土体有效应力随着间距比的增加明显变大；负超孔隙水压力随着间距比的增大而减小，当间距比较大时，正孔隙水压力出现。

3 浅埋隧道开挖对邻近桩基影响

小孔扩张-收缩理论能够为隧道-桩基相互作用问题提供新的分析方法。Marshall[28]基于Mohr-Coulomb准则，采用柱形小孔扩张理论模拟开挖过程，计算隧道开挖对周围土体的影响，球形小孔扩张理论计算桩端阻力，运用修正β法计算桩周摩阻力。通过控制隧道地层损失比计算土体的应力场和刚度衰减，并提出桩基承载力衰减因子，研究不同隧道-桩基间距下桩基承载力衰减因子的大小。结果表明：当隧道衰减因子为0.85时，桩基发生破坏。在此基础上，张治国等[9]采用两阶段分析法，在阶段一采用基于Mohr-Coulomb准则下的柱形孔收缩理论计算隧道开挖引起的土体位移场，在阶段二采用Pasternak计算桩基弹塑性水平位移，并与离心试验结果进行对比，分析了不同土体参数和隧道-桩基间距与地层损失的关系。莫品强等[29]考虑了土体的应变硬化/软化特性，基于CASM模型分析了隧道开挖对邻近挤土桩的沉降影响，采用球形小孔扩张理论计算桩端阻力，UWA-05法计算桩侧阻力，柱形小孔收缩模拟隧道开挖过程，得到了开挖后桩基承载力理论值，并提出了隧道的安全系数，根据桩基承载力、桩基安全系数及桩基沉降依次提出桩基承载力控制、稳定控制准则和变形控制准则，并以桩基变形控制准则为核心进行桩基承载力的验算。当前学者所采用的小孔扩张收缩模型是假设土体为无限远场，针对深埋隧道开挖，该假设是合理的。针对浅埋隧道开挖，由于地表的存在，土体的边界条件产生变化，应该采用有限介质小孔扩张-收缩理论进行求解，边界条件为

σr|r=a=-p

(1)

σr|r=b=-p0

(2)

式中：σr为土体的径向应力；r为极坐标下半径，表示土体内任意点到土体中心的距离；a，b分别为土体扩张后小孔的内径和外径；p为扩张后土体内壁孔压；p0为土体外壁孔压。

对于浅埋隧道开挖对桩基影响的求解，可假设为小孔在有限介质土体内进行收缩，小孔外壁半径可取隧道中心至地表的距离，同时由于土体地表的存在，地表应力为0，故需基于土体原位应力场的分布，对有限小孔收缩求得的土体应力场进行修正。隧道与邻近桩基的相互作用可按照Marshall等[30]的方法简化为二维模型进行分析，模型图如图6所示，其中zt为埋深，zp，bp，rp分别为桩深、桩直径和桩半径，dtp，ztp，xtp分别为A，B两点间直线距离、竖直距离和水平距离。

图6 隧道-桩基几何模型Fig.6 Geometric Model of Tunnel-pile Foundation

计算模型可分为3个部分：

(1)桩基承载力。桩基在打桩过程时，桩端部分可看作球形小孔扩张过程计算桩端阻力。由于考虑地表效应的影响，采用有限介质小孔扩张理论时球形孔扩张外边界可取为桩长，小孔的初始半径相当于土颗粒半径。桩侧摩阻力可按照Randolph进行计算，但由于桩基在打桩过程中会对周围土体有挤密剪胀作用，土体周围有一个柱形弹性小孔剪胀带，计算时应加以考虑，同时土体的应力场在打桩过程中发生改变。在桩基打桩完成后，基于桩基施工后的土体应力场，桩基承载力的计算依据10%沉降原则，小孔初始半径从桩径扩张至1.1倍桩径，初始应力水平应取土体塑性区的平均应力计算。

(2)隧道开挖。基于打桩后的土体应力场，考虑土体的地表效应，将有限介质小孔外边界取为隧道中心至地表的距离，土体采用有限介质柱形小孔收缩模拟隧道开挖的应力-位移曲线。根据Verruijt等[6]的方法，考虑隧道的地层损失和椭圆度的影响计算土体的位移值，然后根据开挖的应力-位移曲线得到隧道开挖后土体的应力变化量，由于地表的应力值为0，将得到的土体应力改变量按照土体的地应力分布进行修正，然后与打桩后的土体应力场相加得到隧道开挖后的土体应力场。

(3)根据改变后的土体应力场，计算桩端阻力和桩侧承载力，得到衰减后的桩基承载力。将桩基承载力衰减因子定义为衰减后的承载力与原有承载力的比值。由于隧道开挖造成土体的应力场改变，土体的刚度和强度降低，使得桩基在原有荷载的情况下发生沉降，因此可将桩基沉降分为2个部分：①隧道开挖引起的桩基位置的土体沉降，可通过在第(2)部分中得到的土体位移场的数值分量得到；②根据桩基承载力衰减后引起的桩基沉降和得到的桩基承载力和土体的刚度，采用双曲渐近模型对桩基沉降进行预测。浅埋隧道-桩基力学模型计算流程如图7所示，其中Vl,t为地层损失量，a0为孔隙初始半径，取平均粒径的一半，即d50/2。

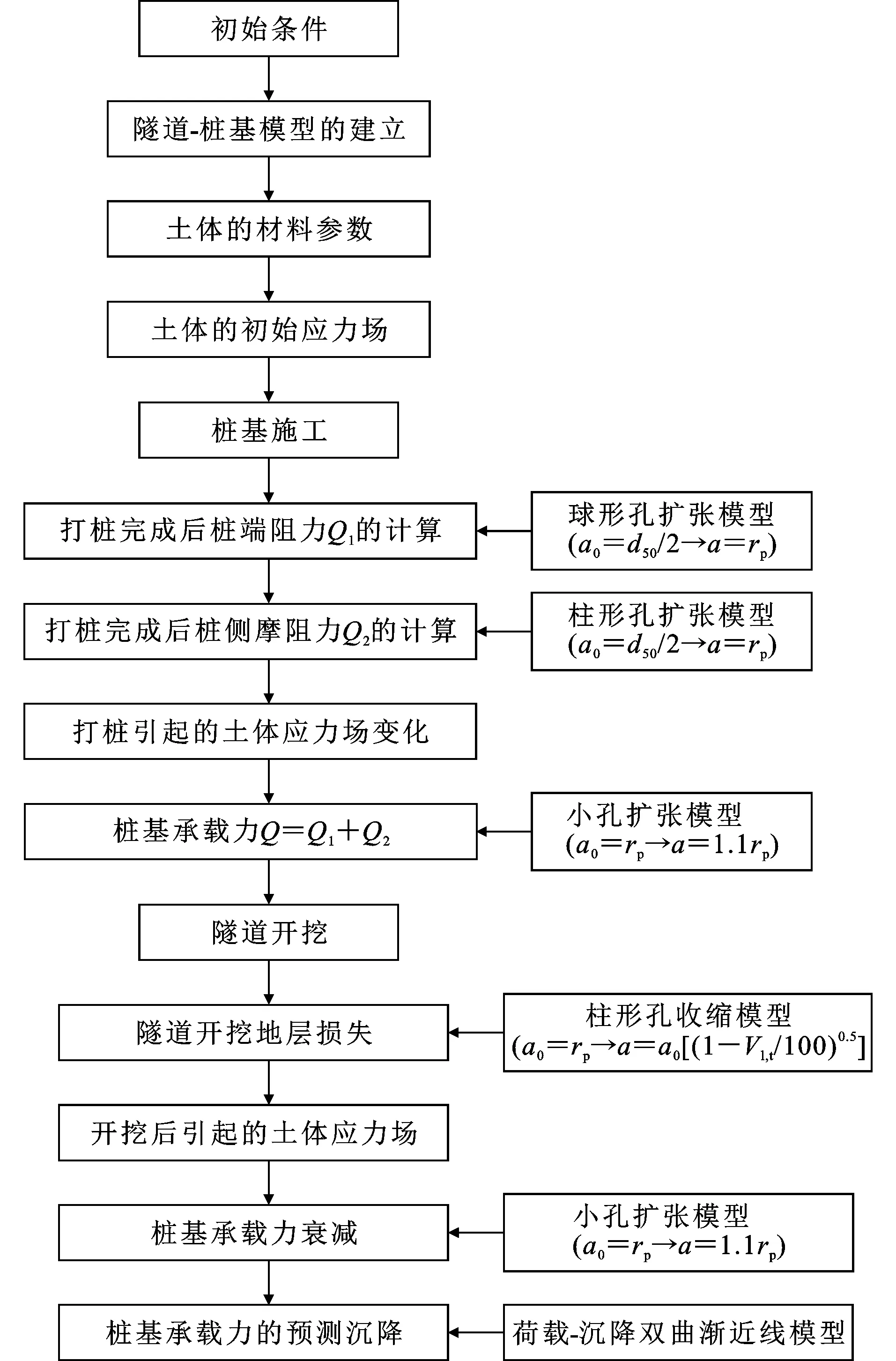
图7 隧道-桩基模型的计算流程图Fig.7 Calculation Flowchart for Tunnel-pile Foundation Model

Marshall[15]针对隧道开挖对桩基影响进行了在砂土中的离心模型试验。试验砂土采用Leighton Buzzard砂土，土体的相对密度Gs=2.67，平均粒径d50=0.122 mm，最小孔隙比emin=0.64，最大孔隙比emax=0.97，泊松比ν=0.2，离心加速度N=75g(g为重力加速度)。隧道半径R=6 mm，埋深zt=20 mm，桩半径rp=62 mm，桩深zp=10 mm，隧道处于桩基正下方。

图8为相同地层损失隧道开挖产生的土体竖向位移场Sv。由图8可以看出，隧道开挖后土体的最大沉降发生在隧道顶部正上方。地层损失比为1%时，土体最大位移大致为0.2 mm，理论计算土体竖向位移值为0.2 mm，土体地表的最大沉降值为0.15 mm，理论计算土体竖向位移值为0.13 mm；当地层损失比为5%时，土体最大位移大致为1 mm，理论计算土体竖向位移值为0.95 mm，土体地表的最大沉降值为0.4 mm，理论计算的土体竖向位移值为0.6 mm，这与试验结果相吻合，验证了计算方法的可靠性。

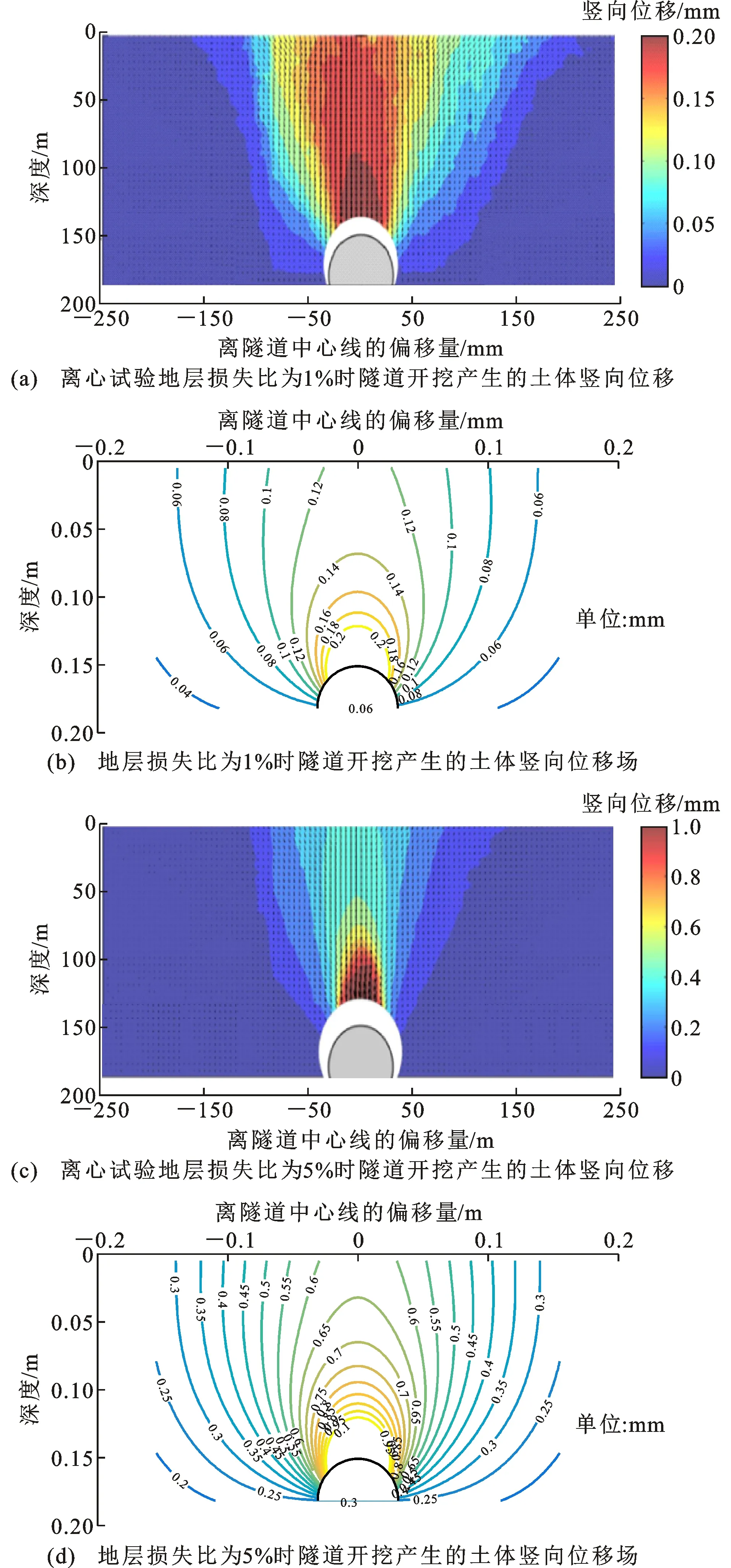
图8 相同地层损失隧道开挖产生的土体位移场对比Fig.8 Comparisons of Soil Displacement Fields Caused by Tunnel Excavation at the Same Volume Loss

图9给出了地层损失比为5%时隧道-桩基相互作用各阶段应力场及应力场改变量。图9(a)为初始地应力场，土体的应力随着深度增加呈线性增长。图9(b)为桩基打桩后土体应力场，由于桩基的挤入过程，桩周土体应力增大。桩端部分的土体应力增长较为明显，土体塑性区范围大约为桩侧土体的5倍。图9(c)为隧道开挖引起的土体应力场改变量。可以看出土体的应力场改变在隧道顶部改变量最大，土体应力场改变范围与Jacobsz等[4]提出的隧道开挖对桩基的整体影响区域大致相同。图9(d)为打桩和隧道开挖后土体的应力场。可以看出桩基周围的土体应力场明显减小，这将会导致桩基的沉降和承载力衰减，严重时桩基将会发生失稳破坏。

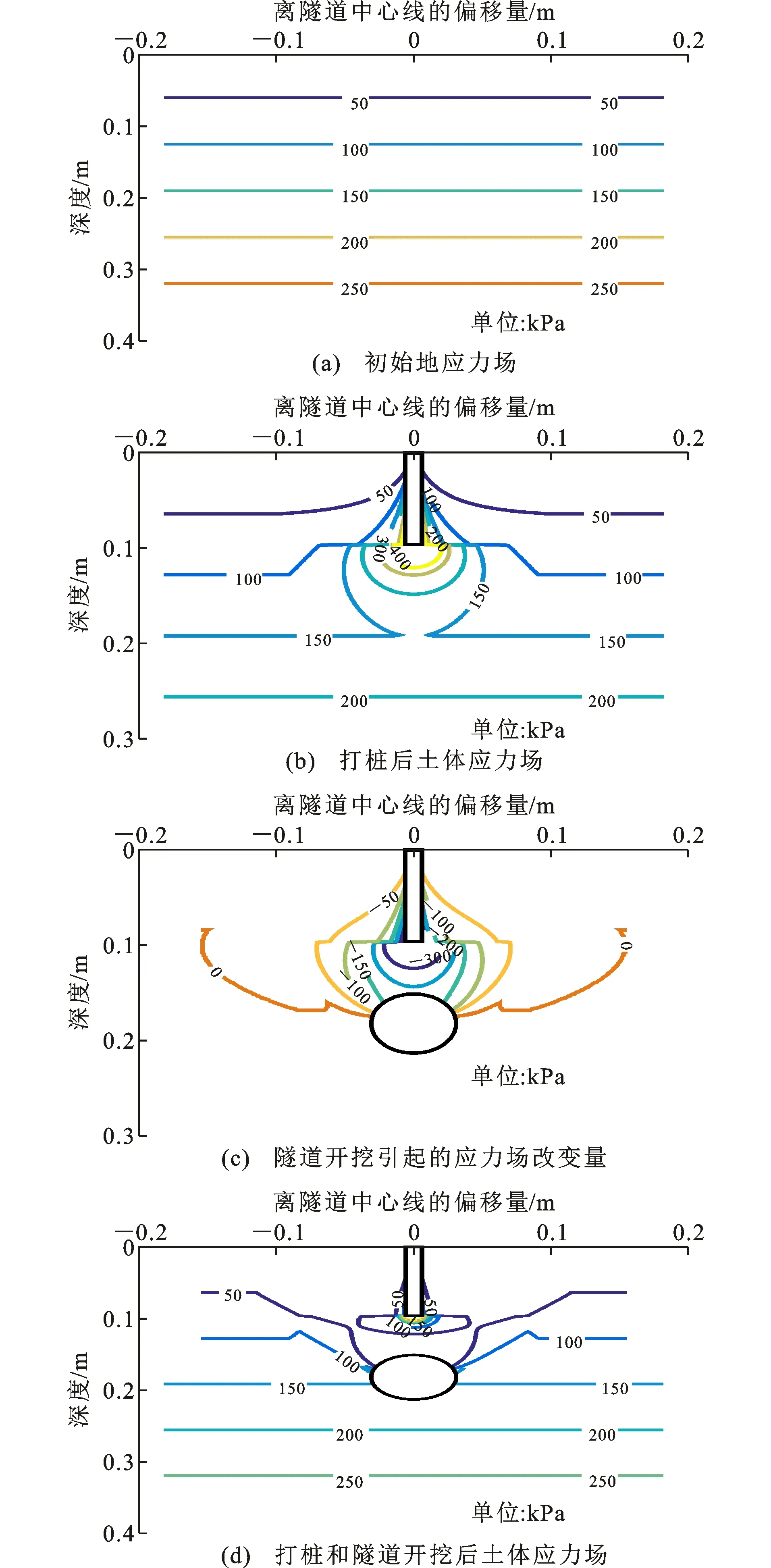
图9 地层损失比为5%时隧道-桩基相互作用各阶段土体应力场Fig.9 Stress Fields at Each Stage of Tunnel-pile Foundation Interaction when Volume Loss Is 5%

图10为不同地层损失下隧道开挖对桩基刚度ki、承载力衰减系数RQ、桩端承载力Qtip和桩侧承载力Qshaft的影响。图11为不同地层损失下桩基的承载力特征曲线。可以看出，随着地层损失不断增大，隧道开挖后桩基的刚度不断减小，这是由于隧道开挖后，桩基周围的土体应力水平下降导致土体剪切模量下降。桩基承载力衰减因子不断减小，说明隧道开挖后桩基承载力不断减小。图10(c)，(d)说明了桩端承载力和桩侧阻力随着地层损失的变化。可以看出桩端阻力和桩侧承载力分别从1 800 N和2 050 N迅速衰减至700 N，说明桩基在隧道开挖时受到影响，承载力衰减迅速，这也解释了图9中桩基沉降的变化趋势，当桩基沉降超过某一限值时，桩基将产生失稳现象。

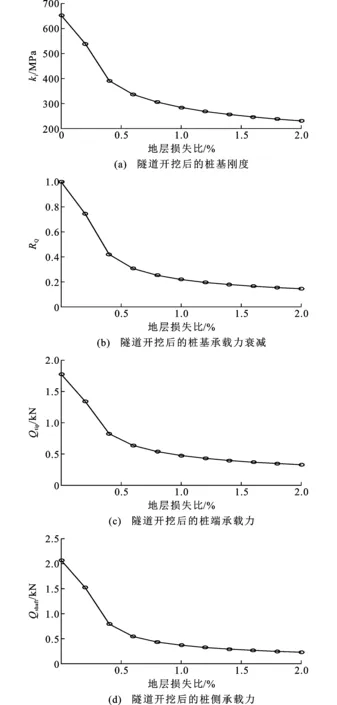
图10 不同地层损失下隧道开挖对桩基刚度、承载力衰减系数、桩端承载力和桩侧承载力的影响Fig.10 Effects of Tunnel Volume Loss on Pile Stiffness, Bearing Capacity Degradation and Pile Bearing Capacity

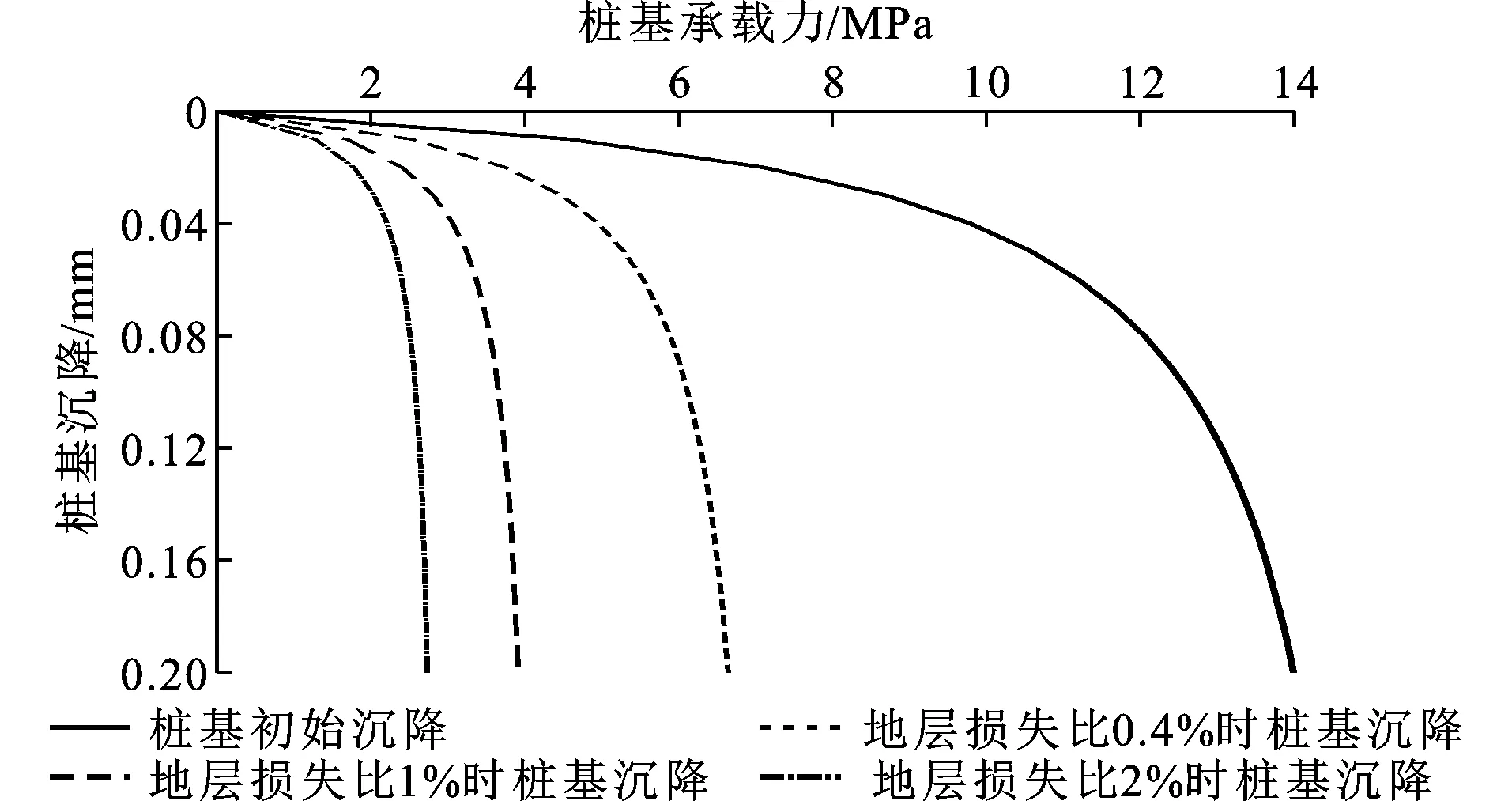
图11 不同地层损失下桩基承载力特征曲线Fig.11 Bearing Capacity Characteristic Curves of Pile Foundation Under Various Tunnel Volume Loss

4 结 语

(1)数值模拟方法是目前在岩土工程中广泛采用的方法，这是由于隧道开挖与邻近桩基的相互作用是一个复杂的工程问题，实际工程中也很难对隧道-桩基进行监测。现有的经验公式由于没有经过严格的理论推导，在实际工程中会出现一些局限性。理论计算方法得出的解析解对于土体的假设较多，无法反映岩土介质的综合影响，同时现有理论中大多数考虑桩基的水平位移，对于隧道开挖引起的桩基沉降研究较少。

(2)本文总结了小孔扩张-收缩理论在隧道-桩基相互作用分析中的应用，指出现有小孔扩张-收缩理论在研究浅埋隧道开挖的不足，提出了采用有限介质小孔扩张-收缩理论对浅埋隧道开挖与邻近桩基的影响进行分析研究，并给出了初始的计算模型和计算流程图，通过与离心试验结果进行对比验证了此方法的可行性，同时指出小孔扩张-收缩理论可以考虑三维隧道开挖对邻近桩基的影响，为解决隧道-桩基相互作用提供新的解决思路。