基于覆盖粗糙Vague软专家集的动物疾病诊断算法

陈鹏岗,冯晓毅

(1.西安交通大学第二附属医院 信息网络部,陕西 西安 710004;2.西北工业大学 电子信息学院,陕西 西安 710072)

Vague集[1]和软集[2]都是处理不确定性理论的基本数学模型。Vague软集是[3]将Vague集和软集相融合，基于各自数学特征提出的一种新的扩展理论模型。Vague软集是数据挖掘领域中一种处理不确定性问题的新型数学工具，已被成功应用于模式识别、模糊决策、评估评价、舆情分析等诸多研究领域[4-11]。实践证明，任何单一的理论模型都很难单独完整描述并解决现实问题，因此探讨各类Vague软集的扩展模型及其应用问题，有着较强的现实意义和研究价值。近年来，学者研究了Vague软集与软专家集[12]融合以及与覆盖粗糙Vague集[13]融合的问题，并提出了一系列扩展模型。文献[14]将Vague软集和软专家集两种理论融合扩展，首次提出了Vague软专家集的概念，为研究不确定性问题奠定了新的理论基础。文献[15]进一步拓展了Vague软专家集的定义，提出了广义Vague软专家集的概念，并讨论了相关性质和基本关系问题。文献[16]介绍了广义Vague软专家集的映射并对其运算进行了研究。文献[17]将中性软专家集与中性Vague集理论相融合，提出了新的中性Vague软专家集数学模型，研究了基本操作和一些相关性质，并将此模型应用到一个决策问题中来说明其有效性。文献[18]将区间值Vague软集的概念进行推广，提出了可能性区间值Vague软专家集的概念，并研究了该模型的相关代数性质和相似性度量以及实例。文献[19]基于复杂Vague软专家集方法研究了工程质量可靠性评价问题，为Vague软专家集模型的应用问题提供了思路。文献[20]将覆盖粗糙Vague集和Vague 软集进行融合，提出了一种新的处理不确定性问题的数学模型，即覆盖粗糙Vague 软集，并研究了相关性质及在疾病诊断问题中的应用。本文在上述研究成果的基础上，分析了现有模型在疾病诊断等决策问题中的局限性，进一步将覆盖粗糙Vague集与Vague软专家集理论进行融合，提出了新的覆盖粗糙Vague 软专家集数学模型，并研究了该模型的相关性质和关系运算问题。最后，本文提出了一种基于覆盖粗糙Vague 软专家集的动物疾病诊断算法。

1 现有模型的不足

Vague集[1]理论如下：

定义1设U是一个论域，对于U的任意一个元素x，U中的一个Vague集A由真隶属度函数tA和假隶属度函数fA所描述，如下所示。

(1)

满足0≤tA+fA≤1，其中tA(xi)是支持x∈A的证据的隶属度下界，fA(xi)是反对x∈A的证据的隶属度下界。称πA(xi)=1-tA(xi)-fA(xi)为x对于Vague集A的不确定度(未知度)，是x相对于A的未知信息的一种度量。显然0≤πA(xi)≤1，πA(xi)值越大，说明x对于Vague集A的未知信息越多。

文献[2]通过引入参数化思想提出了软集理论：

定义2设U是一个论域，P(U)是U的幂集，E是一个参数集，A⊆E，且F:A→P(U)是一个映射，称(F,A)为U上的一个软集。

文献[3]首次将Vague集与软集理论进行融合，提出了Vague软集理论：

定义3设E是一个参数集，A⊆E，且F:A→P(U)是一个映射，即∀e∈A，F(e)为U上的一个Vague集，称(F,A)为U上的一个Vague软集。

文献[12]提出了软专家集的定义：

定义4设U是一个论域，E是一个参数集，X是一个专家集，O是一个意见集，设Z=E×X×O，A⊆Z，且F:A→P(U)是一个映射，P(U)表示U上所有子集的集合(幂集)，则称(F,A)为U上的一个软专家集。

文献[13]将覆盖粗糙集与Vague集模型进行融合，提出了覆盖粗糙Vague集模型：

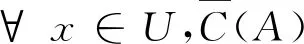
(2)

(3)

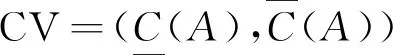
其中，Md(x)为x的最小描述。有

Md(x)=

{K∈C|x∈K∧(∀S∈C∧x∈S∧S⊆K⟹K=S)}

(4)

∩{K|K∈Md(x)}称为x的近邻域，记为CN(x)。

文献[14]提出了Vague软专家集模型：

定义6设U是一个论域，E是一个参数集，X是一个专家集，O={1=同意,0=不同意}是一个意见集，设Z=E×X×O，A⊆Z，且F:A→VU是一个映射，即VU表示U上所有Vague子集的集合，称(F,A)为U上的一个Vague软专家集。

文献[20]进一步将覆盖粗糙Vague集与Vague软集模型进行融合，提出了覆盖粗糙Vague软集模型：

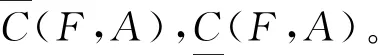
(5)

(6)

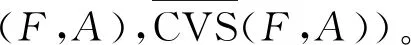
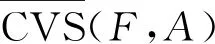
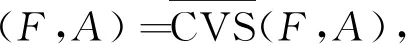
研究发现，动物疾病的诊断过程是一个将各种动物疾病数据资料经过分析评价后，对所患疾病提出一种诊断结果符合逻辑思维的复杂过程。如果这种逻辑决策过程符合动物疾病诊断的客观实际，则这种诊断就是正确的；若不符合，则诊断结果就会出现误差。在研究基于数据挖掘技术的动物疾病诊断算法时，由于动物病情变化具有复杂性且兽医专家认识水平有局限性，故诊断数据模型的选择至关重要。诊断模型的选择越符合客观实际的诊断过程，则诊断的准确率也更高。

但是，在将上述几种模型应用于动物疾病实际诊断问题时，文献[13]提出的覆盖粗糙Vague集模型仅部分考虑了覆盖粗糙集的一般性和Vague集的“支持”、“反对”、“弃权”3个方面的决策因素，没有考虑疾病诊断对象本身的参数特征，因此有一定的局限性。文献[14]提出的Vague软专家集模型没有考虑基于覆盖粗糙集对病例数据进行随机划分时的一般性。文献[20]提出的覆盖粗糙Vague软集模型虽然考虑了覆盖粗糙集的一般性和Vague集的“支持”、“反对”、“弃权”3个方面的决策因素，也兼顾了诊断对象本身的参数特征，但是该模型没有充分考虑专家意见集，故不符合动物疾病诊断的客观实际需求。在实际诊断时，经常需要不同兽医专家的会诊，因此专家意见集的影响因素也同样重要。

本文针对基于Vague软集扩展模型的动物疾病辅助诊断过程需要考虑的决策因素进行了详细说明，如表1所示。

表1 动物疾病诊断决策因素分析

由表1可以看出，将不同数学模型应用于疾病诊断过程时，不同的诊断步骤涉及到的决策影响因素是不一样的。覆盖粗糙集、Vague集、软集和软专家集在表征疾病诊断对象和诊断过程中发挥的影响因素缺一不可，必须全面综合考虑各自的数学特征。因此，有必要进一步将覆盖粗糙集、Vague集、软专家集3种理论模型进行融合，提出新的更符合客观实际的Vague软集融合理论模型，以提高疾病诊断的准确率。

2 新的覆盖粗糙Vague软专家集

进一步将覆盖粗糙Vague集和Vague软集、软专家集3种模型进行融合，定义一种新的覆盖粗糙Vague软专家集理论模型。

2.1 新的覆盖粗糙Vague软专家集的定义

(7)

(8)

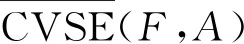
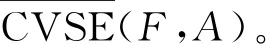
2.2 几种数学模型的逻辑关系

总结Vague软集、软专家集、Vague软专家集、覆盖粗糙集、覆盖粗糙Vague集、覆盖粗糙Vague软集和本文提出的覆盖粗糙Vague软专家集的逻辑关系，如图1所示。

图1 几种数学模型的逻辑关系图Figure 1. Logical relation diagram of several mathematical models

从图1可以看出，Vague软集的数学本质是具有Vague集区间特征的软集。Vague软专家集的数学本质是具有Vague集区间特征的软专家集。覆盖粗糙Vague集的数学本质是上下近似算子均为Vague集的覆盖粗糙集。覆盖粗糙Vague软集的数学本质是上下近似算子均为Vague软集的覆盖粗糙集。覆盖粗糙Vague软专家集的数学本质是上下近似算子均为Vague软专家集的覆盖粗糙集。

2.3 覆盖粗糙Vague软专家集的性质

覆盖粗糙Vague软专家集具有以下重要性质。

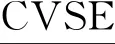
(1)

(9)

(2)

(10)

(3)可加性1为

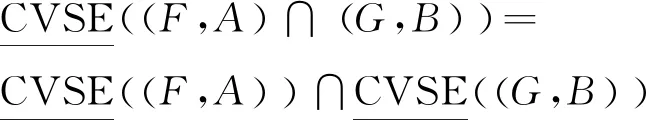
(11)

(4)可加性2为

(12)

(5)单调性

(13)

(6)

(14)

(7)幂等律

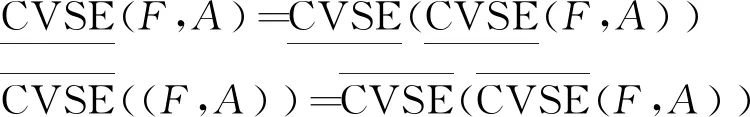
(15)

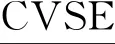
3 基于覆盖粗糙Vague软专家集的动物疾病诊断算法

在动物疾病的诊断过程中，诊断专家需要根据待诊断的动物病例信息进行判断，从中选出最符合疾病特征的病例做出决策。上述问题的决策过程如果完全凭借诊断专家的经验显然是不现实的，应基于新的覆盖粗糙Vague软专家集数学模型对该问题进行讨论。

分析发现，养殖场送检的动物病例的患病水平对于诊断专家进行决策十分重要，但是送检者一般都不愿意公开所养殖动物的真实患病水平，以免影响养殖场的经济效益和社会效益。为解决上述问题，需要根据送检者送来的其他病例信息来预测送检病例的患病水平，以供诊断专家进行诊断决策，并以发病程度作为决策因素进行预估。

算法过程描述如下：

输入：专家给出的待诊断对象病例x的发病程度评价集，待诊断对象发病程度数据集(以3个Vague软专家集high、middle、low表示)。

输出：待诊断对象病例x的患病水平隶属度函数值。

步骤1生成覆盖近似空间C。根据待检测的疾病发病程度生成论域U上的一个覆盖，C={重,一般,轻}；

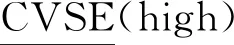
SF(ei)(xj)=|tF(ei)(xj)-fF(ei)(xj)|

(16)

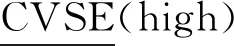
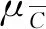
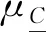
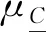
步骤6 建立患病水平隶属度函数值和发病程度之间的关系表格；

步骤7 建立患病水平隶属度函数值和病例之间的决策表格。

以非洲猪瘟的疾病诊断为例，对算法过程进行详细描述。

设某兽医站要对猪场提供的一组病猪病例进行非洲猪瘟疾病的诊断，论域(U,C)为猪场提供的5组猪病例xi(i=1,…,5)，3个专家p、q、r分别对5组病猪的发病程度评价如下：

专家p

(17)

专家q

(18)

专家r

(19)

根据待检测的病猪发病程度，能够得到论域U上的一个覆盖，C={重,一般,轻}。

其中

(20)

即

C={{x1,x2,x3},{x2,x3,x4,x5}，{x3,x4,x5}}

(21)

由于非洲猪瘟疾病病例数据主要包括发热、呼吸困难、脏器出血等3个病理特征，用一个参数集E={e1,e2,e3}来表征，则可以用论域U上的3个Vague软专家集high、middle、low表征待检测的病猪发病程度

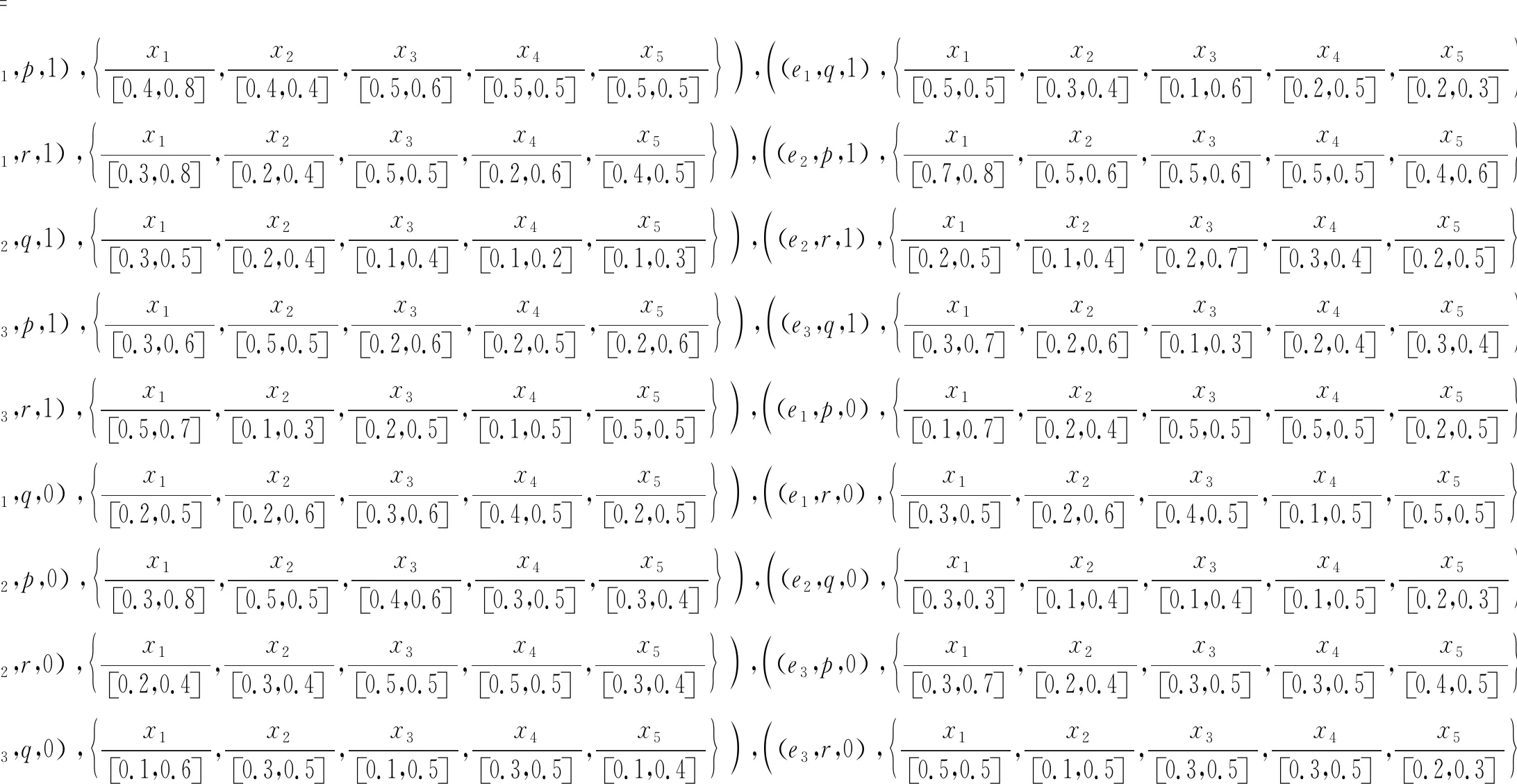
(22)

(23)

(24)

计算上下近似为

(25)

(26)

同理可以计算Vague软专家集middle、low在覆盖空间C上的上下近似，并基于隶属度函数建立患病水平和发病程度之间的关系。

为决策方便，基于Vague软集的核函数作为记分函数，即式(16)，将3个Vague软专家集high、middle、low在覆盖空间C上的上下近似转化为模糊软专家集。

分别计算发病程度{重}隶属于high、middle和low的隶属度函数值，步骤如下：

步骤1计算发病程度{重}隶属于high的最小、最大隶属度分别为

(27)

当送检病猪的发病程度为重时，则可推测病猪患病水平为high的程度为[0.07,0.11]之间；

步骤2计算发病程度{重}隶属于middle的最小、最大隶属度分别为

(28)

当送检病猪的发病程度为重时，则可推测病猪患病水平为middle的程度为[0.03,0.14]之间；

步骤3计算发病程度{重}隶属于low的最小、最大隶属度分别为

(29)

当送检病猪的发病程度为重时，则可推测病猪患病水平为low的程度为[0.08,0.1]之间。同理，可以计算出发病程度{一般}隶属于high、middle和low的隶属度和发病程度{轻}隶属于high、middle和low的隶属度。

在此基础上，建立患病水平和发病程度之间的关系表格，如表2所示。

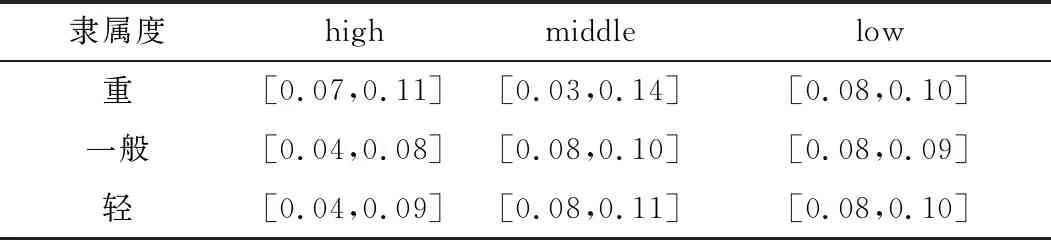
表2 关系表格

由表2可以预测出5组病例xi(i=1,…,5)的患病水平隶属度值，建立决策表格，如表3所示。

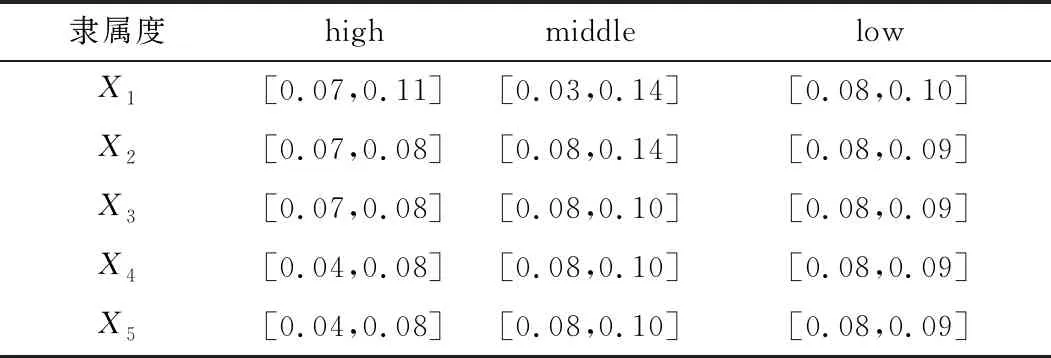
表3 决策表格

由表3可以看出，若已知专家对发病程度的评价，则可以依据上述决策算法预测出该病例的发病水平，对非洲猪瘟疾病的诊断提供一定的辅助决策支持。

4 实验结果及分析

4.1 实验环境

本文中，CPU型号为Intel Xeon7420四核64位处理器，频率为2.13 GHz，内存大小为64 GB，硬盘大小为6 TB，操作系统为Windows7。编程语言选择Visual Basic，数据库软件选择Microsoft Office Access。

4.2 实验数据及评价标准

数据集选取某兽医站动物疾病病例数据库，以疾病的诊断准确率作为算法的评价标准。

4.3 实验结果

在上述数据集上进行有效性验证。结果表明，本文提出的基于覆盖粗糙Vague软专家集的动物疾病诊断算法对疾病诊断的准确率达90%以上。算法测试结果如表4和图2所示。

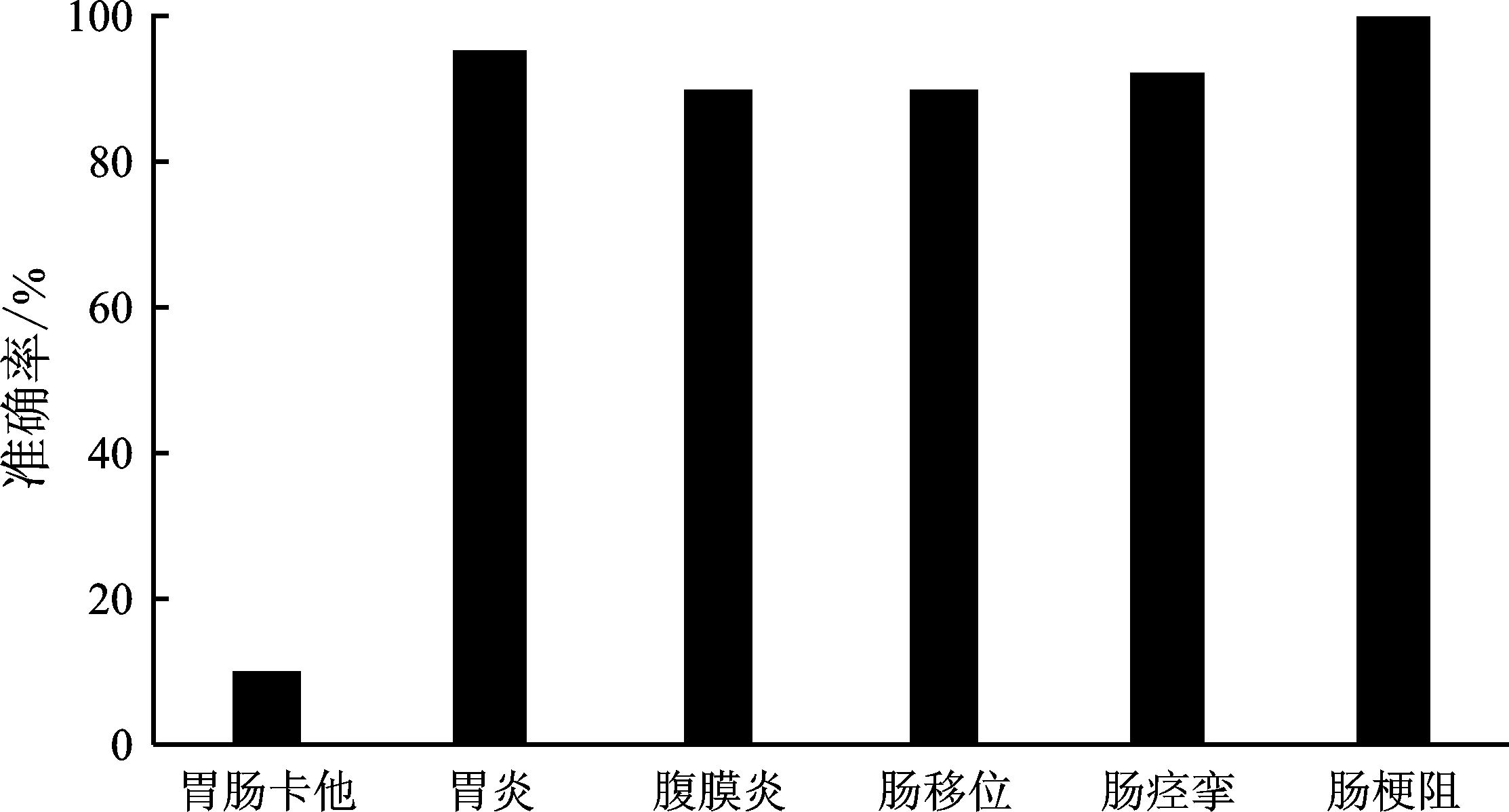
图2 测试结果Figure 2. Test results

选取两种基于Vague软集扩展模型的动物疾病诊断算法，即ADADA_CRVS算法(基于覆盖粗糙Vague集的动物疾病诊断算法)和ADADA_CRVSS算法(基于覆盖粗糙Vague软集的动物疾病诊断算法)与本文提出的ADADA_CRVSES算法(基于覆盖粗糙Vague软专家集的动物疾病诊断算法)进行对比分析，实验结果如表5所示。

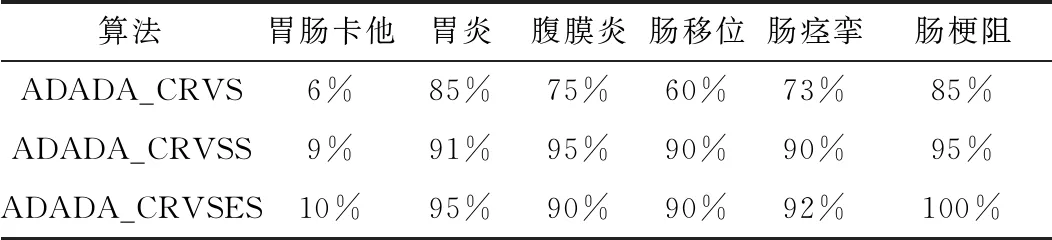
表5 测试结果对比

由表5可以看出，相较于ADADA_CRVS算法和ADADA_CRVSS算法，ADADA_CRVSES算法在疾病诊断的准确率上有了明显的提升。这是因为覆盖粗糙Vague软专家集作为模糊数学中一个新的理论模型，其相比覆盖粗糙Vague集和覆盖粗糙Vague软集而言考虑的决策因素更全面，既充分考虑了覆盖粗糙集的一般性，也考虑了Vague集“支持”、“反对”、“弃权”3个方面的属性因素和软集的参数特征，同时也兼顾了专家意见集的影响因素。其表达模糊性的能力更强更具体，更适合描述现实生活中的决策对象特征。

5 结束语

本文从Vague软集和软专家集的融合理论及应用问题出发，在分析已有Vague软集扩展模型的基础上，定义了一种全新的覆盖粗糙Vague软专家集数学模型，并探讨了该模型的数学性质和基本运算，同时给出了一种基于覆盖粗糙Vague软专家集的疾病诊断算法。动物疾病诊断中的应用实例表明，该算法是实用的和有效的。覆盖粗糙Vague软专家集数学模型在疾病诊断等模糊决策问题中具有较好的应用前景。