基于定向充电模型的最大化网络累计充电增益
2021-06-01章豪,王然
章 豪,王 然
(杭州电子科技大学 计算机学院,浙江 杭州 310018)
在无线传感器领域中,无线能量传输技术的出现与发展为解决传感器节点充能问题提供了新的思路,保证了网络的正常工作。无线能量传输技术与从所处环境中得到能量的技术不同[1-3]。无线能量传输技术通过在网络中部署调度移动充电小车对传感器进行无线充电,能够更加稳定地为网络充能,提高了充电效率[4-6]。
随着技术的进步,将能量传输形式抽象为单对单充电和单对多充电两种模型。单对单充电模型指充电器每次只对单个节点充电,该模型使用电感耦合技术[7-8],其有效充电距离一般在20 cm以内,需近距离进行能量传输。单对多充电模型指充电器同时为多个节点充能,可分为全向无线充电和定向无线充电。全向无线充电采用磁共振耦合技术,不受充电方向限制。文献[9]通过实验证明了能量可以在磁共振体之间进行传输,并且不需要任何媒介。例如,为2 m外的一盏60 W白炽灯供电的效率可以达到40%。定向无线充电要求节点在一定的距离与角度范围内,该模型采用电磁波辐射技术,在能量传输及接收设备中使用高增益定向天线,提高了能量传输效率,使其覆盖距离更远,例如毫米波蜂窝网络[10]。
研究人员对于定向无线充电模型进行了研究与应用。文献[10]研究了部署固定数量充电器的方式,最大化网络中节点能够接收到的充电效率。文献[11]假设网络所使用的节点接收能量也受方向限制,节点和充电器必须处于相对方向才能够进行能量传输。该研究解决的问题是不论节点朝着哪个方向都能够接收到能量,并且接收功率不低于给定阈值。文献[12~13]将充电器部署在距离网络一定高度的平面上,通过对该平面进行网格化,确定充电器的最佳部署位置。不同的是,文献[12]只考虑节点能否被覆盖到,优化目标是确保每个节点都能被覆盖到,而文献[13]加入了对节点能量消耗率和接收率的考虑,优化目标是确保每个节点的能量接收率不小于消耗率。
本文的研究基于定向充电模型,在保证无线可充电传感器网络持续运行的情况下,最大化网络累计充电增益的充电小车优化调度问题。
1 网络模型与假设
1.1 传感器节点模型
在基于定向充电的传感器网络中随机抛洒传感器节点。传感器节点皆具有数据感应、数据生成和传输、能量接受的功能。网络中传感器节点可分为可充电节点和汇聚节点。可充电节点负责感应监控环境生成数据,通过多跳路由把感知的数据传递给汇聚节点。
环境感应、数据生成与传输是传感器节点的主要能耗方式。假设传感器节点数据对1 bit数据进行感应,传输和接收所需能量为ec,根据文献[14~ 15]有
(1)
其中,e0表示传感器用于数据感知、数据编码和调制的能耗;e1表示单位比特的能量损失系数;dr表示传感器之间的传送数据距离;α表示路径损耗系数(一般为2~4),本文假设各个节点获得信息速率相等。
1.2 充电小车模型
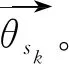
(2)
节点的能量接收功率可以基于Friis方程[16]计算
(3)
其中,Pr是能量接受功率;Pout是能量发射功率;L是路径耗损因子;GT是发射天线增益;GR是接收天线增益;λ是发射波的波长;η是整流器效率;β是用于调整自由方程的参数;d是发射与接收天线之间的距离。
1.3 网络模型
如图1所示,在L×L的区域中任意随机抛洒n个传感器节点S={s1,s2,…,sn}。网络中任意节点总容量为Emax,m辆移动充电小车集合为MC={mc1,mc2,…,mcm},集合中任意小车的总电量为Cmc,其输出功率为Pmc。静止基站b位于网络平面的中心位置。为确保网络持续运行,充电小车以T为周期对传感器节点进行周期性充能。
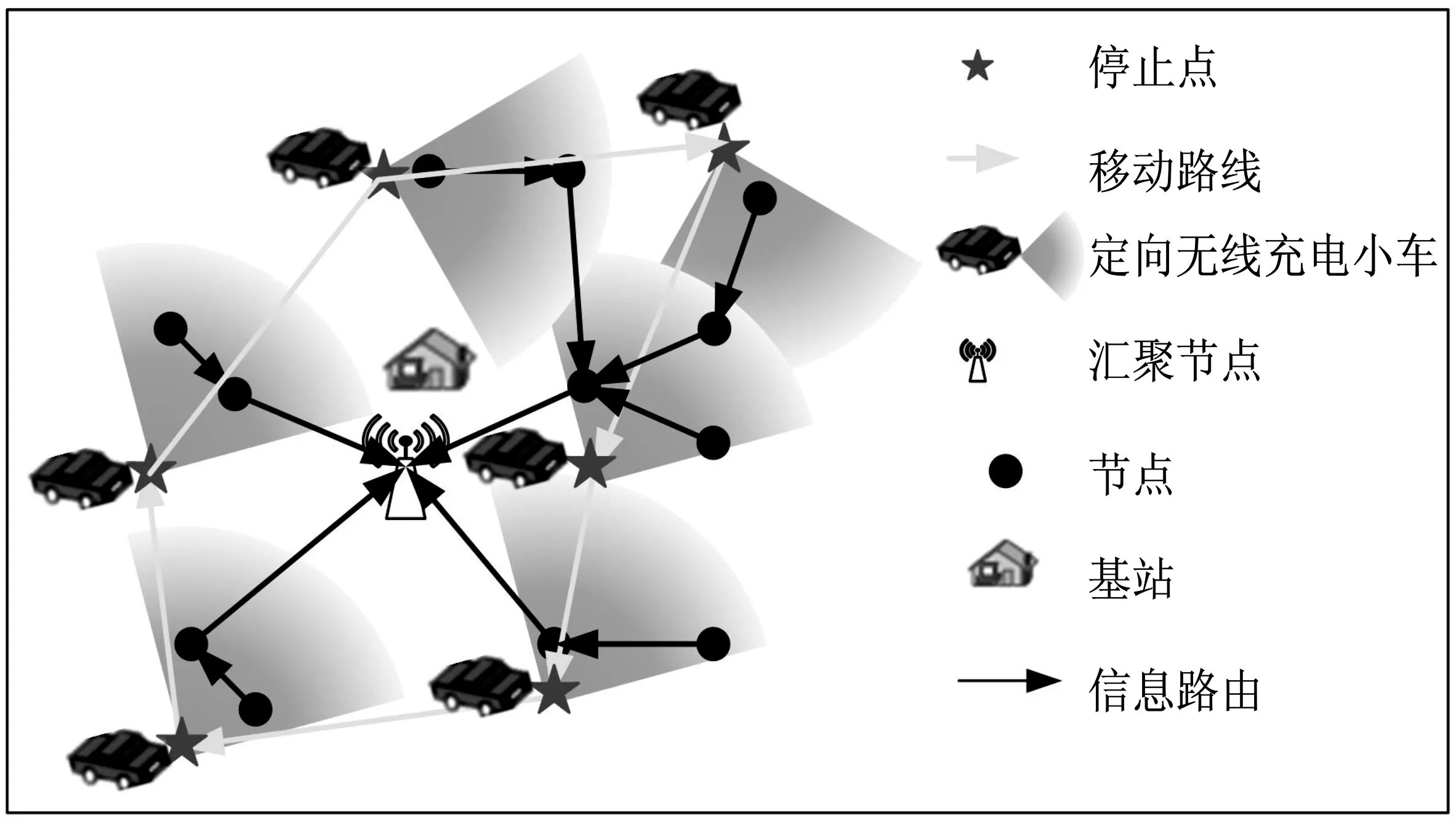
图1 定向充电传感器网络模型Figure 1. Directional charging wireless sensor network model
2 问题定义
无线传感器网络中等待充电感器节点集合为S={s1,s2,…,sn},传感器节点最高电量Emax记为Cv,剩余电量为Rv,集合中任意节点si∈S的能量接收速率为γi,能耗速率为pi。集合MC={mc1,mc2,…,mcm}为充电小车集合,集合中任意小车mci∈MC的总电量均为Cmc,其输出功率为Pmc,通过效用函数f(x)模拟传感器充能,候选停靠点集合A={a1,a2,…,an},候选停靠点aj∈A对应传感器节点si∈S的位置。b为基站给小车充能。每个候选停靠点aj∈A的包含的传感器节点记为Sai,给Sai充电需要消耗Τai的时间。
从基站b出发,充电小车mck∈MC中途停靠在aj∈A,对Sai中的传感器节点进行定向充电,充电周期为T,完成充能后返回基站b进行充电。在保证传感器网络持续运行的前提下,最大化网络累计充电增益。该问题形式化定义为
(4)
(5)
(6)
ηajyaj>δ,j∈S
(7)
yaj≤ua,j∈S
(8)
(9)
Tpizik=Taγizik,i∈Sa
(10)
Emax-(T-Ta)·pi≥Emin,i∈Sa
(11)
xijk,yia,zik∈{0,1},a∈A,k∈MC
(12)
3 近似算法
3.1 充电方向选择算法
充电方向选择是指在当前候选停靠点下选择充电小车的充电方向,具体过程是:首先充电小车以每个不同的节点为一个边界逆时针旋转;然后确定每个朝向覆盖到的节点集合并计算每个方向的覆盖效用,如图2所示。
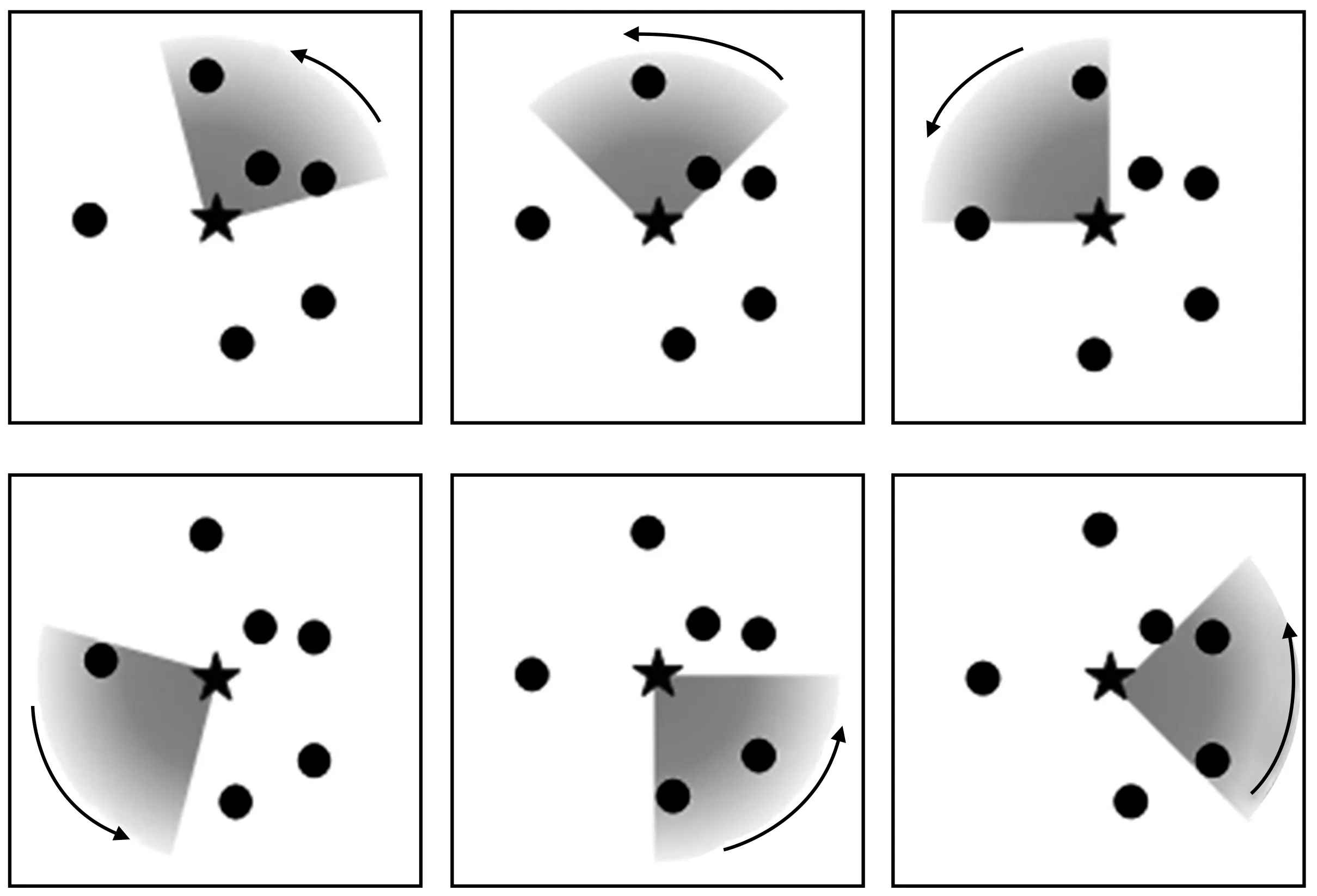
图2 定向充电方向选择过程Figure 2.Process of directional charging direction selection
伪代码如下:
算法1最大覆盖效用充电方向选择算法。
输入传感器集合O={o1,o2,…,oN};充电器位置(cx,cy);充电器的覆盖距离D;覆盖角度为A。
1.OCS=Ø,i=0;
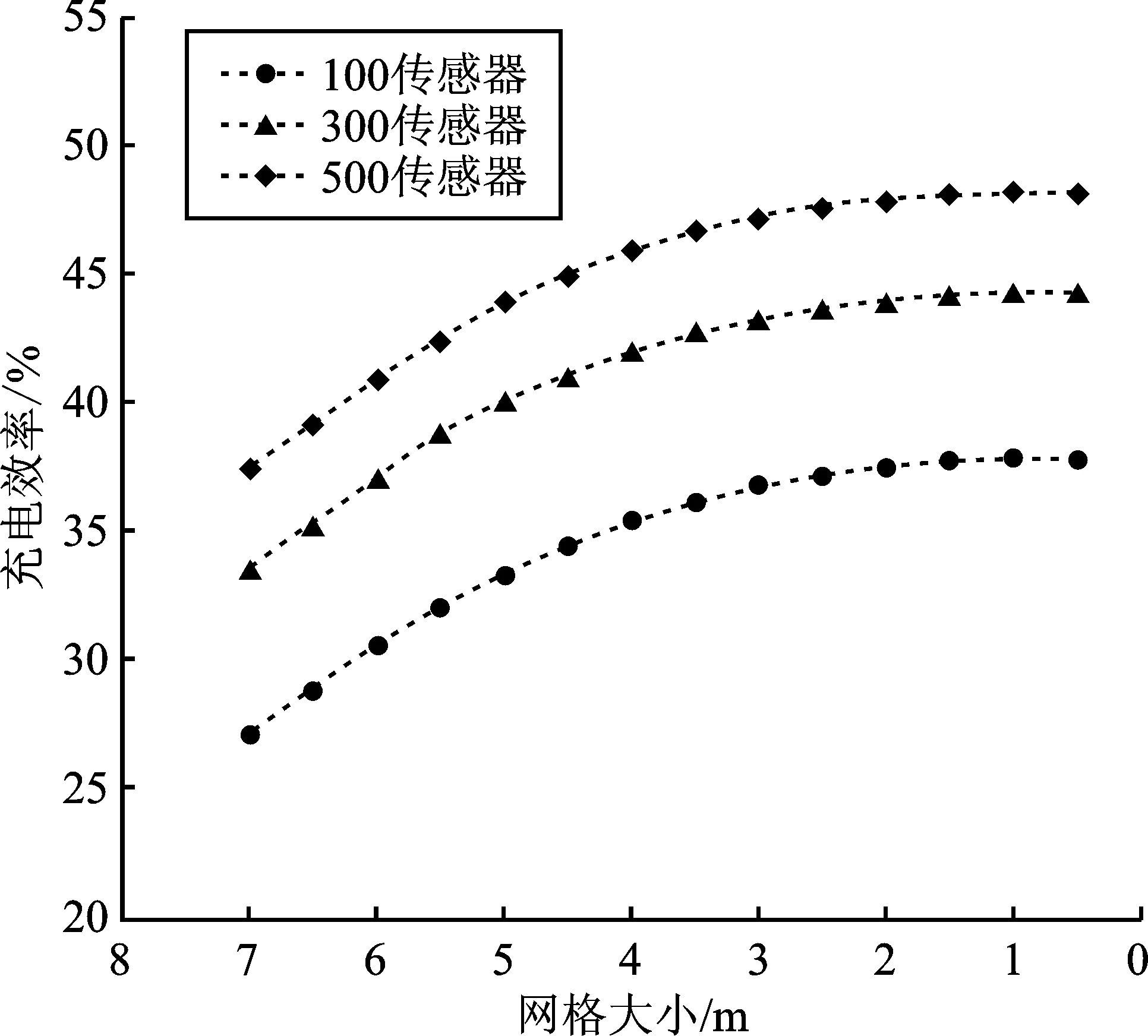
2.当i 3.计算传感器Oi与充电小车的欧几里得距离di,如果di 4.循环结束; 5.如果OCS=Ø,算法结束,否则继续第6步; 6.L=len(OCS); 7.计算集合OCS中的传感器与充电器位置形成的夹角集合θ={θ1,θ2,…,θL},并且将集合OCS中的传感器按照对应的夹角大小升序排序; 8. CU=∅,k=0,当i 9.把充电器覆盖扇形px的始边摆于OCS[k]; 10.将终边置于(θk+A)%360; 11. CU=CU∪{CUk},k=k+1; 12.循环结束。 输出MCU和Umax。 停靠点选择算法调用了方向选择算法,将二位传感网络划分为网格,以网格的顶点作为候选停靠点位置。充电小车每次停下来只选择一个方向进行充电,充电器的覆盖范围是一个半径为D的90°扇形,只有满足每个扇形可以对网络全覆盖的前提下才可能确保没有节点遗漏。 伪代码如下: 算法2最大化覆盖效用总和停靠点选择算法。 输入传感器集合O={o1,o2,…,oN}。包括每个节点的索引值和对应的坐标点;充电器的覆盖距离为D;覆盖角度为A。 1.对二维传感器网络进行格式化,以网络交点作为候选停靠点,获得充电器候选停止位置集合CS={cs1,cs2,…,csi,…,csn}; 2.令最终被选的停止位置集合FCS←Ø,令其对应的停止位置覆盖集合为Ns←Ø; 3.当O≠Ø并且CS≠Ø时; 4.AUmax=0,AMCU=Ø,csmax=Ø,i=0; 5.当i 6.调用方向选择算法,得到csi位置最大覆盖效用值Umax及其最大覆盖效用节点集合MCU; 7.若Umax>AUmax,则AUmax=Umax,AMCU=MCU,csmax=csi; 8.循环结束; 9.如果AUmax=0,循环结束,否则继续下一步; 10.FCS=FCS∪{csmax},Ns=Ns∪{AMCU},CS=CS-{csmax},O=O-{oi/oi∈AMCU} 11.循环结束。 输出FCS和Ns。 (1)Pj的能耗之和不大于充电小车的最大容量CMC,即 (13) (2)pj路径上总的消耗时间小于小车充电周期T,即 (14) (15) 伪代码如下: 算法3基于分解TSP的路径规划算法。 输入停靠点集合D,充电小车集合MC,在停靠点a处对节点j的充电效率ηaj,充电小车容量Cmc,服务基站b,充电周期T,TSP路径p=(b,Π1,Π2,…,Πn,b)。 1.当p≠Ø时; 4.获得第j条闭合回路用p=(b,Π1,Π2,…,Πn,b) 5.从TSP路径中去掉pj包含的停靠点,j←j+1; 6.结束循环。 输出充电小车mcj的充电路径pj。 分析计算网络对应所需充电小车的数量,首先要对单小车可服务网络规模进行分析计算。假设小车充电队列集合为p=(Π0,Π1,Π2,…,Πn,Π0),集合中Π0是基站位置,Π0i(1≤i≤n)是传感器si∈S所在位置。在充电队列p=(Π0,Π1,Π2,…,Πn,Π0)中任意相邻节点间最大距离为lmax。为了保证传感器网络的持久化运行,需要满足如下要求: (1)单位充电周期内,充电小车对节点充电的总电量不小于队列中节点消耗的总电量,即 (16) 其中,v是充电小车的移动速率;T是充电周期;pMC是充电小车充电功率;n是节点数量;c是节点的平均能耗速率,推导得 (17) (18) 因为pMC≥c,所以f′(t)≥0,即单个充电小车服务的节点数与充电周期时长正相关; (2)单位充电周期内,所有节点的剩余能量不低于节点正常工作的最低电量。假设节点的初始电量为满电量Emax,所以周期长度T有 (19) (20) 在100 m×100 m、200 m×200 m和300 m×300 m的区域中分别多次随机抛洒50、100、150、200、250、300、350、400、450、500个节点,从网格大小、网络规模、充电形式等因素来分析其对充电小车能量利用率与累计充电增益的影响。无线充电小车依照前文所述模型和算法对节点进行充电。 在100 m×100 m的区域中多次分别随机抛洒100、300、500个节点,改变网格大小,分析对充电小车充电效率的影响。 图3 网格大小对充电效率影响Figure 3. Effect of grid size of charging efficiency 图3显示了随着网格大小的减小,充电小车的充电能量利用率正在提高。当节点数量为100,网格大小由7 m减少到1 m时,充电小车的充电效率提高了近38%。当节点数为300,网格大小由7 m减小到1 m时,充电小车的充电效率提高了近27%。当节点数为500,网格大小由7 m减小到1 m时,充电小车的充电效率提高了近23%。由此可见,随着节点数的增加,充电效率的提升有所减缓,当前网络规模下网格大小为1 m时效果最佳。 图4 网络规模对于充电累计增益的影响Figure 4. Effect of the size of network on the charging efficiency 由图4可知,随着节点数量的增加充电小车的能量利用率在逐渐提高。由于节点的数量增加,因此充电小车每次能够覆盖到节点数增加,因此更多的能量被节点接收,能量利用率得到了提高。同时,在节点数量不变区域变大时,充电小车的能量利用率在降低,因为节间的距离变大,充电小车消耗在路上的能量增多,导致充电小车能量利用率降低。 图5 节点数量对于充电累计增益的影响Figure 5. Effect of the number of nodes on the cumulative charging utility 图5显示了在100 m×100 m的区域不同节点数量对于网络累计充电增益的影响。在相同节点数量下,定向充电的网络累计充电增益高于全向充电,且随着节点数量的增加同种充电方式的网络累计充电增益在增加,在200~250个节点的情况下效果尤为显著。而当节点数大于250个以后,全向充电的增幅低于定向充电,说明此时全向充电的充能利用率不如无线充电。 本文研究了基于定向充电模型,在保证无线可充电传感器网络持久运行的情况下,最大化网络累计充电增益的优化调度问题。针对该问题,本文提出了近似算法。近似算法包括3个部分:(1)基于最大化覆盖效用的方向选择算法;(2)基于方向选择的最大化覆盖累计效用的停靠点选择算法;(3)基于TSP的路径规划算法为充电小车规划移动路径。通过仿真实验对比不同的充电策略。实验结果显示,相比全向充电,本文提出的充电策略可以明显提升网络的累积充电增益。定向充电模型是无线可充电传感器网络无线充电领域中新兴的模型,基于定向充电模型还有很多新的研究方向,例如如何延长网络生命周期等。3.2 停靠点选择算法
3.3 路径规划算法
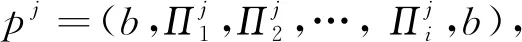
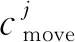
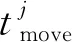
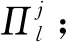
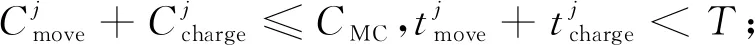
4 网络规模分析
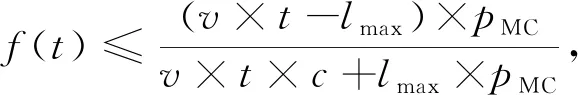
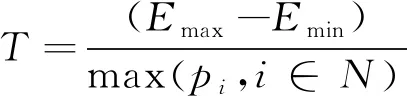
5 模拟实验
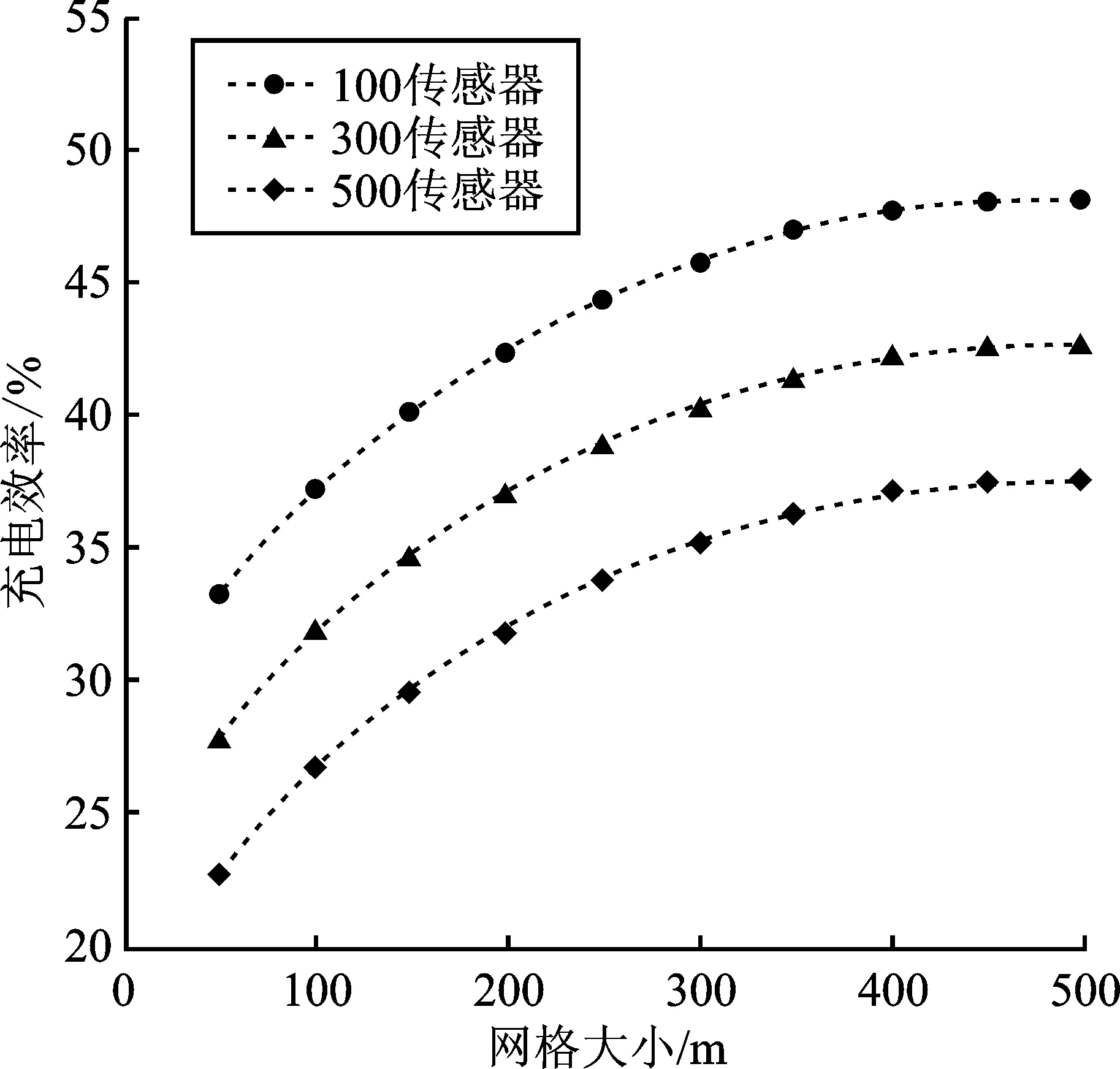
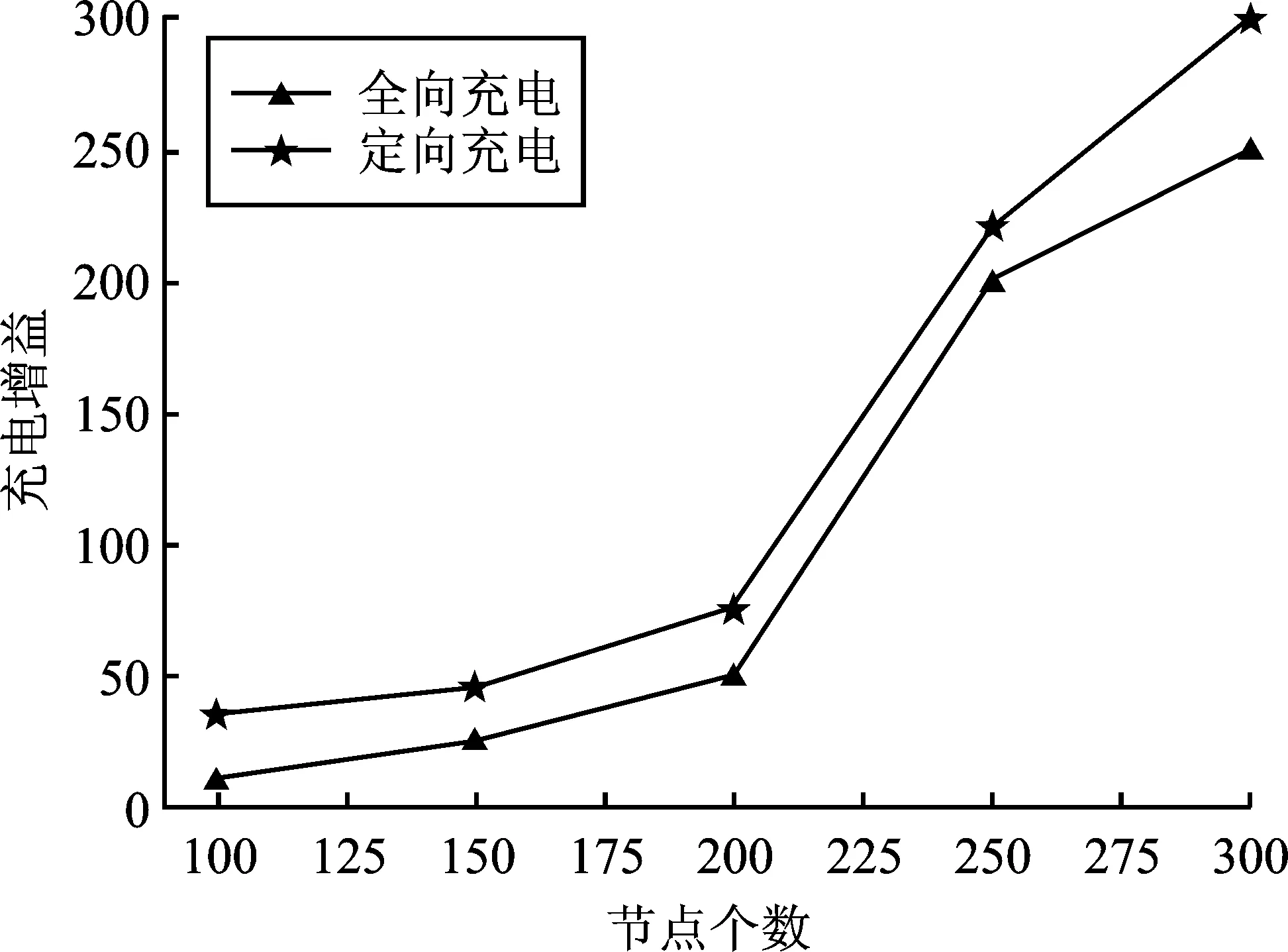
6 结束语
